街道密度抑或空间关联影响城市空间分区

杨 滔

1 问 题

近年，小街坊、密路网的倡议提出来之后，较高密度的街道路网又再次被视为是城市具有活力的重要因素之一。过去不少研究认为，较小的街坊块以及较密的街道网络都是现代工业化城市所缺乏的要素，使得那些城市缺少诸如历史老城那样丰富多彩的街头生活气息。简·雅各布斯（Jane Jacobs）就是其中典型的代表之一[1]。美国新城市主义之中，较高的街道密度也是其重要的判断指标之一。不过，不少学者也指出，不少新城市主义的城镇并未形成生机勃勃的氛围，反而往往空无一人[2]。此外，威廉·怀特（William Whyte）对纽约进行长期的录像观测，发现街道活力较高的场所也许未必出现于小街坊之中，有可能出现在狭长的广场之中、阳光充沛的嘈杂马路边、座椅合适的街头等，并提出每个场所与其他场所的连通性至关重要[3]。比尔·希列尔研究低收入住宅中的社会和空间现象之后，也提出相对于局部单纯加密路网的举措，空间之间的整体性联系才是为城市带来经济活力的主要动力[4]；并明确了局部街道加密只是提升了局部的可达性，而整体可达性则是把城市各个部分聚集在一起的机制[5]。另一方面，城市的活力也看似来自其多样性，不同的城市分区具有不同的特征，那么这些城市分区与街道网络的密度有关系吗？这也带来一个问题，城市看似具有某种秩序，同时又具有貌似混乱的多元性，那么城市空间是如何平衡这种秩序和多样性的？本文将从空间流动的角度，关注城市分区秩序的空间规律，并探索可能的理论发展方向。

我们先来大致看看北京和伦敦历史中心区以及伦敦道克兰区的空间情形。显然，北京和伦敦的历史中心区都发展得相对成熟；而伦敦道克兰区的城市更新始于20世纪80年代，其中包括大量彼此独立的住宅小区或商务区，反映了现当代城市发展的理念之一。我们采用两个交叉口之间的线段长度去类比街道路网的密度。可发现，伦敦道克兰区的线段长度最短，平均为41.6m；伦敦中心区其次，平均为44.4m；北京中心区最长，平均为69.8m。这其实反映了当代高密度建设的社区或小区，或多或少受到了美国新城市主义或英国新乡村主义的影响，其开发的街道密度并不低，甚至要高于传统的历史城区。此外，这也体现了北京街坊规模或院落尺寸比伦敦的要大些，然而这并不暗示北京的街道活力就要低些。伦敦道克兰区的街道活力反而明显低于伦敦中心区和北京中心区，而其街道路网的平均密度反而最高。我们再看一下轴线长度，也就是视线或运动趋势所限定的最长的线，且以最小的数量遍及整个研究城区。我们较为诧异地发现：伦敦道克兰区的轴线平均最短，为140.9m；北京的其次，为247.4m；伦敦的最长，为253.4m。由于北京是明显的方格网结构，而伦敦是更为自由的结构，所以直觉上会认为北京应该具有平均最长的轴线。北京的轴线并不像设想得那么长，这是由于北京的胡同空间基于较为封闭里坊发展而来，且当地的封闭小区或大院也不少，从而导致了北京的轴线在局部层面上较为细碎。

对于道克兰区，很明显由于其轴线被封闭小区、高档办公区等打断，形成了不少孤立的“岛屿”，并未形成如同老城区那样连绵细致的街道网络。因此，道克兰区反而并未在更大尺度上通过较长的视线轴线将各个片区有机地联系起来，这看似对其活力有一定影响。在很大程度上，这说明了城市的活力很可能并不是完全源于街道空间的平均密度，反而是源于城市在较大尺度上的彼此联系。

图1 / Figure 1三个案例的街道密度图Street Density Map of The Three Cases

图2 / Figure 2三个案例的拼贴分区图案The Periodic Patchwork Patterns of The Three Cases

我们再看看街道网络密度。以1,200m范围内街道线段的数量近似地度量街道网络密度（图1），可发现：伦敦高密度的街道网络集中在历史老城区，如老金融中心（The City）、西区以及泰晤士河南岸的一小部分，呈现出明显的单中心结构；北京高密度的街道网络围绕在故宫中心，南北向更为强烈，也大致呈现出单中心结构，只不过体现为一个高密度的环，环所围绕的是相对低密度的故宫；伦敦道克兰区西面靠近老金融中心（The City）的部分有较高的密度，然后向东面逐步降低街道网络密度，只是在新金融城（Canary Wharf）和贝克顿（Beckton）密度有所提高，总体为从西到东逐步降低的趋势。然而，如果采用平均米制深度（Metric Mean Depth）或嵌入度，在上述3个案例之中都会发现分区的现象（图2），称为拼贴图案模式（Patchwork Pattern），貌似与某些地名所确定的分区类似。这说明街道密度本身并不会推动分区现象的产生。于是，我们需要去探索这些分区是何种几何机制导致的。

2 城市分区的“波峰与波谷”模式

过去的研究表明：由平均米制深度生成的分区模式可以转化为“波峰与波谷”模式，这种转化采用山形散点图，即纵轴为特定半径k的平均米制深度的倒数，横轴为半径n的平均米制深度。这为我们提供了一种方法，用于探索任何地区特定半径下的米制特征与整个网络的米制整合模式之间的关系。该方法应用于伦敦和北京的历史中心地区以及伦敦道克兰区。

在两个历史地区，可发现所有由地名所界定的地区在特定半径下的山形散点图中呈现为波峰或波谷（图3）。例如，当半径为1,600m时，伦敦历史中心地区的老金融城（The City）呈现出明显的波峰，其顶端是伦敦皇家交易所和英格兰银行等，这里是米制整合度最大的地方，而其周边则呈现出绿色和蓝色的格网，表示空间相对隔离；而布鲁姆斯伯里（Bloomsbury）则呈现出相反的情景，体现为波谷，其谷底是伦敦大学学院的神经学院和英国国家神经医学院，该地区在历史上就属于伦敦的大学校园区，其米制整合度最低，而它们周边的地区具有更高的米制整合度。又如半径为1,100m时，北京历史中心地区的东四地区呈现出波峰，其顶端是铁营胡同，明朝属思诚坊，又名铁箭营，清朝称铁匠营，多有铁匠作坊，打马掌、制冷兵器，其米制整合度最大，周边则米制整合度较小；而南锣鼓巷呈现出波谷，其谷底是东棉花胡同，中央戏剧学院就在旁边，其米制整合度最小。大致而言，与商业有关地区往往会呈现出波峰模式，而与大型公共机构或封闭住宅有关的地区常常呈现出波谷模式。

不过，在伦敦道克兰区案例之中，某些地名地区呈现出波峰或波谷，而某些地名地区则呈现出多个波峰或波谷，并不能在较高的半径下融合成为一个波峰或波谷（图4）。例如，皇家码头（Royal Docks）地区在1,700m下呈现出两个波峰，一个为银城（Silvertown），另一个为皇家码头机场南部的住宅区，在任何半径下它们都不能整合为一个统一的波峰或波谷。对于银城，在400m、500m、700m、1,200m处都反复地呈现出波峰。与上述历史中心区相比较，说明伦敦道克兰区由于其各个地区、社区、小区彼此之间相对独立，常常被绿化或水道隔离，并未形成肌理上彼此交织的细致网络，所以各个地名地区并未融入其周边地区，它们之间的空间非连续性随度量半径的增加，而被反复地识别出现，体现为不同半径下的波峰或波谷。

图3 / Figure 3伦敦和北京历史中心区的波峰和波谷模式The Peak and Trough Patterns of The Historic Central Districts of London and Beijing

图4 / Figure 4伦敦道克兰区的皇家码头的波峰和波谷模式图The Peak and Trough Patterns of The Royal Dock of London Docklands

3 拼贴图案模式与街道密度变化

不管伦敦和北京的历史中心地区，还是伦敦道克兰区，在不同的半径下其空间网络都呈现出拼贴图案模式。要么是暖色的分区图案，对应于波峰；要么是冷色的分区图案，对应于波谷。这种波峰或波谷的模式貌似与希利尔（Hillier）的网格强化理论有关，其理论认为城市的增长导致了中心区的街坊块变小，而周边的街坊块则保持较大的规模，从而使得城市网络中从所有街道到其他街道之间的米制距离之和最优。那么，我们对每个暖色图案（波峰）或冷色图案（波谷）进行研究，比较构成分区图案的所有线段的特征以及那些参与到形成分区图案的所有线段的特征，后者包含在特定半径下形成的分区图案的所有线段在同样特定半径距离下连接到周边的线段，因为这些周边线段都参与到特定半径下米制平均距离的计算之中。换言之，我们期望比较每个分区图案与其周边的关系。

图5显示了1,400m半径下伦敦三片暖色分区图案和三片冷色分区图案。前者大致分为老金融区（The City）、克勒肯维尔（Clerkenwell，即艺术和科技创意活动的聚集区）、苏荷（Soho）与考文特花园（Covent Garden）等构成的市中心活跃地区；后者大约分为布鲁姆斯伯里（Bloomsbury，即伦敦的一些大学所在地）、梅费尔（Mayfair）的一部分（即西区的高档办公住宅区）、威斯敏斯特（Westminster）。其中黑色部分为由1,400m半径下米制平均距离所生成的分区图案，灰色部分为分区图案1,400m范围内的周边地区。

从视觉上，很难一下区分黑色部分和灰色部分的街道密度。然而，定量的分析（表1）表明：对于暖色分区图案而言，黑色部分的平均街道长度小于灰色部分，且黑色与灰色的比例均值为0.74，差别较为明显；而对于冷色分区图案而言，灰色部分的平价街道长度小于黑色部分的，且黑色与灰色的比例均值为1.40，差异较为显著。对伦敦其他的分区图案进行同样的分析，得到同样的结论。 这说明伦敦的暖色分区街道密度比其周边的更高，而冷色分区的街道密度比其周边的更低。

对于北京1,400m半径下的分区图案和伦敦道克兰区1,200m半径下的分区图案进行分析，也可得到完全相同的结论。表2将3个案例中所有分区图案的街道长度平均值进行了进一步分析，还比较了它们的平均连接度，即每条街道段连接其他街道的数量。这两个变量都反映了街道的密度。对于暖色分区而言，黑色部分的街道长度均值要明显小于周边灰色部分，而黑色部分的连接度均值只是稍微高于周边灰色部分，这说明暖色分区的街坊块大小要明显小于周边灰色部分。对于冷色分区而言，黑色部分的街道长度均值也显著地大于周边灰色部分，而黑色部分的连接度均值也只是些许低于周边灰色部分，这表明了冷色分区的街坊块大小要明显大于周边灰色部分。

除了上述的普遍性规律之外，还可发现虽然伦敦道克兰区的暖色或冷色的分区图案的街道平均长度都小于伦敦和北京中心区，然而伦敦道克兰区冷色分区图案的街道平均连接度明显小于伦敦和北京中心区。在一定程度上，这反映了伦敦道克兰区冷色分区作为暖色分区的空间分隔，其空间非连续性尤为明显，即各个分区之间的联系性较弱。

不过，这3个案例都反映出暖色分区图案与冷色分区图案彼此相邻，构成了周期性相间的结构（Periodic Structure）。这实际上暗示了街道密度更大的分区与街道密度更小的分区彼此相邻出现，而对于每个分区又存在更为精巧的空间结构布局差异。波峰与波谷的模式也体现了这种周期性特征。暖色分区对应于波峰，即分区中存在米制整合度最高的中心，对应于峰顶，也就是街坊块较小的部分，而其周边地区的街坊块较大，这称之为“中心—边缘”母题；冷色分区对应于波谷，即分区中存在米制整合度最低的“边缘”，对应于谷底，也就是街坊块较大的部分，而其周边地区的街坊块较小，这称之为“边缘—中心”母题。因此，我们假设周期性相间的结构来自于非均匀街道密度的变化，即街道密度的变化才是城市分区的内在空间形态机制。

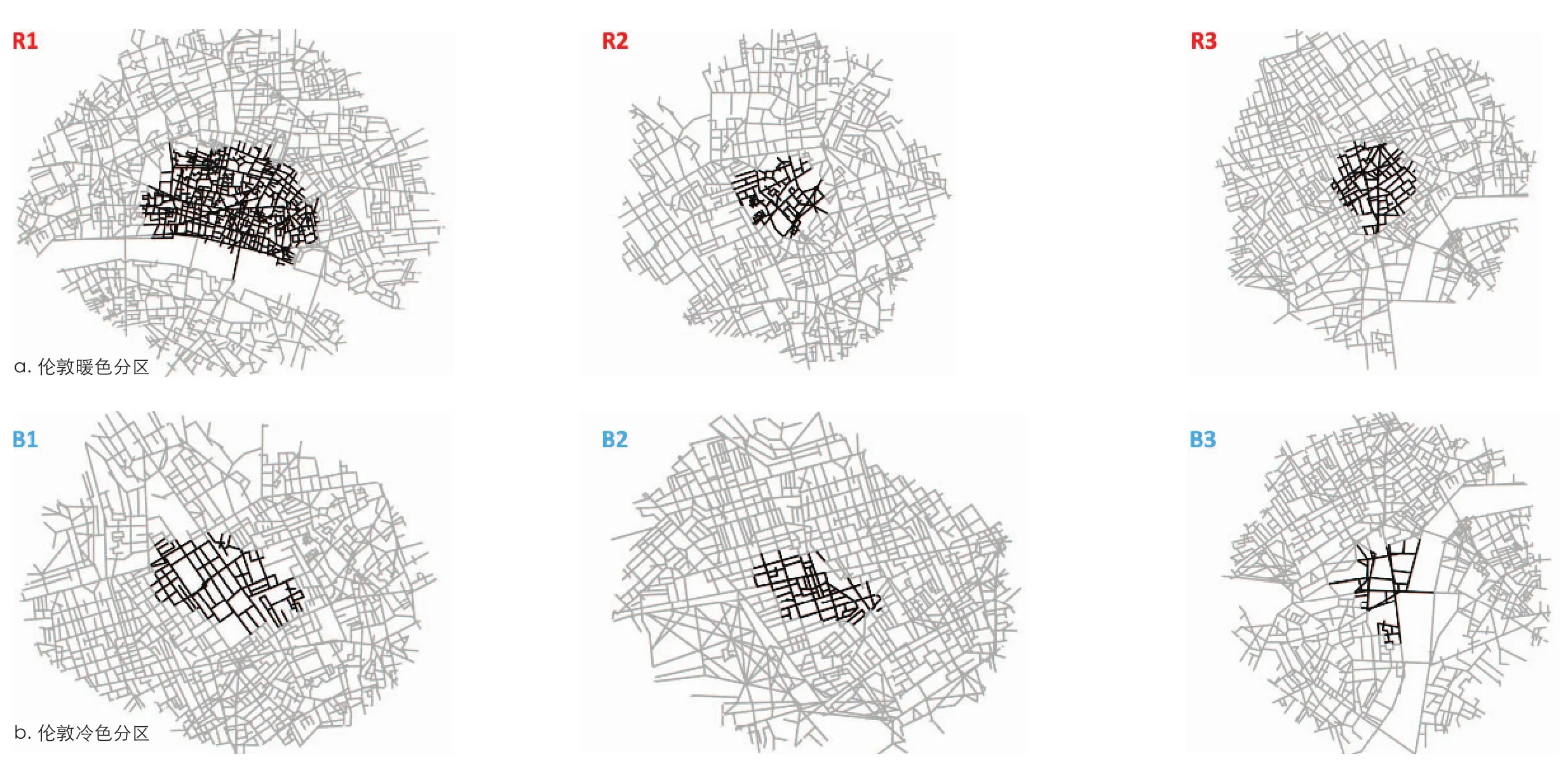
图5 / Figure 5伦敦拼贴分区图案 （黑色表示分区；灰色表示参与分区形成的周边地区）The Patchwork Patterns of London (Black denotes Patches, Grey means the surrounding areas involved in the formation of the patchwork patterns)

4 两个母题与局部几何变化

基于米制平均距离而生成的拼贴分区图案，不管是暖色的，还是冷色的，都有位于城市中心区的，也有位于城市边缘的。然而，城市中心与边缘的街道密度肯定不一样，那么为什么那些拼贴分区图案都具有类似的米制平均距离？在此，我们采用概念性的案例加以研究。图6展示了两个“中心—边缘”母题，而其密度明显不一样。第一个代表位于城市边缘地区的“中心—边缘”母题，第二个代表位于城市中心地区的“中心—边缘”母题。对于图中带黑点那条线段，前者的米制嵌入度（即街道随尺度变化的速率）为1.56以及其米制平均距离为9.03；而后者的米制嵌入度则为1.59以及其米制平均距离为9.07。两者的数值非常接近，都反映出“中心—边缘”母题中街坊块的大小从中心向边缘逐步变小的趋势。这说明了暖色拼贴分区图案的出现在于街坊块在局部层面上由中心向边缘逐步变小的速率。

此外，图6还显示了两个“边缘—中心”母题，而其密度也明显不一样。同样，第一个代表位于城市边缘地区，第二个代表位于城市中心地区。对于图中带黑点的那条线段，前者的米制嵌入度（即街道随尺度变化的速率）为2.14以及其米制平均距离为10.1；而后者的米制嵌入度则为2.15以及其米制平均距离为10.0。两者的数值非常接近，都反映出“边缘—中心”母题中街坊块的大小从中心向边缘逐步变大的趋势。也就是说，不管城市中心区，还是城市边缘区，冷色拼贴分区图案的出现都源于局部层面上街坊块从中心到边缘逐步增大的空间机制。

普遍而言，上述分析体现了一种几何布局方式，从每个街坊块的角度来看，其周边的街坊块大小都随距离该街坊块的远近而发生变化。对于整个城市空间网络而言，其街道密度并不是匀质的；不同的分区具有不同的街道密度的变化速率，并导致了分区本身的形成。更为精确地说，几何布局的概念包括两方面的因素，即街道密度与半径变化率。对于空间句法的线段图而言，街道密度就是特定单位半径之内的线段数量。这实际上反映了静态的街道加密几何特征，即街坊块本身的大小特征。而半径本身可视为一种工具，选择距离某个原点线段的特定半径范围内的线段总量，可视为一种覆盖区域（Catchment Area）。于是，半径的变化速率可认为是一种覆盖区域的变化程度，同时也暗示了从特定街道去看待或感知周边覆盖区域的变化程度，称为局部几何动态变化。换言之，伴随认知半径的变化，一系列从特定街道去认知周边的覆盖区域内街道密度或街坊块大小的变化，构成了局部的几何动态变化特征，其中动态的街道密度变化速率貌似导致了拼贴分区的形成。

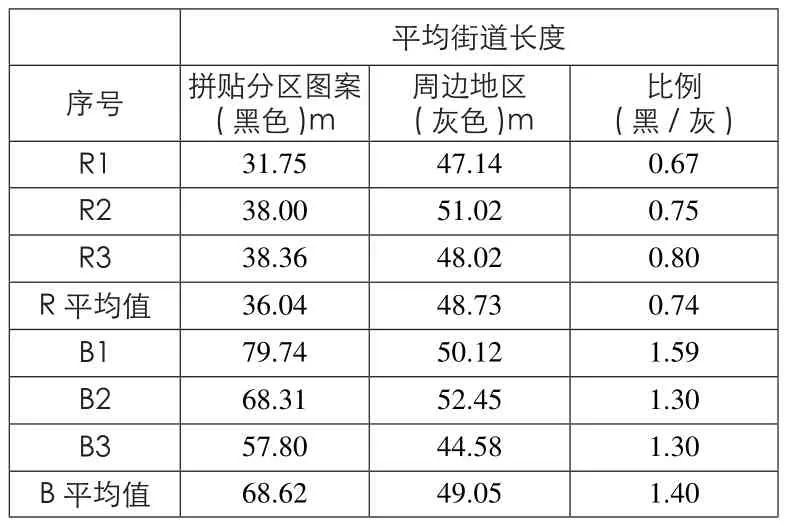
表1 / Table 1伦敦拼贴分区及其周边的街道线段长度A comparison of Street Length of The Patches and Their Surroundings in London

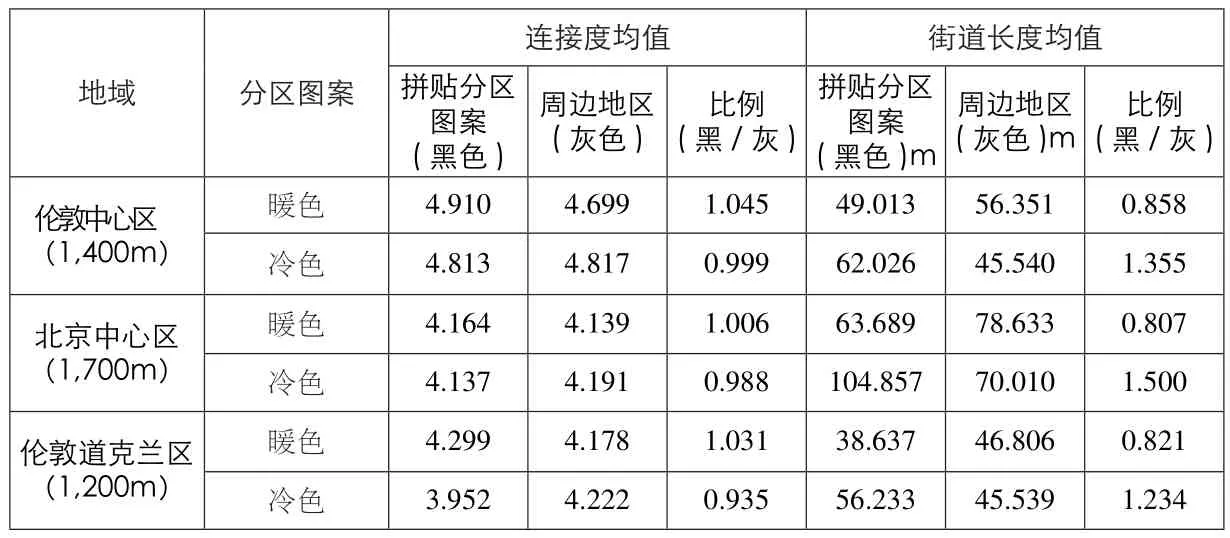
表2 / Table 2三个案例中暖冷拼贴分区及其周边的街道线段长度和街道连接度Street Segment Length and Street Connectivity of The Warm and Cold Coloured Patches in the Three Cases

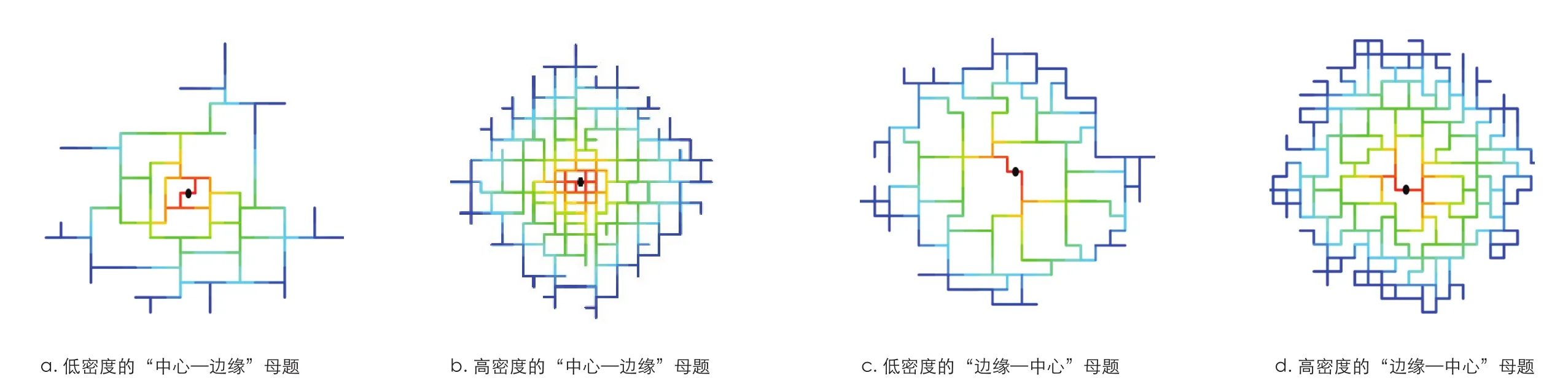
图6 / Figure 6不同密度下概念性的两个母题试验The Conceptual Test of Two Motifs in the differently intensified context

5 街道密度变化率与空间维度

街道密度可由较小半径下的街道线段数量（简称NC Rk）来近似模拟，那么我们分析不同冷暖拼贴分区内单独线段的NC Rk随半径变化的速率。例如，在伦敦历史中心区案例之中，我们选择半径为1,400m的拼贴分区图案，从红色、橙色以及蓝色的分区中分别随机地选择出3条线段。这些线段嵌入其周边地区的轨迹可由NC Rk与半径之间的散点图来表达。图7显示来自红色分区中的轨迹更直，而来自蓝色分区中的轨迹更为弯曲。非线性的拟合分析表明这些轨迹都符合幂指数曲线，可以表达为NCk=H×ka，其中NCk代表街道线段数量，H代表规模参数，α代表指数参数，k代表半径。

表3展示红色、橙色、蓝色分区中线段的米制平均距离、街道线段数量、规模参数以及指数参数。显然，同一类色彩分区中的米制平均距离和指数参数基本接近，而街道线段数量和规模参数差异较大。例如，线段610来自老金融城（The City），而线段19,191来自皮米里科（Pimlico），后者为相对远离市中心区的住宅区。前者的街道线段数量是后者2.7倍，而两者的指数参数（或米制平均距离）则几乎相同。由于1,400m并不大，那么1,400m以内的街道线段数量也代表了这两个区的街道密度。从而，这表明了同一类色彩分区（如老金融区和皮米里科）的街道数量或其密度本身有可能差异较大，然而代表街道密度变化率的指数则保持相对稳定。

实际上，从统计学意义上，我们确认了从半径400m到1,400m之间，95%的伦敦街道的NC Rk与半径之间存在幂指数关系，其R2为0.9。同时，也发现幂指数参数与米制平均距离之间也存在较强的相关性，其R2为0.813。这充分地说明了拼贴分区图案的出现来自于街道密度变化率。此外，所有的暖色分区内的线段具有小于2的幂指数，而所有冷色分区内的具有大于2的幂指数。从理论上来说，完全匀质分布的网格的幂指数接近2 ，实际上就代表了2维的平面空间。当幂指数小于2时，表明随半径增长，暖色分区的米制整合中心的街坊块遇到越来越多的较大街坊块，即“中心—边缘”母题；而当幂指数大于2时，表明随半径增长，冷色分区的米制整合中心的街坊块遇到越来越多的较小街坊块，即“边缘—中心”母题。这说明了两个母题本质上代表着城市网络的维度变形（Dimensional Distortion of Urban Grid），其细致的变化代表了城市空间网络的复杂性。

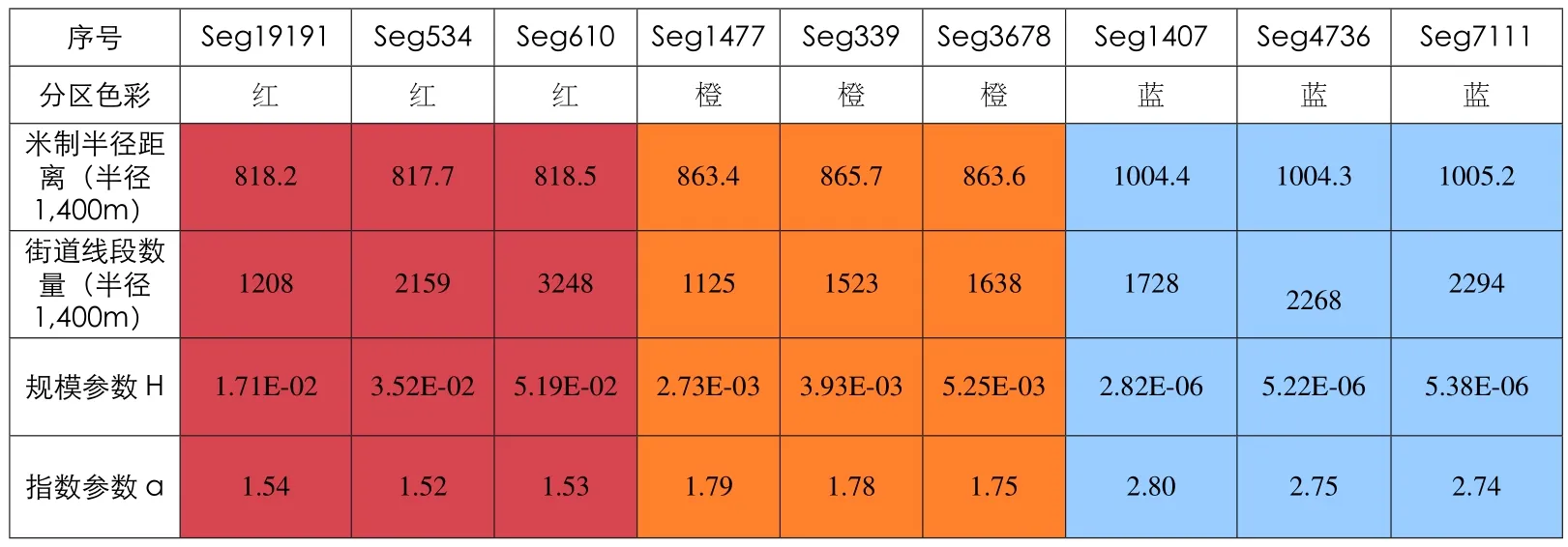
表3 / Table 3个体街道线段的米制平均距离、街道线段数量、规模参数以及指数参数Metric Mean Depth, Number of Segments, Scale Parameter and Exponent Parameter for Individual Street Segments

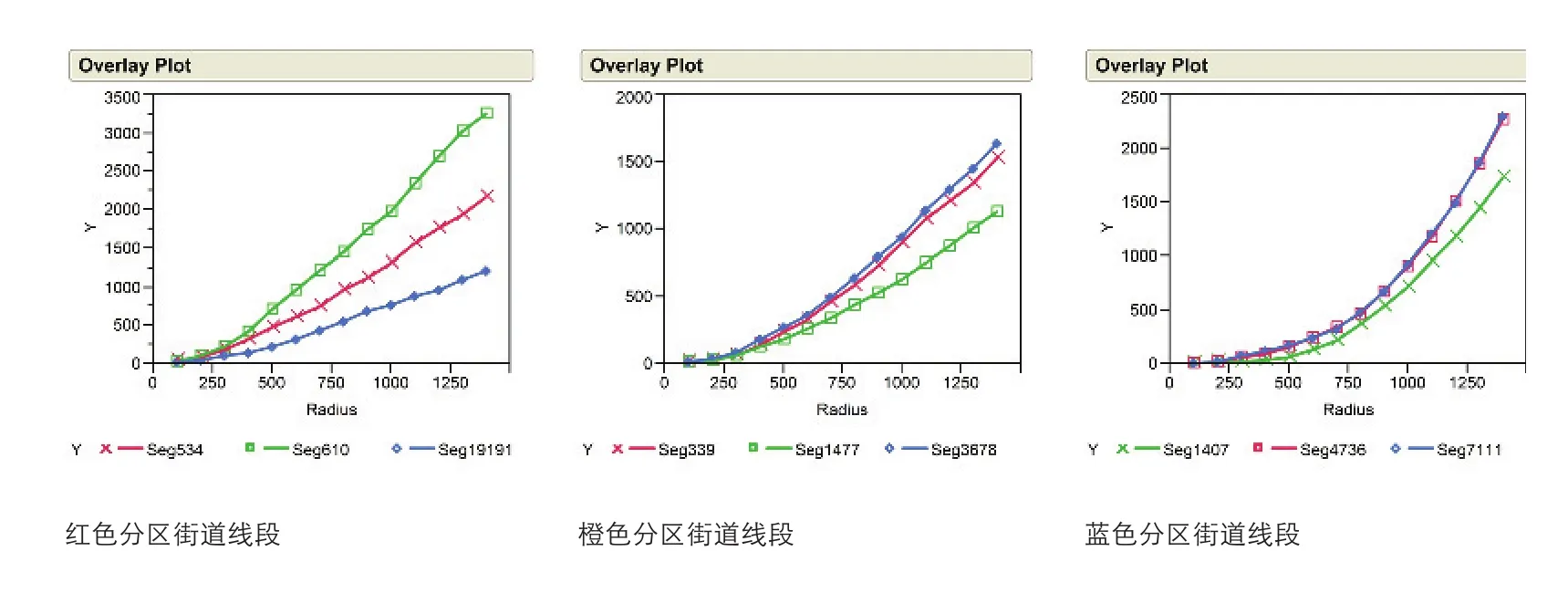
图7 / Figure 7个体线段融入周边地区的轨迹The Trajectory of The Embeddedness of Individual Segments

6 多尺度的网络加密

那么，为什么城市空间网络不是匀质的？这是否存在几何上的机制因素？我们开展一个概念性的试验。图8是700m× 700m的方格网，每个单元的一侧有10根1m长的线段组成。该方格网称之为Grid A，其中心还有一个300m×300m次级方格网，由红线标示出来，称之为SGrid A。一方面，对300m×300m次级方格网的中心区进行加密，然而保持总体的线段数目不变，那么SGrid B的中心加密程度最大，SGrid B1的次之，而SGrid B2的最小。它们共同构成了“中心—边缘”母题。另一方面，对300m×300m次级方格网的边缘区进行加密，然而保持总体的线段数目不变，那么SGrid C的边缘加密程度最大，SGrid C1次之，而SGrid C2最小。 它们共同构成了“边缘—中心”母题。

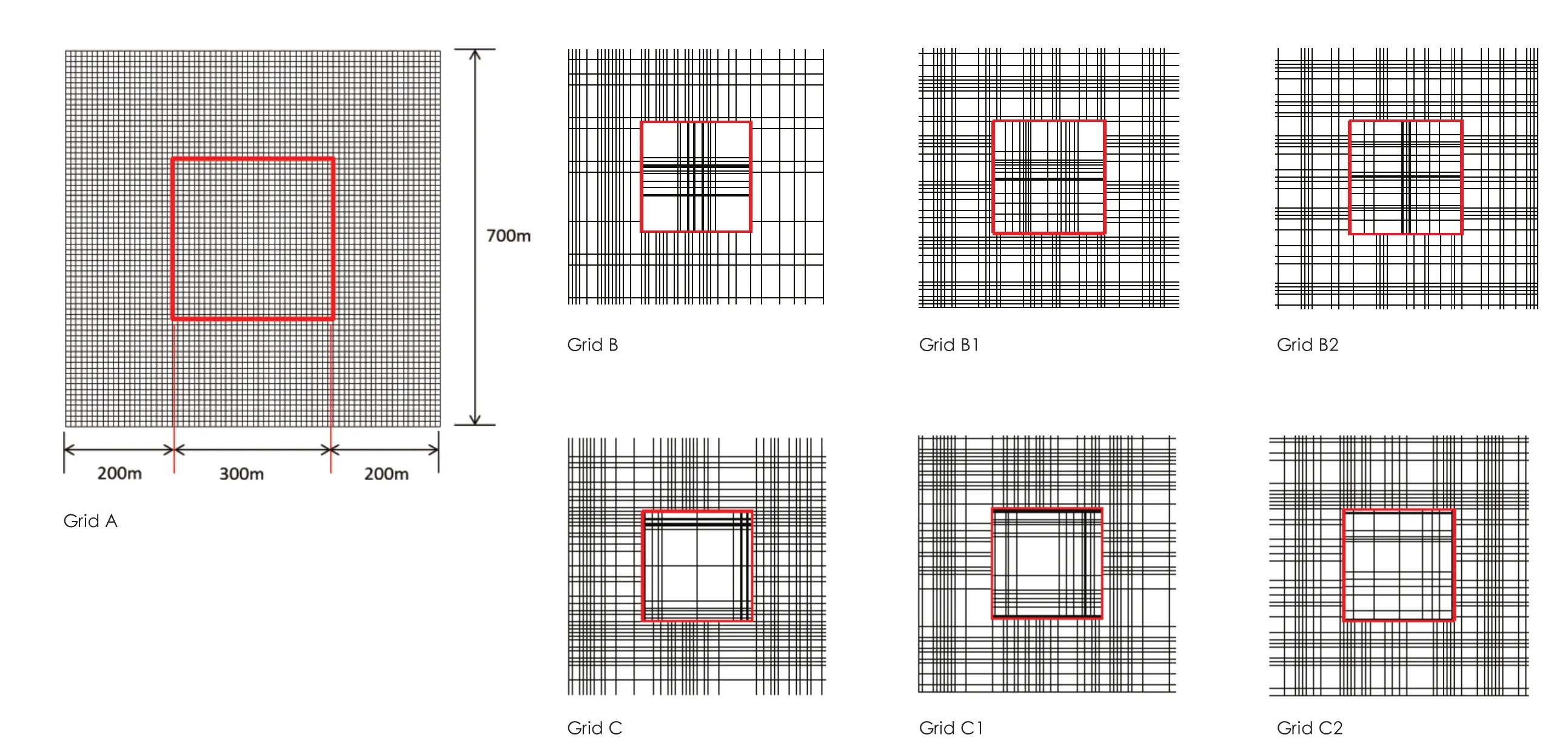
图8 / Figure 8伦敦道克兰区的皇家码头的波峰和波谷模式图A Test for Different Notional Grids

表4显示了所有300m×300m次级方格网的米制平均距离（MMD），半径从20m到200m，彼此间隔20m，最后的半径为n，即无限半径。其中红色表示MMD的数值大，也就是米制整合度低。显然，匀质的网络中300m×300m次级方格网并不具备最为整合的特征。从20m到40m，SGrids C和B（分别代表了“边缘—中心”母题和“中心—边缘”母题）最为整合；从60m到80m, SGrids C2和B2最为整合，而Grids B反而最为隔离；从100m到160m，SGrid C2（某种“边缘—中心”母题）居然最为整合；从180m到200m直到n，SGrid B最为整合。这说明两个问题。第一，匀质方格网的中央部分转变为“边缘—中心”母题或“中心—边缘”母题，在中小半径下米制平均距离将会变小，也就是变得在米制上更为整合。第二，作为“边缘—中心”母题的次级中心网络在较小和中等半径下，都具有较好的整合度，而作为“中心—边缘”母题的则在较小和较大半径下，都具有较高的整合度。这也暗示了非均质的网络具有较高的整合度。

表5显示了所有700m×700m整体方格网的米制平均距离（MMD），半径从20m到200m，彼此间隔20m，最后的半径为n，即无限半径。从20m到40m，Grids B和C更为整合；从60m到100m，Grids B2和C2更为整合；从100m到140m，Grids B1 和C1 更为整合；从160m到200m，直到n， Grid B更为整合。这说明：在半径小于140m时，随着中心次级网络的加密，不管是其中心抑或其边缘加密，整体网络的米制平均距离将会变小；而半径大于140m时，显然“中心—边缘”的母题将有助于使整体网络变得更为整合。这表明次级网络在其中心或其边缘的加密，都将使整体网络变得在米制距离上更为整合。

从理论上看，整个城市采用“中心—边缘”母题，将会使得整个城市层面上的米制平均距离最小;而在中小尺度之上，局部层面上的 “中心—边缘”母题或“边缘—中心”母题相互伴随出现，也将使得米制平均距离降低。因此，本文认为：城市存在不同尺度的网络加密，这结合了整体层面上的“中心—边缘”母题以及中小尺度上周期性交替出现且彼此依赖的两种母题，从而使得城市同时在不同尺度上去优化米制空间整合程度，推动不同尺度上的街道之间的彼此可达性或可渗透性，使得城市的几何布局满足不同尺度的多样化功能需求。在此意义上，周期性出现的拼贴分区图案来自于一种非整体性（或中微观层面上）的几何变化机制。

表4 / Table 4不同的300m×300m次级方格网的米制平均距离（MMD）Metric Mean Depth of 300m×300m Subgrids

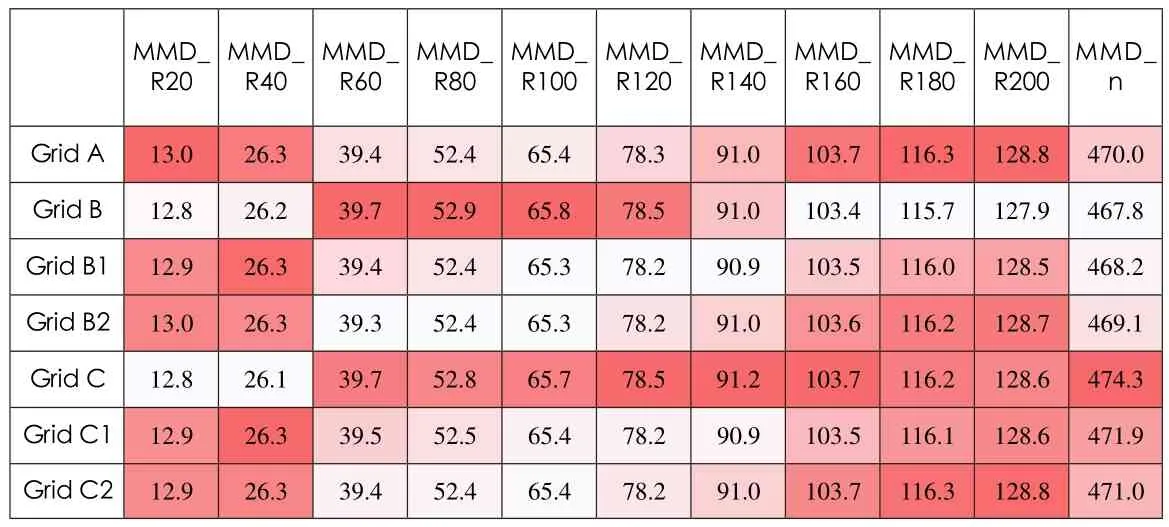
表5 / Table 5不同的700m×700m整体方格网的米制平均距离（MMD）Metric Mean Depth of 700m×700m Grids

7 讨 论

基于上述概念性试验的讨论以及相关的实证性研究，本文认为：城市不应该被视为一组街道密度不同且边界明确的组团或社区构成的空间网络，同时也不宜被类比为一组细胞构成的机体；应该将城市视为连续性的整体空间网络，其中不同部分的街道密度随尺度的变化而变化，从而优化所有尺度下街道之间的可达性。在这种意义上，不同尺度下所有街道空间的最优连接程度使得城市不再是匀质网络，从而体现为街道密度随尺度的变化（或我们感知城市的范围变化）而不断地变化，可类比为多维网络的波峰和波谷的动态起伏。因此，城市的分区只是其街道密度变化速率的一种折射现象。不同的功能分区或社会聚集本质上对应于不同尺度上空间彼此连接的紧密程度的变化，通过这种变化使得某些功能混合聚集在一起，同时使得某些功能主导性地占据城市某些位置，甚至排斥其他功能的侵入。在很大程度上，街道密度本身只是局部的结果表现，而街道密度的变化率则体现街道之间的彼此连接程度，后者才是城市富有多元活力的几何形体的支撑。因此，从实践的角度，我们不仅要关注小街区和密路网，而且更要关注街区大小或路网密度变化的方式及其所对应的功能混合、整合或甚至排斥。从而，我们可获得更为多样而有机的城市复杂整体，其中有小街区、中街坊、大院以及商业步行街、高速公路等城市多元要素。正如最近的空间句法研究表明：街道本身就是社群交流的场所，不同的连接方式推动了不同程度的社会融合和交流。当我们从不同的尺度以及不同的空间连接方式去看待城市的时候，也许我们看到的是不同维度的城市空间及其功能活动。空间的构成关系也许促进了社会经济活动的分类或融合，然而社会经济活动的分类本身同样也使得空间的连接紧密程度得以分化。于是，在物质空间建设与社会经济活动之间，空间连接程度成为一种互动的界面，而这种界面的密度变化成为一种分类的工具。