轨道检测系统钢轨图像标定误差试验研究

2019-08-08王琰

铁道建筑 2019年7期

关键词：靶标钢轨标定

王琰

(1.中国铁路总公司铁路基础设施检测中心，北京 100081；2.中国铁道科学研究院集团有限公司基础设施检测研究所，北京 100081)

图1 钢轨图像线结构光视觉测量示意

1 评判方法和模型

1.1 标定数学模型

钢轨图像线结构光视觉测量组件的标定[11-17]是建立物空间平面坐标和像空间平面坐标之间的数学映射关系。标定后可由相机采集钢轨图像并反算出图像任意点的真实物理坐标，进而计算出钢轨的几何参数。当前钢轨图像线结构光视觉测量组件采用针板靶标标定方法。该方法基于小孔成像原理，即物空间平面中任意一点都会唯一映射到像空间平面中的一个像素点，并通过数学模型构造出物空间平面物理坐标与像空间平面图像坐标之间的数学映射关系。物空间中一个由若干已知空间距离的特征点构成的特征平面BDEF，被相机成像映射在像空间特征平面bdef上，如图2所示。

图2 物空间平面与像空间平面数学映射关系

假设物空间特征平面BDEF由m个特征点组成，第k个特征点的物理坐标为(Xk,Yk)，映射到像空间特征平面bdef对应点的图像坐标为(uk,vk)。物空间特征点和像空间特征点坐标信息已知，则物空间特征平面BDEF和像空间特征平面bdef的数学映射关系为

(1)

(2)

式中：n为阶数；aij和bij为标定系数。

X(u,v)与Y(u,v)的误差函数分别为EX与EY，即

(3)

(4)

式中：m为物空间平面特征点总数。

钢轨图像标定采用最小二乘法计算标定系数aij和bij，即

(5)

(6)

由此可建立钢轨图像标定数学模型，像空间任意一点的坐标(u,v)均可映射到物空间对应点的坐标(X,Y)。

1.2 一维相机投影模型

为了简化相机投影模型，直观分析钢轨图像标定误差，本文从几何光学角度建立一维模型，在靶标深度方向进行误差分析。模型如图3所示，其中z轴为靶标深度方向。当激光器投射出的线激光垂直切割针板靶标钢针时，线激光面与靶面共面，即靶面倾斜角δ为0°。相机采集靶标图像，靶标靶面z轴方向不同位置的特征点在相机成像面上对应不同投影位置的像素点。靶标z轴方向特征点位移变化ΔH，则对应相机成像平面上光点位移变化Δh，根据几何关系建立2个变量的数学模型，即

(7)

式中：l为靶标靶面z轴与物镜光轴的交点到物镜的距离；θ为靶标靶面z轴与物镜光轴的夹角；d为物镜焦距。

支气管堵塞主要发生在管理条件差的鸡场，该病一年四季均有发生，但以春秋冬季节高发，近年来季节性趋于不明显，呈增长性发病趋势。

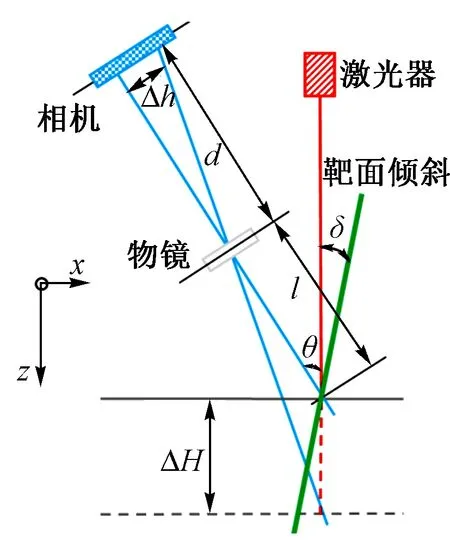
图3 靶标深度方向一维相机投影模型

在相机成像平面上像的大小表示为像素个数，h0为单个像素大小，t为像素个数，则成像平面上光点位移变化为

Δh=h0t

(8)

2 试验设计及分析

对钢轨图像针板靶标标定方法建立数学映射模型的关键是物空间坐标和像空间坐标必须已知且准确。GJ-6型轨道检测系统钢轨图像标定方案如图4所示。当钢轨图像线结构光视觉测量组件的激光器投射出的线激光垂直切割针板靶标阵列钢针时，形成结构光光点阵列，光点阵列面与线激光投射面共面且平行于针板靶标靶面，则光点阵列间距即为已知的针板靶标钢针阵列间距，由此获得已知的物空间坐标。钢轨图像线结构光视觉测量组件的相机采集针板靶标线结构光光点阵列图像，采用重心法提取像空间图像点阵列各点的像素重心坐标，由此获得已知的像空间坐标。

图4 钢轨图像标定方案

但是从获取物空间坐标和像空间坐标2方面设计试验有可能导致误差：一是针板靶标靶面倾斜导致物空间坐标获取不准确；二是针板靶标成像像素点偏移导致像空间坐标获取不准确。下文研究针板靶标靶面倾斜及成像像素点偏移对钢轨图像标定误差的影响。

以GJ-6型轨道检测系统钢轨图像线结构光视觉测量组件结构参数为基础，建立靶标深度方向一维相机投影模型(参见图3)。钢轨图像线结构光视觉测量组件结构参数见表1。定义靶面z轴方向上一维坐标为0的点为起始点，起始点两侧分别以1 mm物理空间间距等距离取30个点，靶面z轴方向特征点集的一维坐标Zk∈[-30,30]，k=1,2,3,…,60。理想情况下标定时δ=0°，根据式(7)、式(8)可得到靶面z轴方向特征点集的一维坐标在像平面上对应的像素位移分布Uk，k=1,2,3,…,60。基于钢轨图像针板靶标标定数学模型，根据式(1)、式(3)、式(5)计算得到标定系数，即确定靶标像平面与物平面的数学映射关系，从而实现钢轨图像一维标定。

表1 钢轨图像线结构光视觉测量组件结构参数

2.1 针板靶标靶面倾斜标定误差

设定针板靶标靶面倾斜2°，即δ=2°，根据式(1)、式(3)、式(5)可以获得针板靶标靶面倾斜2°时的标定系数，进而可计算出针板靶标靶面倾斜2°时的物空间特征点位置Zk2。与理想情况下物空间特征点位置Zk比较，即可获得针板靶标靶面倾斜2°时的物空间特征点位置偏差分布，见图5。可知，针板靶标靶面倾斜2°时，在靶标深度方向上靶标中间误差最小，两端误差较大，最大值为1.9 mm。

图5 针板靶标靶面倾斜2°时物空间特征点位置偏差分布

采用以上方法计算得到靶标靶面倾斜角δ为1.5°，1°，0.5°时标定误差的最大值分别为1.5，0.9，0.3 mm，且在靶标深度方向上靶标中间误差最小，靶标两端误差较大。

2.2 成像像素点偏移标定误差

在理想情况下标定时δ=0°，靶面z轴方向特征点集的一维坐标在像平面上对应的像素位移分布为Uk，k=1,2,3,…,60。在像平面每个理想投影点位置加一个随机偏差变量ε∈[-1,1]像素，得到带像素偏差的投影点，根据式(1)、式(3)、式(5)计算得到带像素偏差的标定系数，根据式(7)反算出带像素偏差的物空间坐标点Zε2。与理想情况下物空间特征点位置Zk比较，即可获得像素偏差ε∈[-1,1]像素时物空间特征点位置偏差分布，见图6，标定误差以mm计在[-0.09,0.07]。像素偏差随机变量变化时，选取3组试验分别计算物空间特征点位置偏差分布，结果见表2，可知成像像素偏差越大，反算出物空间特征点位置偏差也越大。