“比”出精彩 “较”出真知
2019-08-07魏世远
魏世远
[摘 要]在“以学生的发展为本”这一理念的指导下,研究学生的“学困点”,以学定教,有效化解疑难,成为提高课堂教学效率的关键。比较法在帮助学生建立知识的联系与区别、整合知识点等方面有着明显的优势,可以有效地帮助学生突破“学困点”,提高学生的学习效率。
[关键词]学困点;比较法;小学数学
“学困点”是指学生在数学学习过程中因相似内容互相混淆、学习内容负向迁移、知识点螺旋递进等原因所产生的困惑点,也可将其理解为教学中的疑难问题。
为了突破“学困点”,教师往往在课前精心选择习题,在课堂上将大量的习题呈现给学生,期待在大量的练习中达到复习巩固以及攻坚克难的目的。但课堂实践表明:课堂上大量的练习未必能达到教师预期的效果,严重的甚至会使学生产生“逆反”的心理。
那么,用怎样的方式可以有效帮助学生突破“學困点”,提高学习效率呢?根据笔者多年的教学经验和学生的学习反馈情况,比较法在帮助学生建立知识的联系与区别、整合知识点等方面有着明显的优势,可以有效解决上述问题,提高学生的学习效率。
一、相似内容比较迁移
错误原因分析:这题是常见的复名数与单名数之间的转化题型。有部分学生审题不清,只是简单地对原数据进行了单位换算,也有部分学生对于单名数与单名数、单名数与复名数、复名数与复名数之间的转化方法混淆不清,没有掌握正确的方法。

化解策略:
师:同学们发现了什么?
生1:下面一题比上面一题多了一个“=”。
生3:两题相差一个“=”,意义就完全不一样了。
师:同学们听明白了吗?谁再来清楚地说一说?(指一个学生说,然后同桌之间相互说一说)
师:虽然两题只相差一个“=”,但区别是相当大的。因此,我们在转化的时候不能只是简单地拆分数据,一定要仔细地看清题目。
相似内容联想比较迁移举例:

1.学生在学习了六年级下册第一单元负数,知道了0既不是正数,也不是负数,在课接近结束时,可要求学生用“……既不是……也不是……”对学过的数学知识进行造句。有的学生会联想到五年级下册学过的“1既不是质数,也不是合数”;比较正(负)数与质(合)数各自是按照什么标准来划分的,再次明确正(负)数是表示相反意义的量,按大小区分,质(合)数是按因数个数的多少区分。
2.教学六年级上册倒数的意义时,与四年级学过的垂直、平行的定义相联系,突出两个数之间相互依存的关系,强调倒数不能单独存在。
3.学习了六年级上册比的基本性质后,联想之前学过的商不变性质、分数的基本性质,它们与比的基本性质在实质上是一致的。通过下表,可以清晰地看出除法、分数、比之间的相通点:
对相近的内容进行比较,可以更好地把零散的知识点串联起来,形成知识链,让学生主动地迁移知识、整合知识,有利于学生深化对所学知识意义的有效理解。
二、易混淆内容比较区分
题目:小军的飞机模型在空中飞行6分钟,小峰的飞机模型飞行时间比小军短[13]分钟。小峰的飞机模型飞行了( )分钟。
错解:小峰的飞机模型飞行了( 4 )分钟。
错误原因分析:学生受到解决分数(百分数)问题思维定式的影响,审题不仔细,
化解策略:
师(出示错例):同学们,发现问题出在哪了吗?

生:后面有单位名称,是数量,
师:审题不仔细,结果做错了。那你们以后读题时该怎么做呢?
出示对应练习题:
1.苹果比香蕉多5个,香蕉比苹果少( )个。
2.苹果比香蕉多[15],香蕉比苹果少( )。
学生有如此的发现能力,对单位“1”理解得如此透彻,且用字母表示数如此到位,令我感到意外和惊喜。
类似会引起负迁移的内容比较举例:
1.在第一次解方程时,全班有32.8%的学生是“左边乘5,右边也乘5”,经过多次讲解订正,虽然错误率有所降低,但部分学生几天后还是“老调重弹”。分析原因,学生是受到了六年级上册分数除法负迁移的影响,这时,可以出示让学生比较两个方程在解法上的相同点与不同点,最后概括出结论:解此类方程时,左右两边同乘除数,而非其倒数,这跟分数除法是有本质区别的。
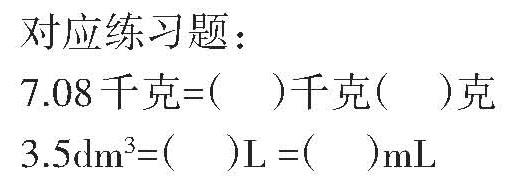
2.一个圆锥体金属铸件的底面半径是4cm,把它浸没在底面半径是6cm的圆柱体玻璃水槽内,水面升高了2cm(水未溢出),求这个圆锥体金属铸件的体积。较多学生看到求圆锥体体积,马上想到圆锥体的体积公式。这时,把圆锥体改为一块不规则的光滑的石头(不吸水),能否求出石头的体积?结论是可以求出石头的体积。再把圆柱体容器改为长方体(或正方体)容器,还能求出水中物体的体积吗?最后通过多次比较得出:求浸没在水中的物体的体积,就是求容器中水上升部分空间的体积,跟容器的形状有关,跟放在水中物体的形状无关。如此,把圆柱体与长方体、正方体紧紧联系起来,便可形成知识链。
三、知识深化比较提升
此题学生错误率较高,究其原因,主要是分数的数量关系没搞清楚。
化解策略:
出示就是求什么?(速度)要求每小时走多少千米,就是把10千米平均分成2份,求每份是多少?(速度=路程÷时间)。再同原来的题目进行比较,找出异同点,发现原题只是把整数变为分数,其他意義完全相同。

知识间比较提升举例:
1.推导圆柱体体积计算公式时,让学生观察圆柱体转化成近似长方体的模型,问:什么没变?什么发生了变化?(体积相等,表面积发生了变化,增加了2个“半径×高”的长方形)引导学生回想上学期把圆转化为近似长方形后,面积不变,周长增加了两条半径。比较得出:平面图形(圆)转化时增加周长,立体图形(圆柱体)转化时增加表面积。

2. 学习了“圆柱体体积=底面积×高”,长方体、正方体、圆柱体都是柱体,求体积都能用“底面积×高”后,问:圆柱体的侧面沿高剪,展开后是长方形,侧面积=底面周长×高,长(正)方体有这个特点吗?

通过剪一剪,可以发现,长(正)方体的侧面积=底面周长×高。
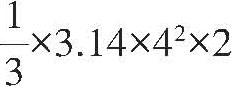
学生“学困点”的产生原因是多方面的,可能来自于教材,也可能来自于教师或学生本身。同时,不同的教学背景使得不同班级学生的“学困点”也不尽相同,而“比较法”可以较好地帮助学生突破“学困点”。当然,这需要教师透彻地理解教材,摸透学生错误的源头所在,有的放矢,对症下药,只有这样才能让数学核心素养的培养落地生根。
(责编 罗 艳)
