基于熵视角的金融风险度量

张金波,赵 攀

1 引言

金融市场是一个异常复杂的系统，主体包括生产者、投资者、消费者、金融中介机构和为数不少的投机者等。诸多类型的参与者以及他们不同的投资心理注定了金融市场的复杂性。然而，迄今为止，多数学者对金融市场的研究都是在资本市场理论的线性分析范式下进行的。 研究人员往往把复杂系统过于简单化，假定市场是有效的，投资者是理性的，信息是透明的，价格的变化是随机游走的等。这些不是很贴切的条件限制导致了经典的线性化分析方法的缺陷逐渐被暴露出来。例如，它无法解释资产收益的“厚尾”[1]、“波动聚集”[2]、“蝴蝶效应”[3]、“黑色星期一”[4]等现象。事实上，系统内、外部各种因素是通过复杂的非线性相互作用进行影响的。

1865年，德国物理学家克劳修斯提出了熵的概念，用来解决物理学中的热力学问题，得到了著名的热力学第二定律：孤立系统的运动是一不可逆过程，且总是朝着系统熵增加的方向进行演变，故热力学第二定律又被称为熵增原理。熵定律很快被人们发现它具有普适性，不仅可以描述热力学系统还可以运用在管理学、决策学、安全学等[5-7]，只要系统中存在大量的微观状态都是可以适用的。金融市场中存在着大量的投资主体，无时无刻不在物质、能量和信息交换，因此，熵定律在金融市场这个庞大而复杂的系统同样也是适用的[8]。文献[9]阐述了熵可以更好地揭示股票交易的紊乱性和不确定性；文献[10]将信息熵与方差对不确定性的度量进行了比较，表明信息熵和方差在度量样本集中性时是不同的，方差是围绕着均值波动的，而信息熵是没有固定的参照点。文献[11]认为我们无法确定金融市场各因素的真实分布，用信息熵来度量不确定性会比方差更加合适。文献[12]给出了股票熵的计算方法。文献[13]给出了实物期权定价的熵理论模型，避免了传统期权定价模型过多依赖参数和假设的不足，并合理地解释了企业决策信息的重要性。

文章的主要工作是探讨熵理论在股票市场中的适用性，建立基于熵理论的股票系统风险度量方法，选取国际上具有代表性的美国标普500、英国富时100和中国上证三大指数进行了实例分析，结果表明熵可以较好地度量股票系统的风险。熵作为研究复杂系统的有力工具，在金融市场中应有很好的用武之地，本文只是尝试，希望能起到抛砖引玉的作用。

2 模型的建立

我们把股票金融市场看作一个复杂的系统，系统状态的不确定导致了投资者的实际收益往往与期望收益不一致，这种收益的不可预期便是投资者的风险，同时，它也代表着金融市场的风险。投资风险可以描述为收益率的不确定状态和该状态发生的概率。物理学中熵就是通过构造状态发生概率的函数来度量系统的不确定性，我们把熵运用在金融系统中便可以度量金融系统的不确定程度，即金融系统的风险。

假设投资者投资方案的状态空间为Ω:={ω1,ω2,…ωn}，状态ωi,i=1,…,n的概率为pi，则金融熵为

(1)

它的大小表示了投资者投资收益的不确定程度，从而代表了金融系统的风险大小。物理中熵理论告诉我们，一个孤立的系统它的熵值会逐渐变大，直到该系统最终消亡殆尽。根据上述熵增理论，我们可以认为熵值函数的最大值便是系统崩溃时的熵值。由数学知识可知熵值函数(1)式存在唯一最大值，而且，当各状态的概率相同时熵函数值最大为ln(n)。那么，系统熵值除以系统崩溃熵值便代表了系统距离崩溃状态的大小，定义为系统崩溃系数ρ，易知0≤ρ≤1，ρ越趋向于0说明系统越稳定，ρ越趋向于1说明系统的不确定性越大，越不稳定。

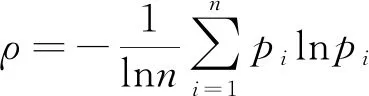
(2)

3 模型的应用

表1 上证指数系统的熵值和崩溃系数

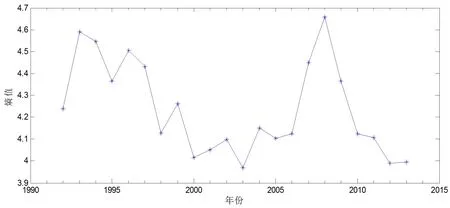
图1 上证指数系统的熵值变化

图2 上证指数系统的崩溃系数的变化

从表1我们可以看出，上证指数在经历过的22年间中，其熵值有19年在4以上，只有2003,2012,2013三年在4以下，即使这三年的熵值小于4，但2003年最小的熵值也达到了3.9675，系统崩溃系数大都在0.7之上，小于0.7的只有4年。从图1和图2可以发现，熵值及崩溃系数在1992年到1993年增加较大，然后，从1993年到2003年基本是逐渐减小的过程，至2003年达到最低，此后，从2003年到2006年是逐渐增加的过程，2006年到2008年又是迅速增加，到2008年达到顶峰，随后，从2008年到2010年迅速下降，2010年到2013年又逐渐减小。

上述变化切实地反映了中国股票市场的发展历程，在1992年至1997年之间，中国股票市场实际上是没有涨跌停板限制，加上股票市场刚刚诞生，几乎没有基金等投资机构，绝大多数是个人投资者或投机者，市场监管制度还没建立和完善，股指的波动十分剧烈，如，在1992年11月到1993年2月短短3月时间，股指从386点一路猛涨到1558点，涨幅超过了300%。与此对应的这个期间的股指系统崩溃系数都比较大基本上都在0.75以上，1993年更是达到了0.7959。1998年至2006年间，市场发展逐步成熟，整体比较平稳，股指没有出现急剧的涨跌现象，股指系统风险较小，这个时期的股指系统崩溃系数基本在0.71附近。2007、2008和2009年股指从998点上涨到6124点，随后又跌至1664点，短短的三年时间股指完成了一个巨大的过山车运动，上涨期间的平均月涨幅超过25%，下跌期间的平均月跌幅也超出了20%，可见股指的波动之大，这三年的系统崩溃系数都在0.76以上，而且2008年的系统崩溃系数达到了22年中的最高值0.8074。2010年至2013年，经过前期的大跌，市场活跃度明显降低，股指运行整体平稳，系统崩溃系数都在0.72以下。

总的来讲，上证股指系统崩溃系数较好地刻画了股票市场的系统风险，从这22年的股指系统崩溃系数，我们可以得出在崩溃系数小于0.7时，股票市场比较低迷，系统风险较低，基本是处于“熊市”的底部，投资者这时进入市场风险较低；在崩溃系数处于0.7—0.73时，股票市场相对比较活跃，但风险不大，基本上属于正常波动；当系统崩溃系数超过0.73时，股票市场波动十分剧烈，风险较大。在22年里，上证股指系统崩溃系数只有2008年超过了0.8为0.8074。

为了进一步研究该模型在股票市场的适用性，下面选取国际上有代表性的美国标普500和英国富时100两大著名股票指数进行实例分析(时间为1993年—2013年，数据来源RESSET金融研究数据库)，虽然这两大股指没有实行涨跌停板制度，但通过计算发现日收益率超出[-10%,10%]情况并没有发生，故我们可按照计算上证股指熵值和崩溃系数的步骤来计算这两大股指的熵值和崩溃系数。

表2 标普500指数系统的熵值和崩溃系数

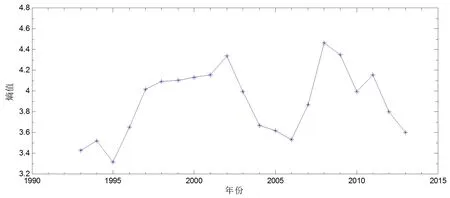
图3 标普500指数系统的熵值变化

图4 标普500指数的系统崩溃系数的变化

表3 英国富时100指数系统的熵值和崩溃系数

图5 英国富时100指数系统的熵值变化

图6 英国富时100指数的系统崩溃系数的变化

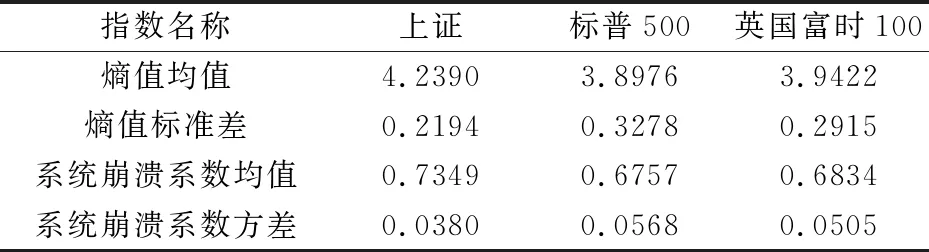
表4 上证、标普、富时三大股指的熵值和崩溃系数的统计特征

指数名称上证标普500英国富时100熵值均值4.23903.89763.9422熵值标准差0.21940.32780.2915系统崩溃系数均值0.73490.67570.6834系统崩溃系数方差0.03800.05680.0505

图7 上证、标普、富时三大股指的熵值比较

图8 上证、标普、富时三大股指的系统崩溃系数比较

从表4可以看出，在1993—2013这21年中，上证指数的熵值平均值为4.239，标普和英国富时指数的熵值平均值为3.8976和3.9422，上证指数的系统崩溃系数平均值为0.7349，标普和英国富时指数的分别为0.6757和0.6834。说明了整体上来讲，中国上证股指与标普和英国富时股指相比系统的不稳定性较大。从图8我们也可以看出：1)上证的系统崩溃系数与标普和英国富时的崩溃系数存在着较大差异，显著运行在标普和英国富时之上，说明上证股指与标普和富时相比较不稳定；2)标普和英国富时的系统崩溃系数的变化趋势极为相似，说明了标普和富时两个股指系统有着相似的运行规律；3)三大股指的系统崩溃系数均在2008年金融危机时达到了最大值，但只有中国上证股指的系统崩溃系数超过了0.8。

4 结束语

金融市场通常受到市场内、外诸多因素影响，它是一个异常复杂的巨大系统。文中借助物理学中的熵理论，从复杂系统的角度对其运行规律进行了研究，得出了中国股市的系统稳定性要比西方成熟市场的差，西方著名的美国标普500和英国富时100两大股指的系统稳定性及其变化规律极为相似，提出了度量股指系统风险的系统崩溃系数定量度量方法。该方法也可用于度量和预测单支股票或其他系统的不确定性。熵理论在金融市场中的应用还需更深入地研究，希望本文能起到抛砖引玉的作用。