桥梁时变可靠度指标的改进粒子滤波预测算法
2019-08-07樊学平刘月飞
樊学平, 屈 广, 刘月飞
(1.兰州大学 土木工程与力学学院, 甘肃 兰州 7300001; 2.兰州大学西部灾害与环境力学教育部重点实验室, 甘肃 兰州 730000)
目前,结构健康监测(structural health monitoring, SHM)领域的研究主要集中在利用传感器采集数据和监测数据的应用两个方面.前者主要集中在数据压缩、数据恢复、数据获得技术和系统组装技术等方面[1-5],目前在硬件和技术上已经趋于成熟,对于后者而言,国内外学者的研究主要集中在结构损伤识别、结构模态参数识别以及结构模型修正等方面[6-8].基于SHM数据的桥梁可靠性预测及评定,国内外学者多是基于离线监测信息展开研究[9-13],而基于实时监测信息的结构性能动态预估相对较少,且离线的结构性能预测及评定模型在实际工程应用中存在一定局限性,如:基于一次回归函数与常值函数的桥梁可靠性预测分析[9-10],均未考虑监测变量的随机性和非平稳性;基于ARMA(autoregressive moving average model)模型的桥梁构件荷载效应预测[11],以及基于单一或组合贝叶斯动态模型的桥梁可靠性动态预测[12-13],多是基于平稳监测信息进行可靠性分析,而考虑到桥梁动力响应的复杂性,基于非线性及非平稳监测信息的结构性能预测方法还需进一步研究.近年来,粒子滤波器因在非线性问题中出众的性能而倍受关注[14].在SHM领域中,粒子滤波器在结构应力预测、结构可靠性动态预测、结构系统识别以及结构损伤识别等方面已取得一些研究成果,如:基于高斯混合粒子滤波器、改进高斯混合粒子滤波器以及折扣高斯粒子滤波器的桥梁可靠性预测[12,15-17].但粒子滤波器假定重要性采样是指能够从一个合理的后验建议密度函数中得到一组覆盖真实状态的样本集合.因此,找到一个最优建议密度函数来指导采样过程,就能大大提高粒子的利用率,进而可以有效降低粒子退化的影响,提高系统的识别精度.桥梁长期运营中,由于其构件受到多种荷载耦合作用,SHM系统所获取的结构动力响应数据十分复杂,并且受诸如气候条件、桥下水位等外在环境因素影响较大,因此桥梁应力(或挠度)状况时常会出现变化,这就要求所选取的粒子滤波建议分布具有长期稳定性、受外界干扰小、精度高等特点,并且具有能随桥梁状况变化而不断更新的良好自适应性.因而,如何选取具有以上特性的建议分布就成为利用粒子滤波方法预测桥梁时变可靠性的难点所在.
为合理应用监测信息对桥梁动态可靠度指标进行实时在线预测分析,基于桥梁监测极值应力(或挠度)信息,利用贝叶斯动态线性模型和粒子滤波器相融合的改进粒子滤波预测算法,结合FOSM(first order second moment)方法对桥梁可靠度指标进行了动态预测,并进行了实例和设计试验验证分析.改进粒子滤波方法利用贝叶斯动态线性预测模型为动态粒子提供建议分布,并充分利用动态健康监测数据对建议分布进行递推更新,有效提高了粒子的利用率,并且引入贝叶斯动态模型折扣因子[12],使得粒子滤波在递推过程中具有较好的自适应性.
1 监测数据的动态模型
SHM系统在长期运营过程中积累了大量监测应力(或挠度)信息,定义每小时(或每天)监测应力(或挠度)的极大值为监测极值应力(或挠度)信息.定义{Xt,t=1,2,…}为极值应力(或挠度)状态时间序列,Xt表示t时刻的极值应力(或挠度)状态.所建动态方程基于以下两点假设:
(1) {Xt,t=1,2,…}具有马尔科夫性.
(2) 监测信息{Zt,t=1,2,…}之间相互独立,且Zt仅和状态变量Xt相关,Zt与Xt呈线性关系.
桥梁极值应力(或挠度)的动态模型如下:
状态方程为
Xt=f(Xt-1)+wt,wt~N(0,Wt)
(1)
监测方程为
Zt=Xt+vt,vt~N(0,Vt)
(2)
初始状态信息为
p(Xt-1|Dt-1)=N(mt-1,Ct-1)
(3)
式(1)~(3)中:Xt为状态变量;f(·)为状态转移函数,可以通过极值应力(或挠度)监测数据利用五点三次平滑处理之后的时间序列近似回归拟合得到[12];wt为状态白噪声;Wt为状态误差的方差;Zt为t时刻的极值应力(挠度)监测值;vt为监测白噪声;Vt为监测误差的方差;初始状态变量的概率密度函数(probability density function, PDF)p(Xt-1|Dt-1)可根据既有极值应力(或挠度)信息平滑得到的时间序列样本统计得到;N(·)为正态PDF.
基于先验信息集Dt和当前监测数据Zt+1估计状态Xt+1的后验PDF,即p(Xt+1|Dt+1),求解过程包含以下两个阶段:
(1) 预测.已知t时刻状态的后验PDFp(Xt|Dt),利用式(1)可得t+1时刻状态Xt+1的先验PDF为
(4)
(2) 测量更新.在t+1时刻,利用当前监测极值Zt+1,由Bayes公式更新式(4),可得后验PDF为
(5)
其中
p(Ztt+1|Xt+1)dXt+1
(6)
为极值的一步预测PDF.
2 改进的粒子滤波算法
结合重要性采样与重采样方法,改进的粒子滤波器(IPF)通过蒙特卡罗方法以参数化的分布逼近式(4)和式(5)中的预测PDF与后验状态PDF,是式(4)和(5)近似求解的一种策略.
2.1 基于BDLM(Bayesian dynamic linear model)的近似重要性采样分布
粒子滤波的有效性依赖于重要性采样分布的合理性.较为合理的重要性采样分布能够有效减少具有偏差的样本,提升粒子滤波性能.因此,引入BDLM[12]在重要性采样阶段近似产生重要性采样PDF.假设采样过程中抽取了n个粒子,则更新粒子集合的步骤如下:
(1)t时刻每个粒子的状态后验PDF为
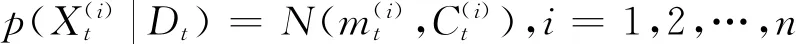
(7)
(2)t+1时刻的状态先验PDF为

(8)
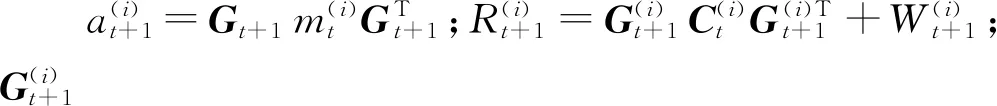
(3)t+1时刻的一步预测PDF为

(9)
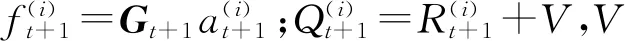
(4)t+1时刻的状态后验PDF为

(10)
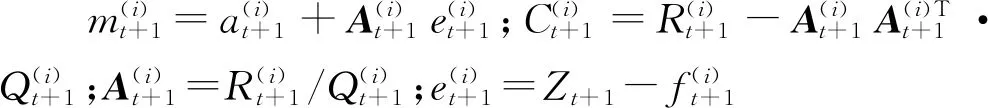
式(10) 用来近似模拟重要性采样分布.
2.2 改进的粒子滤波算法
粒子滤波器能够为监测值与状态值的后验概率分布进行高精度表达[18],在非线性系统中具有出色的表现.然而,传统粒子滤波器以给定的高斯分布作为建议分布,并没有充分利用最新监测信息对建议分布进行动态更新[19],因此通常需要大量粒子样本来近似接近系统的后验PDF,并且在状态更新时计算量较大,具有一定盲目性.特别是当桥梁的应力(或挠度)环境发生变化时,由粒子滤波产生的样本就会出现较大偏差.因而有效减少样本数量的自适应采样策略是该算法的重点所在.因此,将自适应性及鲁棒性良好的BDLM应用到粒子滤波中,为其提供重要性采样,不仅可以获取更为准确的建议分布,而且能够提升粒子滤波算法的鲁棒性与自适应性,同时大大减少了粒子滤波算法的样本需求量,降低了算法复杂度.
改进后的算法步骤如下:
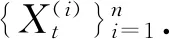
(2) 由式(7)~(10)递推得到每个粒子的建议分布,亦即在t时刻用BDLM以及最新监测信息Zt+1更新粒子,则第i个粒子更新为

(11)
利用式(2)、(8)和(11)可得粒子权重为

(12)

将权重进行归一化,可得

(13)
(3) 利用重采样算法[20],根据归一化权值的大小对粒子集合进行复制和淘汰.
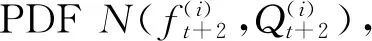

(14)
(6) 重复(2)~(5)步,可实现监测变量的动态预测.
一步预测精度可由均方误差(EMSE)来衡量,即

(15)
显然,均方误差越小,预测精度越高.
改进算法流程如图1所示.
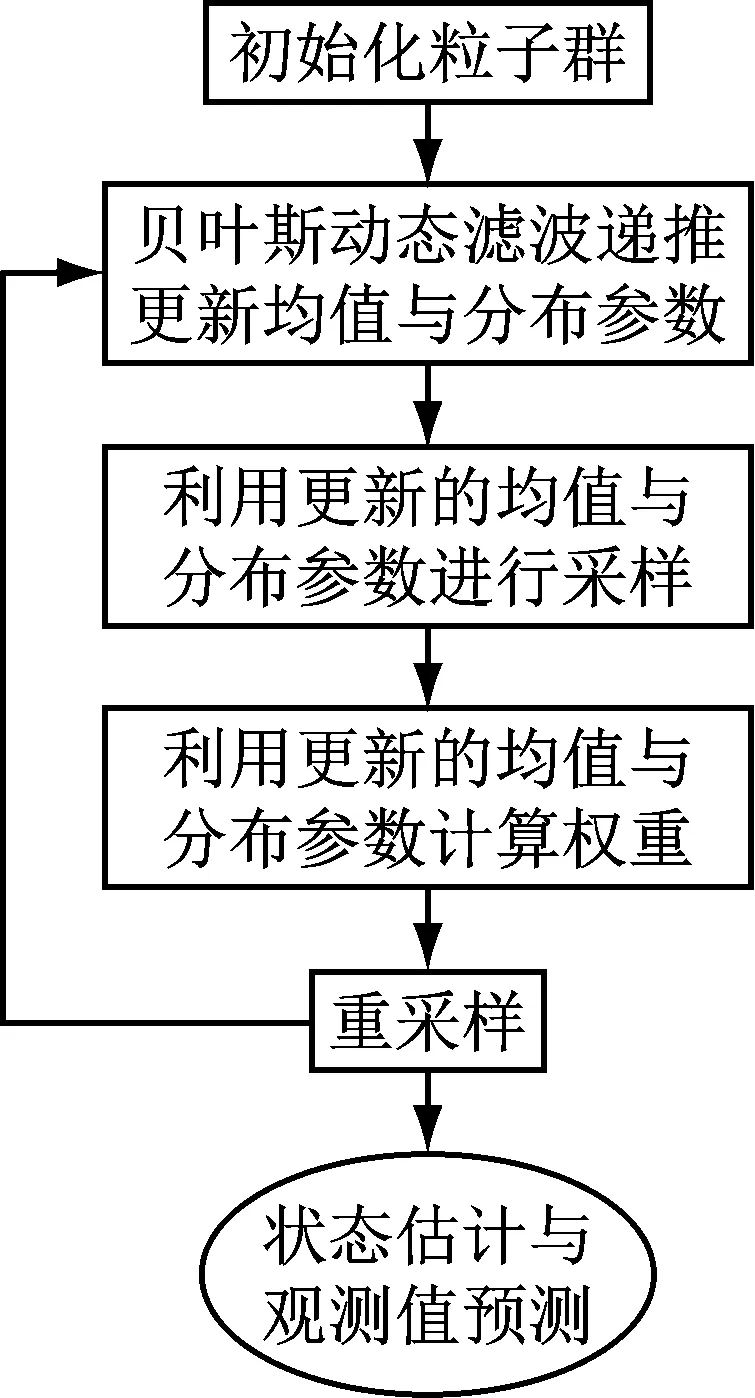
图1 改进的粒子算法流程
3 可靠度指标预测计算
3.1 工程实例1预测公式
基于天津富民桥主缆的应力监测数据,结合FOSM方法对主缆可靠性进行动态预测.主缆钢丝的抗拉强度按照[σ]=1 670 MPa进行计算,主缆截面失效模式对应的功能函数为
g(σp,t)=[σ]-σp,t
(16)
式中:σp,t为t时刻预测的极值应力,且随机变量之间相互独立.
主缆钢丝抗拉强度的平均值为μσ=1 670 MPa,变异系数δσ=0.15,则利用FOSM方法可得主缆的动态监测可靠度指标βt为

(17)

考虑到预测过程的不确定性与随机性,则动态可靠度指标预测公式为

(18)
式中:μσp,t和Vσp,t分别为t时刻主缆极值应力基于改进粒子滤波器的一步预测均值和方差.
本算例中的极值应力为每小时监测应力的极大值.
3.2 工程实例2预测公式
参考已有文献[12],可得美国I-39北桥第二跨横梁可靠度指标预测公式为

(19)
式中:μM和σM分别为基于改进粒子滤波器预测得到的极值应力平均值和标准差;μR和σR分别为按照规范计算的抗力的平均值和标准差;μS和σS分别为由钢板恒载所引起的应力的平均值和标准差;μC和σC分别为由混凝土恒载所引起的应力的平均值和标准差;γM=1.15是传感器的修正系数.
由文献[12]可知:μR=380 MPa,σR=26.6 MPa,结合由结构自重产生的应力分布参数,μS=116.3 MPa,σS=116.3 MPa×0.04=4.65 MPa,μC=108.8 MPa以及σC=108.8 MPa×0.04=4.35 MPa,可得第二跨横梁的可靠度指标预测公式为

(20)
参考式(17),可得第二跨横梁的可靠度指标监测值βt为

(21)
式中:Mt为t时刻的极值应力监测值.
本算例中的极值应力为每天监测应力的极大值.
3.3 工程实例3预测公式
参考已有文献[12],可得伊通河桥上游主梁动态可靠度指标预测公式为
(22)

参考式(17)和(21),可得主梁动态可靠度指标监测值βt为

(23)
式中:f(t)为t时刻的极值挠度监测值.
本算例中的极值挠度为每小时监测挠度的极大值.
4 算例分析
4.1 工程实例1计算分析
天津富民桥的结构及其示意图分别如图2和图3所示.富民桥总长340.3 m,桥宽40 m.桥梁动力响应复杂,结构受温度荷载影响较大.基于此悬索桥主缆的监测信息,对主缆可靠性进行动态预测.

图2 天津富民桥

图3 富民桥结构示意图
此主缆共安装了2个传感器,取其中历史监测极值应力绝对值较大的FBG01192传感器作为实时监控对象.定义每小时监测应力的最大值为监测极值应力.从2009年8月1日到2009年9月3日,对此桥进行了810 h的健康监测.其中前300 h的监测极值应力如图4所示.对其采用五点三次平滑方法[9]处理后的数据如图5所示,处理后的数据近似作为初始状态信息,此初始状态信息用正态PDF模拟.

图4 极值应力监测值(工程实例1)

图5 极值应力初始值与监测值(工程实例1)
采用前300 h的极值应力信息,并结合式(1)~(3),建立的动态模型如下:
状态方程为
Xt=Xt-1-0.006 6+wt,wt~N(0,Wt)
(24)
监测方程为
Zt=Xt+vt,vt~N(0,0.103 2)
(25)
初始状态信息为
Xt-1|Dt-1~N(147.634 1,6.261 7)
(26)
利用改进的粒子滤波算法,结合式(7)~(15)与式(24)~(26),基于第300小时到第809小时的监测极值应力数据,对第301小时到第810小时的极值应力进行实时动态一步预测,结果如图6所示.一步预测均方误差可由式(15)计算,连续50次滤波结果的EMSE见图7.可以看出,一步预测值与实测值几乎重合,并且均方误差较小(0.068左右波动)且平稳可观,验证了模型对于监测应力预测的有效性.将预测结果与基本粒子滤波(PF)[21]及差分自回归移动平均模型(ARIMA)[22]进行比较,预测结果对比如图8所示.经计算得到粒子滤波的均方误差为0.146 8(平均50次滤波EMSE的均值),ARIMA模型的均方误差为0.475 8.由此可见改进粒子滤波器的预测精度十分可观,进一步验证了所提模型的准确性.

图6 基于改进粒子滤波器的极值应力预测值与实测值(工程实例1)
Fig.6Monitoring and predicted extreme stresses based on IPF

图7 连续50次滤波的预测均方误差(工程实例1)

图8 3种算法极值应力预测结果比较(工程实例1)
结合式(17)和式(18)对主缆可靠性进行实时预测分析,得到结果如图9所示,可以看出可靠度指标预测值与实测值几乎重合,很好地预测了可靠度指标的变化趋势,而考虑了不确定性与随机性的可靠度指标预测值略低于实测值,但由于考虑了不确定性,预测结果更符合工程实际.

图9 可靠度指标的实测值与一步预测值(工程实例1)
4.2 工程实例2计算分析
采用美国I-39北桥第二跨横梁83 d的极值应力监测数据对所提算法进行验证.极值应力数据如图10所示.

图10 极值应力监测值(工程实例2)
首先基于前50 d的监测极值应力数据,结合式(1)~(3)建立动态模型如下:
状态方程为
Xt=Xt-1-0.056 3+wt,wt~N(0,Wt)
(27)
监测方程为
Zt=Xt+vt,vt~N(0,8.814)
(28)
初始状态信息为
Xt-1|Dt-1~N(24.335 1,7.138 7)
(29)
然后采用所提IPF预测算法,结合式(7)~(15)与式(27)~(29),基于第50天到第82天的监测极值应力信息,对第51天到第83天的极值应力进行动态预测,预测结果如图11所示.并与PF[21]及 ARIMA[22]进行比较,预测结果如图12所示.利用式(15)得到IPF、PF以及ARIMA(0,0,0)的EMSE分别为18.897 7、37.612 7、27.238 3,由此可见IPF准确性较好.
结合式(20)~(21),可得可靠度指标预测值和监测值如图13所示.可以看出,可靠度指标预测值较好反映了监测可靠度指标的变化趋势,而考虑了不确定性与随机性的可靠度指标预测值略低于实测值,但由于考虑了不确定性,预测值更符合工程实际.
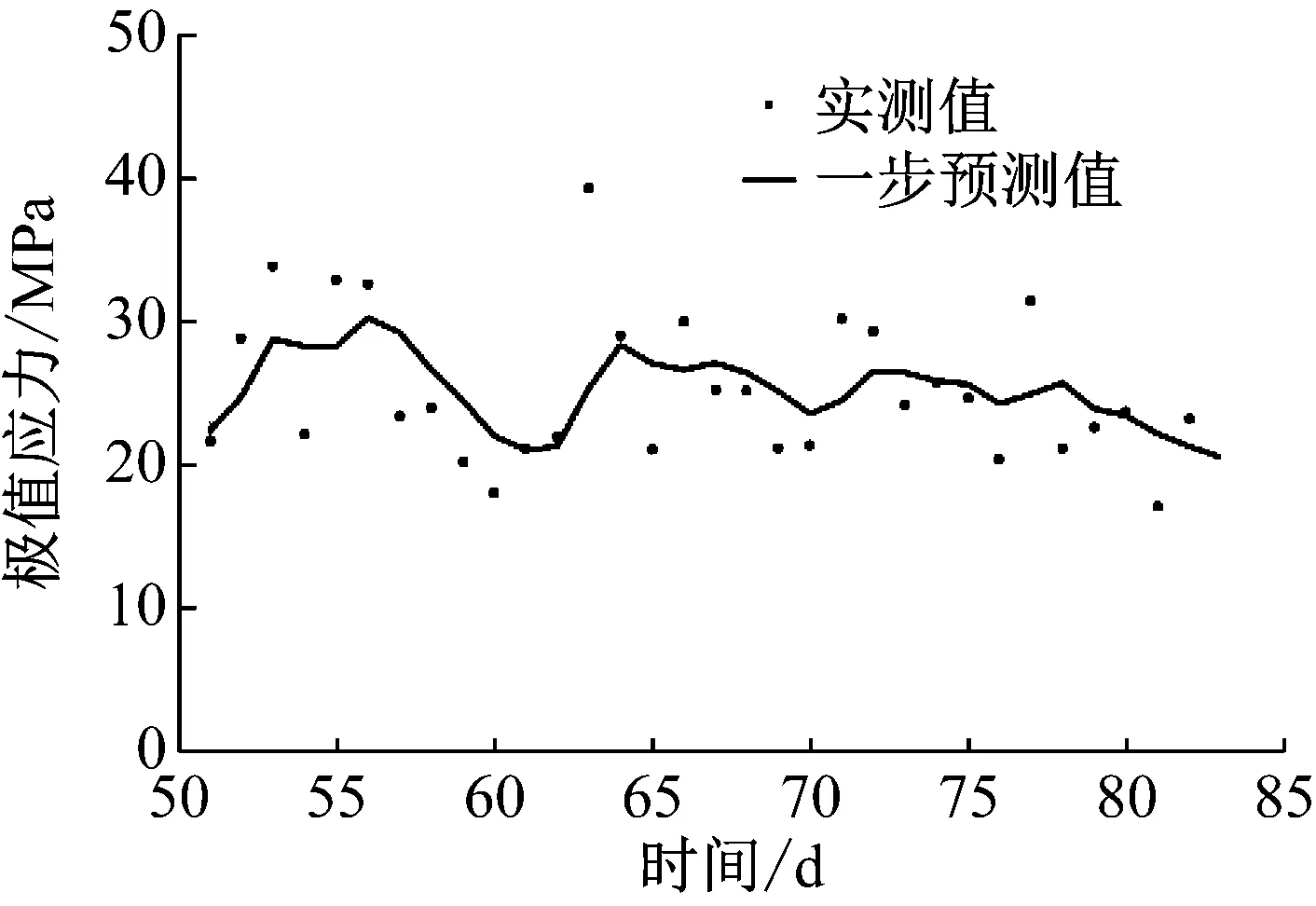
图11 基于改进粒子滤波器的极值应力预测值与实测值(工程实例2)
Fig.11 Monitored and predicted extreme stresses

图12 3种算法极值应力预测结果比较(工程实例2)

图13 可靠度指标的实测值与一步预测值(工程实例2)
4.3 工程实例3计算分析
采用吉林长春伊通河桥上游主梁70 h的极值挠度监测数据对所提算法进行验证.极值挠度数据如图14所示.
首先基于前50 h的监测极值挠度数据,结合式(1)~(3)建立动态模型如下:
状态方程为
Xt=Xt-1-0.049 5+wt,wt~N(0,Wt)
(30)
监测方程为
Zt=Xt+vt,vt~N(0,1.421 3)
(31)

图14 极值挠度监测值(工程实例3)
初始状态信息为
Xt-1|Dt-1~N(45.869 2,0.953 9)
(32)
然后采用所提IPF预测算法,结合式(7)~(15)与式(30)~(32),基于第50小时到第69小时的监测极值挠度信息,对第51小时到第70小时的极值挠度进行动态预测,预测结果如图15所示.并与PF[21]及 ARIMA[22]进行比较,预测结果对比如图16所示.利用式(15)得到IPF、PF以及ARIMA(1,0,2)的EMSE分别为0.907 6、1.628 3、1.427 7,由此可见IPF预测性能较好.

图15 基于改进粒子滤波器的极值挠度预测值与实测值(工程实例3)
Fig.15Monitored and predicted extreme deflections based on IPF

图16 3种算法极值挠度预测结果比较(工程实例3)
结合式(22)和式(23),可得可靠度指标分析结果如图17所示.可以看出可靠度指标预测值很好地反映了监测可靠度指标的变化趋势,而考虑了不确定性与随机性的可靠度指标预测值略低于实测值,但由于考虑了不确定性,预测结果更符合工程实际.

图17 可靠度指标的实测值与一步预测值(工程实例3)
4.4 桥梁环境突变的假设试验
由于桥梁的应力环境受外界因素影响较大,当在役桥梁气候条件、桥下水位等外在环境因素发生突变时,桥梁的应力状况会也会随之出现变化.假设4.1中富民桥在监测到第600小时候桥梁环境发生突变,例如受到洪水影响,现假定其实际监测信息受到如下变化:

(33)

现利用改进的粒子滤波算法,结合式(7)~(15)、式(24)~(26)以及式(33),基于第300小时到第809小时的监测极值应力数据,对第301小时到第810小时的监测极值应力进行实时动态一步预测,同时与PF方法结果进行对比,预测结果如图18所示.可以明显地看出,由于IPF的建议分布在更新过程中借助了突变后的应力信息,因此仍能产生较为合理的建议分布,有效地对突变后的监测信息进行预测,而PF算法由于粒子集合的分布不能很好地覆盖真实值,因此当监测信息突变时出现了难以避免的的滤波发散.
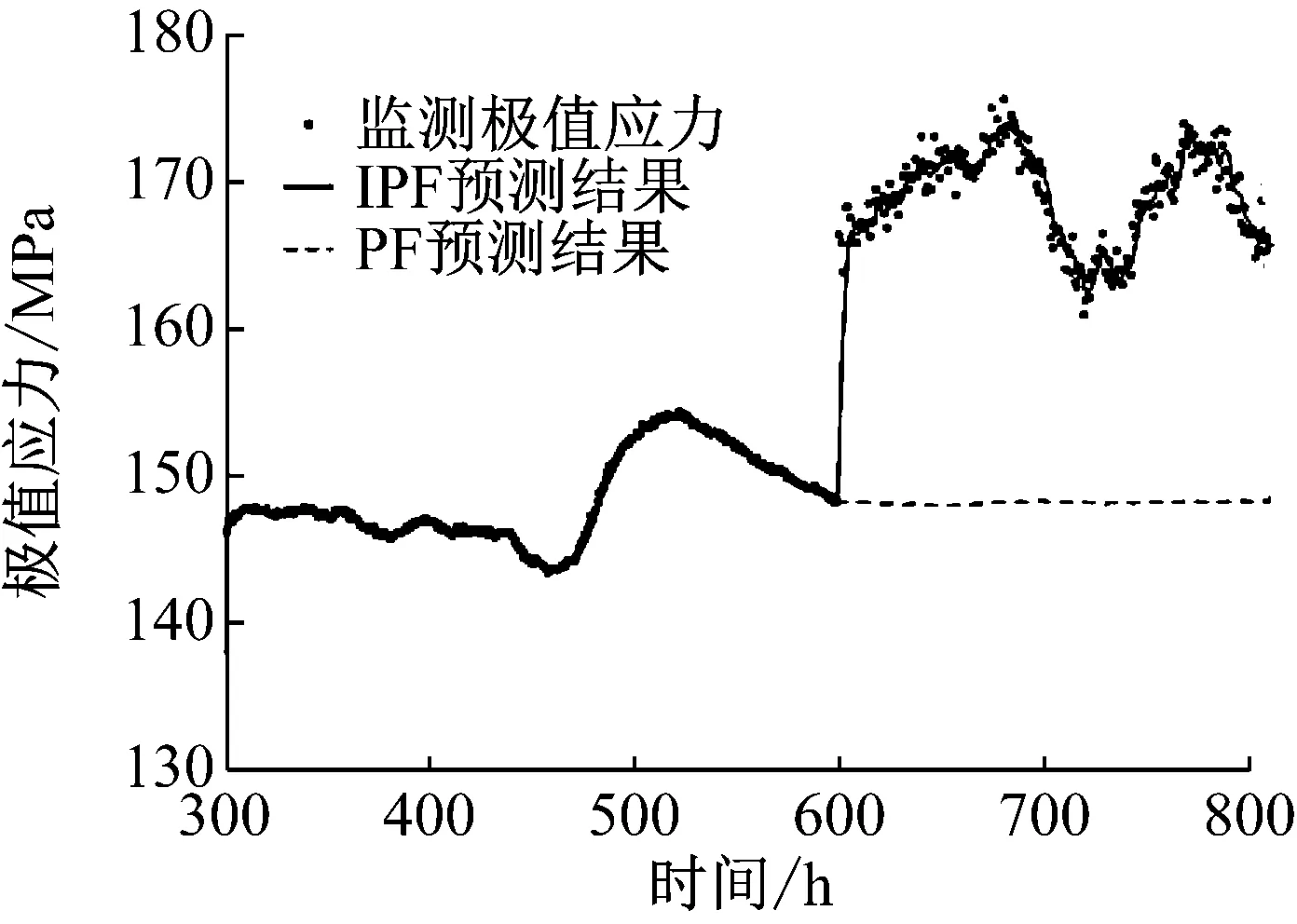
图18 桥梁环境突变下的应力预测结果
5 结论
提出了一种用于桥梁动态可靠度指标在线预测的改进粒子滤波算法.基于天津富民桥主缆、美国I-39北桥第二跨横桥以及伊通河桥上游主梁的监测数据对所提算法进行了验证分析,为证实算法的适用性和鲁棒性,进行了假设试验验证,通过假设试验可以模拟多种情况下桥梁极值应力(或挠度)的预测分析.
基于监测极值应力(或挠度)信息对极值应力(或挠度)进行了预测分析,预测结果与实测值变化趋势基本保持一致,预测结果的均方误差也较为理想,且通过对比发现改进的粒子滤波器预测精度十分可观;此外,在桥梁极端情况下,IPF的预测性能良好,具有良好的预测稳定性以及对突变数据的灵敏性与自适应性.而对桥梁结构可靠性进行预测分析时,可靠度指标的一步预测值与实测值标化趋势十分吻合,而考虑了随机性影响所得到的预测可靠度指标从整体上略微低于实测值,但更符合实际情况.
