多盘转子系统的振动失效灵敏度分析
2019-08-07苏长青李紫薇郭凡逸
苏长青,李紫薇,郭凡逸
(1.沈阳航空航天大学 安全工程学院, 沈阳 110136;2.辽宁省飞机火爆防控及可靠性适航技术重点实验室, 沈阳 110136)
转子是一种常见的旋转机器,它连同轴承与支座等统称为转子系统。汽轮机、发电机、电动机的核心工作部件都是转子。转子转动时,系统会发生振动并产生噪声,使转子系统的工作效率降低,严重时振动会导致转轴断裂,造成严重的事故[1]。
系统的频率可靠性问题的研究主要有两个方向,一是由强迫振动引起的系统响应超限;二是由于系统共振与非共振引起的结构疲劳[7]。文献[4]研究了具有独立失效模式的随机多自由度非线性系统的可靠性分析;文献[5]在强迫振动放大系数模型的基础上提出了离心叶轮叶片的振动可靠性分析方法;文献[6]以结构振动设计方法为基础,通过应力-干涉理论研究了一种振动可靠性分析办法;文献[7]研究了具有相关失效模式的转子系统频率可靠性的问题。
本文以三盘转子为研究对象,考虑了弹性支承与圆盘质量的随机特性,应用有限元法建立系统的振动方程,获得系统的前6阶固有频率的随机统计特性,建立了转子系统共振的状态函数,并应用Monte Carlo法分别计算出系统的可靠度与可靠性灵敏度[7]。
1 转子系统的固有频率与临界转速
对于转轴具有n个节点,且忽略轴承座的等效质量的转子系统,其位移向量为:
{U1}=[x1,θy1,x2,θy2…xyn-1,θyn-1]
{U2}=[y1,-θx1,y2,-θx2…yyn-1,-θxn-1]
(1)
由于滑动轴承的刚度系数相等,则系统的运动方程的齐次式为:
(2)
其中[M1],[C],[K1],都为2n×2n的对称稀疏带状矩阵。故其频率方程为:
|-M1ω2+J1Ωω+K1|=0
(3)
当转子以角速度Ω转动时,根据频率方程可求得2n个正进动频率与2n个反进动频率;当Ω=ω时,其值为系统的临界转速。
2 转子系统可靠度与失效灵敏度分析
2.1 转子系统可靠度计算
在结构可靠度分析中,结构的极限状态是通过结构的功能函数描述的。对于转子系统,其产生的共振会使未超过槛值的响应导致系统的失效或使系统处于失效的极限状态。根据可靠性理论,共振转子系统的状态函数为:
gi(n,ωi)=|n-ωi|i=1,2,…,k
(4)
式中,n为转速,即转子系统的激振频率;ωi为转子的第i阶固有频率。当gi>0时,转子系统处于可靠状态;当gi<0时,转子系统处于失效状态。
当转子系统的激振频率接近其某阶固有频率时,转子系统发生共振。根据此关系,将上式改写为:
(5)
其中γ为转子系统一阶固有频率的10%。
对于转子系统,只要有一个激振频率接近其某阶固有频率,则系统就会发生共振导致失效。故应把转子系统考虑为串联结构体系。此时转子系统的失效概率为:
(6)

(7)
式中,Pi为第i失效模式下的转子系统失效概率;Pf为转子系统联合失效概率;μn-ωi为固有频率均值与激振频率差的均值;σn-ωi为固有频率方差与激振频率差的标准差。
2.2 转子系统可靠性灵敏度计算
Monte Carlo法是最通用的、应用范围最广的计算可靠性灵敏度的数字模拟方法。此方法对于状态函数的形式与随机参数的分布情况没有特殊要求,主要是把求解可靠性灵敏度的复杂积分问题转换为求解数学期望问题,用样本均值来估计数学期望[8]。
转子系统失效灵敏度为失效概率Pf对随机参数xi的分布参数μxi、σxi的偏导数。
(8)
将式(8)中的积分变换成数学期望的表达式,之后就可以用Monte Carlo法来计算转子系统失效灵敏度。具体变换方法如下:
(9)
在用Monte Carlo法计算的过程中,采用样本均值来代替总体均值,则均值灵敏度计算公式为:

(10)
同理,可得到标准差灵敏度公式为:
(11)
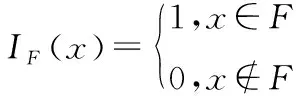
为了更好的比较不同分布参数对失效概率的影响程度,要消除基本变量量纲对失效灵敏度的影响。以均值灵敏度为例,其无量纲的灵敏度表达式为:
(12)
Sμxi的估计值为:

(13)
对于正态变量有:
(14)
式中,μi为对基本随机向量x=(x1,x2,x3,…,xn)T中的第i个分量xi引入的标准正态变量。
则除去量纲影响的均值失效灵敏度为:
(15)
同理可得去除量纲影响的标准差失效灵敏度为:
(16)
式中,μji为第j个样本xj=(xj1,xj2,xj3,…,xjn)的第i个分量xji所对应的标准正态化样本。
3 数值算例
转子系统结构简图如图1。轴承1与轴承3分别位于转轴的两侧,轴承2位于圆盘2与圆盘3之间。转子系统几何参数值如表1所示。

图1 转子系统结构简图

几何参数数值几何参数数值L/m1.474D3/m0.15d/m0.045B1/m0.02D1/m0.100B2/m0.02D2/m0.225B3/m0.03
由于制造环境、技术条件、制造和安装误差及材料的多相特征等因素使得圆盘质量、轴承刚度与阻尼具有一定的随机特性[9]。本文中把上述参数作为随机参数,一般来讲,结构的质量、刚度和阻尼服从正态分布,如果随机参数服从非正态分布,可将非正态分布转化为正态分布处理。如果其具体的分布如表2所示。转子系统的前6阶固有频率为随机输出参数,其具体的分布如表3所示。
抽样方法本文选用重要度抽样法(importance sampling method)。通过改变随机抽样的中心,使样本点有较大概率处于失效域内。为了使Monte Carlo法的计算结果达到较高的精度要求,本文取抽样次数为500次进行循环仿真,分析了在不同的激振频率(服从正态分布)下,转子系统的可靠度。其结果如表4所示。
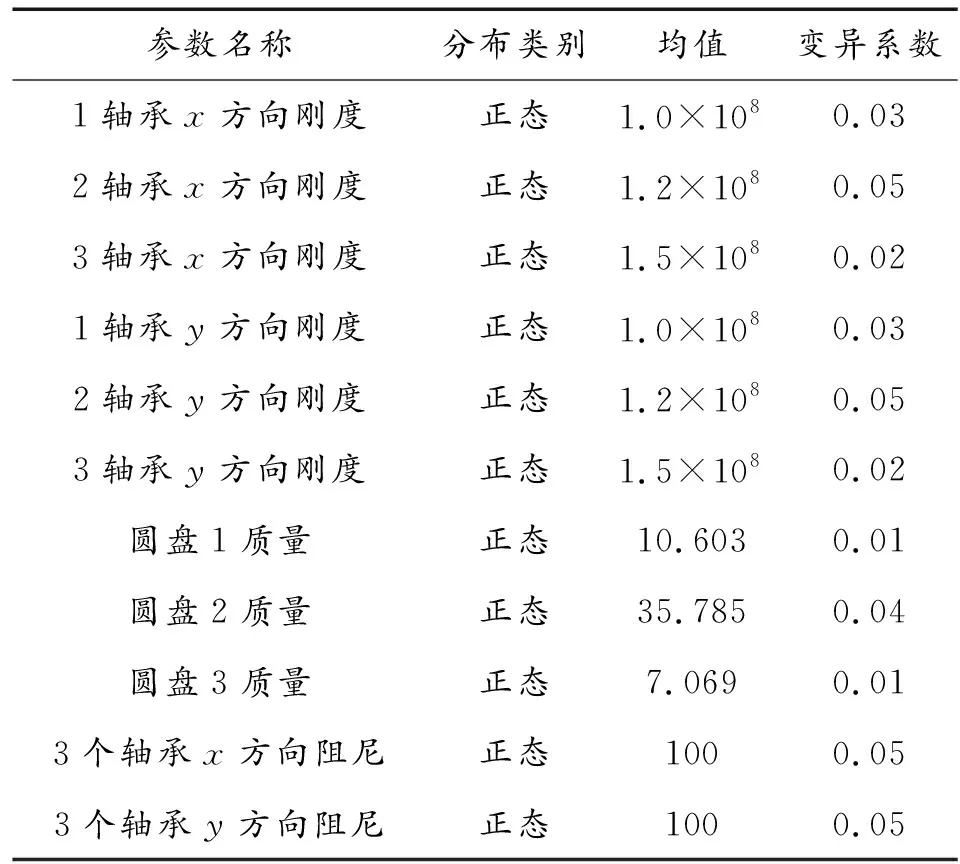
表2 转子系统随机参数统计特性
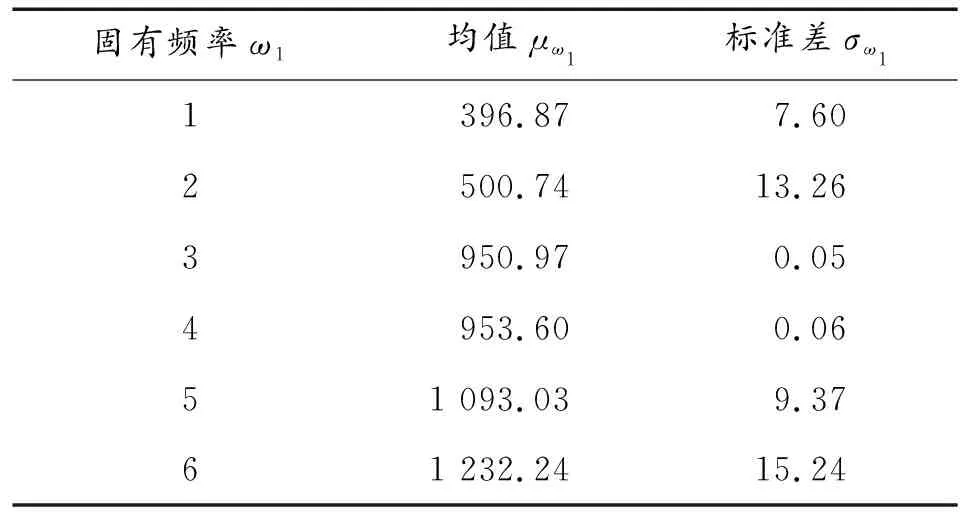
表3 转子系统固有频率随机特性
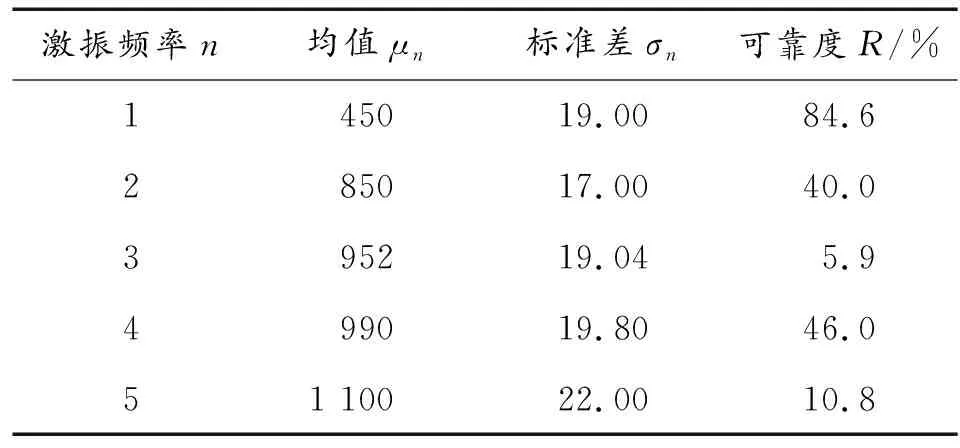
表4 转子系统可靠度
其中450 rad/s这一激振频率处于1阶与2阶固有频率之间,距离两固有频率分布都较远,系统发生共振的概率较低,所以转子系统的可靠度较高;而952 rad/s与1 100 rad/s这两激振频率分别距离4阶固有频率与6阶固有频率非常近,系统发生共振的概率较高,所以转子系统的可靠度较低。
转子系统在不同激振频率下的各参数失效灵敏度如图2~图6所示。
由于在952 rad/s这一激振频率下,转子系统的可靠性最低,所以分析此状态下的各参数灵敏度显得十分重要。如图4所示,2轴承y方向刚度方差灵敏度与1轴承x方向刚度均值灵敏度值最大且为正,而圆盘2质量方差灵敏度也较大且为负,故想在此工作状态下提高转子系统的可靠度应增大2轴承y方向刚度方差与1轴承x方向刚度均值,同时要减小圆盘2质量方差。
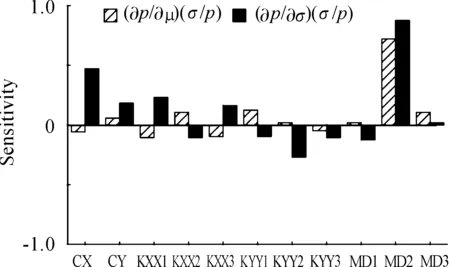
图2 450 rad/s下转子系统各参数失效灵敏度
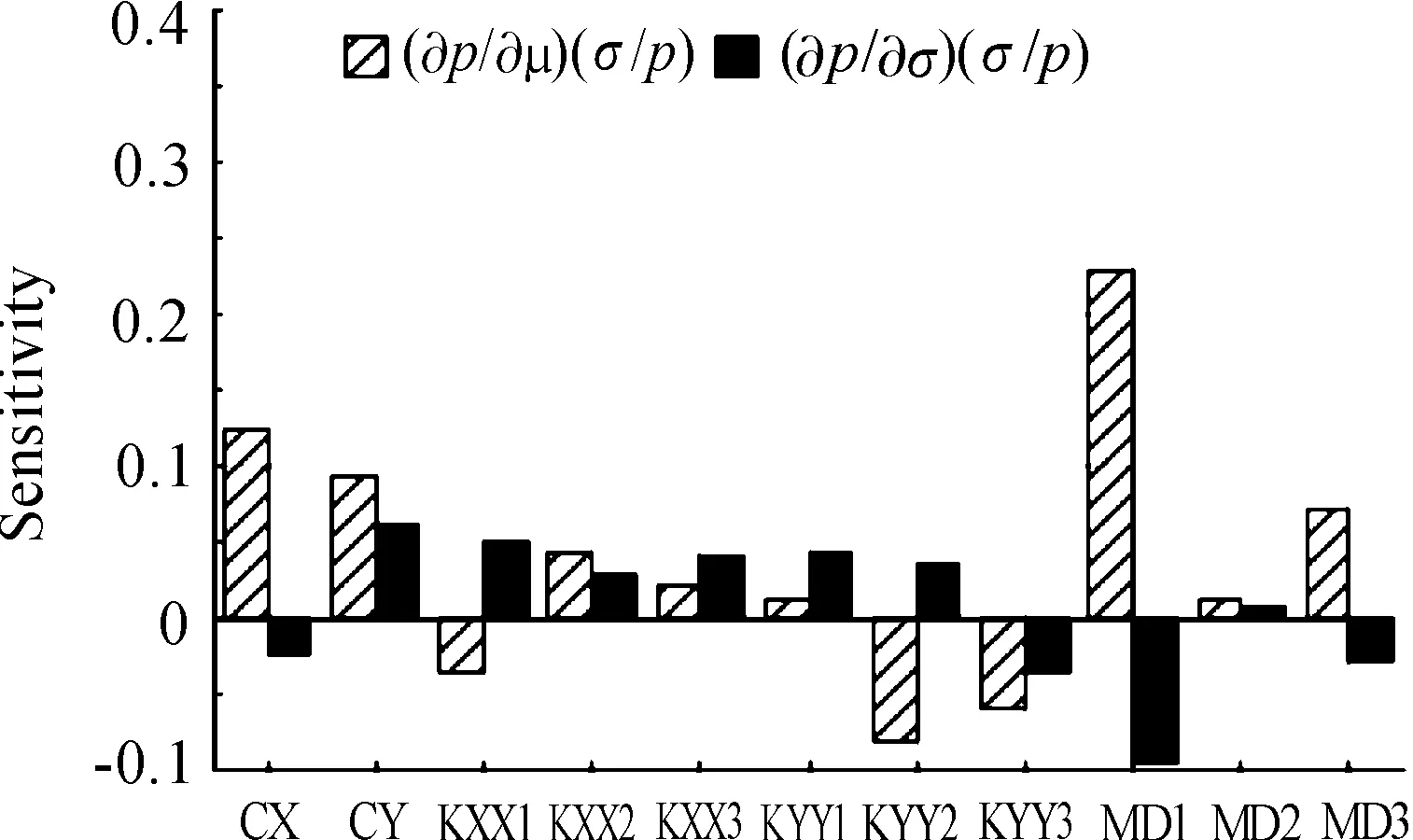
图3 850 rad/s下转子系统各参数失效灵敏度
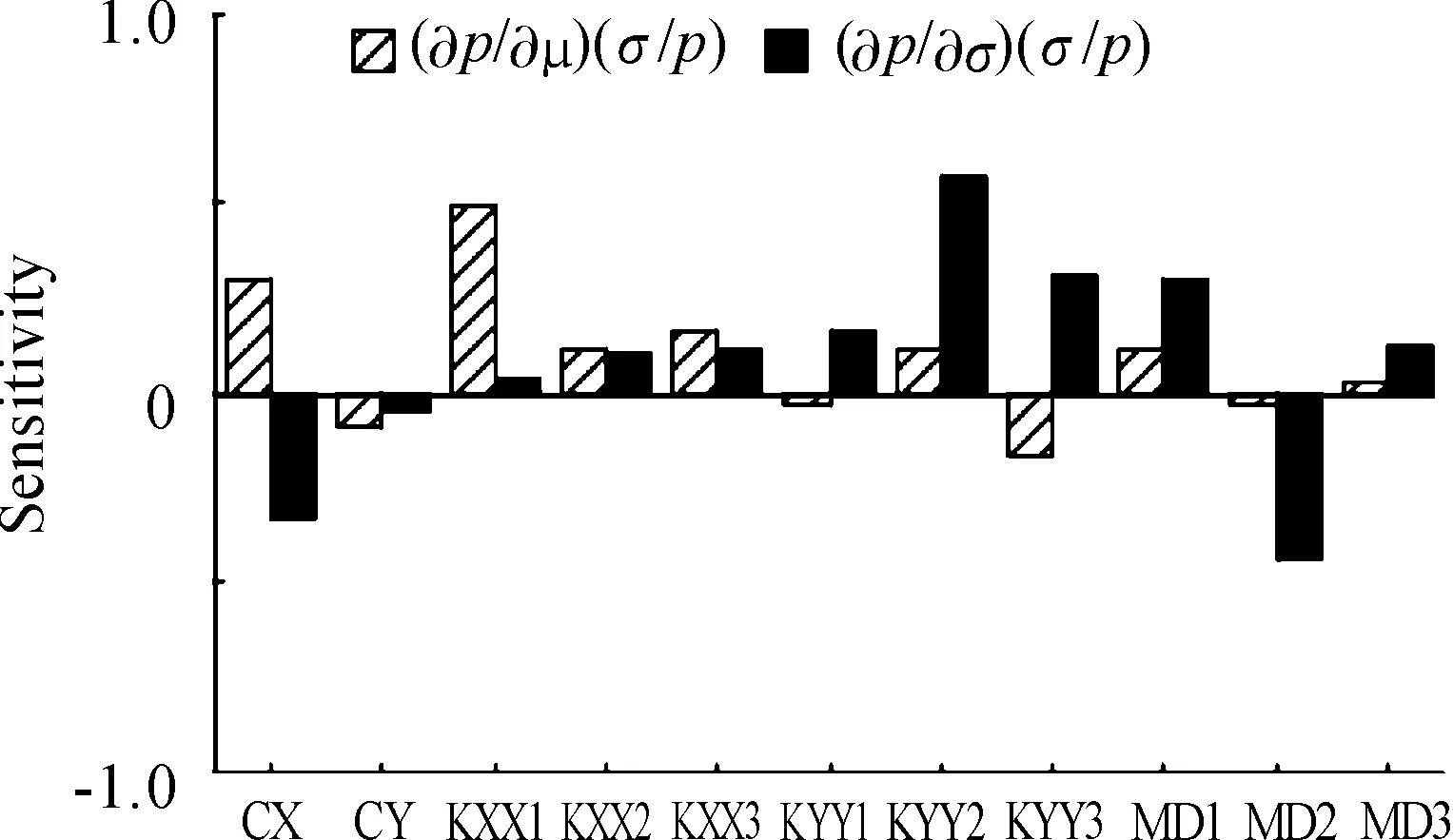
图4 952 rad/s下转子系统各参数失效灵敏度
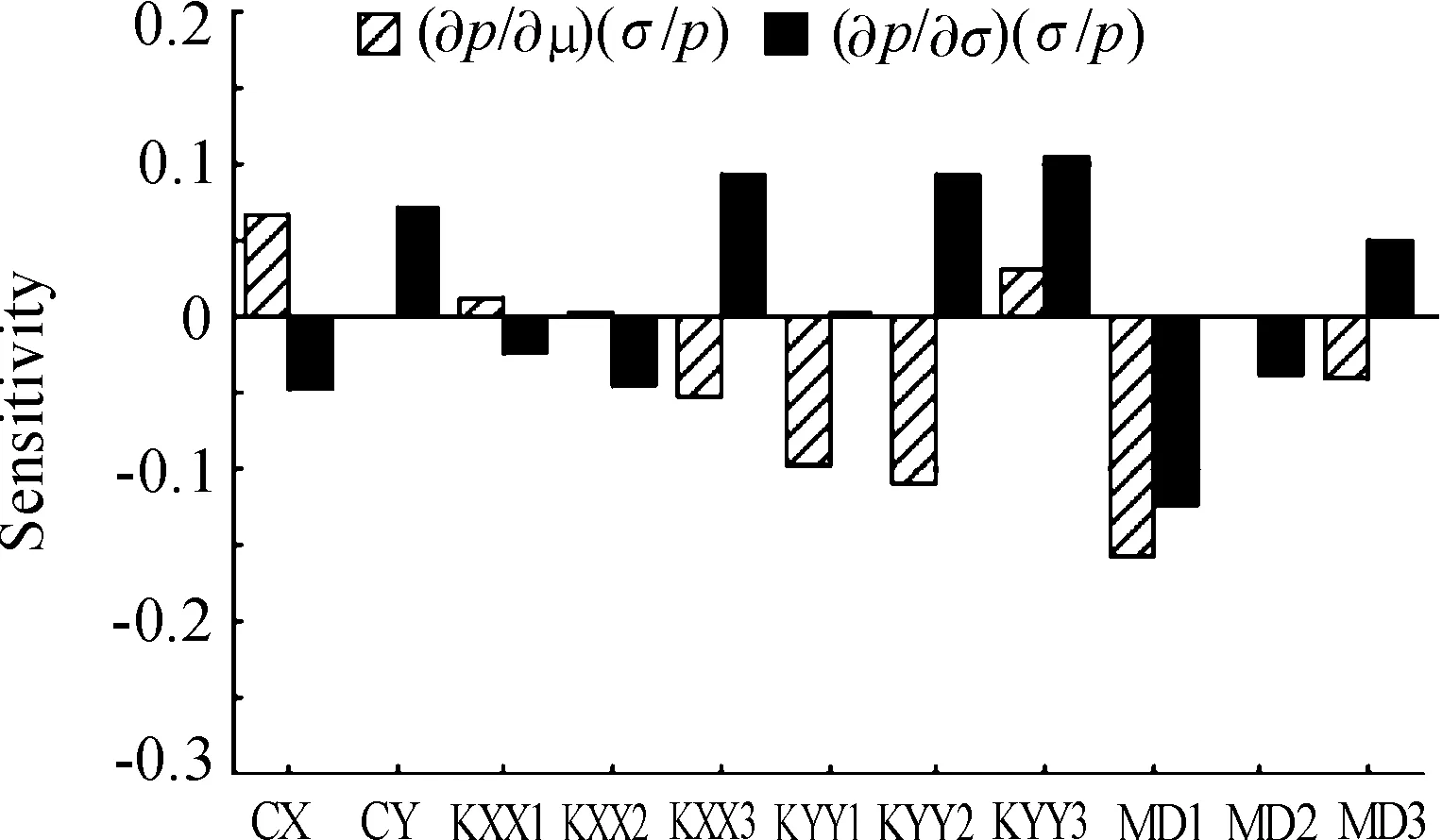
图5 990 rad/s下转子系统各参数失效灵敏度

图6 1 100 rad/s下转子系统各参数失效灵敏度
4 结论
本文以多盘转子系统为研究对象,基于共振失效的基本准则,建立了多盘转子系统的振动可靠性模型,提出了多盘转子系统的振动失效灵敏度分析方法,研究了随机参数统计特性对于系统失效的影响规律,研究成果能够为转子系统的设计、制造和结构优化提供一定的理论依据。
