电厂管道90°弯头流动加速腐蚀的模拟研究

林 彤，周克毅，司晓东

(东南大学 能源与环境学院，南京 210096)

流动加速腐蚀(FAC)是在流动条件下，流体加速管道表面的氧化膜溶解在流动的水或湿蒸汽的过程，随着管壁表面的氧化膜减薄，使金属基体逐渐暴露于介质中，情况严重时会导致管道破裂，FAC是火电厂和核电厂管道最常见的失效原因[1]。近几十年来，发生了多起由于FAC引发的管道泄漏事故[2-4]，造成严重的人员伤亡和巨大的经济损失，严重威胁电厂的安全运行[5]。随着我国超超临界机组发展迅速，机组运行也逐渐暴露出一系列问题，如锅炉压差上升较快、结垢速率高、汽轮机高压缸部位沉积严重等，根本原因是普遍存在FAC现象[6]。

FAC发生条件多为高温、高压、高流速，若要进行试验需要大量的经费，采用计算机模拟耗时少、灵活性高、可重复性强。利用流体力学计算软件，可以确定管道内部的流速、压力分布，对于预测FAC发生部位有一定的意义[7]，并且FAC发生处多为弯头、孔板和异径管等流场变化剧烈的部位[8]。因此，笔者利用ANSYS软件来研究电厂90°弯头处FAC的规律，为类似问题提供指导。

1 FAC机理

由于边界层的存在，电厂管道中的流体靠近氧化膜的流速较低、远离边界层的流速较高。主流中可溶性含铁组分的浓度很低，边界层中的含铁组分会向主流方向迁移，使边界层处含铁组分减少，最终导致靠近边界层的氧化膜以一定速率溶解。氧化膜内层结构致密，外层结构疏松，金属基体生成的可溶性含铁组分通过氧化膜的孔隙扩散到边界层，造成含铁组分从金属基体向主流区的迁移，而主流区的高速流体不断将含铁组分带走，造成碳钢表面的持续腐蚀。FAC过程与静止腐蚀相比，主要区别在于氧化膜-溶液界面上流体速度的影响，因此FAC可以分为传质和电化学的耦合过程[9]。具体电化学反应过程见图1[8]。

图1 FAC机理图

FAC是可溶性的含铁组分由于浓度差的作用被主流带走的过程。首先，在金属氧化物界面上，金属基体与H+发生反应生成Fe2+；其次，由于从金属基体和主流区间的浓度差，一部分Fe2+运动到氧化膜附近。与氧化膜-溶液界面处Fe2+的浓度相比，水溶液中Fe2+的浓度非常低，在浓度差作用下，氧化物-溶液处的Fe2+向主区流扩散，此时流体不断流动，带走主流区Fe2+，扩散过程持续进行，导致壁厚持续变薄。FAC反应速率可表示为：

(1)

式中：KFAC为流动加速腐蚀速率，m/s；ceq为可溶性含铁组分的溶解度，mol/L；c∞为主体溶液中可溶性含铁组分的浓度，mol/L；K为反应速率常数，m/s；k为传质系数，m/s；f为由金属基体附近扩散到外部的溶解铁的比例系数；δ为氧化膜厚度，m；n为氧化膜孔隙率；D为可溶性含铁组分的扩散系数，m2/s。

Berge认为有大约一半含量的铁直接扩散到主体溶液中[10]，即f=0.5。由于主体溶液中含铁组分的浓度相较于含铁组分的溶解度非常小，则可假定c∞=0，则方程变为：

(2)

2 计算模型

2.1 溶解度的计算

氧化膜内层结构致密，外层结构疏松，微溶于水。Fe3O4在高温下与水溶液存在多个化学反应，反应生成物也各不相同。FUJIWARA K等[1]的研究表明溶液的溶氧量很低且其pH小于10时，Fe3+浓度非常低，所以氧化膜的溶解方程一般为：

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

式中：K0、K1、K2、K3分别为式(3)、(5)、(7)、(9)的反应平衡常数。

磁性氧化铁的溶解度为：

ceq=c[Fe2+]+c[Fe(OH)+]+

=c[H2]1/3(K010-2pH+K110-pH+

K2+K310pH)

(11)

温度会影响化学反应速率，Ki均与温度有关，其拟合公式为：

lnKi=[-Ai/T+Bi(lnT-1)+Di)]/R

(12)

式中：T为热力学温度，K；R是理想气体常数，R=8.314 J/(mol·K)；Ai、Bi和Di为常数，其值见表1[11]。

表1 常数Ai、Bi和Di的值

2.2 传质系数的计算

传质系数受流场分布的影响，须得知90°弯头的流场分布情况。遵循质量守恒、动量守恒和能量守恒，利用ANSYS软件模拟得到弯头内的速度分布，基于流体速度和传质系数的关系求得传质系数。模拟采用假设为：忽略重力的影响；流体介质不可压缩；不考虑管子的散热。

控制方程为：

(13)

(14)

(15)

式中：ρ为流体密度，kg/m3；u为流体速度，m/s；t为时间，s；μ为动力黏度，Pa·s；ui、uj分别为x、y轴方向上的速度分量，m/s；xi、xj分别为x、y轴方向上的坐标分量；Suj和ST分别为动量源项和能量源项；λ为热导率，W/(m·K)；cp为比定压热容，J/(kg·K)。

传质系数和流体速度之间存在如下关系[1,12]：

k=a(ρdu/μ)b(μ/D)c(D/d)

(16)

D=kBT/(6πμdM)

式中：a、b、c为常数；d为管道当量直径，m；D为分子扩散系数，m2/s；kB为玻尔兹曼常数；dM为溶液中的离子半径，m。

3 结果与分析

3.1 溶解度的计算结果

在调查的所有火电厂中，其中有60%的火电厂都在给水加热器疏水系统发生过FAC[8]。以疏水部位的压力和温度作为参考，结合FAC高发的温度区间范围，将流体的温度、压力设定为150 ℃、2 MPa；电厂水侧管道流速普遍在2～6 m/s，流体流速设定为3 m/s；pH随着温度改变，常温(25 ℃)时pH为9.40，150 ℃时pH为6.86[13]。Berge等通过测量得出H2浓度在7.8×10-4～3.25×10-3mol/L，H2浓度取1.5×10-3mol/L[14]；根据T=423.15 K计算得到反应平衡常数K0、K1、K2、K3(见表1)；最终计算得到可溶性含铁组分的浓度为6.477×10-8mol/L。

3.2 流场模拟结果

笔者建立的90°弯头的三维数值计算模型见图2。

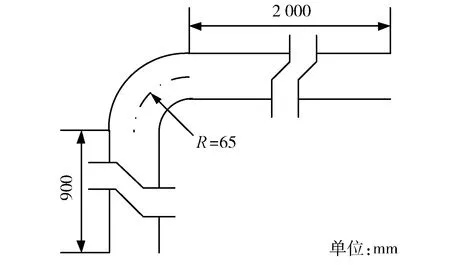
图2 90°弯头的三维数值计算模型

为了保证实验段流体流动达到充分发展的状态，同时实验段出口流体流动不对实验段造成影响，实验段入口长度取为2 000 mm，出口长度取为900 mm。绘制几何模型并将模型导入ICEM控件，利用O形网格剖分对90°弯头进行划分，构建结构网格，并且对模型的边界层进行加密处理，共构建694 783个网格，对结构网格进行质量检验，得到网格质量在0.65～1.00，符合计算要求。将划分好的网格导入FLUENT软件，采用Pressure-Based求解器，使用Realizablek-ε模型，选用SIMPLE压强-速度关联算法，采用二阶迎风差分格式，保持松弛因子默认设置，对建立的模型进行了数值计算。管内工质流速设定为3 m/s，管内直径设定为50 mm，实验段入口边界条件为速度入口，实验段出口边界条件设置为压力边界(2.026 5×106Pa)，工作流体为液态水，密度为917.87 kg/m3，黏度为1.83×10-4Pa·s，特性为不可压缩流体。湍流强度的设置参照下式[15]：

(17)

式中：I为湍流强度；Re为雷诺数。

经过计算可得I为2.948%。

笔者将90°弯头模型进行了区域划分，沿流动方向共分为9个区域，每隔10°进行划分，由于管道轴对称，沿管道径向方向则划分为0°、42°、138°、180°，φ=0°为内弯侧，φ=180°为外弯侧，具体见图3。

图3 90°弯头模型的区域划分

图4分别给出了流体速度为3 m/s，θ=0°、20°、50°、70°、90°时管道截面的流场分布。在弯头内弯侧流体速度沿流动方向逐渐增大，随后不断减小，在外弯侧流体速度沿流动方向逐渐增大，直至与主流汇合。主流区域由于惯性的影响保持向前流动的趋势，由于弯头的阻碍不得不偏转方向流动，主流区整体偏移，离开弯头后流场逐渐趋于稳定。

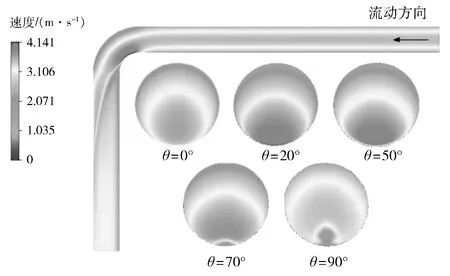
图4 不同θ下的圆管界面流速分布

在10个圆截面上各取4个点，分别为φ=0°、42°、138°、180°，流体速度分布见图5，弯管内最大速度和最小速度都在内弯侧，分别为3.8 m/s和0.505 m/s。内弯侧流体速度从弯管入口处开始逐渐增大，到θ=20°左右达到峰值，然而内弯侧由于发生二次流产生漩涡，消耗内弯侧流体的能量，使得内弯侧速度迅速下降。在φ=42°处，流体刚进入弯管，速度逐渐增大，随着漩涡的出现，速度有下降趋势，主流区从内侧向外侧偏移的过程中，经过φ=42°处，使得速度重新增大，当主流区已偏移到弯头外侧时，漩涡作用使速度继续减小。弯管内其他部位由于距离漩涡较远，受到影响较小，速度基本不变。流体继续在弯管内流动，主流区向外侧偏移，使得外弯侧及靠近外弯侧的速度逐渐增大到弯管出口均达到最大值。

图5 90°弯头内各点的速度

3.3 传质系数的计算结果

图6为90°弯头内各点的传质系数。随着流体速度的增加，使流场内的湍流强度增大，流体间的运动增强，使得动量输送和热传递变得频繁，传质过程增强，从而使传质系数增大。

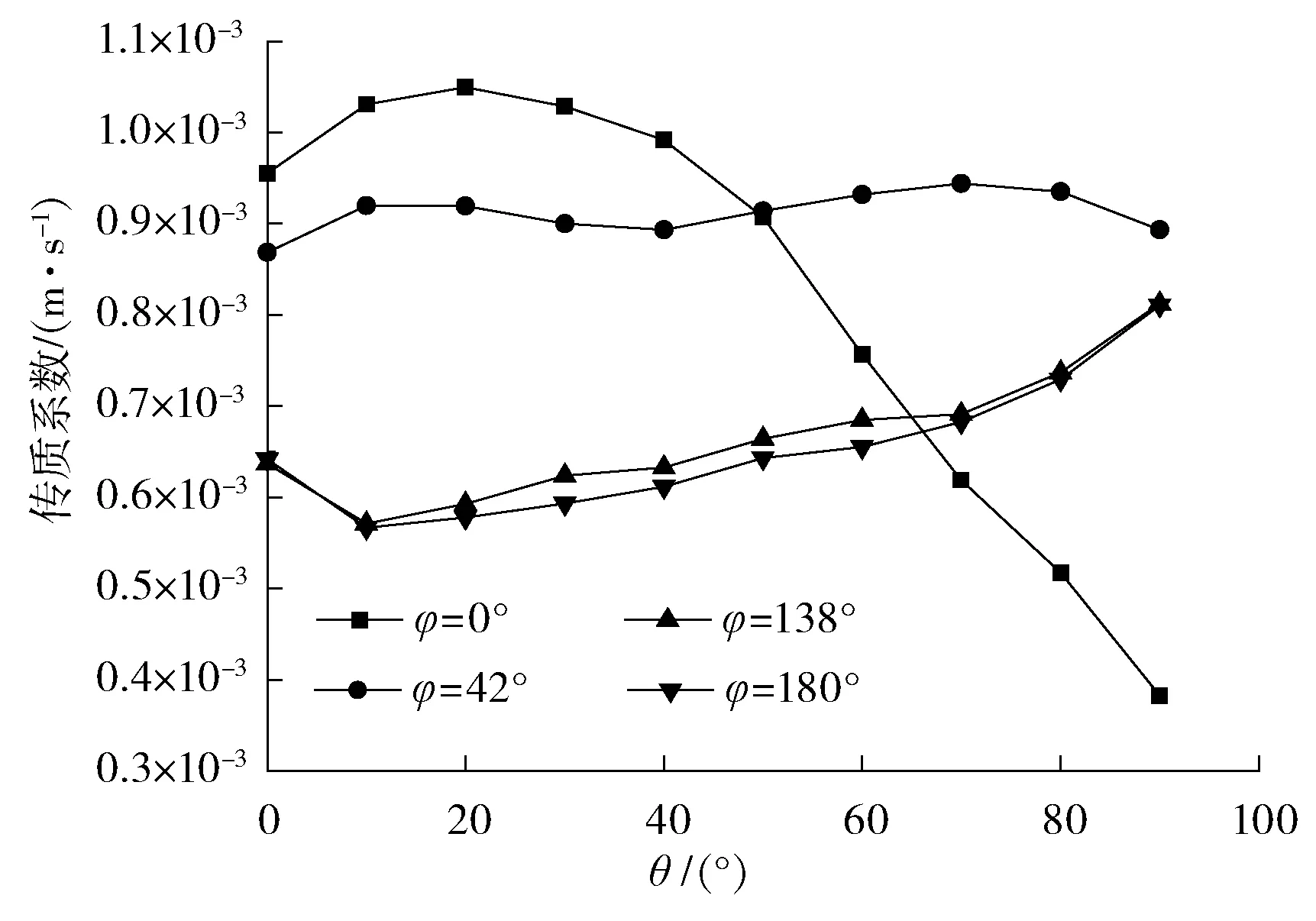
图6 90°弯头内各点的传质系数

由图5和图6可得：传质系数和速度的趋势基本相同，随着流体速度增加，传质系数增大，与速度分布一致。沿着管道径向方向，从内弯侧到外弯侧传质系数整体呈现下降趋势，内弯侧的传质系数达到最大值，外弯侧的传质系数整体较小。由于二次流的影响，内弯侧的传质系数急剧下降，在弯头的出口达到最小值。

3.4 腐蚀速率的计算

反应速率常数和温度满足阿伦尼乌斯公式[13]：

K=A·exp(-E/RT)

(18)

式中：A为指前因子；E为表观活化能，J/mol。

代入T=423.15 K，可求得K。经过上述计算，传质系数在10-4～10-3m/s，对反应的影响远大于反应速率常数，可将反应速率常数这一项忽略，简化计算过程。

氧化膜厚度和孔隙率并不是固定的值，会随着外界因素变化而改变。SANCHEZ-CALDERA L E等[16]发现当温度高于120 ℃时，孔隙率会随着温度的增加而减小，并且给出了实验数据，数据表明：当温度接近150 ℃时，孔隙率为0.005，氧化膜厚度为10-6m；当温度高于150 ℃时，氧化膜厚度主要与流体速度和pH有关。氧化膜厚度满足以下关系式[15]：

(19)

式中：α为常数；pH为8～10。

图7显示了温度为150 ℃、流体速度为3 m/s时，90°弯头内各处的FAC速率。

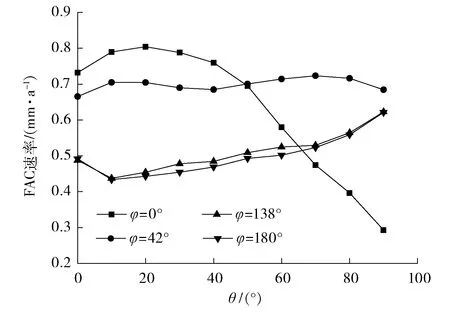
图7 90°弯头内各点的FAC速率

FAC速率和各点速度的变化趋势基本一致，速度越大，该处的FAC速率越大。为了确定理论计算结果的准确性，利用上述数学方程，通过模拟过程，计算得到t=25 ℃、pH为9.4、流体速度为3 m/s时的理论计算结果，并与ZHANG G A等[17]的实验结果对比(见图8)：沿着管道径向方向，对于φ=0°时，ZHANG G A等的计算结果与笔者计算结果很接近；对于φ=180°的数据，两者FAC速率变化趋势基本一致，进入弯管，FAC速率略有减小，随后一直保持增大的趋势；沿流动方向，例如θ=45°时，此时内弯侧的FAC速率最大，FAC速率从内弯侧到外弯侧逐渐减小，外弯侧的FAC速率最小，两者趋势依旧基本一致。

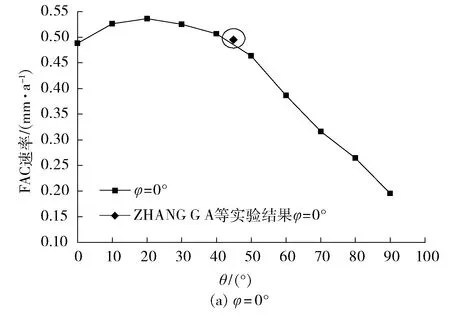
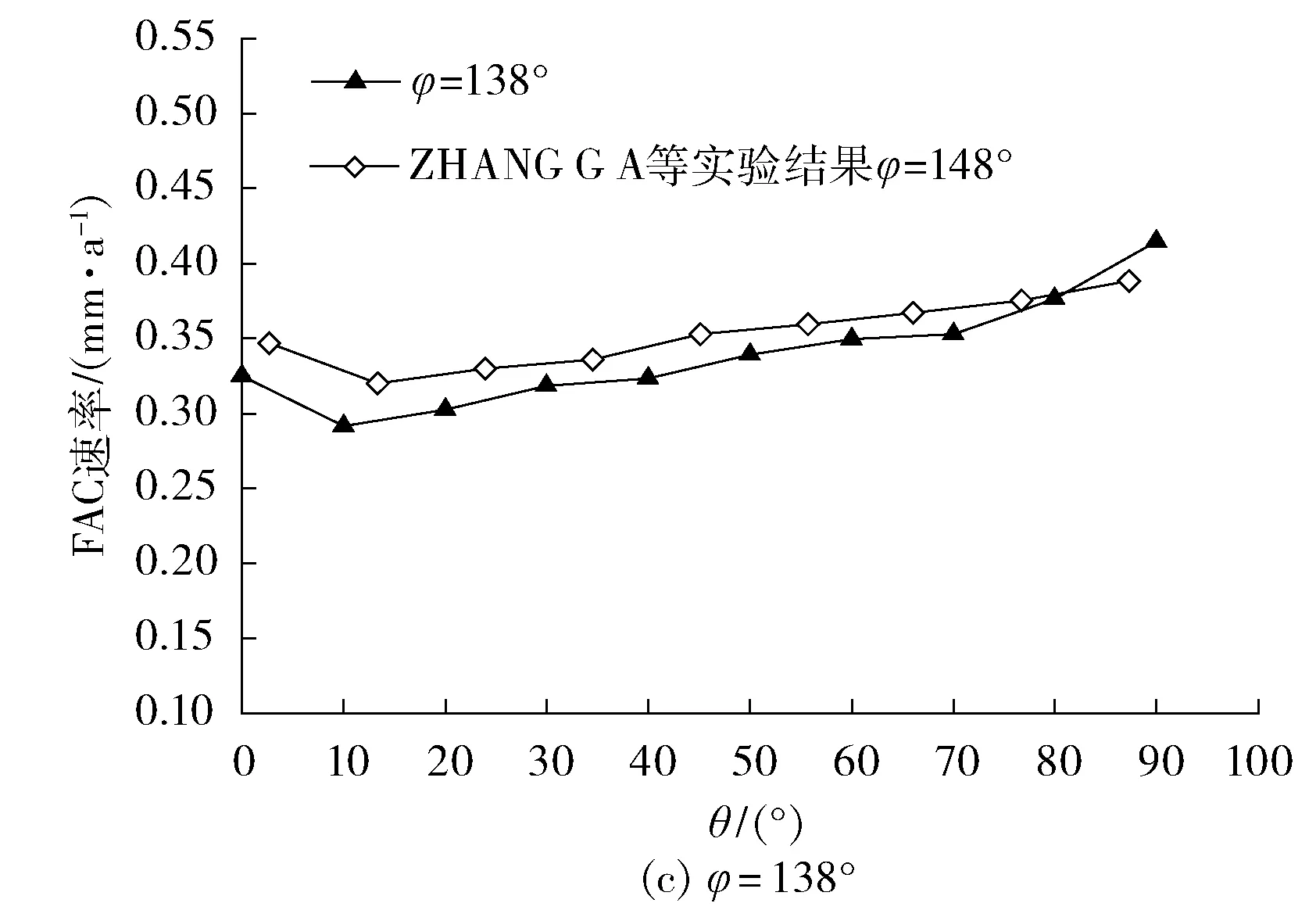
图8 模拟结果与实验结果对比

内弯侧的腐蚀速率沿着流动方向减小，但是对于90°弯头，腐蚀速率最大出现在内弯侧，说明在电厂管道运行过程中，弯头内侧某处FAC程度最为严重，管子的壁厚最薄，此处管子破裂的风险最大。基于模拟结果，电厂需要对90°弯头的内弯侧加强监控和监测，及时更换弯头。

4 结语

笔者研究了电厂90°弯头的流场分布情况，根据模型计算FAC过程中的传质系数与FAC速率，基于计算结果得到如下结论：

(1)流体刚进入弯头，速度逐渐增大，到θ=20°左右达到峰值，由于内侧发生二次流产生漩涡，使得内侧速度迅速下降。除去弯头内侧附近区域，沿着管道径向方向，流体速度从内弯侧到外弯侧逐渐减小，沿着流体流动方向，流体速度逐渐增大。

(2)90°弯头内部各处传质系数的情况与速度分布的情况基本保持一致，流体速度越大，流场内的湍流强度越大，传质系数也越大。

(3)在90°弯头内部，流体速度对FAC速率影响较大，流体速度越大，FAC速率越大。基于计算结果，最大FAC速率在内弯侧，FAC速率最小在外弯侧。