Global phase diagram of a spin-orbit-coupled Kondo lattice model on the honeycomb lattice∗

2019-08-06XinLi李欣RongYu俞榕andQimiaoSi

Chinese Physics B 2019年7期

关键词：李欣

Xin Li(李欣), Rong Yu(俞榕), and Qimiao Si

1Beijing National Laboratory for Condensed Matter Physics and Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

2School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China

3Department of Physics and Beijing Key Laboratory of Opto-electronic Functional Materials and Micro-nano Devices,

Renmin University of China,Beijing 100872,China

4Department of Physics&Astronomy,Rice Center for Quantum Materials,Rice University,Houston,Texas 77005,USA

Keywords: heavy fermion system,Kondo insulator,spin-orbit coupling

1. Introduction

Exploring novel quantum phases and the associated phase transitions in systems with strong electron correlations is a major subject of contemporary condensed matter physics.[1-3]In this context, heavy fermion (HF) compounds play a crucial role.[3-7]In these materials, the coexisted itinerant electrons and local magnetic moments (from localized f electrons) interact via the antiferromagnetic exchange coupling, resulting in the famous Kondo effect.[8]Meanwhile, the Ruderman-Kittel-Kasuya-Yosida (RKKY) interaction, namely the exchange coupling among the local moments mediated by the itinerant electrons, competes with the Kondo effect.[9]This competition gives rise to a rich phase diagram with an antiferromagnetic (AFM) quantum critical point (QCP) and various emergent phases nearby.[3,10]

In the HF metals,experiments[11,12]have provided strong evidence for local quantum criticality,[13,14]which is characterized by the beyond-Landau physics of Kondo destruction at the AFM QCP. Across this local QCP, the Fermi surface jumps from large in the paramagnetic HF liquid phase to small in the AFM phase with Kondo destruction. A natural question arises: how does this local QCP connect to the conventional spin density wave(SDW)QCP described by the Hertz-Millis theory?[15,16]A proposed global phase diagram[17-20]makes this connection via the tuning of the quantum fluctuations in the local-moment magnetism. Besides the HF metals,it is also interesting to know whether a similar global phase diagram can be realized in Kondo insulators(KIs),where the chemical potential is inside the Kondo hybridization gap when the electron filling is commensurate. The KIs are band insulators where the band gap originates from nontrivial strong electron-correlation effects. A Kondo-destruction transition is expected to accompany the closure of the band gap. The question that remains open is: do the local moments immediately order or do they form a different type of magnetic state,such as spin liquid or valence bond solid(VBS),when the Kondodestruction takes place?

Recent years have seen extensive studies about the effect of a fine spin-orbit coupling(SOC)on the electronic bands.In topological insulators(TIs),the bulk band gap opens due to a non-zero SOC,and there exist gapless surface states.The nontrivial topology of the band structure is protected by the time reversal symmetry(TRS).Even for a system with broken TRS,the conservation of combination of TRS and translational symmetry can give rise to a topological antiferromagnetic insulator(T-AFMI).[21]In general,these TIs and TAFIs can be tuned to topologically trivial insulators via topological quantum phase transitions. But how the strong electron correlations influence the properties of these symmetry dictated topological phases and the related phase transitions is still under active discussion.

The SOC also has important effects in HF materials.[20]For example, the SOC can produce a topologically nontrivial band structure and induce exotic Kondo physics.[22,23]It may give rise to a topological Kondo insulator(TKI),[24]which has been invoked to understand the resistivity plateau of the heavyfermion SmB6at low temperatures.[25]

From a more general perspective, the SOC provides an additional tuning parameter enriching the global phase diagram of the HF systems.[20,26]Whether and how the topological nontrivial quantum phases can emerge in this phase diagram is a timely issue. Recent studies have advanced a Weyl-Kondo semimetal phase.[27]The new heavy fermion compound Ce3Bi4Pd3displays thermodynamic[28]and zerofield Hall transport[29]properties that provide evidence for the salient features of the Weyl-Kondo semimetal. These measurements probe the linearly dispersing electronic excitations with a velocity that is renormalized by several orders of magnitude and singularities in the Berry-curvature distribution.

Theoretical studies are also of interest for a Kondo lattice model defined on a honeycomb lattice,[30]which readily accommodates the SOC.[31]In the diluted carrier limit, this model supports a nontrivial Dirac-Kondo semimetal(DKSM)phase,which can be tuned to a TKI by increasing the SOC.[32]In Ref. [30], it was shown that, at half-filling, increasing the Kondo coupling induces a direct transition from a TI to a KI.A related model,with the conduction-electron part of the Hamiltonian described by a Haldane model[33]on the honeycomb lattice,was subsequently studied.[34]

Here we investigate the global phase diagram of a spinorbit-coupled Kondo lattice model on the honeycomb lattice at half-filling. We show that the competing interactions in this model give rise to a very rich phase diagram containing a TI,a KI, and two AFM phases. We focus on discussing the influence of magnetic frustration on the phase diagram. In the TI,the local moments develop a VBS order. In the two AFM phases, the moments are ordered, respectively, in the plane of the honeycomb lattice(denoted as AFMxy)and perpendicular to the plane (AFMz). Particularly in the AFMzphase,the conduction electrons may have a topologically nontrivial band structure, although the TRS is explicitly broken. This T-AFMzstate connects to the trivial AFMzphase via a topological phase transition as the SOC is reduced.

The remainder of the paper is organized as follows. We start by introducing the model and our theoretical procedure in Section 2. In Section 3,we discuss the magnetic phase diagram of the Heisenberg model for the local moments.Next,we obtain the global phase diagram of the full model in Section 4.In Section 5,we examine the nature of the conduction-electron band structures in the AFM states,with a focus on their topological characters. We discuss the implications of our results in Section 6.

2. Model and method

The model that we consider here is defined on an effective double-layer honeycomb lattice. The top layer contains conduction electrons realizing the Kane-Mele Hamiltonian.[31]The conduction electrons are Kondo coupled(i.e.,via AF exchange coupling JK)to the localized magnetic moments in the bottom layer. The local moments interact among themselves through direct exchange interaction,as well as the conduction electron mediated RKKY interaction; the interactions are described by a simple J1-J2model. Both the conduction bands and the localized bands are half-filled. This Kondo-lattice Hamiltonian takes the following form on the honeycomb lattice:

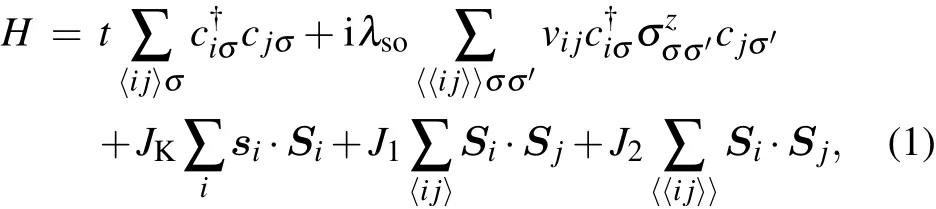
We use the spinon representation for Si, i.e., rewriting Si= f†iσσσσ′fiσ′along with the constraint ∑σf†iσfiσ= 1,where f†iσis the spinon operator. The constraint is enforced by introducing the Lagrange multiplier term ∑iλi(∑σf†iσfiσ-1)in the Hamiltonian. To study both the non-magnetic and magnetic phases, We decouple the Heisenberg Hamiltonian into two channels

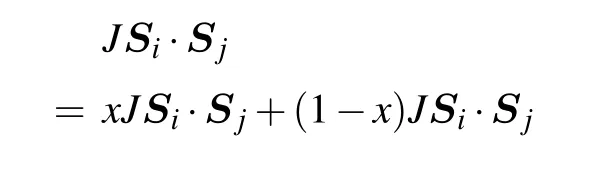
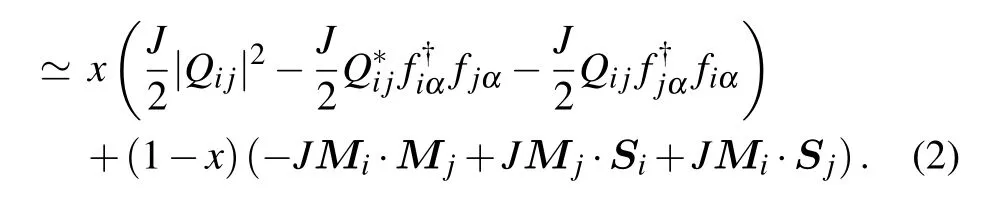
Here x is a parameter that is introduced in keeping with the generalized procedure of Hubbard-Stratonovich decouplings and will be fixed to conveniently describe the effect of quantum fluctuations. The corresponding valence bond(VB)parameter Qijand sublattice magnetization Miare Qij=〈∑αf†iαfjα〉 and Mi= 〈Si〉, respectively. Throughout this paper, we consider the two-site unit cell, thus excluding any states that break the lattice translation symmetry. Under this construction, there are three independent VB mean fields Qi,i = 1,2,3 for the NN bonds and six independent VB mean fields Qi, i=4,5,...,9 for the NNN bonds, which are illustrated in Fig.1.We consider only AFM exchange interactions,J1＞0 and J2＞0, and will thus only take into account AFM order with M =Mi∈A=-Mi∈B.

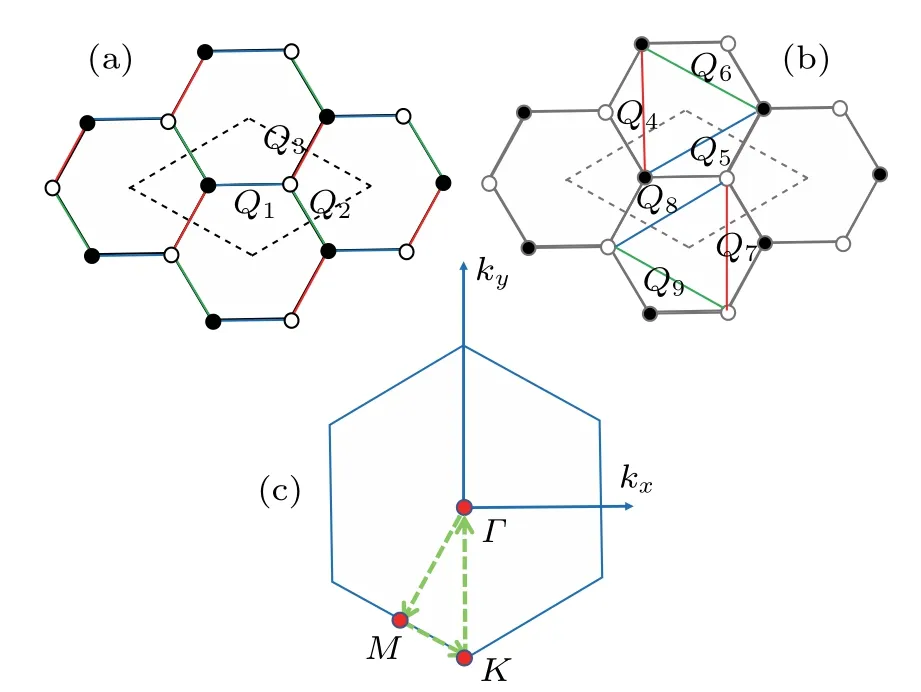
Fig.1.(a),(b)Definition of nearest neighboring and next nearest neighboring valence bond mean fields Qij. Filled and empty circles denote the two sublattices A and B,respectively. Different bond directions are labeled by different colors. (c) First Brilluion zone corresponds to the two-sublattice unit cell.

To take into account the Kondo hybridization and the possible magnetic order on an equal footing,we follow the treatment of the Heisenberg interaction as outlined in Eq. (2) and decouple the Kondo interaction as follows:

Here we have introduced the mean-field parameter for the Kondo hybridization,, and the conduction electron magnetization mi=〈si〉. For nonzero b,the conduction electrons will Kondo hybridize with the local moments and the system at half-filling is a KI.On the other hand,when b is zero and M is nonzero, magnetization (m/=0) on the conduction electron band will be induced by the Kondo coupling,and various AFM orders can be stabilized depending on the strength of the SOC.Just like the parameter x in Eq.(2)is chosen so that a saddle-point treatment captures the quantum fluctuations in the form of spin-singlet bond parameters,[19]the parameter y will be specified according to the criterion that the treatment at the same level describes the quantum fluctuations in the form of Kondo-insulator state.

3. Phase diagram of the Heisenberg model for the local moments

Because of the complexity of the full Hamiltonian, we start by setting JK=0 and discuss the possible ground-state phases of the J1-J2Heisenberg model for the local moments.By treating the problem at the saddle-point level in Eq.(2),we obtain the phase diagram in the x-J2/J1plane shown in Fig.2.Here,the x-dependence is studied in the same spirit as that for the Shastry-Sutherland lattice in Ref. [19]. In the parameter regime explored, an AFM ordered phase (labeled as “AFM”in the figure)and a valence bond solid(VBS)phase are stabilized. The AF order stabilized is the two-sublattice N´eel order on the honeycomb lattice, and the VBS order refers to covering of dimer singlets with |Qi|=Q/=0 for one out of the three NN bonds(e.g.,Q1/=0,Q2=Q3=0)and|Qi|=0 for all the NNN bonds. This VBS state spontaneously breaks the C3rotational symmetry of the lattice. We thus define the order parameter for the VBS state to be Q=|∑j=1,2,3Qjei(2πj/3)|.

In Fig. 3, we plot the evolution of VBS and AF order parameters Q and M as a function of J2/J1. A direct firstorder transition(signaled by the mid-point of the jump of the order parameters) between these two phases is observed for x 0.6. For the sake of understanding the global phase diagram of the full Kondo-Heisenberg model, we limit our discussion to J2/J1＜1, where only the NN VBS is relevant. A different decoupling scheme approach has been used to study this model,[37]and the obtained results are consistent with ours in the parameter regime of overlap. To fix the parameter x,we compare our results with those about the J1-J2model derived from previous numerical studies. DMRG studies[38]found that the AFM state is stabilized for J2/J1＜0.22, and VBS exists for J2/J1＞0.35, while in between the nature of the ground states is still under debate. In this parameter regime,the DMRG calculations suggest a plaquette resonating valence bond(RVB)state,[38]while other methods implicate possibly spin liquids.[39]In light of these numerical results, we take x=0.4 in our calculations. This leads to a direct transition from AFM to VBS at J2/J1≃0.27,close to the values of phase boundaries of these two phases determined by other numerical methods.

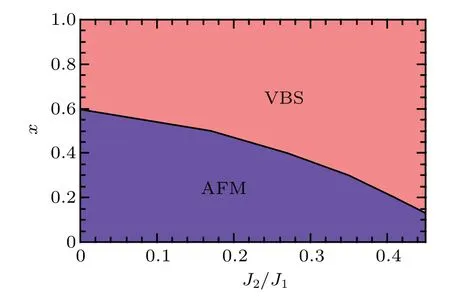
Fig. 2. Ground-state phase diagram of the J1-J2 Hamiltonian for the local moments in the x-J2/J1 plane. A NN VBS and an AFM state are stabilized in the parameter regime shown.

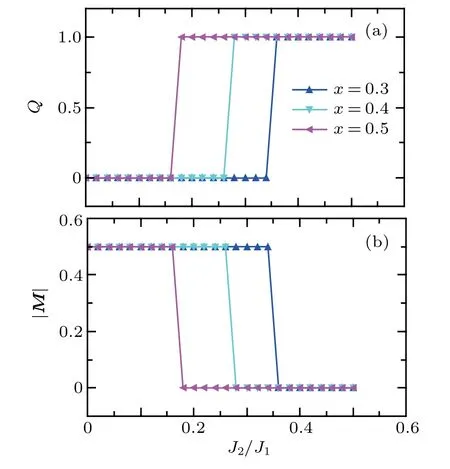
Fig. 3. Evolution of (a) the VBS order parameter Q and (b) the AFM order parameter M as a function of J2/J1 for x=0.3,0.4,0.5.

4. Global phase diagram of the Kondo-lattice model

We now turn to the global phase diagram of the full model by turning on the Kondo coupling. For definiteness, we set J1=1 and consider t =1 and λso=0.4. As prescribed in the previous section, we take x=0.4. Similar considerations for y require that its value allows for quantum fluctuations in the form of Kondo-singlet formation. This has guided us to take y=0.7 (see below). The corresponding phase diagram as a function of JKand the frustration parameter J2/J1is shown in Fig.4.

In our calculation, the phase boundaries are determined by sweeping JKwhile along multiple horizontal cuts for several fixed J2/J1values, as shown in Fig. 5. For small JKand large J2/J1, the local moments and the conduction electrons are still effectively decoupled. The conduction electrons form a TI for finite SOC, and the local moments are in the VBS ground state as discussed in the previous section. When both JKand J2/J1are small, the ground state is AFM. Due to the Kondo coupling, finite magnetization m is induced for the conduction electrons. This opens an SDW gap in the conduction band, and therefore the ground state of the system is an AFM insulator. The SOC couples the rotational symmetry in the spin space to the one in the real space. As a consequence, the ordered moments in the AFM phase can be either along the z direction (AFMz)or in the x-y plane (AFMxy). For finite SOC, these two AFM states with different energies, which can be tuned by JK. As shown in the phase diagram, the AFM phase contains two ordered states, the AFMzand AFMxy. They are separated by a spin reorientation transition at JK/J1≈0.8.For the value of SOC taken, the AFM state is topologically nontrivial, and is hence denoted as T-AFMzstate. The nature of this state and the associated topological phase transition is discussed in detail in the next section.

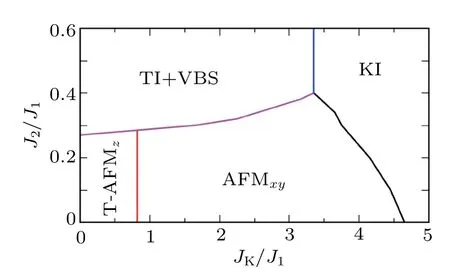
Fig. 4. Global phase diagram at T =0 from the saddle-point calculations with x=0.4 and y=0.7. The ground states include the valencebond solid (VBS) and Kondo insulator (KI), as well as two antiferromagnetic orders,T-AFMz and AFMxy,as described in Section 5.

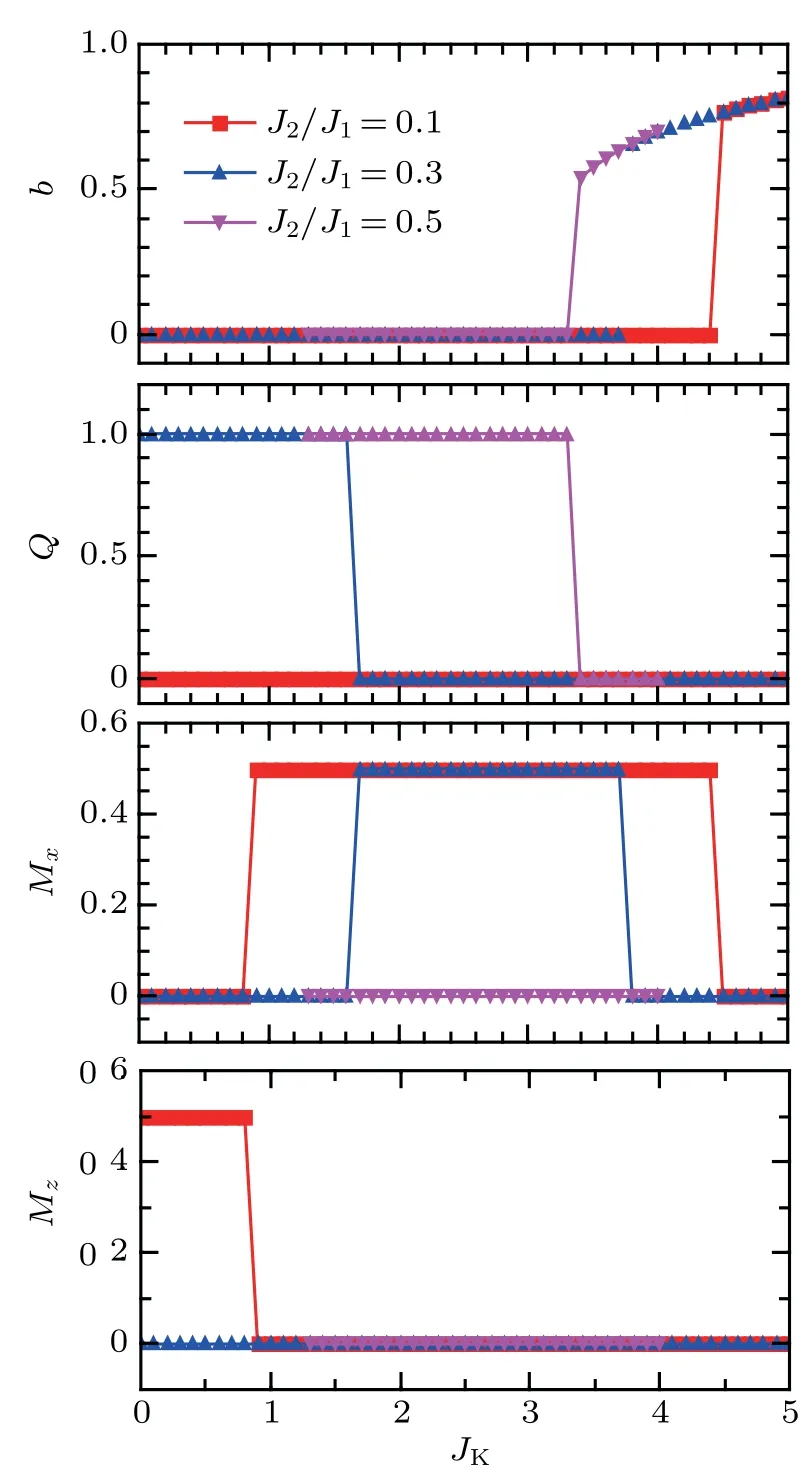
Fig. 5. Evolution of parameters (a) b, (b) Q, (c) Mx, and (d) Mz as a function of JK for different ratios of J2/J1.

For sufficiently large JK, the Kondo hybridization b is nonzero (see Fig. 5(a)), and the ground state is a KI. Note that for finite SOC, this KI does not have a topological nontrivial edge state, as a consequence of the topological no-go theorem.[30,40,41]In our calculation at the saddle-point level,the KI exists for y ≥0.6; this provides the basis for taking y=0.7,as noted earlier. Going beyond the saddle-point level,the dynamical effects of the Kondo coupling will appear,and we will expect the KI phase to arise for other choices of y.

Several remarks are in order. The phase diagram,Fig.4,has a similar profile of the global phase diagram for the Kondo insulating systems.[26,42]However, the presence of SOC has enriched the phase diagram. In the AF state,the ordered moment may lie either within the plane or be perpendicular to it. These two states have very different topological properties.We now turn to a detailed discussion of this last point.

5. Topological properties of the AFM states

In this section, we discuss the properties of the AFMxyand AFMzstates,in particular to address their topological nature. For a clear discussion, we fix t =1, J1=1, and J2=0.Since the Kondo hybridization is not essential to the nature of the AFM states, in this section we simply the discussion by setting y=0.

We start by defining the order parameters of the two states

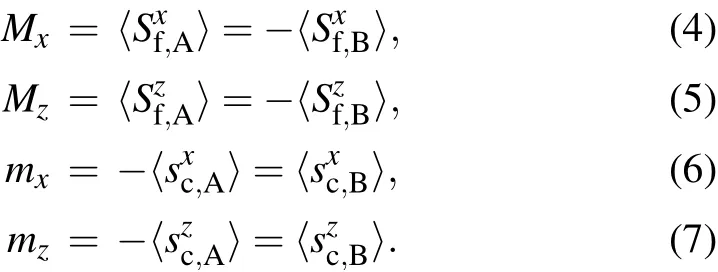
Note that for the AFMxystate,we set My=my=0 without losing generality. In Fig.6, we plot the evolution of these AFM order parameters with JKfor a representative value of SOC λso=0.1. Due to the large J1value we take, the sublattice magnetizations of the local moments are already saturated to 0.5. Therefore, at the saddle-point level, they serve as effective (staggered) magnetic fields to the conduction electrons.The Kondo coupling then induces finite sublattice magnetizations for the conduction electrons, and they increase linearly with JKfor small JKvalues. But mxis generically different from mz,which is important for the stabilization of the states.

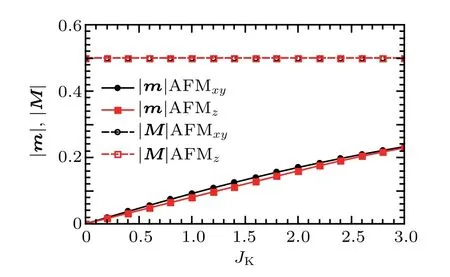
Fig. 6. The conduction electron magnetization for the AFMxy and AFMz states at λso=0.1.

We then discuss the energy competition between the AFMxyand AFMzstates. The conduction electron part of the mean-field Hamiltonian reads

with

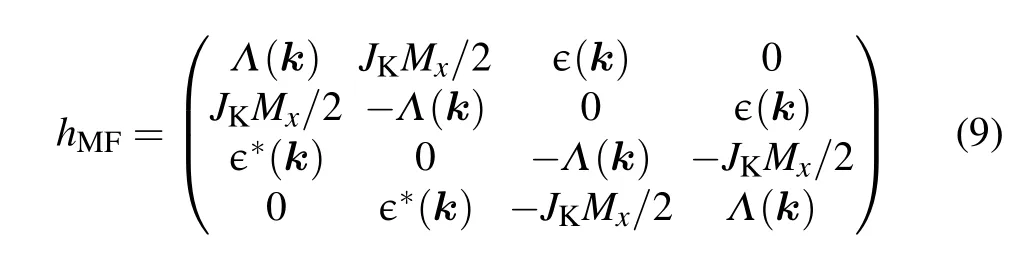
for the AFMxystate and

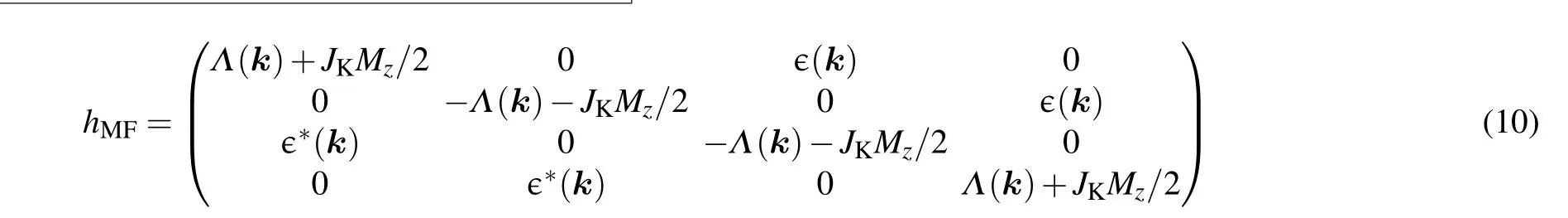
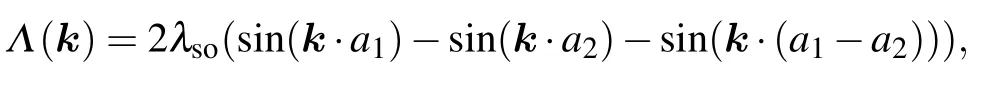
for the AFMzstate. Here=t1(1+e-ik·a1+e-ik·a2),∈∗(k)is the complex conjugate of ∈(k), and a1=are the primitive vectors. For both states,the eigenvalues are doubly degenerate

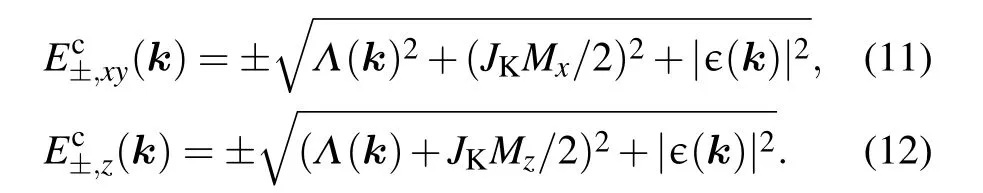
The eigenenergies of the spinon band can be obtained in a similar way

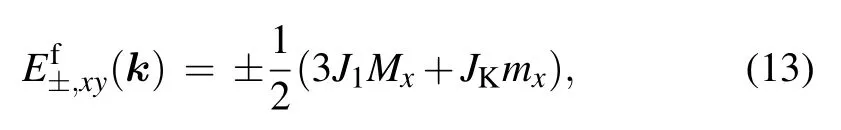
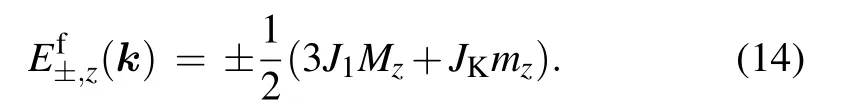
The expression of the total energy for either state is then

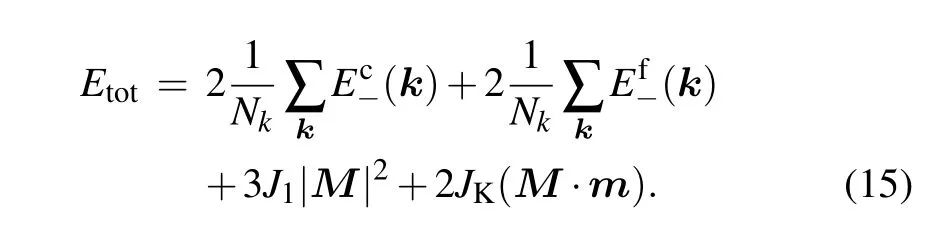
The first line of the above expression comes from filling the bands up to the Fermi energy(which is fixed to be zero here).The second line is the constant term in the mean-field decomposition. The factor 2 in the k summation is to take into account the double degeneracy of the energies. Nkrefers to the number of k points in the first Brillouin zone.

By comparing the expressions of Ec-(k)in Eqs.(11)and(12),we find that adding a small Mxis to increase the size of the gap at both of the two(inequivalent)Dirac points,thereby pushing the states further away from the Fermi-energy. While adding a small Mzis to enlarge the gap at one Dirac point but reduce the gap size at the other one.Therefore,an AFMxystate is more favorable than the AFMzstate in lowering the energy of the conduction electrons ∑kEc-(k).

Meanwhile, from Eqs.(13)-(15), we see that the overall effect of adding a magnetization of the conduction band, m,is to increase the total energy Etot(the main energy increase comes from the 2JK(M·m)term). Because|mz|＜|mx|from the self consistent solution,as shown in Fig.6,the energy increase of the AFMzstate is smaller than that in the AFMxystate.

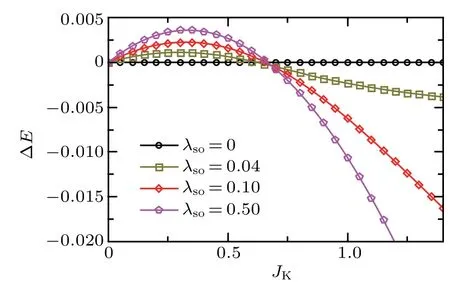
Fig.7. Energy difference between AFMz and AFMxy states as a function of JK for various values of spin-orbital coupling λso.

With increasing JK,the two effects from the magnetic orders compete,resulting in different magnetic ground states as shown in Fig.4. This analysis is further supported by our selfconsistent mean-field calculation. In Fig. 7, we plot the energy difference between these two states ΔE =Exy-Ezas a function of JKat several λsovalues. In the absence of SOC,the model has the spin SU(2) symmetry, and the AFMzand AFMxystates are degenerate with ΔE =0. For finite λso, at small JKvalues,the energy gain from the ∑kEc-(k)term dominates, ΔE ＞0, and the ground state is an AFMzstate. With increasing JK, the contribution from the 2JK(M ·m) term is more important. ΔE crosses zero to be negative, and the AFMxystate is eventually energetically favorable for large JK.

Next we discuss the topological nature of the AFMzand AFMxystates. In the absence of Kondo coupling JK,the conduction electrons form a TI, which is protected by the TRS.There, the left- and right-moving edge states connecting the conduction and valence bands are respectively coupled to up and down spin flavors (eigenstates of the Szoperator) as the consequence of SOC,and these two spin polarized edge states do not mix.

Once the TRS is broken by the AFM order, generically,topologically nontrivial edge states are no longer guaranteed.However,in the AFMzstate,the structure of the Hamiltonian for the conduction electrons is the same as that in a TI. This is clearly shown in Eq. (10) the effect of magnetic order is only to shift Λ(k)to Λ(k)+JKMz/2. In particular,the spinup and spin-down sectors still do not mix with each other.Therefore, the two spin polarized edge states are still well defined as in the TI, and the system is topologically nontrivial,though without the protection of TRS.Note that the above analysis is based on assuming JKMz≪Λ(k),where the bulk gap between the conduction and valence bands is finite. Forthe bulk gap closes at one of the inequivalent Dirac points and the system is driven to a topologically trivial phase via a topological phase transition.[30]We also note that a similar AFMzstate arises in a Kondo lattice model without SOC but with a Haldane coupling,as analyzed in Ref.[34].

For the AFMxystate,we can examine the Hamiltonian for the conduction electrons in a similar way.As shown in Eq.(9),the transverse magnetic order Mxmixes the spin-up and spindown sectors. As a result, a finite hybridization gap opens between the two edge states,making the system topologically trivial.

To support this analysis, we perform calculations of the energy spectra of the conduction electrons in the AFMzand AFMxystates, as shown in Eqs. (9) and (10), on a finite slab of size Lx×Ly, with Lx=200 and Ly=40. The boundary condition is chosen to be periodic along the x direction and open and zig-zag-type along the y direction. In Fig. 8, we show the energy spectra with three different sets of parameters:(a) λso=0.01, JK=0.4, Mz=0.5, (b) λso=0.1, JK=0.4,Mz=0.5, and (c) λso=0.1, JK=0.8, Mx=0.5, which respectively correspond to the topologically trivial AFMzstate,topological AFMzinsulator,and AFMxystate.As clearly seen,the gapless edge states only exist for parameter set(b),where the system is in the topological AFMzstate. Note that in this state,the spectrum is asymmetric with respect to the Brilluion zone boundary (kx= π), reflecting the explicit breaking of TRS. Based on our analysis and numerical calculations, we construct a phase diagram(as shown in Fig.9)to illustrate the competition of these AFM states.As expected,the AFMzstate is stabilized for,and is topological for JK＜123λso(above the red line).

Fig.8. Energy spectra of(a)the trivial AFMz state,(b)the topological AFMz insulator, and (c) the AFMxy state from finite slab calculations.Black lines denote the bulk states and red lines denote the edge states.The topological AFMz state is characterized by the gapless edge states.See text for detailed information on the parameters.

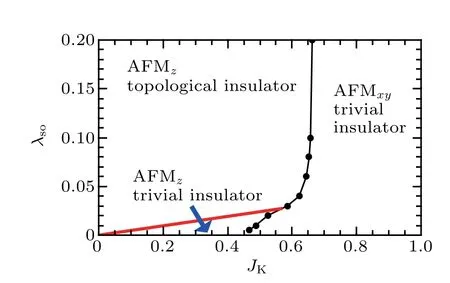
Fig.9. Phase diagram in the λso-JK plane showing the competition of various AFM states. The red line denotes a topological phase transition between the topological trivial and topological nontrivial AFMz states,and the black curve gives the boundary between the AFMz and AFMxy states. These two states become equivalent in the limit of λso →0.

6. Discussion

We have discussed the properties of various phases in the ground-state phase diagram of the spin-orbit-coupled Kondo lattice model on the honeycomb lattice at half filling. We have shown how the competition of SOC,Kondo interaction,and magnetic frustration stabilizes these phases. For example,in the AFM phase the moments can order either along the z-direction or within the x-y plane. In our model, the AFM order is driven by the RKKY interaction,and the competition of SOC and Kondo interaction dictates the direction of the ordered magnetic moments.

Throughout this work, we have discussed the phase diagram of the model at half filling. The phase diagram away from half-filling is also an interesting problem. We expect that the competition between the AFMzand AFMxystates persist at generic fillings, but the topological feature will not. Another interesting filling would be the dilute-carrier limit,where a DKSM exists, and can be tuned to a TKI by increasing the SOC.[32]

In this work, we have considered a particular type of SOC, which is inherent in the band structure of the itinerant electrons. In real materials,there are also SOC terms that involve the magnetic ions. Such couplings will lead to models beyond the current work, and may further enrich the global phase diagram.

Although the model in this work is defined on the honeycomb lattice, our conclusion on the global phase diagram is quite general, and will be important in understanding the nature of the transition between the Kondo insulating phase and the antiferromagnetic phase in real materials. For example, the Kondo insulator compound SmB6undergoes a magnetic transition under pressure.[44]The Kondo-insulatorto-antiferromagnet transition may also be realized by doping CeNiSn with Pt or Pd ions since both CePtSn and CePdSn are antiferromagnetic at low temperatures.[44-46]Nontrivial topological properties in the antiferromagnetic phase are expected given that the 5d electrons of CePtSn may contain a large SOC.Moreover, because the Kane-Mele model describes the electron states in graphene,our model may also shed light on the properties of graphene with 5d adatoms.[47]

7. Conclusion

We have investigated the ground state phase diagram of a spin-orbit coupled Kondo lattice model at half-filling. The combination of SOC,Kondo and RKKY interactions produces various quantum phases,including a Kondo insulator,a topological insulator with VBS spin correlations, and two AFM phases. Depending on the strength of SOC,the magnetic moments in the AFM phase can be either ordered perpendicular to or in the x-y plane. We further show that the z-AFM state is topologically nontrivial for strong and moderate SOC, and can be tuned to a topologically trivial one via a topological phase transition by varying either the SOC or the Kondo coupling. Our results shed new light on the global phase diagram of heavy fermion materials.