巧用“动圆”方法解带电粒子在匀强磁场中的运动问题

河北

带电粒子在匀强磁场中运动是高中物理知识中的重难点，也是历年高考必考的内容之一，在高考中经常以压轴题形式进行考查。此类题目难点是与平面几何知识结合，确定粒子各种运动情况对应的临界条件，尤其是多个粒子从不同位置以相同的速度、从同一位置以相同速率、不同方向或从同一位置以不同速率进入匀强磁场，在洛伦兹力作用下做匀速圆周运动，更需要结合几何知识确定临界条件，这是解决此类问题的关键所在，也是难点所在。对于这类题型，由于涉及多个粒子的运动，即涉及多个运动轨迹，在实际解题中，我们不可能把每个粒子的轨迹都画出来，在这种情况下，我们可以根据粒子进入磁场的速度情况，先确定某一特殊速度粒子的轨迹圆，然后让这个轨迹圆根据题意动起来，从而得到其他粒子进入磁场的轨迹，在动圆过程中结合几何知识确定符合题意的临界条件，从而找到解决问题的突破口。

一、旋转圆

大量带电粒子在垂直磁场方向的平面内从同一点O沿平面不同方向以相同大小的速度进入匀强磁场，由于大量带电粒子进入，每个带电粒子均做匀速圆周运动(只考虑带电粒子受到磁场的洛伦兹力)，每个粒子都有一个相应的运动轨迹，很显然我们无法把每个粒子的运动轨迹都画出来，由于粒子均从同一点进入匀强磁场做匀速圆周运动(该点是轨迹上的同一点)，所以这些粒子运动的轨迹均是半径相同的相交圆，根据这个特点，我们可以先确定一个方向特殊的带电粒子的运动轨迹，其他粒子的运动轨迹可以由这个轨迹绕O点做匀速圆周运动得到，在旋转圆的过程中寻找、确定题意所需要的临界条件，从而得到粒子运动过程所满足的规律。

( )

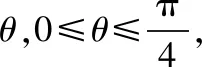
【反思】由于所有电荷均从同一平面、同一点、以大小相等、方向不同的速度垂直进入匀强磁场，电荷的轨迹均交于该点，先利用一个特殊的速度方向得到电荷运动的轨迹，其他速度方向的电荷轨迹均可由该轨迹绕该点旋转得到，在旋转圆的过程中，可以确定题意所要求的临界条件，从而使问题顺利求解。

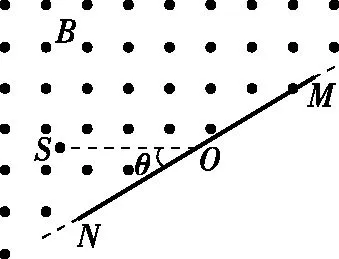
【例2】如图所示，S处有一电子源，可向纸面内任意方向发射电子，平板MN垂直于纸面，在纸面内的长度L=9.1 cm，中点O与S间的距离d=4.55 cm，MN与SO直线的夹角为θ，板所在平面有电子源的一侧区域存在方向垂直于纸面向外的匀强磁场，磁感应强度B=2.0×10-4T，电子质量m=9.1×10-31kg，电荷量e=-1.6×10-19C，不计电子重力。电子源发射速度v=1.6×106m/s的一个电子，该电子打在板上可能位置区域的长度为l，则

( )

A.θ=90°时，l=9.1 cm

B.θ=60°时，l=9.1 cm

C.θ=45°时，l=4.55 cm

D.θ=30°时，l=4.55 cm

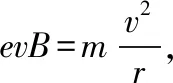
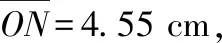
【反思】粒子进入磁场的速度大小一定，方向不定，即不同速度方向粒子的轨迹是半径相等且有公共交点的不同轨迹圆。我们以某一特殊方向的粒子轨迹为基准，其他粒子运动轨迹均可由该轨迹圆绕该点旋转得到，在旋转圆的过程中，充分利用几何关系，尤其是圆与直线的几何关系寻找临界条件，从而确定电子打在板上可能位置的区域长度。

二、平移圆

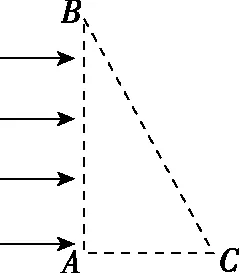
大量带电粒子在垂直磁场方向的平面，从同一直线边界上不同的点以相同速度进入匀强磁场，各电荷在匀强磁场中的轨迹为半径相同的圆弧，选一个特殊位置电荷的轨迹圆弧，平移该轨迹圆弧可以得到其余电荷在磁场中运动的轨迹圆弧，在平移过程中，结合几何关系很容易找到满足题意的临界条件，从而找到问题的突破口，使问题顺利求解。

( )

A.粒子在磁场中做匀速圆周运动的周期为4t0

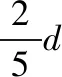
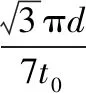
【反思】沿边界AB移动轨迹的过程中，发现轨迹在磁场中的长度先逐渐增大再逐渐减小，结合几何关系很容易判断出当电荷轨迹与BC边相切时在磁场中的轨迹最长，对应的在磁场中运动的时间最长，而这一结果恰好是本题的难点，找到了这一临界条件，就能使问题顺利求解。

【例4】一边长为a的正三角形ADC区域中有垂直该三角形平面向里的匀强磁场，在DC边的正下方有一系列质量为m、电荷量为q的带正电粒子，以垂直于DC边的方向射入正三角形区域。已知所有粒子的速度均相同，经过一段时间后，所有的粒子都能离开磁场，其中垂直AD边离开磁场的粒子在磁场中运动的时间为t0。假设粒子的重力和粒子之间的相互作用力可忽略。

采用木棉花80克、金樱花60克、麦冬60克、陈皮30克，混合均匀，采用中药粉碎机粉碎后过80目标准筛，每日1次，家禽每次2～4克，家畜每次5～6克，连续使用3～5日，用于治疗畜禽咽喉肿痛、咳嗽、失音、久咳不止、痈疽疮疖、呼吸道感染、高热死只等症状，有效率高达98.89%。也可采用木棉花木棉花80克、茵陈40克、黄连30克、甘草15克，粉碎过60目标准筛，混匀，每只鸡喂1克，拌料，用于畜禽咽喉肿痛、口腔溃烂、痈疖肿毒、不食无力、目呆，有效率高达97.34%。

(1)为了能有粒子从DC边离开磁场，则粒子射入磁场的最大速度为多大？

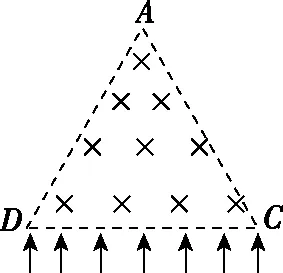
(2)若粒子以(1)中的最大速度进入磁场，则粒子从正三角形边界AC、AD边射出的区域长度为多大？

【解析】(1)洛伦兹力提供向心力，根据牛顿第二定律有

当粒子垂直AD边射出时，D点为粒子做圆周运动的圆心，粒子轨迹对应的圆心角为60°，则

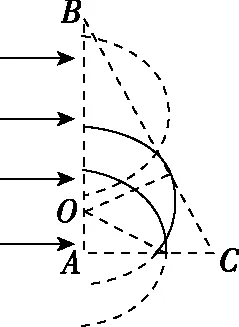
根据几何关系可知，当轨迹圆与AC、AD两边同时相切时有粒子从DC边射出，且速度为最大值的临界条件，如图所示，设此时粒子的速度为v1，偏转半径为r1，则

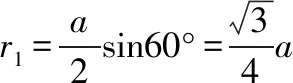
根据牛顿第二定律有

(2)把第(1)问中的轨迹圆向右平移，即可得到从DC边上该点右侧射入磁场粒子的轨迹，在平移过程中轨迹与AC边相交，表示粒子从AC边上射出，由于粒子逆时针运动，轨迹与AC边的第一个交点即为射出磁场的点，该交点逐渐从E点移动到C点，即粒子从AC边射出的范围为CE段。

再把第(1)问中的轨迹圆向左平移，即可得到从DC边上该点左侧射入磁场粒子的轨迹，在平移过程中轨迹与AD边相交，表示粒子从AD边上射出，且交点先逐渐向上移动，到达最高点F后再逐渐向下移动到D点，DF即为粒子从AD边射出的范围，由几何关系知，向左平移圆过程中与AD边的交点F恰在圆心O正上方时，射出的粒子距D点最远，如图所示，根据几何关系有

【反思】在本题中，把第(1)问中的轨迹圆分别向左、右平移即可得到其他位置射入磁场的粒子轨迹，在平移圆的过程中结合几何关系很容易得到粒子分别在AC边和AD边射出的范围，从而使问题顺利求解。

三、缩放圆

当带电粒子以任一速率从同一位置沿特定方向射入匀强磁场时，由于速率的不确定，造成带电粒子的半径不同，但所有粒子的轨迹均过同一点(进入磁场时的入射点)且圆心均在入射点初速度方向的垂线上，这时我们可利用缩放圆来进行临界条件的判断：以入射点为定点，圆心位于入射速度的垂线上，将圆的半径缩小或放大(一般让半径逐渐增大)，从而探索出临界条件，问题便迎刃而解。

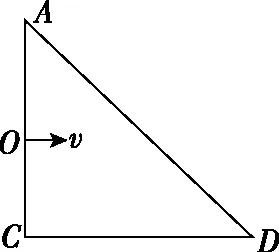
【例5】如图所示，在一等腰直角三角形ACD区域内有垂直纸面向外的匀强磁场(图中未画出)，磁场的磁感应强度大小为B，一质量为m，电荷量为q不计重力的带正电粒子从AC边的中点O垂直AC边射入该匀强磁场区域，已知三角形的直角边长度为2L，下列说法正确的是

( )

C.当粒子从AD边离开磁场时，粒子入射速度越大，在磁场中运动的时间越短

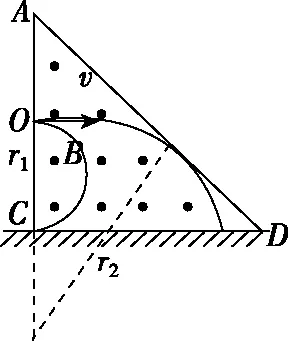
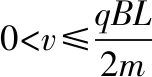
【反思】当粒子的入射速度逐渐增大时，对应的轨道半径也随之增大，但不同速度的粒子在磁场中对应的部分轨迹圆均过同一点，且圆心均在同一直线上发生变化，随着轨道半径逐渐增大，结合几何关系很容易判断出粒子离开磁场时轨迹与磁场边界对应的临界条件，从而找到解决问题的突破口。

【例6】如图所示边长为L的正方形abcd内有垂直于纸面向里、磁感应强度为B的匀强磁场，一束速率不同的带正电粒子从左边界ad中点P垂直射入磁场，速度方向与ad边夹角θ=30°，已知粒子质量为m、电荷量为q，粒子间的相互作用和粒子重力不计，则

( )

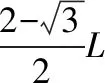
【解析】同一粒子在同一匀强磁场运动时间与粒子在磁场中做圆周运动轨迹对应的圆心角成正比，结合几何关系可知，当粒子以较小速度进入磁场且从Pa边离开磁场时轨迹对应的圆心角最大，粒子在磁场中运动的时间最长，对应的轨迹如图所示。

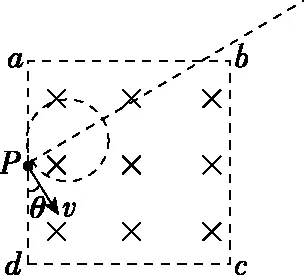
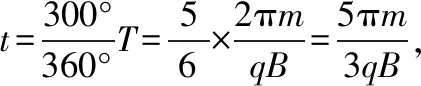
逐渐增大粒子速度，则粒子将分别从ab边、bc边和dc边射出磁场，轨迹对应的圆心角逐渐减小，当速度很大时，粒子近似可认为沿着直线穿过磁场，时间无穷小，即粒子在磁场中运动的最短时间趋向零，选项B错误。