具有马尔科夫特性的云存储改进优化算法*

王 辉，洪 波，唐俊勇

(西安工业大学 计算机科学与工程学院，西安 710021)

伴随物联网技术的迅猛发展，智能移动终端为人们提供了更为便捷的信息交互、购物以及娱乐的方式。然而传统的云存储系统有很多问题，比如存储密度低，存储效率不高，导致传统云存储方式不能广泛应用在各种不同的环境中[1-3]。其不能保证云数据的完整性和机密性，云存储服务商既不能向移动用户确保其数据和操作不被恶意或非恶意地丢失、破坏、泄漏或非法利用，也不可能消除潜在的内部攻击，若将数据直接存储在云上，会导致非常严重的后果[4]，安全优化方案的重要性取决于该存储方案失效后对系统可靠性的影响程度。现有的研究多采用简单的加密技术[5]，但存在密钥管理等问题，并且在查询、并行修改、细粒度授权等复杂情况下束手无策[6-7]。

考虑到数据量很大时，基于属性加密技术(Attribute-Based Encryption,ABE)的效率较低,云存储中海量敏感数据的机密性以对称密码体制实现,ABE仅用于保护数据量较小的对称密钥[8-10]。文献[11]提出了一种动态多副本可证明数据拥有方案。文献[12]提出一种基于云存储的密文全文检索模型,给出基于可搜索加密技术的密文全文索引构建和检索策略,并对方案的安全性进行分析。文献[13] 将马尔科夫理论和服务质量结合，在定义了基于业务开销最小的服务能力匹配度的基础上构建了网络可用性评价模型。这些研究不同于以往对云数据服务的研究，仅用单一加密方式实现安全性，缺乏云数据随机性特点。因此，文中拟将马尔科夫链[14-15]的转移概率引入到安全云存储优化算法中，提出具有马尔科夫特性的云存储改进优化算法，在分析计算各节点存储代价的基础上，采用再加密技术及优化技术，构建移动端云存储系统的安全优化模型。

1 基于马尔科夫链的安全云存储优化模型

1.1 云存储有限状态空间及状态分布

基于马尔科夫链的安全云存储优化算法由3部分组成{S,R,P}。其中S为云系统的状态空间，R为状态分布，P为状态转换概率。将云存储系统中存储节点(服务器)可存储的数据按大小分为4类，分别为小密度文件、中密度文件、高密度文件及大密度文件。不超过10 MB的文件定义为小密度文件，存储文件超过1 000 MB时称之为大密度文件，介于10 MB和100 MB之间的文件被定义成中密度文件，介于100 MB和1 000 MB之间的文件被定义成高密度文件。云系统中节点的硬件性能、网络带宽及延迟等均不同，存储节点在完成大、高、中、小4种不同密度的数据访问所耗费的代价也会不同，此外，考虑云数据的安全性，采用不同的加密技术耗费的时间也不同。在云系统中，根据存储数据文件大小的不同，每个节点存储大、高、中、小4种文件耗费的存储代价也就不同，选择代价最小的节点实现存储。

根据上述分析，存储节点存储4类不同大小密度文件的存储过程可以近似成离散的状态空间S，存储节点的选取仅和节点的存储代价有关，云系统的这一存储特点符合马尔科夫链的特征。本文将云存储系统的状态空间表示为S，不同大小的密度文件分别表示不同的状态，因此，4种密度文件对应4种状态。例如，小密度文件状态表示在实现云存储时会选择存储小密度文件的最优存储节点。

基于马尔科夫链的云存储的状态空间采取如下定义：

S={s1,s2,s3,s4}

式中：s1为机群中各个存储节点实现小密度文件存储的的存储代价；s2为机群中各个存储节点实现中密度文件存储的存储代价；s3为机群中各个存储节点实现高密度文件存储的存储代价；s4为机群中各个存储节点实现大密度文件存储的存储代价。

在移动端云存储系统中，存储状态划分越细，在云存储策略中执行算法所需的开销越大，系统收敛稳定的时间也越长；反之，当存储状态划分非常简单时，可以减少系统的计算开销及收敛时间，有利于从现实系统中抽象出模型状态进行分析。因此，根据云存储的实际需要，在本文提出的云存储模型中采取折中做法，将系统存储状态定义为4种。存储方案的硬件设备的冗余性及其配置使存储策略算法分析变得更加复杂，同时也降低了移动端云存储系统的存储速率。所以，云存储优化算法中存储状态要划分适度。本文定义云存储的大密度文件、高密度文件、中密度文件、小密度文件4种状态，在云系统的数据统计或存储分析实际应用中，这4种状态均能满足云系统对数据存储的要求。

存储组机群采用不规则连接网络的方式，用R表示状态分布，指某节点实现数据存储所需耗费的存储代价，根据存储节点在大、高、中、小4种不同状态的存储代价，得到ti时刻的状态分布矩阵R(i)，将R(i)表示为

(1)

其中si为云系统在ti时刻某节点所耗费的存储代价，且si∈[0,1]，根据ti时刻节点的各项硬件指标进行归一化求得。

1.2 云存储状态转移概率矩阵

假设一个状态空间由n个状态构成，其状态之间的转移概率可以用状态转移概率矩阵P表示，状态转移概率矩阵P始终保持不变。P为n阶方阵，若t1,t2,…,tn的时间间隔均相同，根据齐次性，其表达式为

(2)

显然，转移概率矩阵有如下两个性质，表达式为

(3)

式中：pij为从状态si向状态sj转移的概率，Δt为时间间隔。状态转移概率矩阵P的每行元素的和均为1，指从第si转移到其余所有sj的概率总和为1。

由前述可得，云系统中存储节点可以存储4种不同密度的文件，对应4种不同的存储代价。选择某节点作为数据存储的判断依据是其存储不同大小文件的存储代价，若存储代价最小，则优先选择完成数据存储，否则，存储代价越大，利用该节点完成数据存储的概率越小。因此，云系统状态空间S={s1,s2,s3,s4}的状态转移如图1所示。

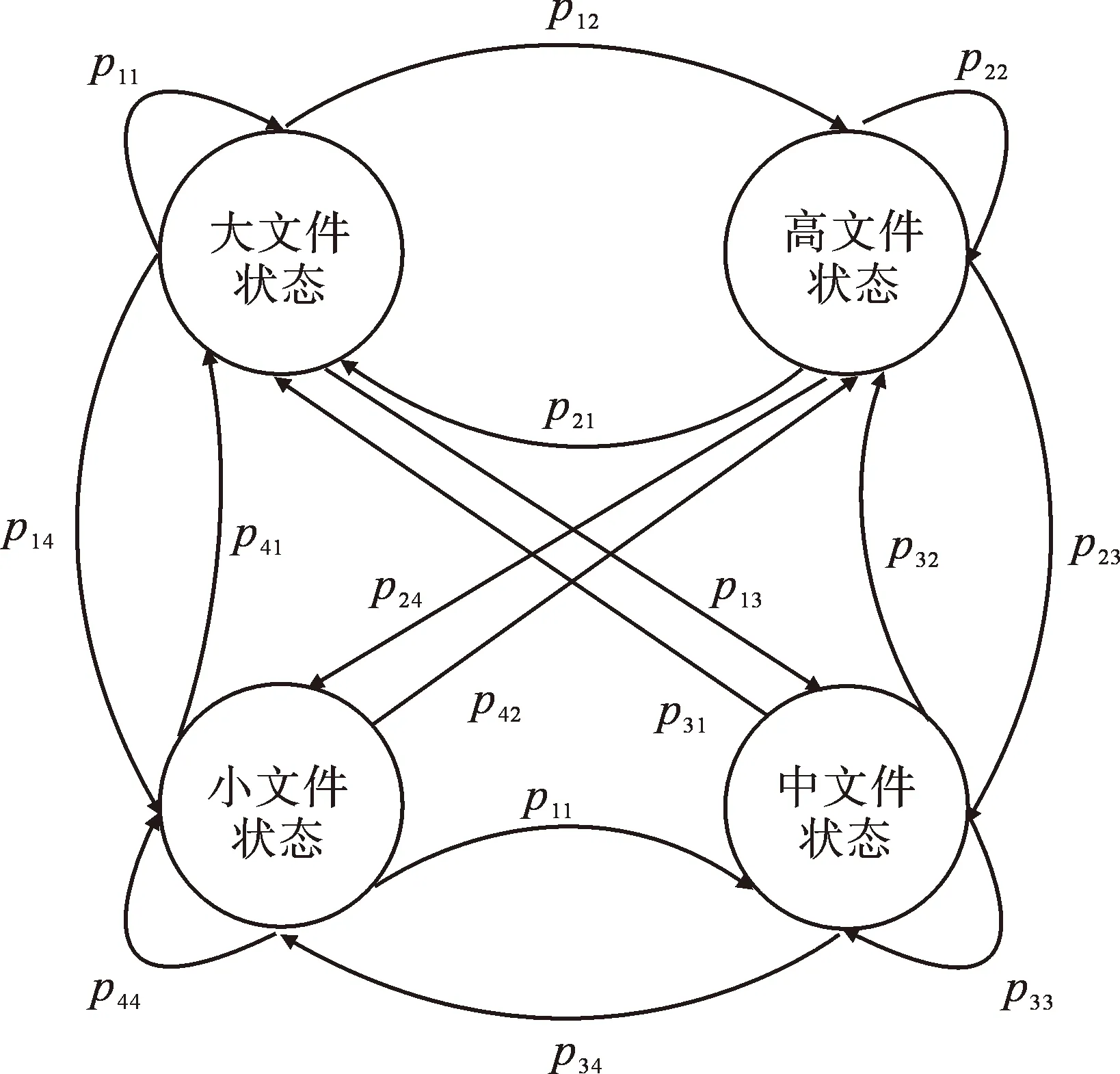
图1 存储状态转移图Fig.1 Storage status transition diagram

由存储节点在不同状态下转换的概率值，可得云系统优化模型的状态转移概率矩阵为

(4)

1.3 安全云存储算法及优化

移动终端接入网络时会选择存储组机群中存储代价最低的设备完成数据存储。为了提高移动端云存储的可靠性，在云存储系统中引入了多副本机制，且该机制能够提高移动端云存储系统的存储效率。当移动终端发出存储请求时会选择距离最近的副本，也即存储代价最低的节点。此外，传统的云存储系统仅当主副本错误时才会向备用副本发出请求，从而降低存储速度。因此，文中利用马尔科夫的相关理论，根据节点的硬件性能、网络带宽及延迟等指标计算节点所需存储代价，通过状态转移概率矩阵求得一步转移状态矩阵，进而求得多步转移矩阵来计算并预测云系统中某节点的存储概率，以此达到选择最小代价节点完成存储的目的。

云存储优化算法(Cloud Storage Optimization Algorithm,CSOA)的思路包括如下几点：首先，构建云存储系统状态划分的准则依据；其次，根据该准则对云系统划分状态并建立存储系统的状态空间；此后，由系统提供的历史数据计算得到云存储系统的马尔科夫状态转移概率矩阵；最后，利用上一步的状态转移概率矩阵及当前时刻的存储状态矩阵，计算并预测下一时刻的存储概率，实现数据存储及可靠性指标。

基于马尔科夫链的云存储策略算法步骤如下：

1)获取云存储系统初始t0时刻的存储状态分布矩阵R(0)；

2)根据t0时刻存储的状态分布矩阵，以及状态转移概率矩阵P，得到Δt时间后，下一时刻云存储系统的一步状态分布矩阵R(1)表达式为

R(1)=R(0)P

(5)

3)Δt时间后，移动端云存储系统存储状态变为

R(2)=R(1)P=R(0)P2

(6)

同理，经过m个Δt后的云系统存储状态分布为

R(m)=R(m-1)P=R(0)Pm

(7)

当R(0)及P均已知时，就能快速预测未来每隔Δt时刻后云存储系统的状态分布的稳态值。

云存储系统的状态分布矩阵在式(1)中给出，该矩阵是根据系统中不同节点实现存储所耗费的存储代价计算得到，计算过程如下。

存储代价s与长度q、延迟d和丢包率l有关，其表达式为

s=λqsq+λdsd+λlsl

(8)

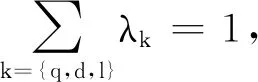
(9)

属性q由存储数据块长度表示，在初始时刻，根据数据延迟d和丢包率l，计算该节点的存储代价，综合分析各节点耗费的代价，评估其存储质量，最终更新获取各阶段的存储状态分布矩阵。

很明显，在基于Markov的云存储优化算法中，利用云系统初始时刻的状态分布矩阵R(0)及状态转移概率矩阵P，可以得到下一时刻状态分布，并通过矩阵运算实现云存储方案的选择。

存储优化问题可以表示为

(10)

制约条件为：

ρ≥ρl，ro≤rin≤r3max，0≤rout≤ro

式中：wk为存储代价Ck的权重；ρ为网络实际的丢包率；ρl为丢包率的阀值；rin为文件输入速率；ro为瓶颈带宽；r3max为链路最大带宽；rout为文件输出速率。每个节点的存储代价权重可用于相应地调整其算法性能，如性能评估部分，可以针对存储算法设计参数求解的确定性程序。通常，由于驻留分布和存储代价分布的非线性，所得到的程序在设计参数中是非线性的。因此，该问题被归类为具有边界约束的非线性优化程序，使用不同的数值技术来实现非线性程序的解决方案。采用的优化技术应当简单，易于实现，并且可以无限制地应用于任何模型。

在优化周期的开始，存储算法的参数包括带宽利用率ρb，输入速率rin和输出速率rout，可用所有涉及的随机参数(不同区域中的停留时间)来估计。显然，在优化周期的第一阶段结束时，通过改进优化算法的执行降低系统的缓存需求，并在此基础上根据展开的信息来实现预组估计。与之前的分析类似，可以根据此阶段开始时的缓冲级别来估计更新。因此，可以通过求解下式来优化存储代价，即：

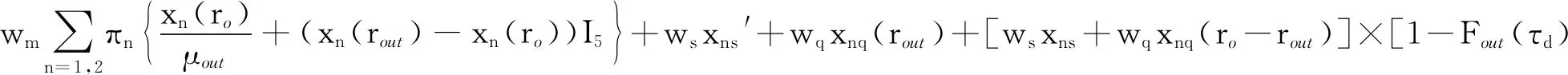
(11)

制约条件为：0≤rout≤ro

式中：μout为节点设备内存占用量；πn为速率影响因子；Fout为存储文件时节点设备的CPU占用率；τd为文件大小。

2 实验与结果分析

在前文所述思想、模型的基础上，采用python语言实现本文所提算法，并通过算例来验证云存储策略的Markov特性。

使用蒙特卡罗法连续模拟8 000次，模拟的间隔时间为300 ms，分析这些模拟获取的存储状态数据以及不同间隔后它们的改变，得到云系统的状态转移概率矩阵P为

(12)

状态转移概率矩阵P中数据元素的含义为，假设云存储系统当前在大密度文件状态，下一时刻转移到小密度文件状态、中密度文件状态和高密度文件状态概率分别为0.866，0.013和0.085，而维持大密度文件状态概率为0.016。

由于云系统中存储节点的硬件性能、网络带宽及延迟等均不同，节点完成数据访问所耗费的代价也不同。假设初始t0时刻，大、高、中和小4种存储状态的存储代价分别用s1，s2，s3和s4表示。由式(1)可得到云存储系统t0时刻的存储状态分布矩阵R(0)为

(13)

将式(12)和式(13)代入式(5)，得到一步存储状态分布矩阵R(1)，经过多步转移，可快速预测某时刻ti的存储状态分布矩阵R(i)为

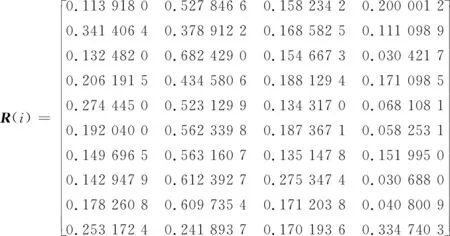
(14)

通过存储状态分布矩阵R(i)，可快速选出存储成本最低的结点进行实时存储。针对数据存储，云存储优化算法测试了不同大小密度文件在云系统数据移动和复制过程中所需的响应时间，并对算法的存储效率进行了比较。通过仿真实验验证了云系统中各存储业务均能在规定的时间内及时响应，且业务响应时间的对比数据如图2所示。

从该业务响应时间对比图中得到业务平均响应时间，尽管某个业务的响应时间较长，但其他大部分业务的响应时间较快，由此可见，本文提出的云存储优化算法的性能较好。移动端上传下载数据的测试结果见表1～2。

CPU占用率与上传速度的比率见表1，移动端数据分别在加密前和加密后进行测试。CPU占用率与下载速度的比率见表2，其中移动端数据分别在解密之前和解密之后进行测试。

从表1和表2可知，如果加密和解密机制用于移动端数据传输，那么CPU利用率将平均增加22%～25%，整体文件传输速率将降低 30%～35%。当使用加密和解密机制时，移动端可能导致性能损失3倍以上。

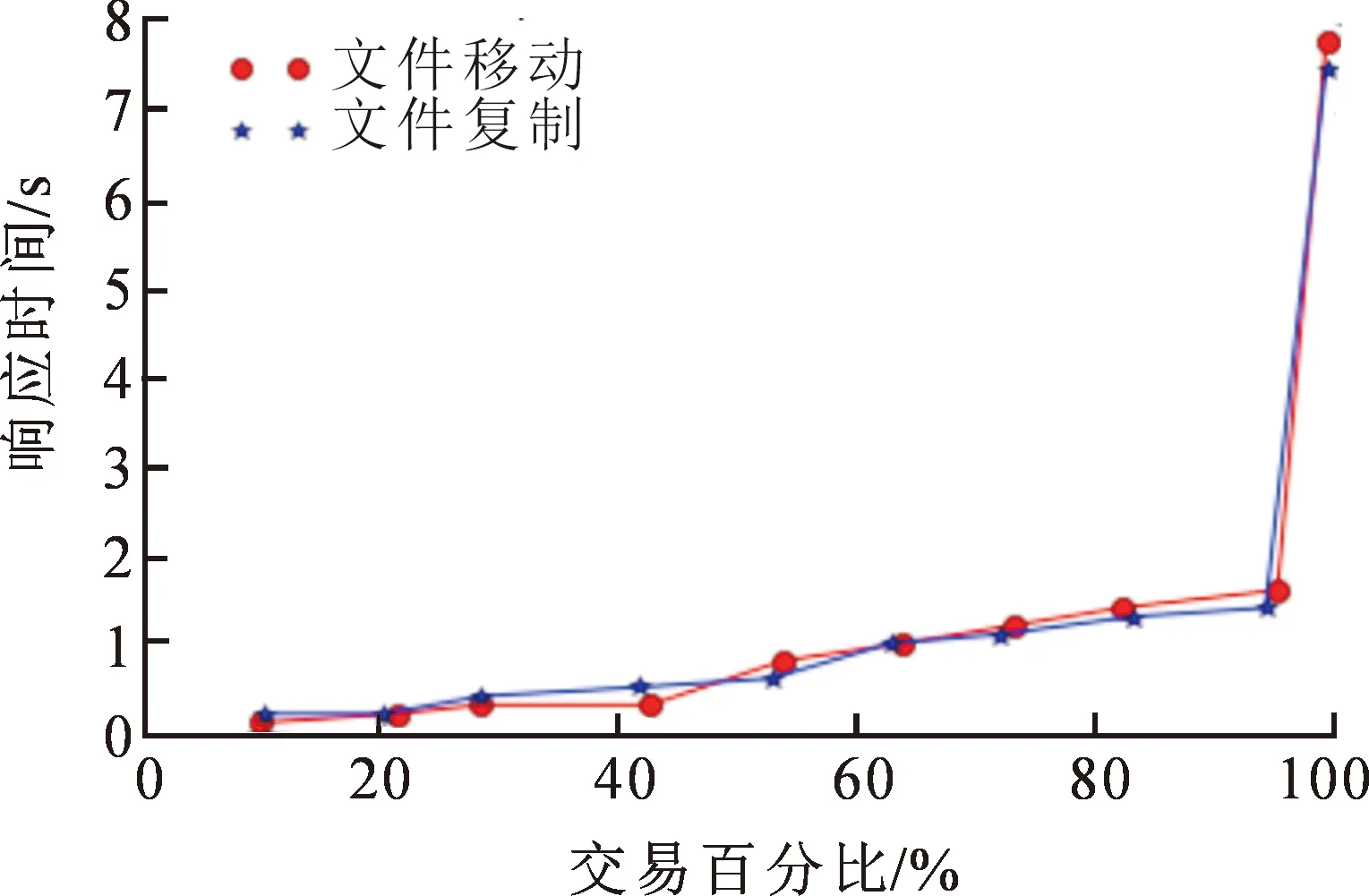
图2 业务响应时间对比图Fig.2 The comparison of the response times for the business

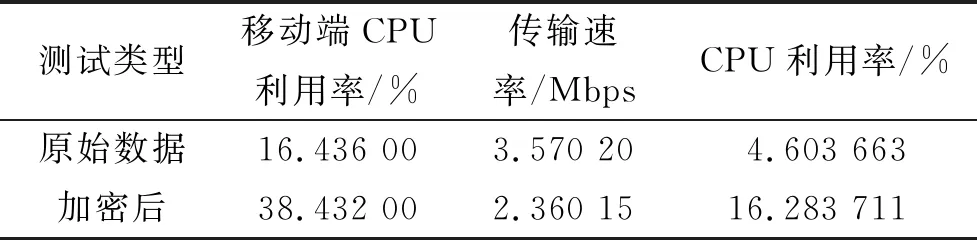
表1 移动端上传数据性能比较Tab.1 The performance of the mobile end uploading the data

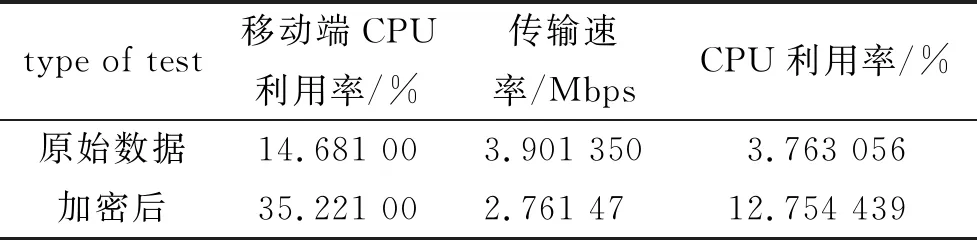
表2 移动端下载数据性能比较Tab.2 The performance of the mobile end downloading the data

考虑测试数据选取500个用户，可用节点从500到5 000不等。云服务器存储空间获得超过100个字节，并使用数据库进行存储。需考虑2个问题：① 加密和解密对文件速度的影响；② 加密和解密对客户端主机性能的影响。表3列出了加密解密时间实验数据，其中包括加密不同大小或不同类型文件所花费的时间以及在HDFS中传输文件所花费的时间。

针对论文提出的云存储算法，结合表3中对同等大小的文件，采用不同的加解密算法进行可靠性分析。在本文所述思想、模型、存储策略的基础上，仿真实验中采用不同的高级加密标准(Advanced Encrytion Standard,AES),公钥加密(Rivest Shamir Adleman,RSA)以及RSA+AES算法对本文所述的云存储策略的安全性予以验证。通过一系列的仿真实验验证了本文提出的云存储优化算法能够根据存储状态矩阵和状态转移概率矩阵实现云系统中存储状态的预测，优先选择存储代价最低的存储节点，实现数据存储。此外，云存储优化算法还可以有效节省时间，减小在文件大小不同、存储方法相同情况下存储效率降低的影响。

表3 加密解密时间对比Tab.3 Comparison of encryption and decryption times

3 结 论

本文提出将马尔科夫理论应用于云系统以解决数据存储问题，存储优化算法能够准确预测并实现数据的安全存储。将云存储的状态划分为4种状态，并获得节点的硬件指标；利用马尔科夫理论存储大、高、中、小文件，由各节点实现存储所需的存储代价得到当前存储状态矩阵，通过大量的样本数据统计得到状态转移概率矩阵，根据状态矩阵和转移矩阵预测出下一时刻云存储的状态概率，实现最优节点的选择及优化。仿真数据表明安全存储优化算法可以根据文件大小变化，预测并选择存储代价最低的节点实现存储，有效减小了在文件大小不同、存储方法相同情况下存储效率降低的影响。通过仿真实验验证了移动端云系统状态转移的马尔科夫特性，表明了基于马尔科夫链的安全云存储优化算法的高可靠性。

此外，云存储系统具有较高安全性，依据输入输出及完整性校验的特点，可以在移动端使用AES算法加密用户上传的数据，确保移动端数据的机密性；同时使用RSA算法确保AES密钥的安全性，并能解决AES单钥密码的分发和管理；通过基于Markov的云存储算法研究，设计3种存储状态从而实现移动端的数据存储，减少副本数，提高移动端云存储系统的存储效率。