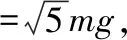运用“旋转法”求解动态平衡问题
2019-08-05甘肃
甘肃
动态平衡是高中物理力学部分的一种重要习题类型,也是高考的重要考点。动态平衡的习题教学中,学生通过正确的受力分析,做出力的矢量三角形,灵活运用三角形的边角关系、几何圆的性质等数学知识,由矢量三角形的动态变化分析物体所受力的变化情况。通过对实际情景的分析、概括,将实际情景转化为物理问题,突出主要因素、忽略次要因素,建构物理模型;运用对比、分析、概括等思维方式,经历科学推理、科学论证等思维过程,逐步提高科学思维能力。
根据物体受力的变化特征,动态平衡问题可以分为三种类型,解决问题的最典型方法是图解法。为了使学生更好地掌握图解法的具体操作要领,体验清晰的思维过程和发展思维能力,笔者将图解法延伸为更加具体的“旋转法”,并且将三种类型动态平衡问题的解题方法分别称为“单边定向旋转法”“单边定长旋转法”和“双边定角旋转法”。现将旋转法的具体思路及拓展应用例析如下。
一、旋转法的具体思路
1.单边定向旋转法
动态平衡问题中,若物体受到的三个力满足“一个力大小、方向均不变,另一个力方向不变、大小变化,第三个力大小、方向都变化”的变化特征,通过力的合成(或力的分解)构成力的矢量三角形,按三个力的具体特征将三角形的三个边分别标号1、2、3。“1”号对应大小、方向均不变的力,“2”号对应方向不变、大小变化的力,“3”号对应大小、方向都变化的力。在动态变化过程中,矢量三角形要满足1、2号两边对应力的要求,必须绕1号、3号两边的交点按照题意所给的方向旋转3号边,2、3号的交点位置变化,矢量三角形变化,可以依据2、3号边的边长变化判断对应力的大小变化,依据1、3号边之间的夹角变化判断3号边对应力的方向变化。这种情景下,旋转的只有3号边,2号边的方向一定,所以这种旋转法简称为“单边定向旋转”。
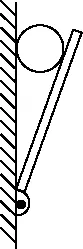
图1
【例1】如图1,一小球放置在木板与竖直墙面之间。设墙面对球的压力大小为FN1,球对木板的压力大小为FN2。以木板与墙连接点所形成的水平直线为轴,将木板从图示位置开始缓慢地转到水平位置。不计摩擦,在此过程中
( )
A.FN1始终减小,FN2始终增大
B.FN1始终减小,FN2始终减小
C.FN1先增大后减小,FN2始终减小
D.FN1先增大后减小,FN2先减小后增大
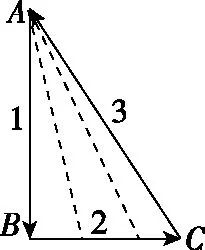
图2
【解析】对小球进行受力分析,由力的合成构成矢量三角形ABC,如图2所示。其中AB边表示小球受的重力G、BC边表示墙面对球的压力FN1、AC边表示木板对球的支持力FN2。由题意可知,重力G大小、方向均不变、压力FN1方向不变、支持力FN2大小、方向都变化。所以,将AB、BC、AC三边分别标号1、2、3,绕1、3号边的交点A顺时针旋转3号边AC,矢量三角形边长2、3逐渐变短,说明压力FN1、支持力FN2都始终减小。
2.单边定长旋转法
动态平衡问题中,若物体受到的三个力满足“一个力大小、方向均不变,另一个力大小不变、方向变化,第三个力大小、方向都变化”的变化特征,则在力的矢量三角形中,大小、方向均不变的力对应1号边,大小不变、方向变化的力对应2号边,大小、方向都变化的力对应3号边。要满足1、2号两边对应力的要求,必须以1、2号边的交点为圆心,以2号边的长度为半径按照题意方向旋转做出圆弧,使2号和3号边的交点始终在圆弧上移动,矢量三角形随之变化。根据矢量三角形的变化判断2号边对应力的方向变化情况和3号边对应力的大小、方向变化情况。这种旋转情景中,2号边的长度保持不变,这种旋转法简称为“单边定长旋转”。

图3
【例2】如图3所示,两物体通过三段轻线悬挂,不计一切摩擦,两物体静止时OB线水平,AO线与竖直方向的夹角小于45°,现把定滑轮B缓慢竖直向上移动,设线足够长,此过程中
( )
A.结点O的位置不动
B.结点O的位置先升高后降低
C.结点O的位置先降低后升高

图4
D.结点O的位置一直升高
【解析】将三段轻线的结点作为研究对象,进行受力分析,构建矢量三角形DEF,如图4所示。将矢量三角形的边DE、EF、DF分别标号1、2、3,以1、2号边的交点E为圆心,以2号边EF的长度为半径逆时针方向旋转做出圆弧,使F点 在圆弧上的位置变化,矢量三角形随之变化。动态变化过程中由几何关系看出DE和DF边的夹角先增大后减小,表示OA段轻线的拉力方向与竖直方向的夹角先增大后减小,即结点O的位置先升高后降低。同时,还可以判断OA段轻线的拉力大小逐渐减小。
3.双边定角旋转法
动态平衡问题中,若物体受到的三个力满足“一个力大小、方向均不变,另两个力间的夹角保持不变”的变化特征,则可以在力的矢量三角形中,将大小、方向均不变的力对应的边标号为1,另两个边分别标号2、3。根据几何圆中“弦长一定时,弦对应的圆周角一定”这一性质,可以将1号边作为定弦做出辅助圆(矢量三角形的外接圆)。根据题意同时旋转2、3号边,矢量三角形随之变化,依据2、3号边长度变化判断对应两个力的大小变化。这种旋转简称为“双边定角旋转”。

( )
A.MN上的张力逐渐增大
B.MN上的张力先增大后减小
C.OM上的张力逐渐增大
D.OM上的张力先增大后减小

图5

图6
【解析】对重物受力分析,做出矢量三角形GHI,如图6所示。将重力对应边标号为1,另两边分别标号2和3。由于OM与MN间的夹角α不变,所以矢量三角形GHI中GI与HI间的夹角为π-α,且保持不变。以GH边为弦,π-α角为对应的圆周角做出辅助圆,在小球被拉起的过程中,矢量三角形随之变化,可以看出2号边HI的长度一直增大,3号边GI的边长先增大后减小。所以,MN上的张力逐渐增大,OM上的张力先增大后减小。
二、旋转法的拓展应用
当物体受到四个力的作用处于动态平衡状态时,可以将某两个力等效为一个力,构成矢量三角形。根据矢量三角形中三个力的变化特征确定动态平衡的类型,巧妙应用旋转法准确、直观地分析物体所受力的变化情况。

图7
【例3】如图7所示,一质量为m的铁环套在粗糙的水平横杆上,通过细线连接一质量也为m的小球,小球还用一水平细线拉着。保持环和小球的位置不变,横杆的位置逐渐按图示方向转到竖直位置,在这个过程中环与杆相对静止,则
( )
A.连接环和小球的细线拉力增大
B.杆对环的作用力逐渐增大
C.杆对环的弹力的最小值为2mg
D.杆对环的摩擦力的最大值为2mg



甲
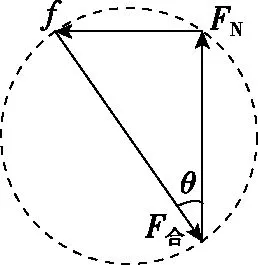
乙
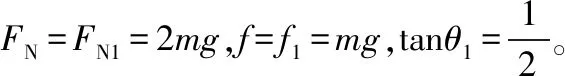
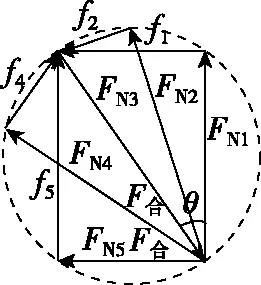
图9