类斜抛运动的多角度分析
2019-08-05安徽
安徽
人民教育出版社出版的《普通高中物理课程标准》中明确指出:高中物理课程旨在落实立德树人的根本任务,进一步提升学生的物理学科核心素养,为学生的终身发展奠定基础,而学科核心素养是指通过学科学习而逐步形成的正确观念、必备品格和关键能力。曲线运动是高中物理的重要内容,运动的合成与分解是一种等效的思想方法,是将许多实际问题通过建构物理模型,应用数学方法,化曲为直、化繁为简,把复杂的运动通过简单的运动进行分析,蕴含着丰富的科学思想和内涵,是联系直线运动与曲线运动、联系动力学与电磁学的重要桥梁和纽带。在高三教学复合场中类平抛运动和类斜抛运动是教学重点,受限制的类斜抛运动、类斜抛运动中极值问题是教学的难点,对此类问题进行多角度分析,通过剖析一题多解的实质,活化物理思想、物理规律,起到融会贯通的作用,落实学科核心素养,有效培养学生的创新思维能力和发散思维能力,达到事半功倍的效果。
一、受限制类斜抛运动的多角度分析
【例1】如图1所示,平面直角坐标系第一象限中,两个边长均为L的正方形与一个边长为L的等腰直角三角形相邻排列,三个区域的底边均在x轴上,正方形区域Ⅰ和三角形区域Ⅲ存在大小相等,方向沿y轴负向的匀强电场。质量为m、电荷量为q的带正电粒子由正方形区域Ⅰ的顶点A以初速度v0沿x轴正向射入区域Ⅰ,离开电场后打在区域Ⅱ底边的中点P。若在正方形区域Ⅱ内施加垂直坐标平面向里的匀强磁场,粒子将由区域Ⅱ右边界中点Q离开磁场,进入区域Ⅲ中的电场。不计重力,求:

图1
(1)正方形区域Ⅰ中电场强度E的大小;
(2)正方形区域Ⅱ中磁场磁感应强度的大小;
(3)粒子离开三角形区域的位置到x轴的距离。
【解析】(1)由带电粒子在区域Ⅰ中做类平抛运动可知
设离开电场时与水平方向之间的夹角为θ,则
离开区域Ⅰ后做直线运动
(2)由粒子在磁场中做匀速圆周运动可知
在第(3)问情景中初速度和力不在同一条直线上,粒子做典型的类斜抛运动,由于有三角形区域的限制,属于受限制的类斜抛运动。受斜上抛运动的影响,学生往往只知道把此运动分解成水平的匀速运动和竖直的匀减速运动,实际上合运动和分运动是一种等效替代的关系,已知分运动求合运动解是唯一的,已知合运动求分运动解有无数个,当然在实际的过程中不能随意分解,但是能解决问题的分解方式往往不止一种,由于力和速度都是矢量,分解力或者速度都是可以的,下面我们从不同的角度分析此类问题。
(3)解法一 把速度向力的方向和垂直于力的方向分解


图2
解法二 把力向速度方向和垂直于速度方向分解


图3
解法三 既不分解力也不分解速度


图4
解法四 逆向思维


图5
在上述的四种方法中都用到了运动的分解,前三种方法大同小异,第四种方法有别于前三种,它是一种求异思维,是逆着事物发展方向的分析方式,是一种重要的思想方法,需要对事物的发展有深刻的认识。在上述问题的分析中四种方法没有明显的优劣之分,只是提高了创新思维能力和发散思维能力,增加了分析问题、解决问题的角度,但是在有些问题中方法不同,解决问题的难易程度明显不同,下面我们分析一道关于类斜抛运动中的极值问题。
二、类斜抛运动中极值问题的优化处理
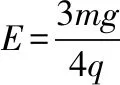

图6
(1)小球由A运动至B的时间t;
(2)竖直墙面BC的高度h;
(3)小球从B点抛出后,经多长时间动能最小?最小动能是多少?


(3)解法一 把运动沿水平和竖直方向分解
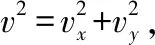

图7
解法二 把运动沿合力和垂直于合力方向分解
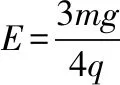
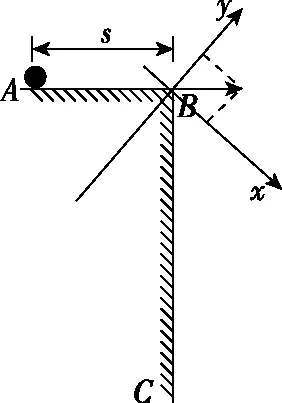
图8
在上述的两种解法中虽然都用到了运动的分解,但在解法一中分解之后还要再合成、还要讨论关于时间t的二次函数极值以及对应的条件,而在解法二中通过运动的分解很容易得到极值条件以及对应的极值,简化了数学讨论,优化了解题的过程。
三、结束语

