活跃在各级考题中的三角形三正切公式

甘肃

本文以一道省级数学联赛试题为例，通过对不同解法的比较，揭示了试题命制的背景，以三正切公式为载体的内在关联.并且通过在不同的竞赛试题中的应用，进一步表明了三正切公式是各级竞赛试题中联系三角和代数之间的重要桥梁和纽带.

题目(2018·全国高中数学联赛(吉林)预赛·6)设x>0，y>0，z>0，满足x+y=xy，x+y+z=xyz，则z的取值范围是

( )

分析这是一道有限制条件下的多元函数的最值问题，多元函数的变量多，式子复杂，其解决方法主要是消元法，将其转化为一元函数的最值问题，然后运用函数的思想或者基本不等式来解决.

解法1 整体消元法

由x+y=xy，x+y+z=xyz得xy+z=xyz，

解法2 代入消元法

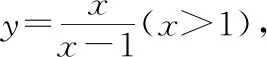
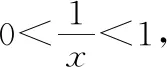
注意到题设限制条件x>0，y>0，z>0，且x+y+z=xyz的结构特点，结合在斜三角形中三个内角满足tanA+tanB+tanC=tanAtanBtanC，可以做三角代换.如解法3所示.

解法3 三正切公式

在锐角三角形ABC中，令x=tanA，y=tanB，z=tanC，

则tanA+tanB+tanC=tanAtanBtanC，

又由x+y=xy得tanA+tanB=tanAtanB，

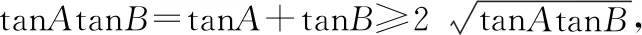
所以tanAtanB≥4，(1)

评析多元问题的解决方案主要是消元，但本题根据已知条件的结构特点，转化为锐角三角形中的有关问题，这正是这道多元函数最值试题命制的背景，三个变量之间的相互制约的关系实际上是锐角三角形三个内角正切值之间的联系.用三角代换解答该问题，不落俗套，令人耳目一新.

在解法3中，根据试题特点，用到了斜三角形三个内角的正切函数之间满足的一个恒等式，即tanA+tanB+tanC=tanAtanBtanC，这是苏教版必修4P104例4的结论，实际上是在任意非直角三角形中和角正切公式的变形，由于含有三角形三个内角的正切函数，且为了下面行文方便，不妨称之为三角形的三正切公式，以这个三角恒等式为背景命制的试题活跃在近年各级考试当中，尤其受到各级竞赛命题者的青睐.

1 恒等式的证明

因为在斜三角形ABC中，tanA,tanB,tanC都有意义，

tanA+tanB=-tanC(1-tanAtanB)，

移项整理得tanA+tanB+tanC=tanAtanBtanC.

推论当A+B+C=kπ(k∈Z)，且tanA，tanB，tanC有意义时，始终有tanA+tanB+tanC=tanAtanBtanC.

tanA+tanB=-tanC(1-tanAtanB)，

移项整理得tanA+tanB+tanC=tanAtanBtanC.

2 直接考查三正切公式

例1(2017·全国高中数学联赛(河北)预赛·10)在△ABC中，角A，B，C所对的边分别为a，b，c，有等式lntanA+lntanC=2lntanB.

(1)求证tanA+tanB+tanC=tanAtanBtanC；

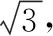
解：(1)证明过程略；

(2)由已知条件，tanA>0，tanB>0，且tanC>0，△ABC为锐角三角形.

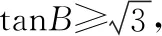
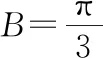
评析本题第(1)问直接考查了三正切公式的证明，第(2)问根据已知条件，运用三正切公式结合三元均值不等式求出了角B，进而转化成了一个三角形中的定角对定边问题的变化试题.

3 直接应用三正切公式

例2(2016·江苏卷·14)在锐角三角形ABC中，若sinA=2sinBsinC.则tanAtanBtanC的最小值是________.

解：因为sinA=2sinBsinC，所以sin(B+C)=2sinBsinC，

展开得sinBcosC+cosBsinC=2sinBsinC，

两边同除以cosBcosC得tanB+tanC=2tanBtanC，

(当且仅当tanA=2tanBtanC时，取“=”)，

所以tanAtanBtanC的最小值是8.

例3(2018·江苏宿迁市高三第一学期期中考试·14)在锐角△ABC中，9tanAtanB+tanBtanC+tanCtanA的最小值为________.

解：在△ABC中，tanA+tanB+tanC=tanAtanBtanC，两边同除以tanC得

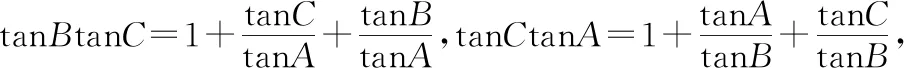
9tanAtanB+tanBtanC+tanCtanA

=25.

解：在△ABC中，由sin2A+sin2C=2 018sin2B得a2+c2=2 018b2，

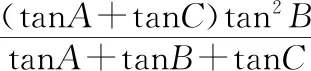
4 构造三正切公式

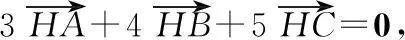
因为H是△ABC的垂心，所以a·b=a·c=b·c，

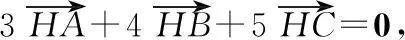
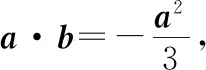
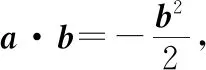
cos∠AHB=cos

也可根据三角形垂心的特点，构造三正切公式，转化为三角问题，如解法2所示.

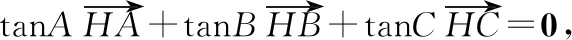
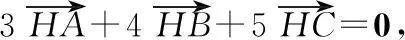
由tanA+tanB+tanC=tanAtanBtanC，

评注解法2依据三角形的垂心满足的特点，构造出该题满足三正切公式所需条件，把一个较为复杂的向量问题，转化为三角问题，从而简化了运算.

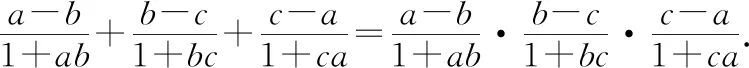
分析左边是三个分式的和，右边是与左边相同的三个分式的积，符合三正切公式的特点，另外，三个分式都符合两角差的正切公式，从而明确本题证明方向为三角代换.

证明：令a=tanA，b=tanB，c=tanC，

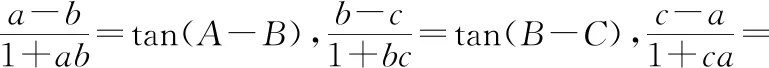
tan(C-A)，

且(A-B)+(B-C)+(C-A)=0·π，

所以根据推论得，tan(A-B)+tan(B-C)+tan(C-A)=tan(A-B)·tan(B-C)·tan(C-A)，

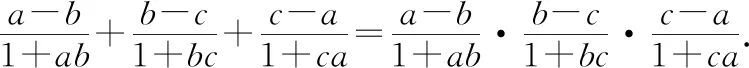
评注本题的证明依据推论，要验证(A-B)+(B-C)+(C-A)=0·π.

5 其他应用

根据正弦定理得sinAcosB=4sinBcosA，

即4tanB=tanA.

又tanC=-tan(A+B)

在斜三角形中，tanA+tanB+tanC=tanAtanBtanC，

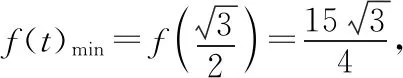
6 解题感悟

从解题的角度来看，将三角形式的题目转化为代数问题，解答方法就丰富起来，而把代数问题转化为三角问题，可以利用三正切公式，使解答变得方便快捷，三正切公式是把解三角形中的有关问题与代数问题联系起来的纽带之一.

从命题的角度来看，根据试题结构特点，对于本文开头题目可以改编成一个纯粹的三角问题：在锐角三角形ABC中，若tanA+tanB=tanAtanB，求tanC的取值范围.而对2016江苏高考第14题这个三角试题，也可以改编为一个纯粹的代数试题：设x>0，y>0，z>0，满足x+y+z=xyz，x=2yz，则xyz的最小值为________.经过改编，前者条件明确，具有了高考试题的特点，后者条件隐晦，具有了竞赛试题的特点，这种改编，体现了高考试题和竞赛试题之间的转化，也体现了数学不同章节之间的联系，使得解答方法多样化，揭示了试题隐含的背景，这也许是三正切公式在各级竞赛中频繁出现的一个原因.