轨道交通施工对地面的影响及其沉降变形监测
2019-08-02
(成都理工大学 四川 成都 610000)
当城市轨道施工进行盾构施工或者开挖基础时,会对周围和上方的土体的土应力发生不可避免的影响,导致路面上方或周围地形发生形变,有可能产生安全隐患或者发生塌方等危险。本文配合各大城市轨道交通的技术规范,重点研究城市轨道交通的建设对于原有城市路面的影响,以及对城市路面进行沉降变形监测以发现其形变规律并对其进行预测及其预警。
一、变形监测和沉降变形监测
变形监测是对被监测变形体进行测量来确定它的空间所在位置和它内部形态随着时间变化的变化特性,又称为变形观测。在本文中,变形体指城市用于轨道施工的城市原有地面,研究其在轨道交通施工中因荷载的加重或者土应力改变造成的沉降变形。
沉降变形监测为变形监测中的一项重要监测内容,在许多的文献资料中也叫做垂直位移监测或者沉降监测。实际施工的过程中,沉降表达的是一种向量,由于土应力的变化,建筑物体也可能出现上升的态势,也同样对建筑成果产生危害和安全隐患。所以在赋值时,差值为“+”时表示建筑物或者被监测物体的“下沉”,差值为“-”时表示建筑物或监测物体的“上升”。
二、沉降变形监测的数据处理
(一)监测数据的预处理。室内核检工作分为原始控制数据的统计分析,原材料的检验,第一次数据的逻辑分析。如果当监测分析结果与真实值存在较大偏差时其可能的原因为出现大误差或者粗差或监测体确实出现了较大的形变。
(二)监测网的数据处理。在监测网的数据处理中选择平均间隙法进行处理,平均间隙法通过整体检验和不稳定点搜索这两个步骤来确定整个监测网络是否稳定。
整体检验。采用某两个周期的成果数据进行的稳定性检验,按照自由网平差的方法进行平差,得出平差改正数后则可以计算单位权方差的估值,如果两周期观测点位没有变动,那么可以从这两个周期的坐标差 来计算另一方差的估值,利用F检验法,可组成统计量,再采用公式
P(F>F1-α(fΔx,f)/H0)=α
来检测点位是否有变动,一般取0.05或0.01。当F小于相应分位值时,则认为点位是稳定的,如果大于相应分位值时,则认为两次周期观测变换了位置然后采取第二步搜索不稳定点。首先把数据分为稳定组和不稳定组,分别用W和B表示,稳定组里也可能有不稳定点,通过对稳定点的图像的表现来检验稳定组里是否含有不稳定点。公式如下所示:
如果W1 (三)监测点的数据处理。变形监测点是数据的最基本的组成部分,在此文中将利用回归分析法来解决监测点的数据处理问题。 回归分析法是处理变量之间的关系的一种方法,是属于数理统计范畴的一种运算形式,把我们所观测的观测物体作为所研究的一个系统,按照系统分析的方法,对变形体的各种变量,包括温度湿度荷载等输入进系统内部,作为自变量,将输出的数值作为系统所在的因变量,通过对变形物体的长时间重复的大量观测,可以大体的估算出其变形物体的形变量和变形因素之间的函数关系,通过函数的体现来预测未来的形变情况,从而进行变形预报。 回归分析是研究因变量和很多个自变量之间的关系的过程。它的数学模型为 yt=β0+β1xt1+β2xt2+...+βpxtp+ξt 建立回归方程y=xβ+ε,可以求得 因为之前的回归方程不能确定是否y与x之间有无关系所以我们应对方程进行显著性检验。我们假设不存在线性关系,则β为零向量,可求得统计量 如果假设成立,则F应当服从F(P,n-P-1)分布,则用下式检验 p{|F|≥F1-α,p,n-p-1|H0}=α 如果上式符合要求,则回归方程式的显著性就可以确定了。 回归系数显著性的检验。在回归方程中,并不是每一个自变量都能够和因变量有着显著地影响,所以我们要剔除一些无用的或者影响效果不大的变量,此后建立一个更为简单的回归线性方程,这个过程就用到了回归系数显著性检验的方法。如果方程中的自变量对于因变量的作用不明显,那我们就设这个变量系数βj为零,那么假设为H:βj=0,由模型求得 则检验假设的统计量为 (四)粗差检验与精度评定。在数据处理时,有些粗差我们难以判断,所以我们利用统计学的范畴解决此类问题。我们把正态分布规定在一个区域,正态分布无限的接近于这两个临界值,如果数值超过此临界值,那我们则认为超出临界值的数值为粗差。应当给于剔除。可以使用莱茵达(3S)准则来进行粗差的剔除,原理为对某监测物观测重复观测m次,如果观测误差大于三倍标准偏差S时,则认为该数值为粗差,应给与剔除。 本文通过传统的变形监测和轨道交通施工的关系系统的给出了地下轨道交通施工对路面沉降影响和具体的数据处理流程,对以后城市轨道交通施工提供一定的理论帮助。通过此方法对某地的轨道交通施工变形监测后发现,轨道交通的建设尤其地下线路的建设还有具有一定的影响,因为路面以上修建架桥或者地下开挖隧道的原因,导致地面的荷载增大或者土应力变大,使城市表面路面出现变形沉降。对于此种方法,缺点在于需要大量的数据作为支撑,并且对数据的精度要求较高,可能需要涉及到整条线路的建设周期,对于人力物力的要求是一个不小的挑战,也是未来此类方法的重点研究方向。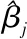
四、结论
