基于人体敏感频率的二自由度动力吸振器研究

孙 煜，周劲松，宫 岛，孙文静，夏张辉

(同济大学铁道与城市轨道交通研究院， 上海 201804)

列车运营速度的提高意味着更严重的振动，这就要求铁路运输从振动对人体生理影响出发，开展改善舒适度的研究[1]。振动是不舒适的来源，人处于振动环境中，不仅会引起疲劳，还可能发生人体内部器官及全身组织与外界振动共振的可能。为此，诸多学者对车辆振动控制展开研究，文献[2-3]建立了铁道车辆路-车-人统一的数学模型，运用协方差算法计算车辆运行平稳性，提出了基于车体模态参数来评估与分析车辆运行品质的方法。文献[4-5]提出将车下设备设计为车体的动力吸振器，以降低车体弹性振动，从而提高车辆运行平稳性。文献[6]提出将构架纵向振动设计为车体垂向弯曲振动的动力吸振器，通过数值仿真分析和实验研究，证明了所提出的方案可以有效降低车体振动。文献[7]将车体视为均质欧拉-伯努利粱，在车底纵向安装抗垂弯减振装置，从而改变一阶垂弯频率，以降低车体垂向弹性振动，但所提出的抗垂弯减振装置重量较重、长度大，工程运用难度较高。

以往车体振动控制研究中，大多是抑制车体弹性振动，鲜见抑制车体刚性振动的研究。本文基于平稳性指标权重函数，结合高速动车组实测数据，提出采用基于加速度的二自由度动力吸振原理，设计同时抑制车体浮沉与点头振动的二自由度动力吸振器，建立高速动车组动力学模型，运用虚拟激励法及运行平稳性协方差算法计算二自由度动力吸振器对高速动车组运行工况下车体振动的影响。研究表明，安装二自由度动力吸振器后，车体响应功率谱密度峰值明显降低，车辆运行平稳性提高，二自由度动力吸振器可有效抑制车体浮沉及点头振动。

1 平稳性指标权重函数

国内某型高速动车组速度为300 km/h时的车体中部垂向加速度功率谱密度如图1所示。实测结果显示，车体垂向振动加速度主频为2.0 Hz，该振动是由于车体浮沉振动所致，除主频外，在9.25 Hz处也有一个峰值，此峰值是由于车体弹性一阶垂向弯曲振型所致。可以看到，弹性振动所致峰值明显小于刚性振动所致峰值，即弹性振动能量小于刚性振动能量。

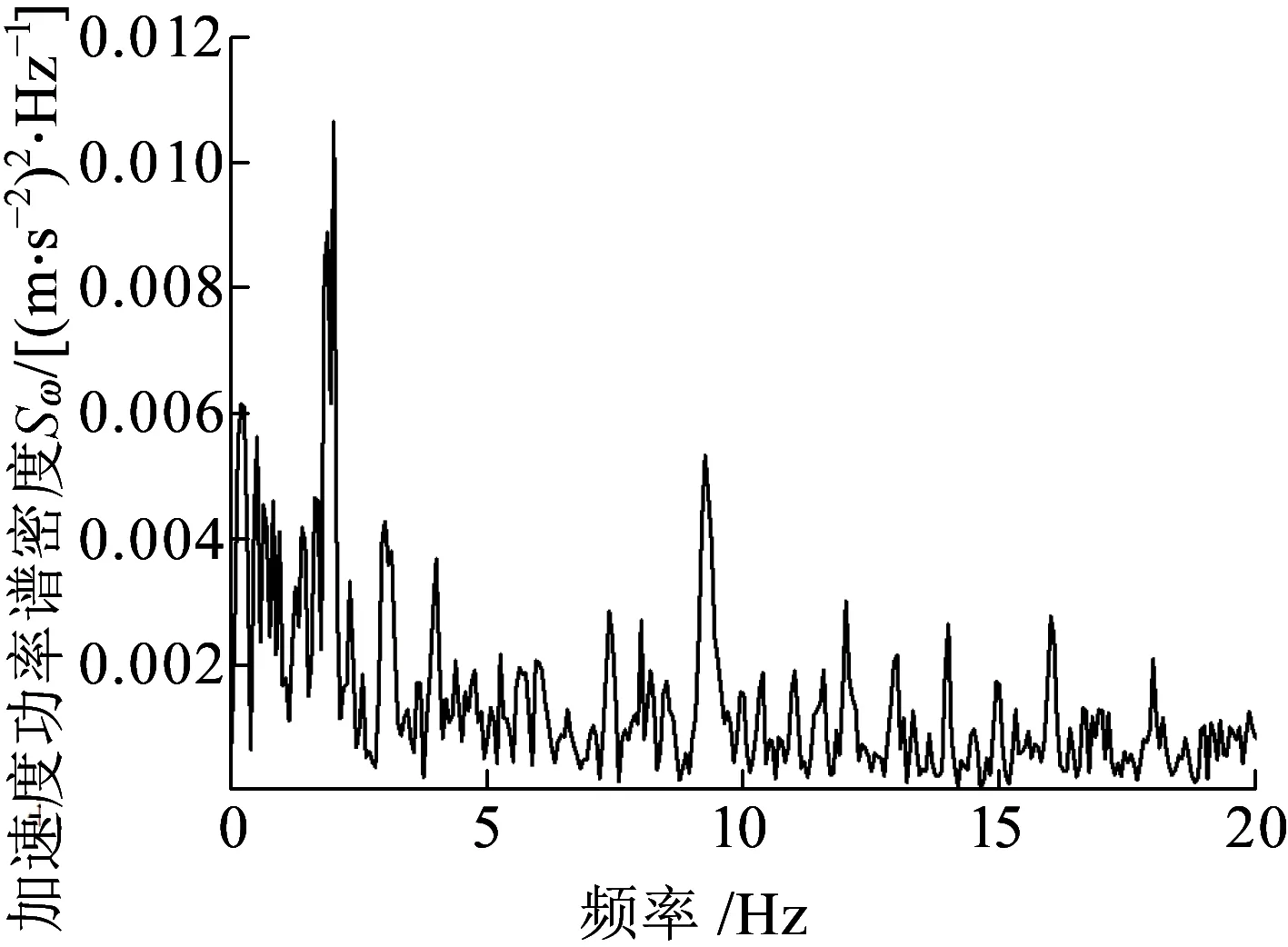
图1 实测车体中部垂向加速度功率谱

合理的动力学性能评价方法与适当的指标体系是对车辆动力学性能评价的重要依据，目前我国采用GB/T 5599—85《铁道车辆动力学性能评定和试验鉴定规范》[8]进行铁道车辆动力学性能评价，其中对车辆运行品质的评价采用的是平稳性指标Wz，该指标可依据连续单一权重函数和相应积分算法一次性获得。其中，用于垂向舒适度评价的权重函数Bs为[9]

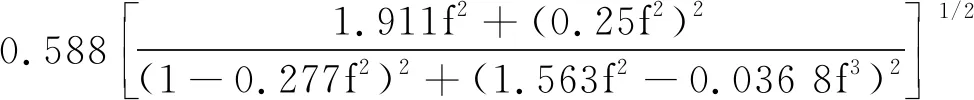
(1)

式中：f为振动频率。权重函数反应的是人体对各频率的敏感程度，权重函数越大，代表人体对该频率越敏感。根据式(1)绘制其幅频特性如图2所示。可以看到，车体刚性振动所在的2.0 Hz处权重函数明显高于弹性振动所在的9.25 Hz。以往的研究大多是对车体弹性振动进行控制，鲜见对车体刚性振动进行控制。结合图1与图2可以发现，从人体感受舒适度的角度出发，对车体刚性振动进行控制具有更加重要意义。

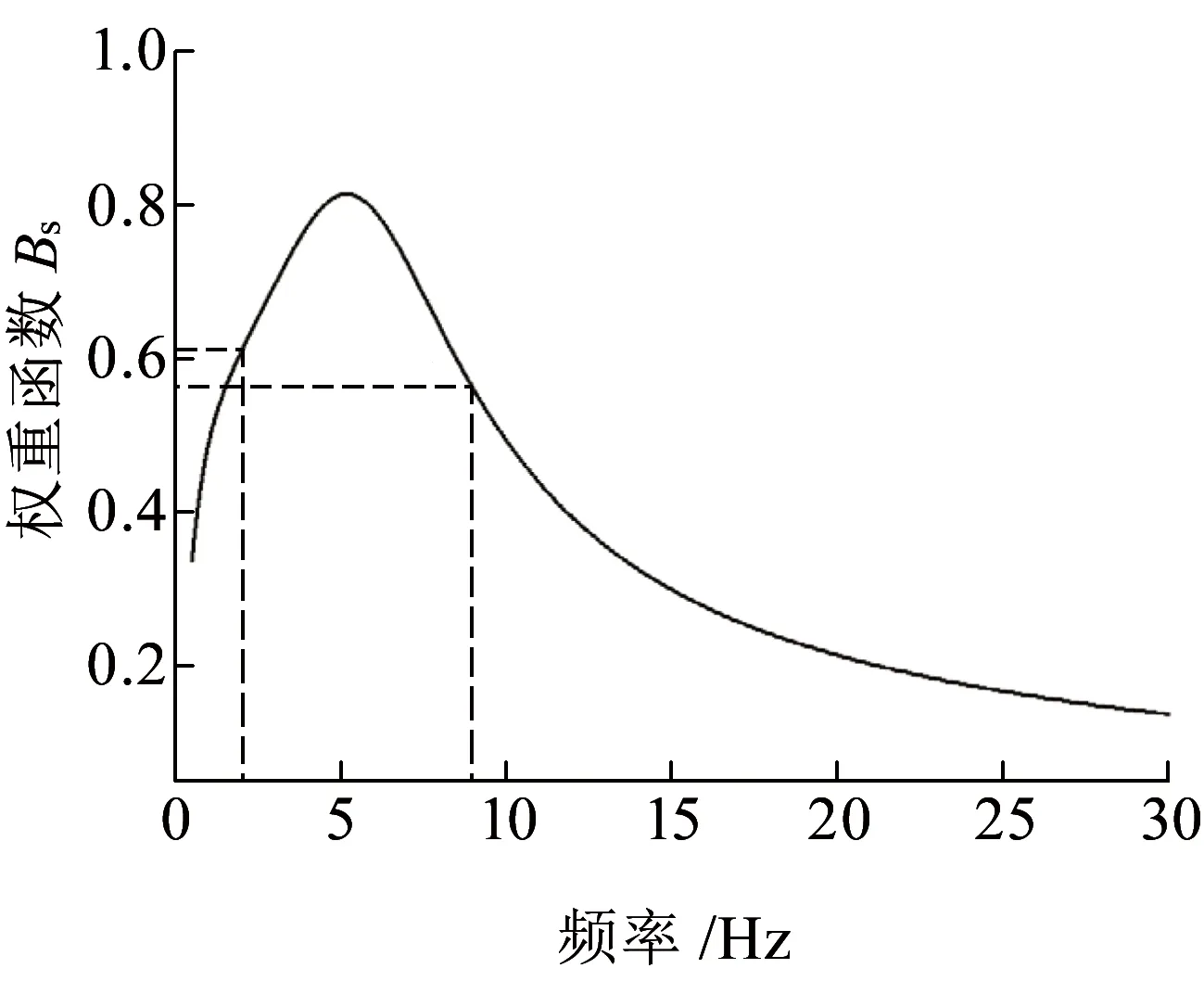
图2 平稳性指标权重函数

2 基于加速度的二自由度动力吸振原理

动力吸振器是一种被动振动控制方式，在桥梁、航空等工程领域得到广泛运用。其工作原理是在振动物体上安装附加质量、弹簧、阻尼系统，使系统在振动时，辅助系统产生与主系统振动方向相反的力，从而降低主系统的振动[10]。

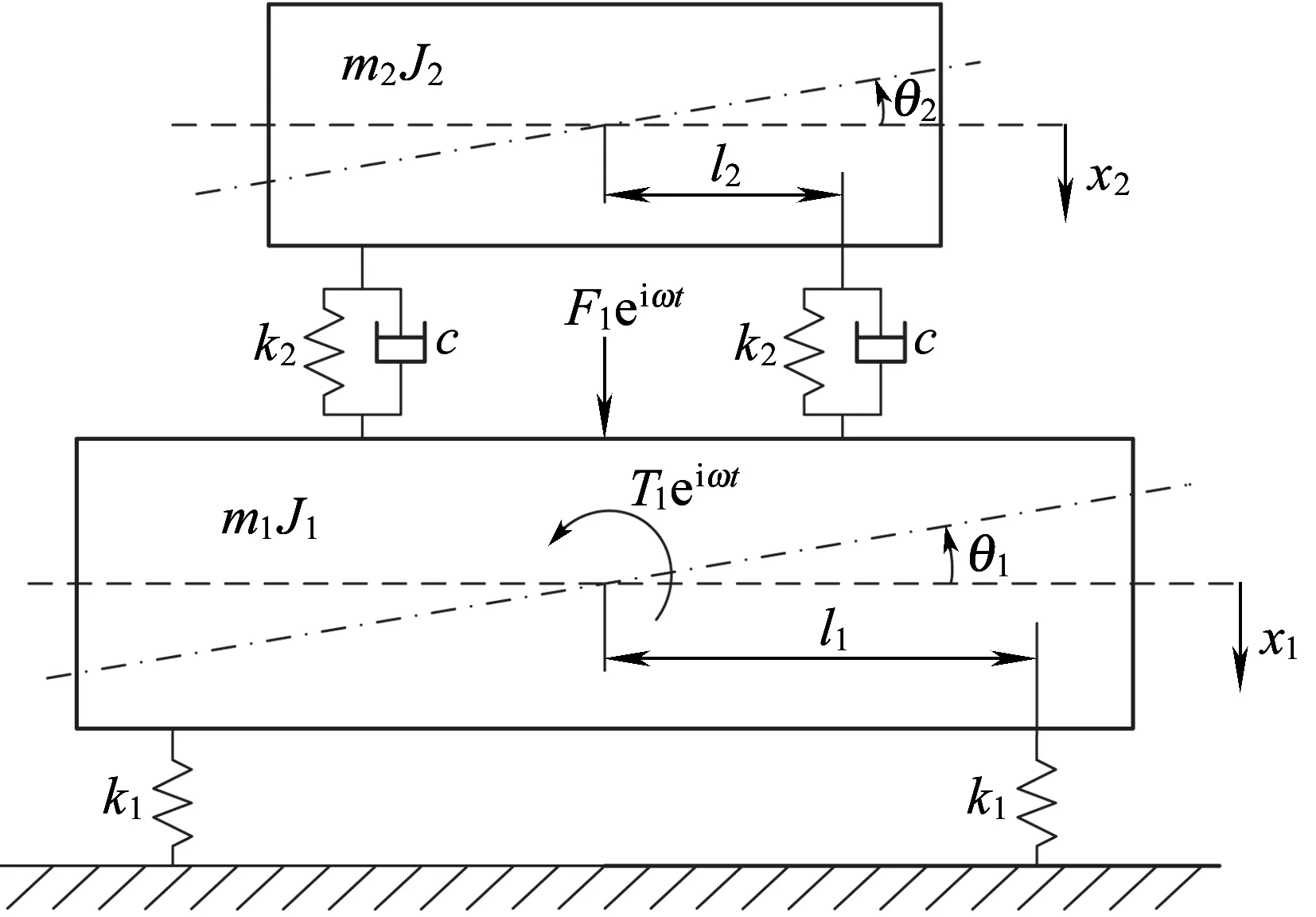
图3 二自由度动力吸振器原理图

图3是二自由度动力吸振原理图，主振动系统及动力吸振器系统均考虑了浮沉和点头振动，其动力学方程为

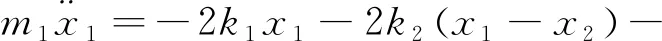
(2)

(3)

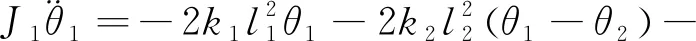
(4)

(5)

式中所涉及参数及其意义见表1。

表1 二自由度吸振器参数及其含义

通过观察模型的振动微分方程可以发现，浮沉振动和点头振动并不耦合，相互独立。也就是说，两种振动可以单独进行描述。本文以点头振动为例，推导基于加速度的点头吸振原理，联立式(4)与式(5)，假设其解为

(6)

式中：Θ1、Θ2分别为主振动系统和动力吸振器的响应幅值；φ为相位。主振动系统的加速度可表示为

(7)

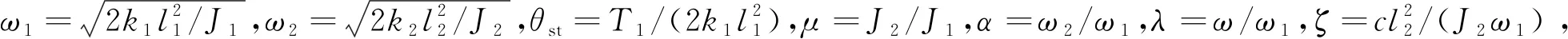
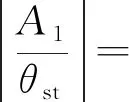
(8)

利用定点理论，令式(8)中ζ=0及ζ=∞的两式相等，计算可得两定点的坐标表达式，再令二者等高，可得满足加速度响应的动力吸振器最优同调条件为

(9)

基于加速度响应的最优同调得到满足时，主振动系统加速度响应与定点P、Q的关系如图4所示，图4所示是转动惯量比μ=0.1的情况，其中ζ=0.18是动力吸振器最优阻尼，此时主振动系统加速度响应振幅比峰值位于定点P、Q附近。

图4 主振动系统加速度响应曲线

3 车辆垂向动力学模型的建立

由于铁道车辆垂向和横向动力学存在弱耦合，所以通常分开建模进行研究。车辆垂向力学模型如图5所示。建模时，轮对、构架、车体、动力吸振器均假设为刚体，不考虑轨道弹性。车辆运行中，假设车轮始终贴靠钢轨，也就是说，建模时不考虑轮对的垂向运动方程，这样车辆垂向动力学模型为8个自由度，分别为车体、动力吸振器及前、后转向架的浮沉、点头(2×4)。

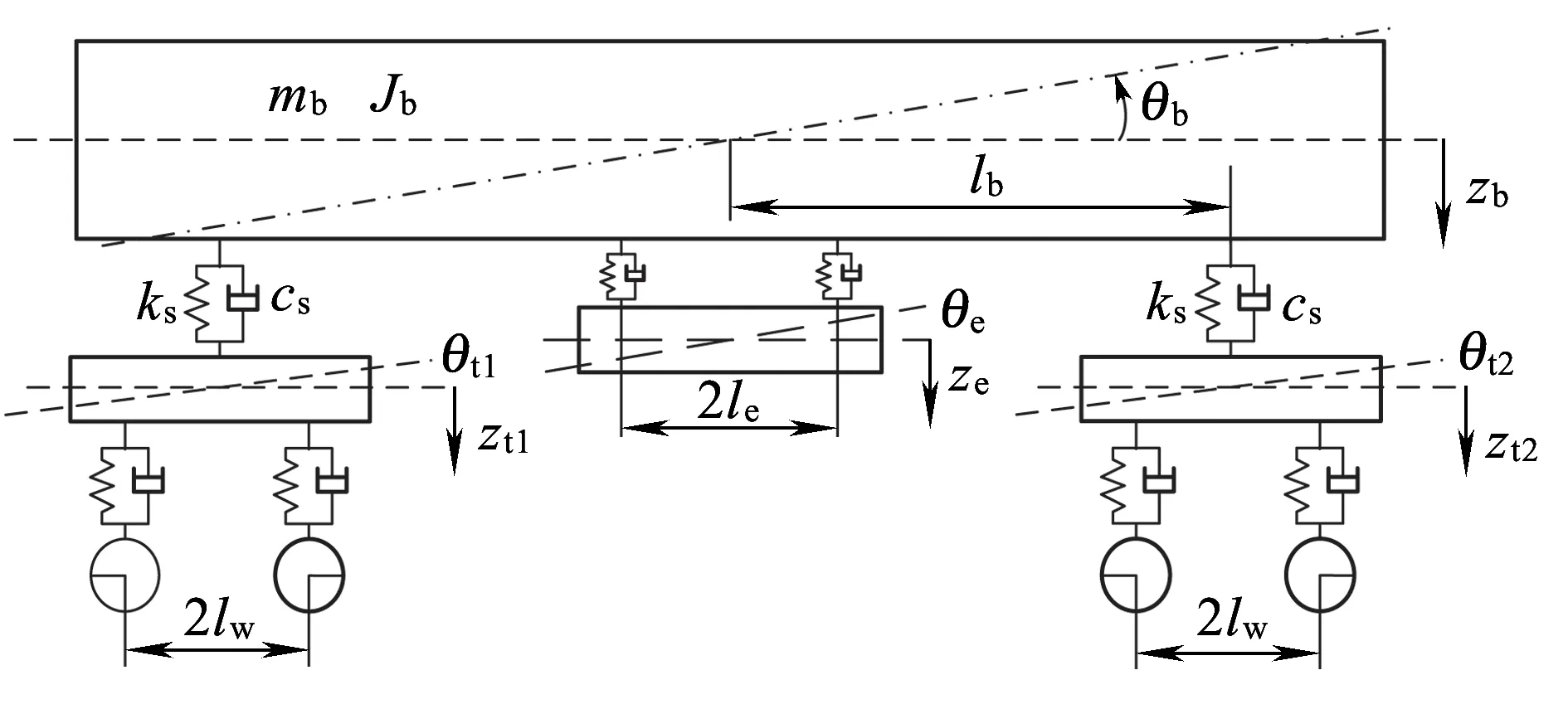
图5 垂向力学模型

根据图5所示单车垂向力学模型，列车动力学方程为

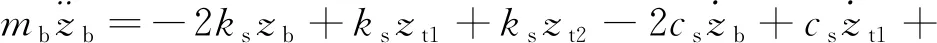
(10)

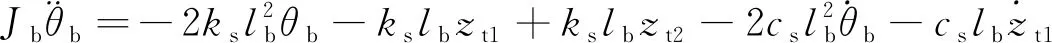
(11)

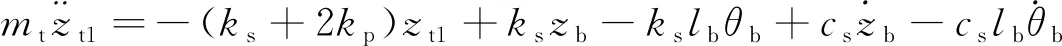
(12)

(13)

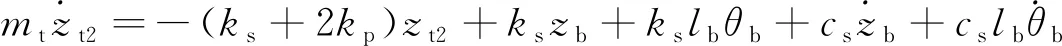
(14)

(15)

(16)

(17)

式中各参数及其意义见表2，参数取自某型高速动车组。

表2 车辆动力学参数及其含义

上述可以表示为

(18)

其中

(19)

(20)

式中：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；Dw为激励输入矩阵。将式(18)写成状态方程形式

(21)

其中

(22)

无动力吸振器车体振型频率及阻尼比见表3。

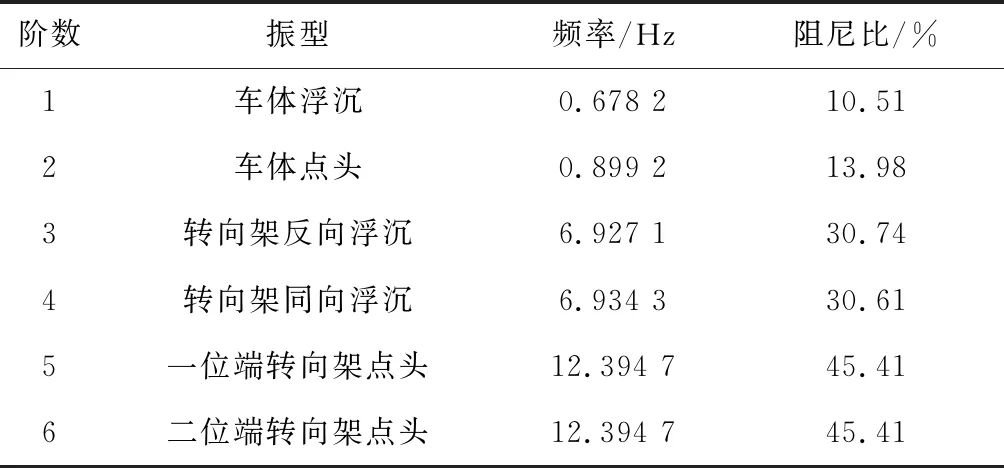
表3 车体振型频率及阻尼比

4 虚拟激励分析方法及运行平稳性协方差算法

运用虚拟激励分析方法[11-13]可以快速获得铁道车辆系统的响应幅值谱。对于轨道车辆系统而言，第2～4位轮对的输入可视为第1位轮对输入的时延，将f(t)视为广义的单激励，设F(t)的自谱密度为SFF(ω)，则对于4点异相位平稳随机过程的虚拟激励为

(23)

将式(23)带入式(18)可得

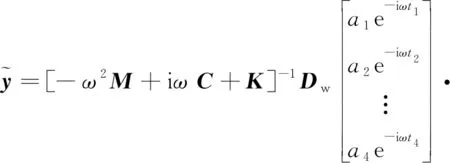
(24)

于是可得响应功率谱Syy为

(25)

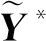
平稳性协方差算法没有时域积分过程，只通过矩阵运算就可以获得线性模型的平稳性指标[14-15]，计算速度快，效率高。对于式(21)的铁道车辆动力学状态方程，当输出为

Y(t)=CX(t)

(26)

系统状态向量的协方差矩阵为

Xxx(t)=E[X(t)X(t)T]

(27)

该矩阵为稳态值，为Liapunov方程的解

AXxx+XxxAT+Q=0

(28)

式中：Q为B和Zww的函数。输出变量的协方差矩阵为

Yyy=E[(Y(t)Y(t)T)]=CXxxCT

(29)

采用协方差法计算平稳性时，需要经过图6所示的几个环节，其中，成型滤波器用于将白噪声信号滤波，生成轨道不平顺信号；感觉滤波器根据平稳性指标对输出信号进行权重滤波，本文采用式(1)所示权重函数进行计算。

图6 采用协方差法计算平稳性的流程

5 计算研究

采用表2所给参数，轨道不平顺采用高速高激扰谱，运用虚拟激励分析法对上述所建模型进行动力学分析。图7、图8分别为无动力吸振器车体与采用二自由度动力吸振器的车体浮沉、点头加速度响应功率谱，车辆运行速度为300km/h。从图7可以看出，采用二自由度动力吸振器后，车体浮沉振动主频从原来的单峰值变成了双峰值，原浮沉振型频率0.6782Hz处峰值大幅减小。图8显示，采用二自由度动力吸振器后，车体点头振动主频率处峰值得到小幅抑制，但抑制作用不如浮沉明显。

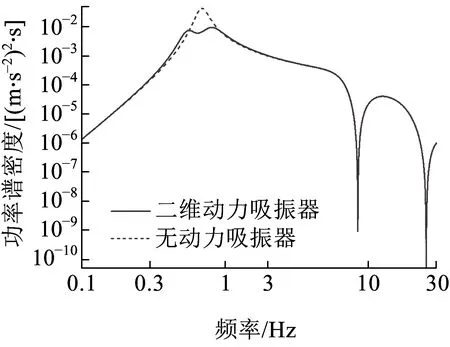
图7 浮沉加速度功率谱密度

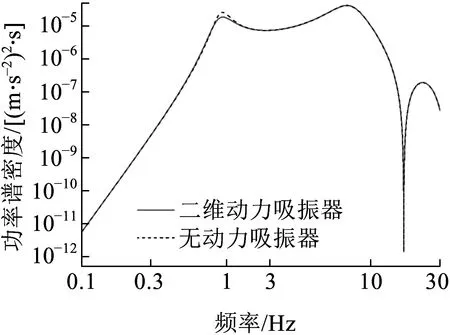
图8 点头加速度功率谱密度

图9、图10分别为无动力吸振器车体与采用二自由度动力吸振器车体在前、后转向架处的垂向加速度响应功率谱。无论是前转向架处还是后转向架处，采用二自由度动力吸振器后，车体低频处共振峰均从单峰值变为双峰值，且振动峰值明显降低，这是由于采用二自由度动力吸振器后，车体浮沉振动、点头振动同时受到抑制的结果。

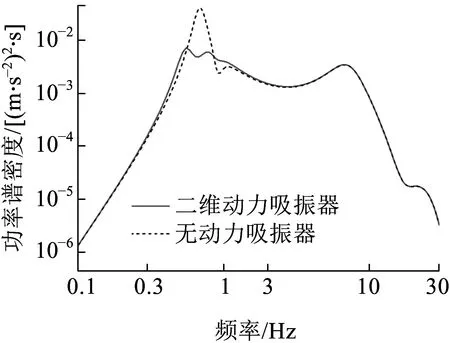
图9 车体前转向架处加速度功率谱密度

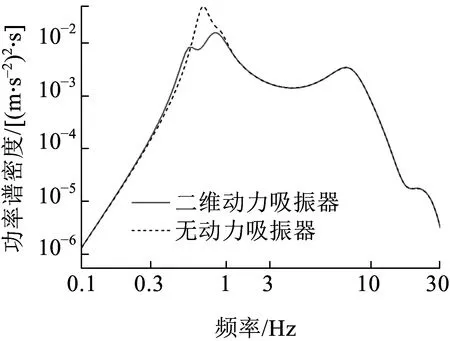
图10 车体后转向架处加速度功率谱密度

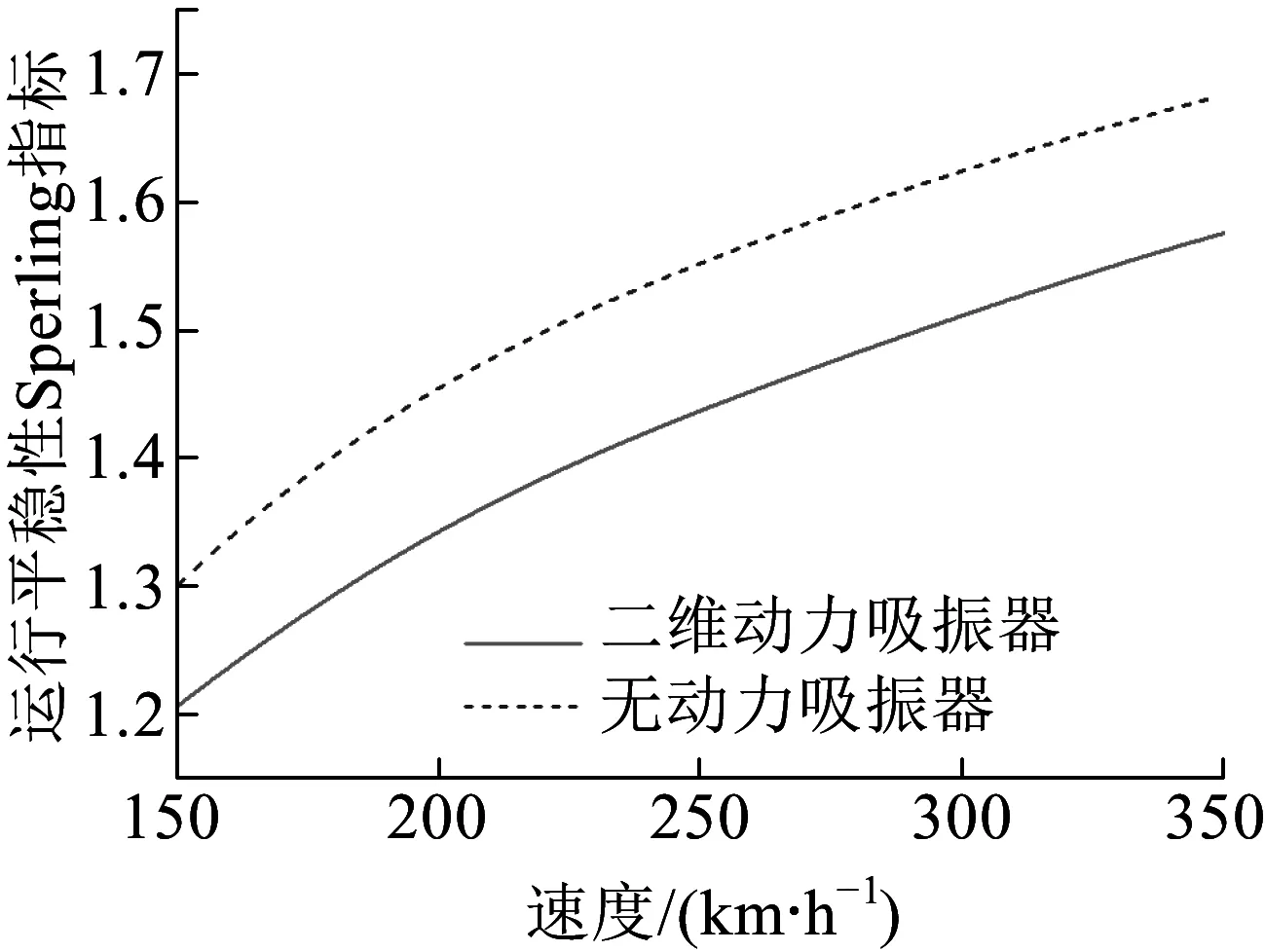
图11 车体中部平稳性指标

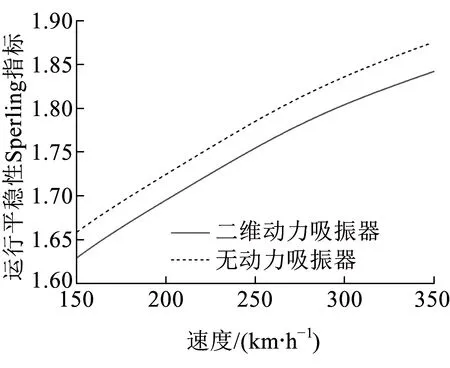
图12 车体前转向架处平稳性指标

图11～图13分别为无动力吸振器车体与采用二自由度动力吸振器车体中部、前转向架、后转向架处的平稳性指标。采用动力吸振器后车体中部、前转向架、后转向架处运行平稳性指标均降低，其中，车体中部降低幅度最大，这是由于采用二自由度动力吸振器后，车体浮沉、点头振动被动力吸振器所抑制，以致车体低频振动加速度幅值降低，从而使运行平稳性得到改善。

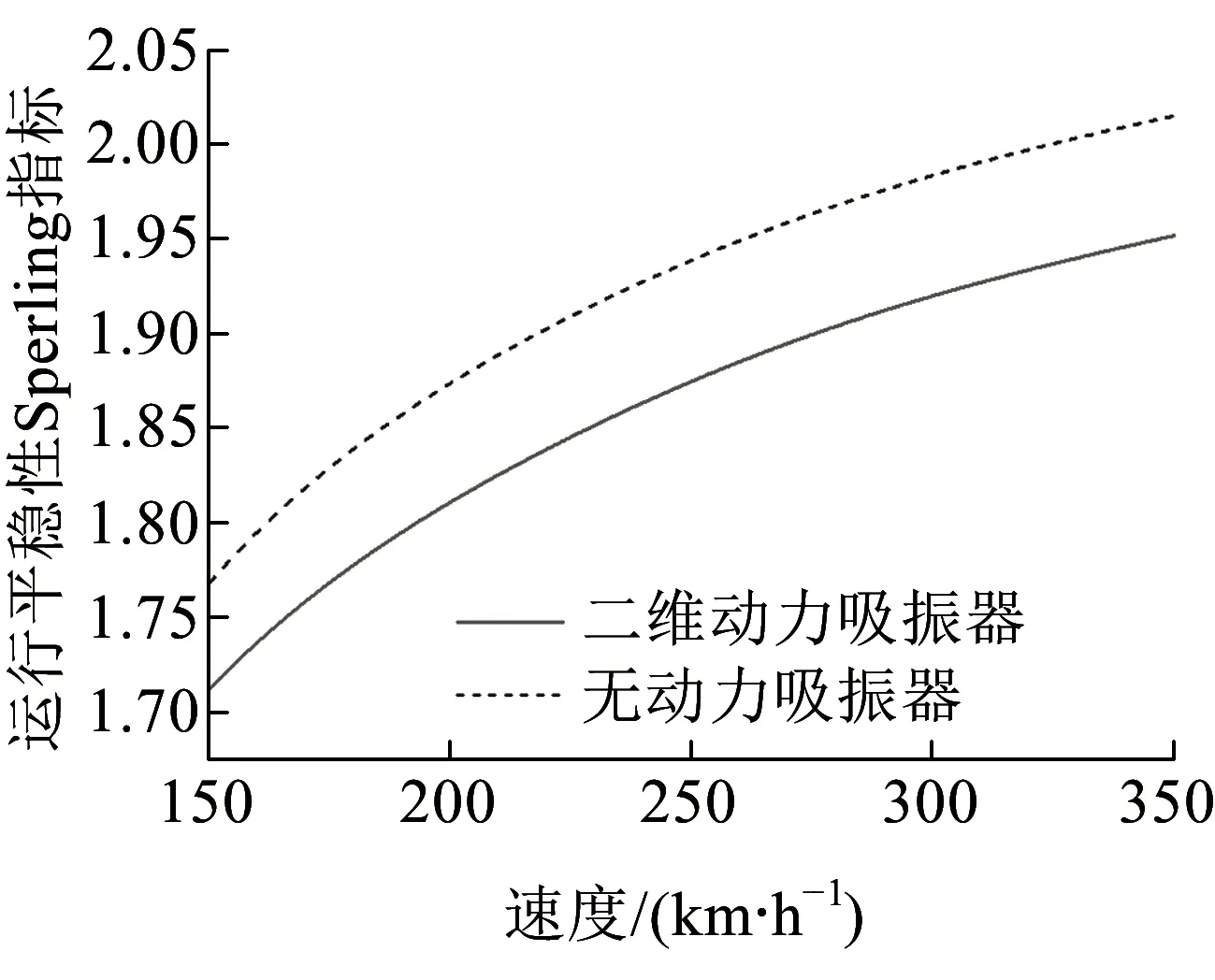
图13 车体后转向架处平稳性指标

将车体视为主振动系统，车下设备视为动力吸振器，对于给定的高速动车组而言，其车下设备质量及转动惯量已经确定，可通过吊挂刚度、阻尼比、吊挂跨距对吸振器浮沉、点头频率、阻尼比进行优化。图14为车下设备与车体质量比μm=0.1时，不同吊挂刚度对车体浮沉振动加速度功率谱的影响，其中吊挂刚度为59kN/m时，车下设备实现浮沉振动最优同调，可以看出，此时车体浮沉振动加速度幅值最小，浮沉振型频率附近的两个峰值基本等高。图15为不同吊挂阻尼比对车体浮沉振动加速度功率的影响，其中吊挂阻尼比为0.22时，车下设备实现浮沉振动最优阻尼，此时车体振动加速度幅值最小。图16为车下设备与车体惯量比μJ=0.1时，吊挂跨距之半对点头功率谱的影响，其中吊挂跨距之半为6.5m时，车体设备实现点头振动最优同调，可以看到，此时车体点头振型频率附近峰值最小。

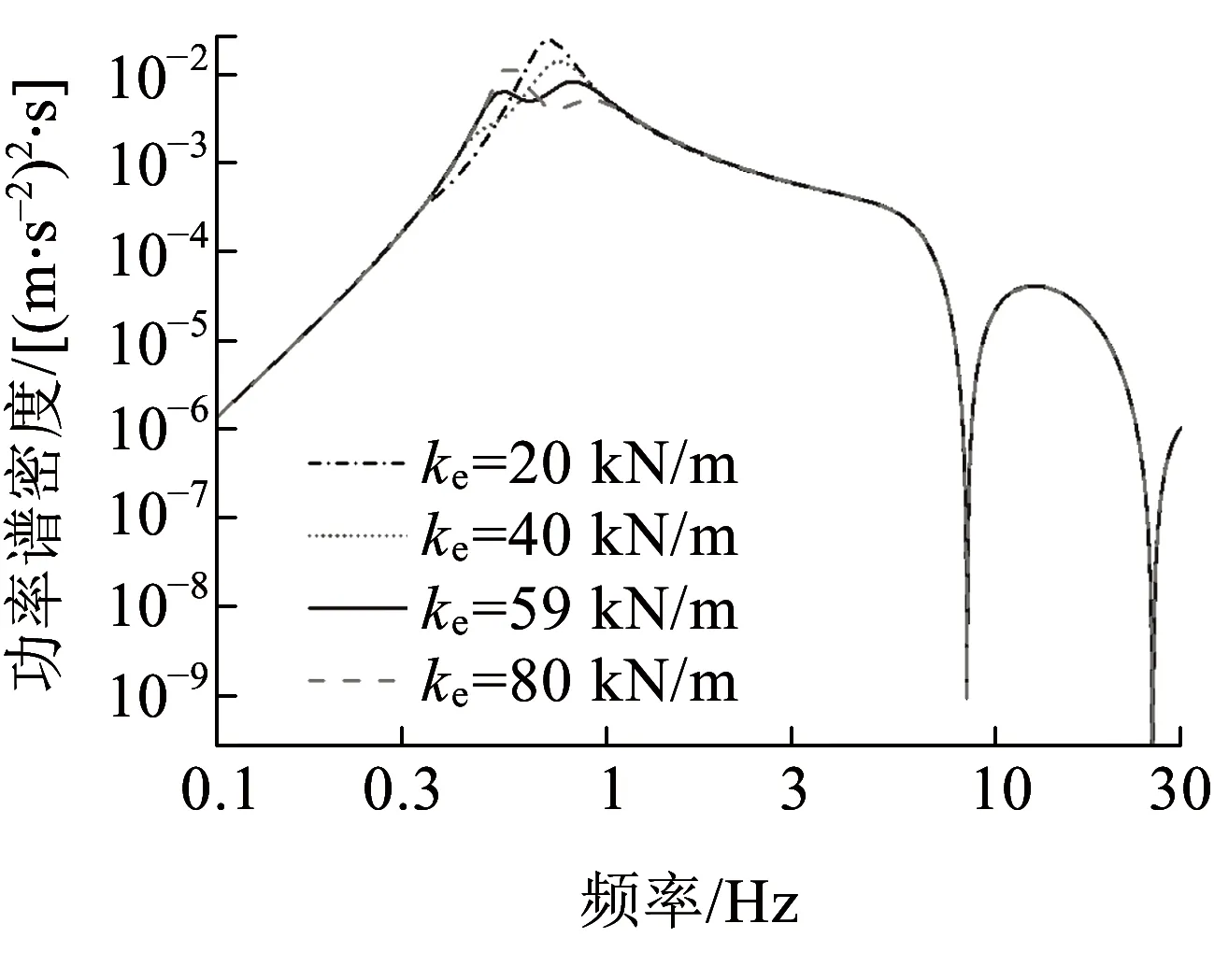
图14 吊挂刚度对车体浮沉功率谱的影响

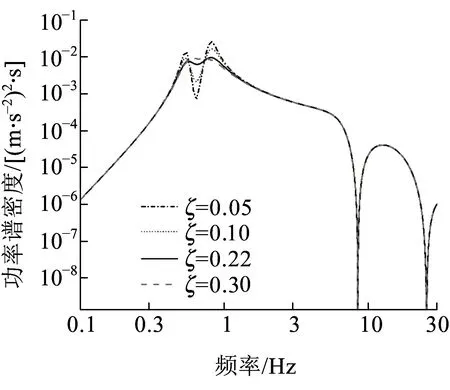
图15 吊挂阻尼比对车体浮沉功率谱的影响

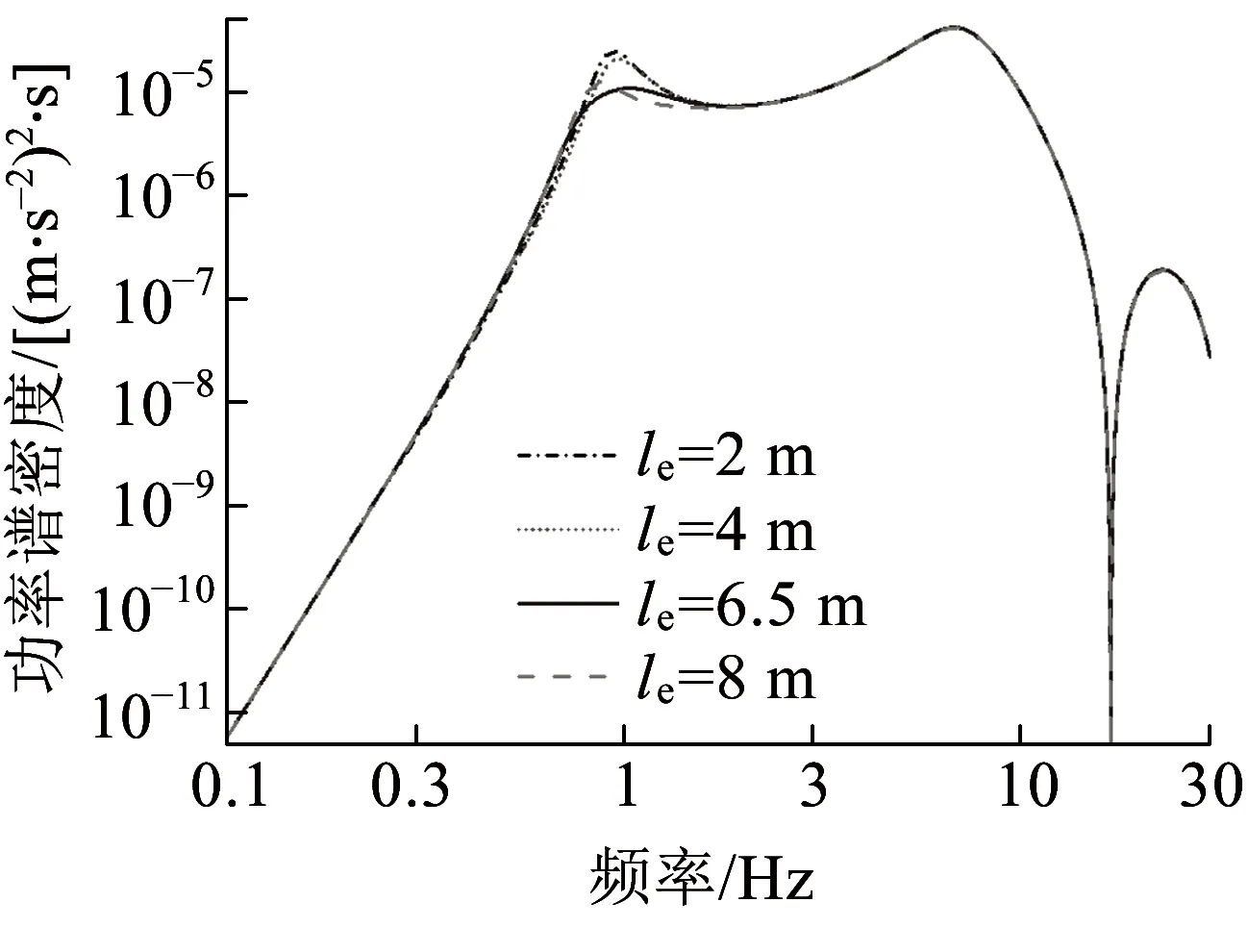
图16 吊挂跨距之半对点头功率谱的影响

6 结论

基于反应人体敏感频率的平稳性指标权重函数，结合实测高速动车组垂向振动加速度功率谱密度，指出对车体刚性振动进行控制的重要性。建立高速动车组垂向动力学模型，采用基于加速度的二自由度动力吸振原理，对车体浮沉及点头振动进行控制，采用虚拟激励法及平稳性快速算法分别计算车体响应加速度功率谱密度及运行平稳性，研究结果表明：

(1)采用二自由度动力吸振器后，车体浮沉振动主频从原来的单峰值变成了双峰值，原浮沉振型频率处峰值大幅减小。

(2)当二自由度动力吸振器实现最优同调、最优阻尼时，对点头及浮沉振动的抑制效果最佳。

(3)二自由度动力吸振器能够有效降低车体浮沉及点头振动，提高车辆运行平稳性。