非对称成对载波多址信号的相位误差分析及幅度改进算法

徐星辰 程剑 唐璟宇 张剑

摘 要：针对由主站和小站信号同频混合而成的非对称成对载波多址（PCMA）信号解调问题，构建了一种实现此类信号解调的框架。参数估计是非对称PCMA通信系统在实现两路信号分离解调时不可或缺的环节，对于幅度参数估计精度问题，提出一种基于四次方法的搜索式幅度估计算法。首先建立非对称PCMA系统解调模型并作出基本假设，然后对不同假设下的相位误差进行对比并分析相位误差对幅度估计算法的影响，最后提出一种新的幅度估计算法。实验结果表明在相同信噪比（SNR）下，正态相位误差下的小站信号解调性能要劣于其均值条件下的解调性能。当误比特率（BER）在数量级为10-4时，改进算法下小站信号的解调性能提升了1dB，说明改进算法优于四次方法。

关键词：非对称;成对载波多址;参数估计;误差分析

中图分类号：TN911.6

文献标志码：A

文章编号：1001-9081（2019）04-1138-07

Abstract： To solve the signal demodulation problem of asymmetric Paired Carry Multiple Access （PCMA） composed of the same frequency of main station and small station signals， a framework to realize this kind of signal demodulation was constructed. Parameter estimation is an indispensable part in the realization of two-way signal separation and demodulation for asymmetric PCMA communication systems. For the estimation accuracy of amplitude parameters， a searching amplitude estimation algorithm based on fourth-power method was proposed. Firstly， the demodulation model for asymmetric PCMA systems was established and the basic assumptions were made. Then the phase errors under different assumptions were compared with each other and the influence of phase error on the amplitude estimation algorithm was analyzed. Finally， a new amplitude estimation algorithm was proposed. Experimental results show that， under same Signal-to-Noise Ratio （SNR）， the demodulation performance of the small station signal under normal phase error is inferior to its demodulation performance under mean value condition. When the order of magnitude of the Bit Error Rate （BER） is 10-4， the demodulation performance of small station signal is improved by 1 dB with the improved algorithm， proving that the improved algorithm is better than fourth-power method.

Key words： asymmetric; Paired Carry Multiple Access （PCMA）; parameter estimation; error analysis

0 引言

1998年，美國Via Sat公司的Dankberg[1]提出了一种基于透明转发器的成对载波多址（Paired Carrier Multiple Access， PCMA）双向卫星通信技术，并申请了自干扰消除技术[2]。该技术提高了卫星信道频带利用率，在节省带宽资源的同时也对信号的解调带来了影响。非对称PCMA通信系统中地面主站接收到由本地信号与小站信号混叠而成的下行混合信号，为实现正常通信，利用主站信号解调后的信息对接收数据再次调制，将主站信号转化为单频分量，然后采用单频干扰抑制抵消算法消除主站信号的影响，以提取小站信号数据[3]。

PCMA系统存在对称和非对称两种工作模式，通过对国内外发展与研究现状的归纳分析能够发现，非对称PCMA研究相对较少。对于非对称模式下PCMA信号的分离解调，文献[4]提出了一种针对同频且功率不同的二进制相移键控（Binary Phase Shift Keying， BPSK）信号的分离方法，利用大信号解调得到的参数对接收信号进行调制，然后在混合信号中消除大信号的干扰，实现小信号的提取;2007年，付迪等[5]针对非对称PCMA信号提出了一种截获方法，同样是对主站强信号直接解调，利用解调信息对强信号进行重构，然后在PCMA混合信号中作干扰抵消以获得小站发送的信息。文献[6]也用类似方法对存在码间串扰和存在同道弱信号干扰的正交振幅调制（Quadrature Amplitude Modulation，QAM）信号进行分离解调。以上方法都是参考多用户检测技术中串行干扰抵消技术进行的扩展应用[7]。

PCMA信号分离解调的目的是实现双方正常通信，非对称PCMA系统中同频混合信号分离大多采用强分离大信号并从混合信号中对大信号进行重构抵消的分离算法，该分离算法需要先对大信号进行信道参数估计，即参数估计是信号分离的关键，各个参数估计误差对系统分离解调性能影响没有明确的研究成果，不利于有针对性地提高分离算法性能，故信道参数估计误差与分离解调性能之间的关系值得进一步深入研究。

本文首先建立了非对称模式下PCMA信号解调的实现框架，接着推导了均值相位误差与误比特率（Bit Error Rate，BER）的关系并进行仿真验证，然后对比分析了动态相位误差对解调性能的影响，最后提出了一种改进的幅度估计算法。

1 非对称PCMA系统模型

非对称PCMA系统是一个自干扰系统，需要进行自干扰信号的抵消后才能进行解调，达到信号分离的目的。非对称PCMA系统解调模型如图1所示，四个待估参数分别为时延τ、载波频率f、载波相位θ以及幅度A[8]。

2.2 正态相位误差设置

本文采用的科斯塔斯环选用二阶数字环路滤波器，为便于分析，不考虑增益变化，只有等效噪声带宽决定滤波器参数的取值，则噪声带宽直接影响环路的性能。为合理设置相位误差值，参考实际工程中的相位偏差。

设置同步头符号速率固定为Rs=2.4ksps，解调门限Eb/N0=5.5dB时，同步头的Es/N0=2.5dB，噪声带宽为符号速率1%，则

由于工程中采用科斯塔斯环跟踪相位会存在随机的相位抖动值，因此取1°、2°和4°为标准差，均值为零，设置相位误差的正态分布集合，将集合中的随机相位误差赋予各个样点，使得信号中误差形式更符合实际。

2.3 仿真分析

2.3.1 均值相位误差仿真

仿真参数设置：主站信号与小站信号幅度比值h1/h2=4，不妨取h1=4，h2=1，数据长度L为1000，升余弦滤波器滚降系数α=0.35，Δθ仿真参数设置如表1所示。

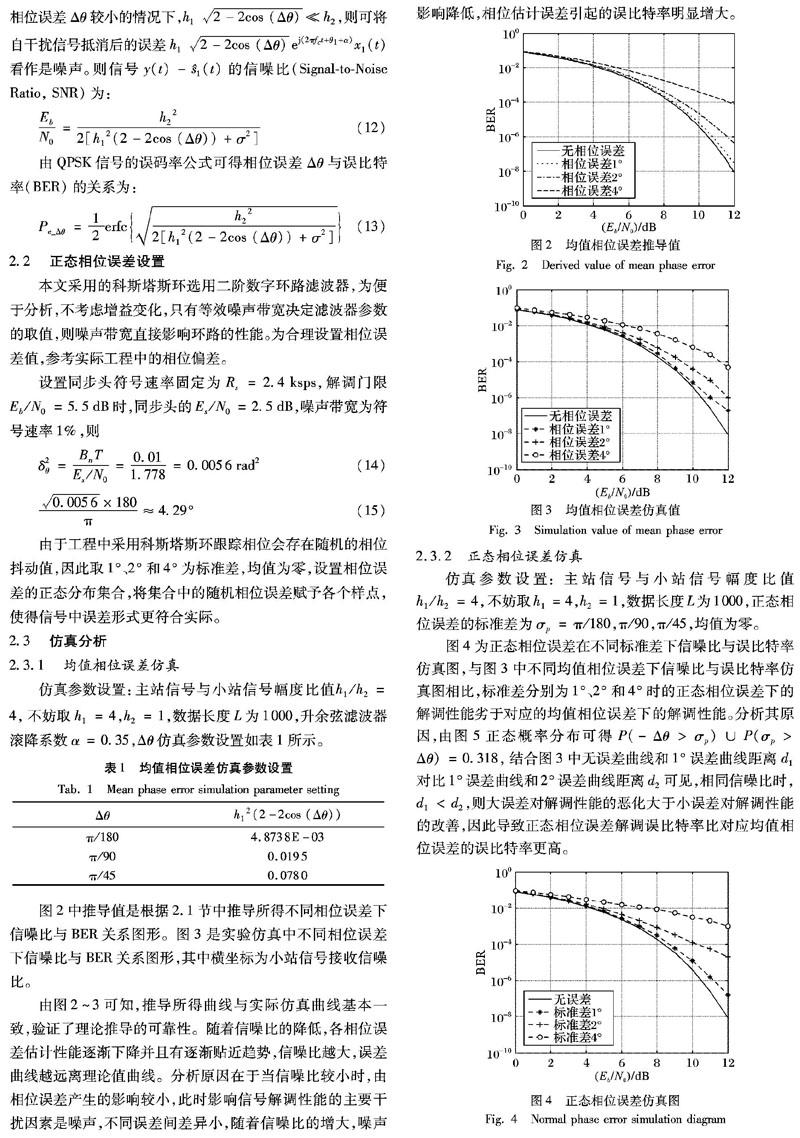
图2中推导值是根据2.1节中推导所得不同相位误差下信噪比与BER关系图形。图3是实验仿真中不同相位误差下信噪比与BER关系图形，其中横坐标为小站信号接收信噪比。

由图2～3可知，推导所得曲线与实际仿真曲线基本一致，验证了理论推导的可靠性。随着信噪比的降低，各相位误差估计性能逐渐下降并且有逐渐贴近趋势，信噪比越大，误差曲线越远离理论值曲线。分析原因在于当信噪比较小时，由相位误差产生的影响较小，此时影响信号解调性能的主要干扰因素是噪声，不同误差间差异小，随着信噪比的增大，噪声影响降低，相位估计误差引起的误比特率明显增大。

2.3.2 正态相位误差仿真

仿真参数设置：主站信号与小站信号幅度比值h1/h2=4，不妨取h1=4，h2=1，数据长度L为1000，正态相位误差的标准差为σp=π/180，π/90，π/45，均值为零。

图4为正态相位误差在不同标准差下信噪比与误比特率仿真图，与图3中不同均值相位误差下信噪比与误比特率仿真图相比，标准差分别为1°、2°和4°时的正态相位误差下的解调性能劣于对应的均值相位误差下的解调性能。分析其原因，由图5正态概率分布可得P（-Δθ>σp）∪P（σp>Δθ）=0.318，结合图3中无误差曲线和1°误差曲线距离d1对比1°误差曲线和2°误差曲线距离d2可见，相同信噪比时，d1

3 相位误差对幅度估计的影响

第2章对相位估计的正态误差进行了仿真与分析，并与均值相位误差的仿真进行了对比。由于信道参数估计是一个连续的过程，本章针对相位估计后产生的误差是否会对后续的幅度估计造成影响进行理论上的推导，再通过仿真验证推导的可靠性。

3.1 相位误差下的幅度估计算法

对于非对称PCMA信号来说，通常使用的对称PCMA信号和单信号的幅度估计算法都已经不再适用。由文献[9]通过多次实验得出的仿真结果可知，四次方法对非对称情况下主站信号的幅度估计较为准确，估计误差始终保持在一个较小值，且受幅度比的影响较小。因此，下面将重点研究四次方法并加以改进，以提高幅度估计算法精度。

四次方法是将接收信号中主站信号即自干扰信号的频率共轭抵消，得到辅助信号，本节考虑相位估计误差的存在，将辅助信号改成以下形式：

由式（23）易得：当σp=π/180，π/90，π/45，π/30时，h^1分别为0.9994h^p，0.9976h^p，0.9903h^p，0.9783h^p，其中设置σp=π/30用于对比。

3.2 仿真实验与结果分析

仿真参数设置如下：双路信号均采用QPSK调制，主站信号与小站信号幅度比值为h1/h2=4，不妨取h1=4，h2=1，噪声方差为σ2=0.09，符号序列长度为1000，正态相位误差的标准差为σp=π/180，π/90，π/45，π/30，均值為零。

图6为不同正态相位误差时幅度估计误差的仿真图。仿真序号表示实验序号，即第N次实验。当相位标准差σp=π/180，π/90时，存在正态相位误差时幅度估计误差曲线与无相位误差时幅度估计误差曲线基本一致;当σp=π/45，π/30时，两条曲线都存在较为明显的差异，由于区别较为显著，对这两个标准差作幅值曲线验证理论推导。

图7为σp=π/45，π/30时，存在正态相位误差时幅度估计值曲线与无相位误差时幅度估计值曲线。仿真序号表示实验序号，即第N次实验。由式（23）有h^1=e-2σp2h^p，则无相位误差时，h^1=h^p;相位标准差σp=π/45时，0.9903h^p;相位标准差σp=π/30时，0.9783h^p。从图7可见存在正态相位误差的曲线均低于无相位误差的曲线，且相位标准差为σp=π/30的曲线低于相位标准差为σp=π/45的曲线，通过在图7中取点作数值验证，其结果与理论推导所得结论相符，验证了推导的可靠性。

4 基于四次方法的搜索式幅度估计算法

前两章分别对相位估计正态误差以及正态误差对幅度估计算法的影响进行了分析，通过误差分析可知，在一定正態相位误差范围内，幅度估计算法受到相位误差影响较小，幅度估计误差在固定区间内波动。针对四次方法估计幅度值存在的不足，本章提出一种基于四次方法的幅度估计改进算法。研究主要思路是在四次方法的基础上，通过二阶和四阶矩（M2M4）算法对抵消后的信号信噪比进行估计，在误差波动范围内找到最大信噪比对应的最佳幅度估值，并与改进前的算法性能作出对比。

4.1 二阶和四阶矩估计法

针对抵消后信号的信噪比估计问题，本节采用二阶和四阶矩（M2M4）估计算法，该算法计算简便，易于实现，且具有无需恢复载波相位的特点，避免了相位误差对其影响。下面将通过简单的系统模型对该算法原理进行说明，基带等效系统模型如图8所示。

4.2 基于四次方法的搜索式幅度估计算法

针对幅度估计误差对信号解调影响较大的问题，为了提高系统的解调性能，在四次方法估计的基础上进一步修正幅度估值，提出相应的改进算法。

首先采用四次方法对接收信号进行幅度估计，得到粗略的幅度估值也就是中心值a，经过多次实验得到该估计算法的误差波动范围b，M2M4算法对自干扰抵消后的信号信噪比进行估计，该信噪比是存在自干扰信号残余的真实信号信噪比。由于自干扰信号抵消后的残余主要由幅度估计算法存在的估计误差引起，且该误差在一定范围内波动，通过在一定范围内的搜索，可得到信噪比的峰值，其对应的幅度为最佳的估计值。具体流程如下所示：

4.3 仿真分析

参数设置如下：双路信号均采用QPSK调制，主站信号与小站信号幅度比值h1/h2=4，噪声方差为M2，符号序列长度为1000。

图9为幅度最佳估计的搜索图。以四次方法估计所得幅度值为中心在误差波动范围内对抵消后信号的信噪比进行估计，搜索区间内最大信噪比估计值，最大信噪比对应的幅度值为最佳估计值。

图10为不同估计算法下误比特率曲线。通过对比用四次方法直接估计所得幅度值与最佳幅度估计值分别进行重构抵消后，小站信号的误比特率，得出在数量级为M4时，改进算法下小站信号的解调性能提升了1dB。

5 结语

针对实际应用中相位误差情况，提出了正态相位误差的概念。对正态相位误差进行了实验仿真并与均值相位误差对比，得出两者对解调性能影响存在差异的结论且作出合理分析，对提高PCMA信号解调性能具有理论指导意义。后针对幅度误差对解调性能影响较大的问题，为了进一步提升幅度估计算法的性能，提出了一种基于四次方法的幅度估计改进算法，通过搜索抵消后信号最大信噪比的方法，找到最佳的幅度估计值，实验结果表明改进算法对比原算法在误比特率为10-4时性能提升1dB，幅度估计算法精度的提升使自干扰信号的重构更接近真实值，利于后续的抵消分离。由于各参数的算法建立基本假设时，将卫星通信中信道参数视作是缓慢时变的，且为简化模型将其在一定时间段内视作是非时变的，采用的也是常规信道参数估计算法，然而实际上卫星信道因为高功放等往往会存在非线性变化，则信道参数有时变的特性，原有算法不再适用，造成参数估计的困难，并让分离解调无法正常实现，故还需对非线性条件下的研究作进一步的探索。

参考文献（References）

[1] DANKBERG M. Paired Carrier Multiple Access （PCMA） for Satellite Communications[C]// Proceedings of the 17th AIAA International Communications Satellite Systems Conference and Exhibit. Menlo Park， CA： AAAI Press， 1998： 787-791.

[2] DANKBERG M D， MILLER M G， MULLIGAN M G. Self-interference Cancellation for Two-party Relayed Communication： US5596439A[P]. 1997-01-21.

[3] 黄强. 单通道混合信号识别与APCMA信号盲分离技术研究[D]. 郑州：信息工程大学， 2017： 4-5. （HUANG Q. Research on single channel mixed signal identification and APCMA signal blind separation[D]. Zhengzhou： Information Engineering University， 2017： 4-5.）

[4] JANSSEN G J M. Receiver structrue for simultaneous reception of two BPSK modulated cochannel signals[J]. Electronic Letters， 1993， 29（12）： 1095-1097.

[5] 付迪， 高勇.非对称PCMA卫星信号的截获方法[J]. 现代电子技术， 2007（7）： 28-30， 34. （FU D， GAO Y. Signal interception method for asymmetric PCMA satellite communication systems[J]. Modern Electronics Technique， 2007（7）： 28-30， 34.）

[6] COOCH R P， SUBLETT B J. Demodulation of cochannel QAM signals [C]// Proceedings of the 1989 International Conference on Acoustics， Speech， and Signal Processing. Piscataway， NJ： IEEE， 1989： 1392-1395.

[7] ELTAIF T， SHALABY H M H， SHAARI S， et al. Performance analysis of a hybrid fiber Bragg grating-based spectral-amplitude-coding/successive interference cancellation for optical CDMA systems [J]. Optics Communications， 2009， 282（1）： 1-6.

[8] 徐星辰， 程剑， 唐璟宇.非对称PCMA信号解调性能分析[J]. 通信技术， 2018， 51（4）： 768-773. （XU X C， CHENG J， TANG J Y. Performance analysis of asymmetric PCMA signals demodulation[J]. Communications Technology， 2018， 51（4）： 768-773.）

[9] 郭一鸣. PCMA信号盲解调关键技术研究[D]. 郑州：信息工程大学， 2015： 18-20. （GUO Y M. Research on key technologies for blind demodulation of PCMA signals[D]. Zhengzhou： Information Engineering University， 2015： 18-20.）

[10] 张金成， 彭华， 赵国庆.信噪比估计算法研究[J]. 信息工程大学学报， 2011， 12（5）： 535-543. （ZHANG J C， PENG H， ZHAO G Q. Research on SNR estimation algorithms[J]. Journal of Information Engineering University， 2011， 12（5）： 535-543.）

[11] MAINI A K， AGRAWAL V. Satellite Technology： Principles and Applications[M]. New York： Wiley， 2014： 475-479.

[12] SONG B， LI J， CHEN P. Estimation algorithm of interference frequency offset in PCMA system[C]// Proceedings of the 2017 IEEE 2nd Advanced Information Technology， Electronic and Automation Control Conference. Piscataway， NJ： IEEE， 2017： 1094-1097.

[13] LEE J H. Self-interference cancelation using phase rotation in full-duplex wireless[J]. IEEE Transactions on Vehicular Technology， 2013， 62（9）： 4421-4429.

[14] ASKAR R， KAISER T， SCHUBERT B， et al. Active self-interference cancellation mechanism for full-duplex wireless transceivers[C]// Proceedings of the 9th International Conference on Cognitive Radio Oriented Wireless Networks and Communications. Piscataway， NJ： IEEE， 2014： 539-544.

[15] 楊勇. 成对载波多址信号的解调技术研究[D]. 郑州： 信息工程大学， 2013： 19-20. （YANG Y. Research on demodulation techniques of paired carrier multiple access signals[D]. Zhengzhou： Information Engineering University， 2013： 19-20.）

[16] 杨勇， 张冬玲， 彭华， 等. 单通道高阶调制线性混合信号的频偏估计[J]. 电子学报， 2015， 43（1）： 160-165. （YANG Y， ZHANG D L， PENG H， et al. Frequency offset estimation in single-channel linear mixture of high-order modulated signals[J]. Acta Electronica Sinica， 2015， 43（1）： 160-165.）

[17] 沈逸峰， 汪春梅. 试论成对载波多址系统中参数的联合估计[J]. 中国新技术新产品， 2013（4）： 6-7. （SHEN Y F， WANG C M. Test discussion on joint estimation of parameters in paired carrier multiple access system[J]. China New Technologies and Products， 2013（4）： 6-7.）

[18] 李天赐. 基于PCMA的盲解调技术研究[D]. 上海： 上海交通大学， 2014： 19-20. （LI T C. Research on blind demodulation of PCMA signals[D]. Shanghai： Shanghai Jiao Tong University， 2014： 19-20.）

[19] ADALI T， JUTTEN C， YEREDOR A， et al. Source separation and applications[J]. IEEE Signal Processing Magazine， 2014， 31（3）： 16-17.

[20] LU X Y， GAO B， KHOR L C， et al. Single-channel source separation using filterbank and 2D sparse matrix factorization[J]. Journal of Signal and Information Processing， 2013， 4（2）： 186-196.

[21] WU C L， LIU Z， WANG X， et al. Single-channel blind source separation of co-frequency over-lapped GMSK signals under constant-modulus constrains[J]. IEEE Communications Letters， 2016， 20（3）： 486-489.

[22] FRITSCHE C， KLEIN A， GUSTAFSSON F. Bayesian cramer-rao bound for mobile terminal tracking in mixed LOS/NLOS environments[J]. IEEE Wireless Communications Letters， 2013， 2（3）： 335-338.