多因子判定与渗流模型相结合的裂缝检测算法
2019-08-01安世全曹悦欣瞿中
安世全 曹悦欣 瞿中


摘 要:针对传统的基于渗流模型的裂缝检测算法效率过低且检测结果易存在断裂的问题,提出一种多因子判定与渗流模型相结合的裂缝检测算法。首先,提出了一种改进的渗流加速算法,通过减少大量参与渗流处理的冗余像素点,提高渗流处理效率;然后,对提取到的渗流点进行渗流处理;最后,提出了一种结合裂缝走向的多因子判定连接算法,算法通过四个判定因子对裂缝连接的合理性进行分析,以提高裂缝连接的准确性。对背景中存在不同干扰物的不同形态裂缝图像进行实验,与传统渗流模型检测算法以及原渗流加速骨架连接算法相比,所提算法中渗流点数量分别平均减少了99.7%与38.1%,精确率分别平均提高了60.5%与6.4%,召回率分别平均提高了10.5%与4.0%。实验结果表明,所提算法能够明显提高渗流处理效率,同时提高裂缝检测的准确性。
关键词:裂缝检测;渗流模型;多因子判定;裂缝连接
中图分类号: TP391.413
文献标志码:A
Abstract: Concerning the problem that traditional crack detection algorithm based on percolation model has low efficiency and detection results are prone to fracture, a crack detection algorithm based on multi-factor decision and percolation model was proposed. Firstly, an improved algorithm of accelerating crack inspection based on percolation model was proposed, which improves the efficiency of percolation processing by reducing a large number of redundant pixel points involved in percolation processing. Secondly, the extracted percolation points were used to percolation processing. Finally, a multi-factor decision connection algorithm based on crack orientation was proposed. In the algorithm, the rationality of crack connection was analyzed by four decision factors to improve the accuracy of crack connection. Different morphological crack images with different interfering objects in background were used in experiments. Compared with traditional percolation model detection algorithm and original algorithm of accelerating crack inspection based on percolation model and skeleton connection algorithm, the number of percolation points of the proposed algorithm was reduced by an average of 99.7% and 38.1%, respectively. The precision was increased by an average of 60.5% and 6.4%, respectively, and the recall was increased by an average of 10.5% and 4.0%, respectively. The experimental results show that the proposed algorithm can significantly improve the efficiency of percolation processing and improve the accuracy of crack detection.
Key words: crack detection; percolation model; multi-factor decision; crack connection
0 引言
由于車辆反复碾压,混凝土路面的结构层无法承受荷载,常导致路面损坏,产生裂缝。及时处理路面产生的病害,不仅可以保障行车安全,同时可以减少后期对公路养护的开支。传统的人工裂缝检测方式不仅耗时多、开支大,而且由于人工检测具有主观性,难以保障检测的准确性。相比之下,基于数字图像处理的裂缝检测具有高效性与客观性。
学者们提出了一系列基于数字图像处理的路面裂缝检测方法:Liu等[1]提出一种基于多尺度与视觉特征的裂缝检测算法,算法的鲁棒性较好,减小了低对比度对检测结果的影响,但裂缝细小部分可能被忽略。王军等[2]提出一种基于Hessian矩阵多尺度滤波的裂缝检测方法,该方法可有效实现裂缝特征的快速提取和分类,但易受路面背景污渍干扰。Aldea等[3]提出一种反向决策框架下的裂缝检测方法,该方法在图像模糊的情况下检测结果较好,但易忽略明显裂缝旁的细小裂缝。Sun等[4]提出一种用于路面裂缝检测的加权邻域像素分割方法,该方法鲁棒性强,可准确、快速地对裂缝图像进行分割,但检测结果受不均匀光照影响。任亮等[5]提出一种基于Prim最小生成树的裂缝连接算法,该算法在连接断裂的同时使用裂缝方向与对比度特征去除伪连接,但其连接结果仍存在很多断裂。赵珊珊等[6]提出一种基于卷积神经网络的裂缝检测方法,该方法对低对比度图像检测效果较好,但不适用于具有背景干扰物的图像。Amhaz等[7]提出一种基于最小路径的检测算法,该算法对裂缝细节信息保留较好,但计算量较大。宰柯楠等[8]提出一种基于遗传算法和简化脉冲耦合神经网络(Pulse Coupled Neural Network, PCNN)请补充PCNN的中文名称和英文全称的裂缝检测方法,该方法以最小误差准则作为遗传算法的适应度函数,实现了自适应阈值分割,但时间复杂度较高。朱平哲等[9]提出一种基于主动生长的断裂裂缝块的连接方法,该方法在提取裂缝边缘后对断裂部分进行连接,对细小断裂部分的连接效果较好,但效率一般。
目前的裂缝检测算法普遍存在易忽略裂缝细节部分的问题。Yamaguchi等[10-11]提出一种基于渗流模型的混凝土表面裂缝检测算法,该算法能够充分考虑裂缝的连通性与图像的局部细节,对细小裂缝识别率较高,但效率过低,裂缝易存在断裂。对此,Qu等[12]提出一种带有重叠窗口的裂缝预提取算法与基于骨架提取的连接算法,该算法在一定程度上提高了渗流处理效率,并改善裂缝断裂情况,但效率仍不理想。之后,瞿中等[13]提出一种渗流加速算法,改进了带有重叠窗口的预提取算法,极大提高了渗流处理速度,但检测精确率受到影响,检测效率仍有提高空间。
针对渗流处理冗余点过多导致的效率低、毛刺多等问题,本文提出一种改进的渗流加速裂缝检测算法,在保证检测精确率的同时,通过进一步减少渗流处理的冗余像素点,提高渗流处理效率,减少毛刺产生。为减少渗流处理结果中的裂缝断裂现象,保证裂缝完整性,根据裂缝连接时易产生的不合理连接现象,本文提出一种结合裂缝走向的多因子判定连接算法。
1 基于渗流模型的裂缝检测加速算法
渗流加速算法[13]中的暗点提取方法能够对裂缝进行粗提取,将基本不可能为裂缝的像素点排除,从而减少参与渗流处理的像素点个数。本文提出的改进渗流加速算法通过进一步处理提取到的暗点图,只保留必要的渗流像素点,提高渗流处理的检测效率。
1.1 暗点提取算法
暗点提取算法[13]的基本思想是:将图像划分为若干个带有重叠区域的窗口,根据每个小窗口的像素值均值与最小值之差所在的范围,设置小窗口内像素点的权值与提取比例;然后根据暗点提取比例选取窗口中灰度值升序排序靠前的像素点,排位越靠前权值越大;最后计算每个像素点的权值之和,根据全局提取比例提取权值靠前的像素点。
1.2 改进的渗流加速算法
渗流加速算法[13]中的暗点提取方法极大提升了渗流处理的速度,同时基本能够保持裂缝完整性,但渗流过程仍处理了大量冗余点。基于这点,本文提出了改进的渗流加速算法,对暗点图进行处理,保留暗点图中的孤立点以及提取到的裂缝骨架作为渗流点,从而减少非必要渗流点,进一步提高渗流处理的效率。为提高检测精确度,根据裂缝的走向提出了12邻域渗流方法,对骨架端点部分单独进行12邻域渗流。算法具体步骤如下:
1)对裂缝图像使用带有重叠窗口的暗点提取算法[13]进行处理,得到去噪后的暗点图。
2)运用8方向链码扫描与跟踪的图像细化算法[14]对暗点图进行细化,保留细化后的图像(包括短骨架)以及孤立点。
3)将暗点图中的孤立点,与提取到的骨架一起存入图operateImg中。
4)将图operateImg中的像素点依次作为渗流起始点Dp,在裂缝原图中进行渗流处理,得到渗流结果图resultImg1。
5)提取裂缝骨架的端点,将所有端点保存。
6)将提取的裂缝骨架端点依次作为渗流起始点Dp,然后对其12邻域进行渗流处理,得到渗流结果图resultImg2,12邻域示意图如图1所示。
7)将resultImg1与resultImg2进行合并,得到最终的渗流结果图resultImg。
本文提出的改进渗流加速算法只保留必要渗流点进行渗流,减少了渗流所需时间。在某些情况下,渗流检测结果可能会导致裂缝产生断裂,直接进行去噪会将较短裂缝同噪声一并去除,因此本文对检测结果不进行去噪。对图2(a)所示图像进行裂缝提取,图2(b)为原渗流加速算法的检测结果,本文算法结果如图2(c)所示。从实验结果可以看出,本文算法的检测结果并未因渗流点的减少而受到明显影响,由于对端点进行12邻域渗流,还可以检测到原算法未能检测到的部分,检测结果基本能保持原渗流加速算法的精确度。
2 结合裂缝走向的多因子判定连接算法
對于复杂裂缝的渗流结果,往往存在多处断裂,且断裂处形态各异,连接算法要尽可能准确连接断裂部分。文献[12]在连接裂缝时,没有考虑当前端点是否需要连接,并且连接范围有限,因此可能会造成误连接与漏连接。本文针对该问题,提出了结合裂缝走向的多因子判定连接算法。在判断连接点时,连接距离以及裂缝延伸方向尤为重要。其中,裂缝延伸方向应由整体方向及部分方向共同决定。裂缝整体走势只是裂缝的大致方向,并不能完全代表延伸方向,局部方向同样重要。本文中,分别使用裂缝弧度、方向因子考虑裂缝整体方向以及裂缝末端方向;然而如果仅根据连接长度与裂缝方向进行判断,通常会将距离与方向合适的线性噪声作为连接对象,由此产生误连接。通过考虑连接线的像素值,可以避免产生本不应存在的连接线,因此,本文算法通过计算连接长度、裂缝弧度、方向因子以及颜色比例,综合判定连接的合理性。
2.1 连接长度
当裂缝出现断裂时,两个裂缝区域往往距离较近。在指定搜索范围内,与裂缝末端的连接长度lenth越短的候选连接点,越有可能是合理连接点,因此,连接长度对裂缝的准确连接具有重要意义。lenth的示意图如图3所示,计算如式(1)所示:
其中:Epx与Dlx分别为端点与候选连接点的横坐标;Epy与Dly分别为端点与候选连接点的纵坐标。lenth取值过小会导致断裂无法连接,取值过大会降低连接效率,实验中取lenth≤25较为合理。
2.2 裂缝弧度
裂缝尾部的走向预示着裂缝的延伸方向。考虑到连接效率与噪声长度,选取裂缝骨架尾部5个像素点进行线性拟合,得到拟合直线角度α1;将当前裂缝端点与候选连接点连接,得到连接线角度α2。为使裂缝延伸方向遵循原裂缝走向,α1与α2的角度差α应控制在一定范围内,α的示意图如图3所示,计算如式(2)所示:
为遵循原裂缝走向,α应控制在较小范围内,实验表明α≤30°时搜索范围比较合理。当连接距离较近时,可能会出现较大连接角度,经过实验,lenth≤9时合理连接线的角度易于偏大,因此不限制α的取值范围。
2.3 方向因子
裂缝弧度考虑的是裂缝尾部的走向趋势,而方向因子[15]考虑的是裂缝末端方向,两者对于判断下一裂缝点的走向都起着重要作用。本文将方向因子作为连接线合理性的判断依据之一,根据方向因子来判断下一裂缝点在每个方向的可能性,与裂缝尾部方向共同控制裂缝延伸方向。将裂缝末端延伸方向定义为0~7八个方向,如图4(a)所示。
如果当前端点Ep的方向为0,则下一裂缝点在0方向上的可能性最大,距离0方向越远的方向可能性越小。当前端点方向为u时,八个方向i的方向因子Fi可根据式(3)~(4)计算:
其中:θui为u与i的夹角(如图4(a)所示), β为弧度权值(β=1.5)。图4(b)给出了u=0时,端点Ep的8邻域方向因子。
2.4 颜色比例
在判断连接是否误连时,连接线中的点在原图中的像素值是尤为重要的参考因素。连接线中较暗的像素点越多,则其越有可能是合理连接线。本文将连接线中像素值大于小于应为“ 小于”。
注:此处笔误,后续算法步骤中描述正确,故不影响后续实验及结论。平均值的点的个数占连接线总点数的比例,作为连接时的一个判定因子。根据连接线中的像素点位置,找到裂缝原图像中对应的像素点。连接线的平均像素值avgcolor的计算如式(5)所示:
其中:n为连接线的像素点总数;colori为像素点的像素值。根据式(6)计算连接线中colori><应为“ < ” 。avgcolor的像素点数量number在连接线中的比例proportion:
2.5 多因子判定连接算法
结合裂缝走向的多因子判定连接算法主要步骤如下:
1)去除渗流结果图中的点状噪声及孔洞,并对图像进行平滑处理。
2)运用8方向链码扫描与跟踪的图像细化算法[14],得到单一像素的骨架图。
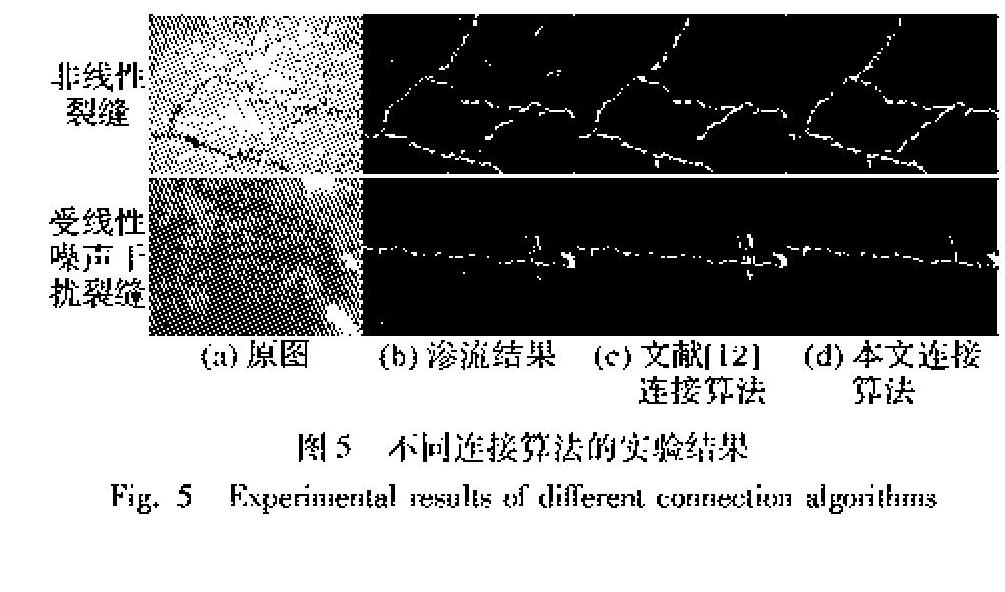
3)寻找骨架图中的连通区域,计算每个连通区域中像素点的个数Nl,将Nl 4)选取一个未处理的Ep,在该连通域的裂缝骨架上,取5个与当前Ep相邻的像素点进行线性拟合,得到拟合直线及其角度α1。 5)以Ep为中心,将步骤4)中拟合直线延伸方向两侧各30°,且半径为25的扇形区域,以及半径为9的圆形作为搜索范围,寻找与Ep属于不同连通区域的候选连接点Dl。 6)若在搜索区域未找到候选连接点,跳至步骤4)。 7)将Ep与Dl拟连接,得到连接线。 8)根据式(1)计算连接线的长度lenth。 9)计算连接线的角度α2,根据式(2)计算α1与α2的角度差α。 10)根据式(3)、(4)计算属于Ep的8邻域且属于连接线的像素点的方向因子Fi。 11)在原图中找到连接线对应的像素点。根据式(6)计算像素值colori小于连接线平均像素值avgcolor的像素点个数number在连接线中所占的比例proportion,其中avgcolor根据式(5)计算。 12)计算候选连接点的权值W,W的计算如式(7)所示: 13)从Dl中选出权值W最小的像素点Dmin,若W 当lenth≤9时,由于不限制α的取值范围,连接线方向与裂缝末端方向的夹角可能较大,方向因子取值较小,因此根据式(7)计算的权值偏大,故式(8)对TW分段取值。 14)若Dmin與之最近的骨架端点距离小于3,将端点设置为待连接点。 15)将Dmin与Ep分别在原图和骨架图上进行连接,更新骨架图的连通区域并检测新Ep,若还有未处理的Ep,跳至步骤4)。 16)对裂缝连接结果进行去噪。 某些情况下,渗流过程会使噪声演变为类似裂缝的细长形状,容易发生误连;同时,复杂裂缝的断裂往往很难准确连 接。图5为两组有代表性的渗流结果图的连接结果对比,可以看出,本文算法的连接准确性得到提高,连接结果更加合理。 3 实验结果及分析 实验采用了100幅400×300像素大小的混凝土路面裂缝图像进行测试,实验数据集由作者实验室拍摄采集,其中包括横向裂缝、纵向裂缝、网状裂缝等不同形状特征的裂缝,图像存在不同类型的噪声干扰因素,如光照、污渍、颜色不均的路面。实验软件和硬件环境:CPU为Intel Core i5-3210M 2.5GHz,OS为Windows 7,Library为OpenCV 2.3.0。本文选取了噪声与裂缝形态有代表性的4幅图像作为分析对象,实验结果如图6所示。 从图6的实验结果可以看出,三种算法对存在不同形态裂缝以及不同种类噪声的图像都能提取出较为完整的裂缝。图6(a)中,Image 5的背景颜色不均,但由于颜色不均区域为块状,因此并未对三种算法的实验结果造成干扰;Image 6的背景中存在细小线性污渍,对渗流结果容易造成一定干扰,但由于原渗流加速骨架连接算法以及本文算法对渗流结果进行连接,因此经过去噪可以将该噪声去除,而原渗流模型检测算法的检测结果存在很多断裂,强制去除噪声则会造成裂缝缺失,为保证裂缝完整性,受污渍影响的噪声无法去除;Image 7的背景粗糙不均,存在与裂缝颜色相似的点状颗粒,且裂缝周围有干扰物散落,但是对三种算法检测结果影响不大;Image 8中裂缝受到不均匀光照影响,该干扰因素对原渗流模型检测算法的影响较大,造成检测结果断裂,而另外两种算法由于对裂缝进行连接,检测结果并未受到明显影响。 实验结果表明,原渗流模型检测算法對复杂裂缝的细节信息提取更加完整,但更容易受到背景中干扰因素的影响,产生噪声、毛刺、断裂等;原渗流加速骨架连接算法对背景干扰因素不敏感,但断裂处存在误连接或漏连接的现象;本文算法同样对背景干扰因素不敏感,但连接更加准确、合理,检测结果更加接近真实裂缝。 为评估本文提出的算法性能,对原渗流模型检测算法、原渗流加速骨架连接算法以及本文提出算法的实验结果,运用精确率P与召回率R进行评估[10],如式(9)、(10)所示: 其中:Np是被正确检测的裂缝点数;Nr是人工提取的裂缝点数;Nt是检测结果中裂缝像素点数。 运用图2的Image 1~4和图6中的Image 5~8原图进行实验,精确率低表示误检的像素点多,召回率低则代表漏检的像素点多。从图7的精确率与召回率对比可以看出,原渗流加速骨架连接算法与本文算法的检测精确率与召回率基本都高于原渗流模型检测算法。虽然原渗流模型检测算法对Image 5的检测较为完整;但是由于毛刺过多,裂缝宽于真实裂缝,导致误检数量偏多,精确率较低。相比其他算法,本文算法减少了噪声的提取,检测较为准确,同时漏检现象得到改善,因此召回率和精确率相对提高。 表1为三种算法的加速效果分析。可以看出,两种改进的渗流加速算法相比原渗流模型检测算法都减少了大量渗流点;而本文提出的渗流加速算法在原渗流加速算法的基础上,进一步减少了参与渗流处理的像素点个数。 表2为3种算法的效率分析。经过分析,三种算法在渗流部分的时间复杂度均为O(n),其渗流处理时间完全由渗流点数决定。从表2可以看出,本文算法与原渗流加速骨架连接算法的处理时间相对较短。相对另外两种算法而言,本文算法由于减少了大量渗流点,渗流效率得到明显提升。在算法的连接部分中,原渗流加速骨架连接算法的时间复杂度为O(n);而本文算法由于分别对每个候选连接点进行4个因子的计算,相对于原渗流加速骨架连接算法来说,考虑因素更加全面,计算量增加,其算法时间复杂度为O(nm),因此连接时间相应延长,由此导致算法整体效率的提升幅度较渗流阶段而言有所减小。从表2可以看出,本文算法总效率仍存在小幅提升。 4 结语 针对渗流模型检测算法处理效率过低以及裂缝检测后连接过程中易产生漏连接与误连接的问题,本文改进了渗流加速算法,并提出了结合裂缝走向的多因子判定连接算法。本文提出的渗流加速算法大幅度减少了参与渗流处理的像素点个数,渗流处理效率得到明显提高,但细节信息有少量丢失;本文提出的连接算法提高了检测的精确率与召回率,但算法效率不理想。在接下来的工作中,如何提高连接算法的效率以及如何保留更多裂缝细节信息是下一步的研究重点。 参考文献 (References) [1] LIU X Z, AI Y F, SEBASTIAN S. Robust image-based crack detection in concrete structure using multi-scale enhancement and visual features [C]// Proceedings of the 2017 IEEE International Conference on Image Processing. Piscataway, NJ: IEEE, 2017: 2304 – 2308. [2] 王军,孙慧婷,姜志,等.基于Hessian矩阵多尺度滤波的路面裂缝图像检测方法[J].计算机应用,2016,36(S1):174-176.(WANG J, SUN H T, JIANG Z, et al. Pavement crack detection based on Hessian matrix multi-scale filtering [J]. Journal of Computer Applications, 2016, 36(S1): 174-176.) [3] ALDEA E, LE HGARAT-MASCLE S. Robust crack detection for unmanned aerial vehicles inspection in an a-contrario decision framework [J]. Journal of Electronic Imaging, 2015, 24(6): 061119. [4] SUN L, KAMALIARDAKANI M, ZHANG Y M. Weighted neighborhood pixels segmentation method for automated detection of cracks on pavement surface images [J]. Journal of Computing in Civil Engineering, 2016, 30(2): 04015021. [5] 任亮,徐志刚,赵祥模,等.基于Prim最小生成树的路面裂缝连接算法[J].计算机工程,2015,41(1):31-36.(REN L, XU Z G, ZHAO X M, et al. Pavement crack connection algorithm based on Prim minimum spanning tree [J]. Computer Engineering, 2015, 41(1): 31-36.) [6] 赵珊珊,何宁.基于卷积神经网络的路面裂缝检测[J].传感器与微系统,2017,36(11):135-138.(ZHAO S S, HE N. Pavement crack detection based on convolution neural network [J]. Transducer and Microsystem Technologies, 2017, 36(11): 135-138.) [7] AMHAZ R, CHAMBON S, IDIER J, et al. Automatic crack detection on two-dimensional pavement images: an algorithm based on minimal path selection [J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(10): 2718-2729. [8] 宰柯楠,徐江峰.基于遺传算法和简化PCNN的裂缝检测方法[J].计算机应用研究,2017,34(6):1885-1888.(ZAI K N, XU J F. Method of crack detection based on genetic algorithm and simplified pulse coupled neural network [J]. Application Research of Computers, 2017, 34(6): 1885-1888.) [9] 朱平哲,黎蔚.基于主动生长的断裂裂缝块的连接方法[J].计算机应用,2011,31(12):3382-3384.(ZHU P Z, LI W. Linking algorithm of discontinuity crack block based on autonomous edge growing [J]. Journal of Computer Applications, 2011, 31(12): 3382-3384.) [10] YAMAGUCHI T, HASHIMOTO S. Automated crack detection for concrete surface image using percolation model and edge information [C]// Proceedings of the 2006 IEEE Conference on Industrial Electronics. Piscataway, NJ: IEEE, 2006: 3355-3360. [11] YAMAGUCHI T, HASHIMOTO S. Fast crack detection method for large-size concrete surface images using percolation-based image processing [J]. Machine Vision and Applications, 2010, 21(5): 797-809. [12] QU Z, GUO Y, JU F R, et al. The algorithm of accelerated cracks detection and extracting skeleton by direction chain code in concrete surface image [J]. The Imaging Science Journal, 2016, 64(3): 119-130. [13] 瞿中,郭阳,鞠芳蓉.一种基于改进渗流模型的混凝土表面裂缝快速检测算法[J].计算机科学,2017,44(1):300-302.(QU Z, GUO Y, JU F R. Algorithm of accelerated cracks detection based on improved percolation model in concrete surface image [J]. Computer Science, 2017, 44(1): 300-302.) [14] 瞿中,蒋玉萍,文倩云.一种方向链码扫描与跟踪的图像细化后期处理算法[J].计算机科学,2015,42(2):292-295.(QU Z, JIANG Y P, WEN Q Y. Algorithm of image thinning post-processing based on direction chain code scanning and tracking [J]. Computer Science, 2015, 42(2): 292-295.) [15] 吴成东,卢佰华,陈东岳,等.基于方向特征及引力模型的路面裂缝检测[J].东北大学学报(自然科学版),2012,33(4):469-472.(WU C D, LU B H, CHEN D Y, et al. Pavement crack detection based on direction feature and gravitational model [J]. Journal of Northeastern University (Natural Science), 2012, 33(4): 469-472.)
