共享交通的时空轨迹检索与群体发现
2019-08-01段宗涛龚学辉唐蕾陈柘
段宗涛 龚学辉 唐蕾 陈柘

摘 要:为解决共享交通下的共乘用户群体发现效率低、准确率不高问题,依据R-树原理建立GeoOD-Tree索引,并在此基础上提出以最大化共乘率为目标的群体发现策略。首先,对原始时空轨迹数据进行特征提取与标定处理,挖掘有效出行起讫点(OD)轨迹;其次,针对用户起讫点轨迹的特征,建立GeoOD-Tree索引进行有效的存储管理;最后,给出以最大化共乘行程为目标的群体发现模型,并运用K最近邻(KNN)查询对搜索空间剪枝压缩,提高群体发现效率。采用西安市近12000辆出租车营运轨迹数据,选取动态时间规整(DTW)等典型算法与所提算法在查询效率与准确率上进行性能对比分析。与DTW算法相比,所提算法的准确率提高了10.12%,查询效率提高了20约15倍。实验结果表明提出的群体发现策略能有效提高共乘用户群体发现的准确率和效率,可有效提升共乘出行方式的出行率。
关键词:共乘出行;群体发现;时空轨迹;3维R树;起讫点
中图分类号: TP301.6
文献标志码:A
Abstract: Concerning low efficiency and accuracy of the ridesharing user group discovery in shared transportation environment, a GeoOD-Tree index was established based on R-tree principle, and a group discovery strategy to maximize the multiplying rate was proposed. Firstly, the feature extraction and calibration processing of original spatio-temporal trajectory data was carried out to mine effective Origin-Destination (OD) trajectory. Secondly, a data structure termed GeoOD-Tree was established for effective storage management of OD trajectory. Finally, a group discovery model aiming at maximizing ridesharing travel was proposed, and a pruning strategy using by K Nearest Neighbors (KNN) query was introduced to improve the efficiency of group discovery. The proposed method was evaluated with extensive experiments on a real dataset of 12000 taxis in Xian, in comparison experiments with Dynamic Time Warping (DTW) algorithm, the accuracy and efficiency of the proposed algorithm was increased by 10.12% and 1500%此处英文的描述,与中文描述的20倍不一致? respectively. The experimental results show that the proposed group discovery strategy can effectively improve the accuracy and efficiency of ridesharing user group discovery, and it can effectively improve the rideshared travel rate.
Key words: ridesharing; group discovery; spatial-temporal trajectory; 3-Dimensional R-tree (3DR-tree); Origin-Destination (OD)
0 引言
作为一类新兴交通出行方式,共享交通的出现有助于缓解交通拥堵与道路磨损,减少空气污染,降低对能源的依赖性[1]。通过充分利用交通运输资源来提供多种形式和廉价方便的共享服务,改变人们传统的消费观念,变拥有汽车为使用服务。由于人类的社会群居特性,人们通常期望能够与具有相同出行特征的用户结伴出行[2],例如通勤共乘者往往具有相同的出行活动路径[3]。正是这种优于陌生乘客的潜在特征关联,使得乘客们在享受低廉优惠的共享交通出行时,也能够快速达成一致决策(如是否调整出行时间,是否绕道接载),提升用户体验,从而促进人们选择共享交通出行并加以保持,因此,充分考虑个体用户的活动信息,推荐与其具有相似出行活动的用户,形成不同共乘群体,有助于保证高效与经济的共享出行,同时从群体层面上引导调控交通需求,优化资源配置[4]。
共乘群体是指同一时间使用同一车辆出行的一组用户[5]。他们有着相似的出行活动,即相近的出发时间、出发地点以及目的地。共乘群体发现是查询个体乘客在出行活動上的相关性,为其推荐合适的群体进行共乘。共乘群体发现离不开轨迹数据的支撑。近年来,随着移动传感设备以及视频捕捉设备的广泛应用,轨迹数据获取变得越来越便捷,能够很好地表达用户出行活动的时空特征;然而高采样率产生了海量携带时间标签的全球定位系统(Global Positioning System, GPS)数据,造成了群体发现中由于频繁聚簇与簇内外查询带来的高计算成本[6],因此,构造高效的数据结构来管理大规模的轨迹数据,挖掘具有相似出行活动的用户形成共乘群体,将显著提高用户的共享出行体验。
国内外专家学者对共乘群体发现问题展开了不同的分析研究。这些研究更多的是规划用户的出行活动计划,包括匹配司乘双方[7-8]、选择见面地点[9-10]及优化路径[11]。这些工作多是对数据的直接处理,没有考虑大规模轨迹数据的处理。目前较少工作开展建立共乘出行的轨迹索引结构及群体快速查询研究,因此有必要从轨迹检索的角度深入解决共乘群体发现问题。
本文分析了共乘出行下的时空轨迹及群体特征,提出了以共乘率为优化目标的群体发现模型描述。扩展三维R树(3DR-tree)构造可高效管理起讫点(Origin-Destination, OD)轨迹的GeoOD(Geographic OD)-Tree索引结构,提供过滤机制,降低检索空间,提高群体发现效率。本文所做的主要工作如下:
1)定义共乘出行下群体发现问题,提出运用3DR-tree索引结构来查询在时空域下具有相似出行活动的用户。
2)设计GeoOD-Tree索引结构,用于存储并压缩海量OD轨迹,提出基于该结构的共乘群体发现方法。采用真实大数据验证所提方法的可行性。
MixQuery,为使得MixQuery不突兀,在原文(引言最后一段):2)设计GeoOD-Tree索引结构,用于存储并压缩海量OD轨迹,提出基于该结构的共乘群体发现方法。采用真实大数据验证所提方法的可行性。添加一段描述:现为:2)设计GeoOD-Tree索引结构,用于存储并压缩海量OD轨迹,提出基于该结构的共乘群体发现方法,即混和时间域和空间域同时进行相似群体查询(Mix Spatio-temporal Query),简称MixQuery。采用真实大数据验证所提方法的可行性。
2)设计GeoOD-Tree索引结构,用于存储并压缩海量OD轨迹,提出基于该结构的共乘群体发现方法,即混合时间域和空间域同时进行相似群体查询(Mix spatio-temporal Query, MixQuery),采用真实大数据验证所提方法的可行性。
1 相关工作
1.1 共乘群体发现
共乘群体推荐问题,主要通过分析不同用户的出行活动信息,匹配具有相似出行活动的用户并将他们作为一个共乘群体。国外诸多专家学者针对共乘群体推荐问题展开了不同的研究。Ghoseiri等[12]进行了共乘匹配研究并提出了最优匹配模型,通过分析接收到的不同乘客以及司机的出行活动计划,将时间和空间上邻近的乘客群体与司机进行匹配,从而得到共乘群体。Vanoutrive等[13]基于用户的历史移动行为建立变阶马尔可夫模型(Variable Order Markov Model, VOMM),将出发地点、出发时间与目的地相同的用户作为一个潜在共乘群体。Bakkal等[14]提出了一个新颖的共乘群体推荐方法,通过对出行轨迹数据建立Neo4j时空树模型,过滤出行时间和地点信息,将出行时间和地点匹配的用户作为最终的共乘群体。
1.2 时空轨迹索引
时空索引技术主要是针对海量时空数据的无序性,通过对海量时空轨迹建立时空索引,可以提高轨迹查询的效率。时空轨迹索引方法一般可以被分为三类:1)索引历史轨迹;2)索引当前位置;3)索引移动对象的未来位置。由于R-tree[15]在空间数据库的良好表现,当前研究的空间轨迹的索引结构多是基于R-tree展开的。第一种是针对大规模历史轨迹的索引方法,如历史R+树(Historical R+-tree, HR+-tree)[16]、多版本三维R树(Multi-Version 3DR-trees, MV3R-tree)[17]等。HR+-tree是一类重叠和多版本结构的R-树,它将时间维孤立于空间维,然后在每个时间片上建立一个R树,在进行时间片查询时退化为R-树的空间查询。第二种索引方法主要是针对需要回答与当前时间相关的查询,如基于更新标签的R树(R-tree with Update Memo RUM-tree)[18]、延迟更新的网格索引(Lazy-Update Grid-based, LUGrid)[19],其中RUM-tree基于备忘录的方式进行更新,将更新操作的成本降低到只有插入操作的成本。第三种索引方法则是为了预测移动对象的未来位置设计的索引结构,如时间参数化R树(Time Parameterized R-tree, TPR-tree)[20]、时间参数化的R*树(Time Parameterized R*-tree, TPR-tree)[21],其中TPR-tree实际上是以时间为参数的R*-tree,索引结构的节点中存储了对象位置和该位置上的速度,可以支持查询未来时刻的轨迹信息。
1.3 时空轨迹相似性
时空轨迹相似性的计算不同于空间轨迹相似性,它要求某种形式上的采样点对齐,即通过时间的順序来映射点以计算轨迹相似性;同时,它允许轨迹时移,因此两个轨迹的采样时间戳不必严格一致。研究人员对时空轨迹的相似性作了广泛的研究。Assent等[22]利用动态时间规划(Dynamic Time Warping, DTW)的方法,它允许一些点可以重复计算以进行最佳对齐,但噪声的存在使得重复计算会带来无意义的误差。Vlachos等[23]利用最长公共子序列(Longest Common SubSequence, LCSS)方法消除噪声,但是未解决处理时间轴拉伸和收缩带来的变形问题此处不通顺,应该是“未解决”吧?。Chen等[24]通过剔除实际补偿编辑距离(Edit distance with Real Penalty, ERP),利用阈值ε来量化匹配;作为一种改进,将ERP与DTW方法的优势结合,通过使用恒定的参考点计算距离来处理时间偏移。Frentzos等[25]提出了相异性度量(DISSIMilarity measure, DISSIM)算法,通过两个轨迹之间的欧氏距离的时间函数的定积分,定义了两个轨迹的不相似性,算法要求这两个轨迹具有相似的采样周期(即每个采样时间戳在两个轨迹中都存在采样点);但是,由于仅考虑一对一映射,DISSIM无法应对本地时间偏移,因此,只有当它们以相同的速度行进时,DISSIM才能在非均匀采样率下检测轨迹之间的相似性。Sankararaman等[26]提出对DTW的一种改进算法——模型驱动算法(Model-driven Assignment, MA),它在轨迹点对齐方面更加灵活。相似的轨迹部分比不相似的部分(间隙部分)贡献更高的MA分值;但是它引入了时间倒退的对齐,因此违反了时间序列匹配的基本前提。
2 共乘出行下的群体发现
在这一章中提出了共乘群体及其共乘路径,进而采用共乘率形式化描述群体发现问题。在计算共乘率时,本文假设乘客接受为其推荐的共乘群体。
2.1 基本定义
其中:
定义4 群体。给定乘客OD轨迹Qi,若存在M个乘客的OD轨迹Qm,使得m∈[1,M](QiQm),则可形成具有相似出行偏好的群体RGi根据T为转置,那么RGi应该是矢量、向量或矩阵吧?若是的话,全文的RGi是否均是矢量、向量或矩阵?请明确。否则无法理解。要注意修改的连贯性=(kim)1×MT·UM此处的T,是何意?与前面一样,是集合?还是表示向量的转置?请明确。若为向量、矢量或矩阵的转置,请将文中的向量、矢量或矩阵标识出来(这些需特别加黑处理),我们按照你的提示再修改:
0,其他
2.2 问题描述
为提高共乘效率,降低司乘双方共乘成本,有必要准确推荐群体,使得成员选取的共乘路径最长。给定一组群体RGi的OD轨迹QiRG=(Q1,Q2,…,Qs,…,QH)i,与司机OD轨迹Qdrive,一组协商上下车地点up、off,群体发现问题是搜寻一组乘客形成群体,使得其成员共乘率最大。
定理1 当群体成员具有相似的OD轨迹时,其群体共乘率最大。
证明 根据定义6,通过减少乘客的步行成本,能够提高共乘率。当给定一组群体RGi,当两成员满足min(dist(oi,os)+dist(di,ds))。条件使QiQs时,成员到达其约定地点距离总和最近,换乘空间成本最低,因此,通过将具有相似OD轨迹的乘客推荐为一个群体能够保证共乘成本最小,从而使得共乘率最大。
其中:‖·‖∞上面的公式中没有出现“‖‖”符号,是哪个公式写漏了?=max1≤i,s≤M(·);Dists(·)为两点的时空距离,dist(·)为两点的空间距离何意,需补充其所代表含义。
共乘用户群体发现是针对出行用户群里的应用目标。选择群体以用户出行的空间和时间两个特征作为选择标准,挖掘具有特定时间范围和空间范围的出行者共乘小组。群体发现算法具有一般的过程:首先定义群体的特征,然后建立描述群体聚集度的函数表达,最后设计算法对定义的群体进行发现。通常群体发现是NP难问题,因此需要设计启发式算法求其最优解[27]。本文采用基于个体属性特征的群体发现算法,利用R树的聚类特性,通过个体属性向量之间的相似性作为基础,在属性空间中划分群体。在第3章中引入基于R树的索引结构,并仔细说明如何进行基于GeoOD-Tree的群体发现策略。
3 基于3DR-tree的群体发现策略
3.1 轨迹标定
时空轨迹体现了用户在不同地点的停留与转移活动,能够挖掘用户的出行特征,包括出行时间、出行OD与出行方式等。相关工作采用GPS数据来识别用户出行活动[28],然而GPS数据在一定程度上隐藏了大量语义信息,而且,按照不同采样速率与策略(例如基于持续时间、区域范围等)识别的轨迹可能会出现不一致[29],这将导致后期对相似用户与群体发现的错误识别。
在OD轨迹中,一个停留地点可以看作是一次行程的出发地或目的地。停留地点描述了用户发生停留活动的地理区域。一个停留地点具有确定的时空信息,包括地理空间(lat,lon)与停留时段(arvtime,levtime),因此,可采用停留地点来标定OD轨迹。
本文的前期工作[30]中,采用有限驻留点(Limited to Stay Point, LSP)聚类算法提取原始轨迹的驻留点。LSP算法是通过在给定的时空域内分析停留活动,搜寻由GPS数据缺失与波动影响的一组位置信息。这样,采用一组停留地点可挖掘用户的出行OD信息,进而形成一条OD轨迹。
3.2 GeoOD-Tree索引结构
为有效管理用户的OD轨迹,提供对sODsOD为何意?请补充说明轨迹的快速检索,本文引入了3DR-tree索引结构[31]。3DR-tree是在R-tree的基础上加入时间域,扩展成3维R-tree。该结构从叶子节点开始,运用最小边界立方体(Minimum Bounding Box, MBB)覆盖全部对象。通过自下而上地增加树节点,增加MBB面积,实现对空间数据进行分割。
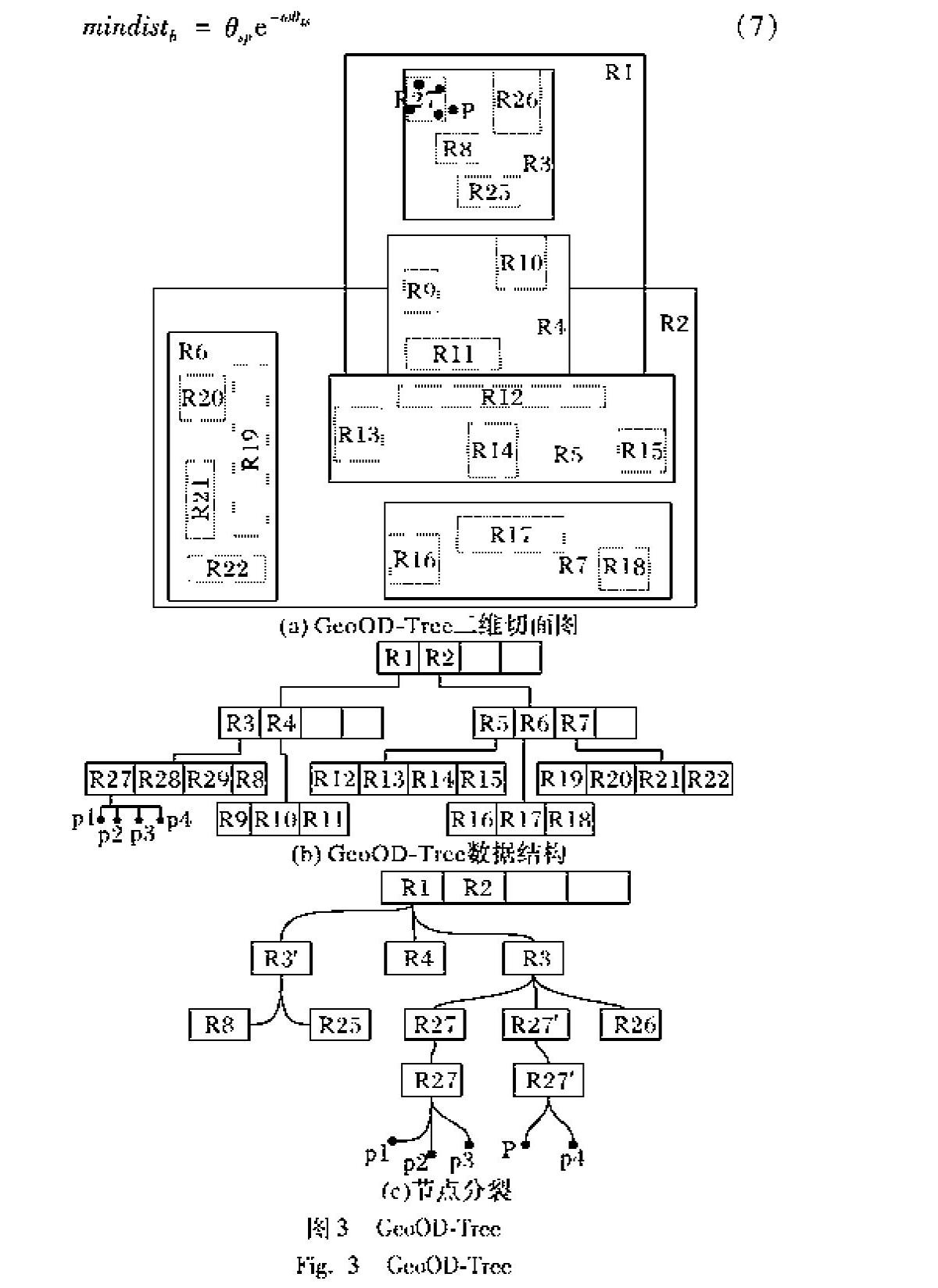
本文扩展3DR-tree来构建OD轨迹的索引结构,GeoOD-Tree(Geographic OD-Tree)。图2展示了GeoOD-Tree的索引結构实例。假定节点的最大条目数M=4,图2(a)给出中间节点(R1、R2)和叶子节点(A、B、C、D、E)结构。每个叶子节点分别存储一组邻近的停留地点及其对应的用户信息。其中,采用(ID,state)二元组来描述用户信息,分别代表用户ID和地点的类型标记,该标记用于表明该地点是出发地或目的地。GeoOD-Tree采用MBB覆盖上述对象的边界,如图2(b)中节点D所示。节点R1、R2存储了MBB标识和指向子节点的指针,采用(I,child-pointer)二元组表示,如图2(b)中,R1的MBB包含了A、E、F的MBB。
在GeoOD-Tree中,除了根节点,每个节点至少包含m且至多包含M个条目(1 与传统R-Tree相似,GeoOD-Tree索引结构能够在叶子节点中插入出发地或目的地对象。图3(a)为实例的二维空间切面图。当需要进行插入操作(图中所示的对象P)时,比较对象插入前后各叶子节点MBB体积的变化,选取变化最小的叶子节点作为插入目标。在图3(b)中,从根节点R1、R2开始,若P插入到R1时该节点对应的MBB体积变化最小,则选取R1作为候选插入目标进行深度搜索。在同一层进行广度搜索,确定R3与R27节点为不同层的候选插入目标。分裂步骤如图3(c)所示,由于受节点条目容量(M=4)影响,若P插入到R27时该节点发生上溢,则启动平方分裂操作。R27分裂成两个节点:R27和R27′,调整GeoOD-Tree结构形成平衡树,保证后期查询效率的稳定性。 当将R27′插入到节点R3时候,继续受节点条目容量的影响,R3发生上溢,继续启动平方分裂操作,R3分裂成R3和R3′。根据体积最小原则,R3存储R27、R27′、R26,R3′存储R8、R25。由于R3所在节点的条目数小于M,R1节点不再分裂。 3.3 节点剪枝 群体发现在于查询一组具有相似OD轨迹的乘客。传统的查询方法需要对所有OD对进行相似性评估与排序,通常需要获取轨迹的全局特征信息,导致高计算成本,为此降低搜索空间、减少不必要计算是提高群体发现效率的必要措施。 本文將乘客的换乘空间成本作为影响共乘出行选择的因素。当换乘空间成本超过θsp或等待时长超过θts时,用户将放弃共乘出行,群体发现无效。本文采用基于mindist[32]的剪枝方法预先过滤存储此类用户OD的子树来减少节点访问次数。本文首先确定查询阈值mindisth,用于向上剪枝无法共乘的节点。 其中,mindisth阈值的确定公式为: 在传统空间数据库中,OD轨迹的数据量巨大且数据结构复杂,通常OD轨迹涵盖了时间和空间两个属性,在进行K最近邻(K Nearest Neighbors, KNN)查询时,通常需要进行两步查询,首先进行时间或空间查询,然后再进行空间或时间查询,使得最后查询的时间和空间代价非常昂贵。GeoOD-Tree中的每个节点包含了时间和空间信息,利用提出的时空距离计算公式可以同时进行时间和空间的查询,因此使得查询代价降低。同传统R树一样,KNN查询和范围查询是由根节点开始向下查询,直到叶子节点。查询过程中需要遍历每个节点的子节点的最小外包矩形与待查询对象的距离,然后选取合适节点继续向下一层遍历。在进行遍历过程中加入上文所提剪枝算法,如果在一次计算中,节点距查询对象的距离大于mindisth,则可以直接减掉该节点,从而可以大幅度减少查询过程中的计算量,提高GeoOD-Tree的查询效率。 3.4 群体发现策略 本文在时空约束下压缩搜索空间,提供了基于KNN的OD轨迹查询。OD轨迹查询的描述如下。 本文在时空约束下压缩搜索空间,基于KNN方法,对OD轨迹进行时空阈混合查询即MixQuery。OD轨迹的混合查询的描述如下。 本文从GeoOD-Tree根节点进行最佳优先搜索。用KNN查询分别搜索满足上述条件的K个对象。以下给出了此类查询的执行过程,最终将查询得到两个集合OSet,DSet。通过对两个集合在用户ID上取交,返回候选OD对集合法返回候选OD对集合,算法如下此句不通顺,请作相应调整。 4 实验结果与分析 4.1 数据描述 本文使用西安市一天的出租车营运数据(全市有12000余辆出租车,一天的原始轨迹的数据辆约2.8GB)。经过数据预处理和轨迹标定后,提取约1205700条出租车OD轨迹数据。 4.2 参数设置 本文设定了GeoOD-Tree中最小条目数m与最大条目数M关系为m=M/2。本文首先分析了M对构造GeoOD-Tree的影响,如图4(a),当M<32时,随着M的增大,建立完整的GeoOD-Tree结构所花费的时间呈缓慢下降趋势。在M=32时,建立的花费时间达到最低,但随着M的继续增大,GeoOD-Tree花费时间呈快速上升趋势。对于M参数与树的深度关系,如图4(b)中,随着M的增大,与之对应的树的深度随之下降。 为了探究参数M对查询速度的影响,本文对比了KNN查询和Range查询效率与M值的关系。实验设置K为500,结果如图5(a)所示,KNN的查询效率曲线近似V字型,在M为32时,KNN查询时延最小。 然后实验继续分析了Range查询效率,本文在数据集范围内随机生成1000个Range查询,可以看到在M为32时查询效率最高。随着M的增大效率降低,在M为128时发生波动,查询效率达到最低,然后随着M的增大效率开始缓慢上升,但始终低于M=32时的查询效率。 上述实验中,在M=32时,建立GeoOD-Tree的时间达到最小,当M继续增大时,建立时间随之增大,这是因为在建立GeoOD-Tree的过程时,由于每个节点索引条目较多,在调整树形以保证所有节点都在同一深度时,需要花费更多的时间。在进行查询时,当树的深度增加时,需要进行多次计算来查找与查询对象相交的节点。由于节点的MBB会出现重叠,因此当M增大时,节点之间的重叠度增加,在进行查询时可能会遍历较多无关节点降低了整体查询效率。通过图5可以看到,当M=32时,范围查询和KNN查询都达到了最高效率,因此,本文选取M=32作为后续OD查询的参数。 4.3 查询性能分析 本文选取DTW以及Duan等[30]算法进行对比,DTW算法是处理时空轨迹的经典算法,当前的大多数的时空轨迹的查询都是在DTW的方法上进行改进。Duan等[30]算法是前期工作利用停留点建立用户位置轨迹和服务轨迹模型来进行相似用户发现的算法。 关于ByPOI:ByPOI是对论文Duan等[30]论文所用算法的一个总结,并没有给定全称,故根据其特征用ByPOI来代替此方法。 为便于理解,在本文的原文:本文选取DTW以及Duan中的算法,DTW算法是处理时空轨迹的经典算法,当前的大多数的时空轨迹的查询都是在DTW的方法上进行改进。Duan 算法是前期工作利用停留点建立用户位置轨迹和服务轨迹模型来进行相似用户发现的算法。添加部分描述。 现修改为:本文选取DTW以及Duan [30]中提取的算法ByPOI,DTW算法是处理时空轨迹的经典算法,当前的大多数的时空轨迹的查询都是在DTW的方法上进行改进。ByPOI算法是前期工作利用停留点建立用户位置轨迹以及利用POI建立服务轨迹模型来进行相似用户发现的算法。 本文选取DTW以及Duan等[30]提出的算法ByPOI,DTW算法是处理时空轨迹的经典算法,当前大多数的时空轨迹的查询都是在DTW方法上进行改进。ByPOI算法是前期工作利用停留点建立用户位置轨迹以及利用POI(Point of Interest)建立服务轨迹模型来进行相似用户发现的算法。 在实验中,将时间变化范围设置为5min,对应空间距离设置为[300,400,500]。进行归一化后设定λ∈[0.0177,0.0197],τ∈[0.0035],δ=λe-ωτ∈[0.0175,0.0195],其中ω=-2。圖6给出了算法的性能对比。在查准率方面图6(a):在δ等于0.0185时,即空间约束为500m、时间约束为5min时,本文提出的算法的准确率达到最高为79%;随着δ的增加,对共乘的约束减小,即空间和时间的范围更大,在实际共乘交通中这将导致出行用户放弃共乘,因此导致了查准率的下降。在查全率方面图6(b):随着δ的增加,即意味着空间和时间的约束变得宽松,所有算法的查全率都有所提高,并且提出算法的查全率都比其他算法高;在δ=0.0185时,本文所提算法的准确性达到最高为86%。为了评价算法的综合的性能,比较了三种算法的F1值此处是否应该为“F1”?请明确。回复:文中应为F1值,结果如图6(c)所示,三种算法在δ=0.0185时达到最好,接着随着δ的增大准确度开始下降;在具体表现方面,本文所提的算法比其他两种算法平均高出约9%。最后,本文比较了三种算法的执行效率,如图6(d),本文算法由于采用了GeoOD-Tree,在进行群体查询时的时间花费上其他两种算法几倍的几分之一,效率远远高于其他两种算法。通过四个实验对比,可以看出本文提出的MixQuery算法在查准率和查全率方面皆优于其他两种算法,而在加入了GeoOD-Tree索引后,算法整体效率远远高于其他两种算法,因此,本文提出的群体发现算法明优于其他两种算法。 5 结语 本文运用时空轨迹分析共乘出行特征与群体发现问题,首先定义了以最大共乘率为目标的群体发现模型,将问题转化为搜索一组具有相似OD轨迹的乘客;然后设计了GeoOD-Tree索引结构来有效存储与管理出行OD轨迹,并设计有效的剪枝算法以进行快速查询满足时空约束的用户组成群体;最后通过真实出租车营运数据对提出的算法进行性能评估。实验结果表明,本文提出的算法比其他算法具有较高的查询效率以及较优的查全率与查准率。在未来的工作中,将继续分析并存储出行路径、活动类型等特征,进一步提高群体发现方法的适用性。 参考文献 (References) [1] ZHANG D, HE T, LIU Y, et al. A carpooling recommendation system for taxicab services [J]. IEEE Transactions on Emerging Topics in Computing, 2017, 2(3):254-266. [2] ARTAN Y, BULAN O, LOCE R P, et al. Passenger compartment violation detection in HOV/HOT lanes [J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(2):395-405. [3] DONG H, MA L, BROACH J. Promoting sustainable travel modes for commute tours: a comparison of the effects of home and work locations and employer-provided incentives [J]. International Journal of Sustainable Transportation, 2016, 10(6): 485-494. [4] 陈艳艳,刘小明.城市交通出行行为机理及引导策略[M].北京:科学出版社,2016:10-13(CHEN Y Y, LIU X M. Urban Traffic Travel Behavior Mechanism and Guidance Strategy[M]. Beijing: Science Press,2016:10-13. [5] AGATZ N, ERERA A, SAVELSBERGH M, et al. Optimization for dynamic ride-sharing: a review [J]. European Journal of Operational Research, 2012, 223(2): 295-303. [6] TANG L A, ZHENG Y, YUAN J, et al. A framework of traveling companion discovery on trajectory data streams [J]. ACM Transactions on Intelligent Systems & Technology, 2014, 5(1):1-34. [7] TA N, LI G, ZHAO T, et al. An efficient ride-sharing framework for maximizing shared route [J]. IEEE Transactions on Knowledge and Data Engineering, 2018, 30(2): 219-233. [8] LI X, CEIKUTE V, JENSEN C S, et al. Effective online group discovery in trajectory databases [J]. IEEE Transactions on Knowledge and Data Engineering, 2013, 25(12):2752-2766. [9] KHAN A K M, CORREA O, TANIN E, et al. Ride-sharing is about agreeing on a destination[C]// Proceedings of the 25th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. New York: ACM, 2017: 6. [10] REZA R M, ALI M E, CHEEMA M A. The optimal route and stops for a group of users in a road network [J]. ArXiv Preprint, 2017, 2017: 1706.07829. [11] 李妍峰,高自友,李軍.基于实时交通信息的城市动态网络车辆路径优化问题[J].系统工程理论与实践,2013,33(7):1813-1819.(LI Y F, GAO Z Y, LI J. Vehicle routing problem in dynamic urban network with real-time traffic information [J]. Systems Engineering — Theory & Practice, 2013, 33(7):1813-1819.) [12] GHOSEIRI K, HAGHANI A E, HAMEDI M, et al. Real-time Rideshare Matching Problem [M]. Berkeley: Mid-Atlantic Universities Transportation Center, 2011:21-30. [13] VANOUTRIVE T, VIJVER E V D, MALDEREN L V, et al. What determines carpooling to workplaces in Belgium: location, organization, or promotion? [J]. Journal of Transport Geography, 2012, 22(2):77-86. [14] BAKKAL F, EKEN S, SAVAS N S, et al. Modeling and querying trajectories using Neo4j spatial and TimeTree for carpool matching[C]// Proceedings of the 2017 IEEE International Conference on Innovations in Intelligent Systems and Applications. Piscataway, NJ: IEEE, 2017:219-222. [15] GUTTMAN A. R-trees: a dynamic index structure for spatial searching [C]// Proceedings of the 1984 ACM SIGMOD International Conference on Management of Data. New York: ACM, 1984: 47-57. [16] TAO Y, PAPADIAS D. Efficient historical R-trees[C]// Proceedings of the 13th International Conference on Scientific and Statistical Database Management. Washington, DC: IEEE Computer Society, 2001: 223. [17] TAO Y, PAPADIAS D. The MV3R-tree: a spatio-temporal access method for timestamp and interval queries[C]// Proceedings of the 27th International Conference on Very Large Data Bases. Madison: Morgan Kaufmann, 2001: 431-440. [18] SILVA Y N, XIONG X, AREF W G. The RUM-tree: supporting frequent updates in R-trees using memos[J]. The International Journal on Very Large Data Bases, 2009, 18(3): 719-738. [19] XIONG X, MOKBEL M F, AREF W G. LUGrid: update-tolerant grid-based indexing for moving objects[C]// Proceedings of the 2006 International Conference on Mobile Data Management. Washington, DC: IEEE Computer Society, 2006: 13. [20] SALTENIS S, JENSEN C S, LEUTENEGGER S T, et al. Indexing the positions of continuously moving objects [J]. ACM SIGMOD Record, 2000, 29(2):331-342. [21] TAO Y, PAPADIAS D, SUN J. The TPR*-tree: an optimized spatiotemporal access method for predictive queries[C]// Proceedings of the 29th International Conference on Very Large Data Bases. [S.l.]: VLDB Endowment, 2003: 790-801. [22] ASSENT I, WICHTERICH M, KRIEGER R, et al. Anticipatory DTW for efficient similarity search in time series databases[J]. Proceedings of the VLDB Endowment, 2009,2(1):826-837,. [23] VLACHOS M, KOLLIOS M, GUNOPULOS D. Discovering similar multidimensional trajectories[C]// Proceedings of the 2002 International Conference on Data Engineering. Piscataway, NJ: IEEE, 2002: 673-684. [24] CHEN L, NG R. On the marriage of LP-norms and edit distance[C]// Proceedings of the Thirtieth International Conference on Very Large Data Bases. [S.l.]: VLDB Endowment, 2004: 792-803. [25] FRENTZOS E, GRATSIAS K, THENODORIDIS Y. Index-based most similar trajectory search[C]// Proceedings of the 2007 IEEE 23rd International Conference on Data Engineering. Piscataway, NJ: IEEE, 2007: 816-825. [26] SANKARARAMAN S, AGARWAL P K, MOLHAVE T, et al. Model-driven matching and segmentation of trajectories[C]// Proceedings of the 21st ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. New York: ACM, 2013: 234-243. [27] 潘理,吳鹏,黄丹华.在线社交网络群体发现研究进展[J].电子与信息学报,2017,39(9):2097-2107.(PAN L, WU P, HUANG D H. Reviews on group detection in online social networks[J]. Journal of Electronics & Information Technology, 2017, 39(9):2097-2107.) [28] TA N, LI G L, XIE Y Q. Signature-based trajectory similarity join [J]. IEEE Transactions on Knowledge and Data Engineering, 2017, 29(4): 870-883. [29] SU H, ZHENG K, HUANG J, et al. Calibrating trajectory data for spatio-temporal similarity analysis[J]. The VLDB Journal, 2015, 24(1), 93-116. [30] DUAN Z, TANG L, GONG X, et al. Personalized service recommendations for travel using trajectory pattern discovery [J]. International Journal of Distributed Sensor Networks, 2018, 14(3):155014771876784. [31] TODORIDIS Y, VAZIRGIANNIS M, SELLIS T. Spatio-temporal indexing for large multimedia applications[C]// Proceedings of the Third IEEE International Conference on Multimedia Computing and Systems. Piscataway, NJ: IEEE, 1996: 441-448. [32] ROUSSOPOULOS N, KELLEY S, VINCENT F. Nearest neighbor queries[C]// SIGMOD 95: Proceedings of the 1995 ACM SIGMOD International Conference on Management of Data. New York: ACM, 1995: 71-79.
