基于八叉树的三维室内地图数据快速检索方法

吕宏武 付俊强 王慧强 李冰洋 袁泉 陈诗军 陈大伟

摘 要：针对室内三维地图中数据检索效率不高的问题，提出了一种基于八叉树的室内三维地图数据检索方法。首先，根据八叉树的场景分割方法对数据进行存储;然后，对数据进行编码以方便寻址;其次，为数据添加房间隔断约束条件对检索数据进行筛选;最后，对室内地图数据进行检索。与不具有约束条件的搜索方法相比，搜索代价平均降低了25个百分点，且搜索时间更加稳定。所提方法可以显著地提高室内三维地图数据的应用效率。

关键词：三维室内地图;地图数据;八叉树;邻居搜索;封闭性约束

中图分类号： TP391

文献标志码：A

Abstract： To solve the low efficiency problem of data retrieval in indoor three-dimensional （3D） maps， an indoor 3D map data retrieval method based on octree was proposed. Firstly， the data was stored according to the octree segmentation method. Secondly， the data was encoded to facilitate addressing. Thirdly， the search data was filtered by adding a room interval constraint to the data. Finally， the indoor map data was retrieved. Compared with the search method without constraints， the search cost of the proposed method was reduced by 25 percentage points on average， and the search time was more stable. Therefore， the proposed method can significantly improve the application efficiency of indoor 3D map data.

Key words： 3D indoor map; map data; octree; neighbor search; closedness constraint

0 引言

现如今，人们日常生活中的很多方面都需要地图的支持，这些地图的形式有纸质地图、电子地图以及三维地图等，无论是哪种形式的地图，其使用效率一直是用户所关心的问题。地图数据的检索在地图数据更新、定位、导航呈现、动态路径规划与网元布局等地图技术基础领域具有不可或缺的作用。张永玉等[1]指出传统的数据搜索方法，只是将数据进行简单的存储，并没有使用任何数据结构，这样造成的结果就是无论在搜索时间上还是搜索稳定性上都不是很理想，而室内环境具有数据多变、物体繁多且体积较小的特点，在此环境下，传统搜索方法的缺点无疑被再一次放大，因此，如何对三维室内地图数据进行快速的检索是一个十分有价值的研究课题。

在室外环境下，为了提高地图数据的检索效率，常常采用图幅分幅的方式，其将地图想象成一个俯视图平面，然后对此平面进行网格划分，但对于三维室内地图来说，分幅方法无法解决以下两个问题：一是室内数据过于密集且分布不均，使用分幅方法不容易规定分幅比例，且会出现全部数据挤在一个图幅中而其他图幅空闲这种极端情况;二是分幅方式无法体现三维地图的多楼层问题，而对每一个楼层都进行一次分幅又显得过于繁琐，因此室外地图的分幅方法在室内环境下的表现并不是很好。

由于以上原因，本文提出了一种新的检索方法，其采用由Meagher[2-3]提出的在三维模型处理中常常被使用到的八叉树的概念，对三维室内场景进行规则的划分，并利用八叉树的规则划分特点，采用邻居搜索的方法提高数据的检索效率;同时由于室内环境隔断较多，各个房间相互封闭的特点，本文对Aizawa等[4]所提出的方法进行改进，使其在搜索代价上有所改进。本文所提出的方法，与传统的方法相比具有时间效率和检索稳定性方面的优势，同时也对八叉树邻居检索的效率进行了提高。

1 地图场景划分

八叉树作为一种空间数据结构，由Meather[2-3]在1982年首次提出，是二维空间中的四叉树结构在三维立体空间中的扩展，其作用主要是对三维环境与物体进行存储。Vo等[5]指出，八叉树将三维室内地图的整体场景作为树模型的根节点，每次将场景划分为8份或0份，节点有三种颜色：白色代表该节点区域没有数据;灰色代表该区域包含至少两个物体数据;黑色代表该区域有一个或两个物体数据，其中白色与黑色可以作为叶子节点，灰色代表要进行进一步划分。Vespa等[6]指出这种划分是一个递归的过程，其停止条件是所有节点都是叶子节点或达到规定的划分层数。图1对一个2层树进行了表示，其中图1（a）从三维立方体的角度展示，图1（b）从树型结构的角度展示，白色圆圈代表物体，在46中有两个物体。

Wang等[7]指出，在八叉树结构中，一个节点的邻居节点最多有26个邻居节点，共分为三种情况：面邻居、边邻居与点邻居，如图2所示。图3对点q在每个方向上的邻居节点进行了分类展示，其中a代表面邻居共有6个，b代表边邻居共有12个，c代表点邻居共有8个[8]。

寻址编码使用一个7元组，对划分出的8个子节点进行标记。其中编码的位数与所在层数n相同，记录此节点到根节点的路径，利用“push back”的方法，通过不斷向编码后7元组编码的方式来实现，图1对应的寻址编码的一部分为Pavez与Gómez-Pau提出的概念[9-10]：

2 存储结构的创建

2.1 近似表达

Ummenhofer等[11]指出由于三维场景与三维对象较为复杂且不规则，所以在将一个三维地图数据存储在八叉树结构中时，需要对三维数据进行近似表达，这种近似表达的效果可以通过包装盒来实现。Steinbrücker等[12]将包装盒分为包装球（bounding sphere）、轴对齐包装盒（Axis Aligned Bounding Box，AABB）与定向包装盒（Optimized or oriented Bounding Box，OBB）。由于室内地图场景的模型方形的较多，所以本文不采取包装球的近似表达方法。另一点，Wang等[13]指出OBB实施起来很复杂，且执行速度慢，其主要应用于光线追踪与碰撞检测方面;而AABB实施简单，精确度高，主要应用于游戏场景的物体近似表达，所以，综合比较场景特性与实施代价，本文选取AABB进行室内地图中三维物体对象的近似表达。如图4所示，本文以一个电脑椅为例，利用AABB进行包围，具有如下数据与结论：

1）A点坐标（2，3，2）;

2）B点坐标（10，10，18）;

3）A与B可以看成AABB的最小点与最大点，两者可以包裹成一个范围，则根据A，B的坐标可以得出，{点在AABB包装盒内|2≤x≤10，3≤y≤10，2≤z≤18};

4）采用A、B两点即可对包装盒进行表示。

当进行八叉树分割时，有可能将物体进行分割，本文将这种情况下物体尝试存储在其父节点中，所以本文中的结构，不仅仅在叶子节点中有数据存在。

2.2 存储模型结构

在方法1中详细介绍了3个用来表示八叉树存储模型的结构体，它们功能各不相同，但是之间又具有联系，同时八叉树的构建伪代码如方法2所示。

Tree_Node表示八叉树的节点，主要为坐标、位置编码与包含的物体;Room表示各个房间的信息，主要为房间号和房间范围坐标;Object表示各个物体的信息，主要为物体号、AABB与所在房间号;联系表示TreeNode与Object通过objectID相联系，Object与Room通过roomId相联系。

3 搜索方法

三维室内地图的数据具有更新频繁、数据量大的特点。当进行地图数据更新，对室内的一个物体进行移动、更换与删除等操作时，其周围的一些物体通常也会因此而发生变化，并且发生变化的多数只是同一个房间内的物体;当进行导航呈现时，对于一个数据的呈现同时，也会将其周围的地图数据呈现出来，这种情况在室外导航地图很常见，而对于室内地图来说同样具有这种情况，不过是在此基础上呈现的是同一房间内的地图数据。不仅仅是这两种应用，对于地图的很多必要功能比如网元布局与路径规划等，都具有这种“搜一点，遍及周围”的情况存在。

根据以上情况的特点，本文提出利用邻居搜索的方式，当搜索地图数据时，利用八叉树规则划分的特点，直接进行邻居节点的计算，得到邻居节点后进行计算得到节点中的地图数据，从而得到目标数据周围的数据，这些数据是真实有用的，可以减少反复搜索的次数，从而达到优化地图数据的目的。Schrack[14]在1992提出了一种计算四叉树与八叉树邻居的方法，但其只能计算处于同一树深度的邻居;Aizawa等[4]在此基础上进行了改进，不再受树深度的影响;Namdari等[15]提出了在构建树结构的同时将邻居信息进行搜索，这一过程并不会对树结构的构建增添任何复杂性。本文在此基础上，根据室内地图数据搜索的特点，提出了房间隔断的约束，使其在进行邻居搜索时，对于处于不是同一封闭地图数据，不再进行显示，这使得搜索在代价上有所提高。下面通过一个具体例子来说明这一搜索过程。

例1 本文以图1（a）为例子，其中划分层数为2。

步骤1 本文假设根节点为root，利用方法1中的算法，完成了八叉树的构建与地图场景的划分，这时需要在树的构建过程中确定节点45的邻居。

步骤2 利用图7与图8中的算法对应表1和表2，计算45与46，得到：利用式（1）与式（2）对应表1和表2，计算45、46与47得到：

图名在正文中，要依照编号的先后顺序引用，不能跳跃式引用。此处建议改为别的语句描述，或写某个具体的名称。另外，文中也没有图8

计算八叉树的八个子节点的计算如式（3），设父节点坐标为（x（f），y（f），z（f）），则子节点坐标为：

z（c）∈{z（f），z（f）+length，z（f）-length}}（3）这个公式这样排正确吗？是否符合表达，原来的表达感觉不符合规范。回复：正确

其中：x（c）为所求子节点的x坐标，x（f）为父节点的x坐标，y坐标与z坐标同理，length为子立方体的尺寸。

步骤4 查看45，46，47中物体所在房间号是否相同，得出，45与46中的物体所在房间号相同，则46为45的邻居，47则不是，将46中的该物体放到45的邻居物体表中。

步骤5 查看45的父节点以及45的邻居46的父节点，它们中的物体所在的房间号，得出46的父节点中的物体f也在房间3中，所以物体f也放到45的邻居物体表中。

对于邻居节点的判定如式（4）～（6）所示，本文以判断编码为a和b的节点为例。

若a和b满足式（4）中6种情况中的一种，则两者为面邻居：

同理a与b在y或z上差length的情况类似，共6种情况。

若a和b满足式（5）中12种情况中的一种，则两者为边邻居：

同理a与b在yz或xz上同时差length的情况类似，共12種情况。

若a和b满足式（6）中8种情况中的一种，则两者为点邻居：

4 实验与分析

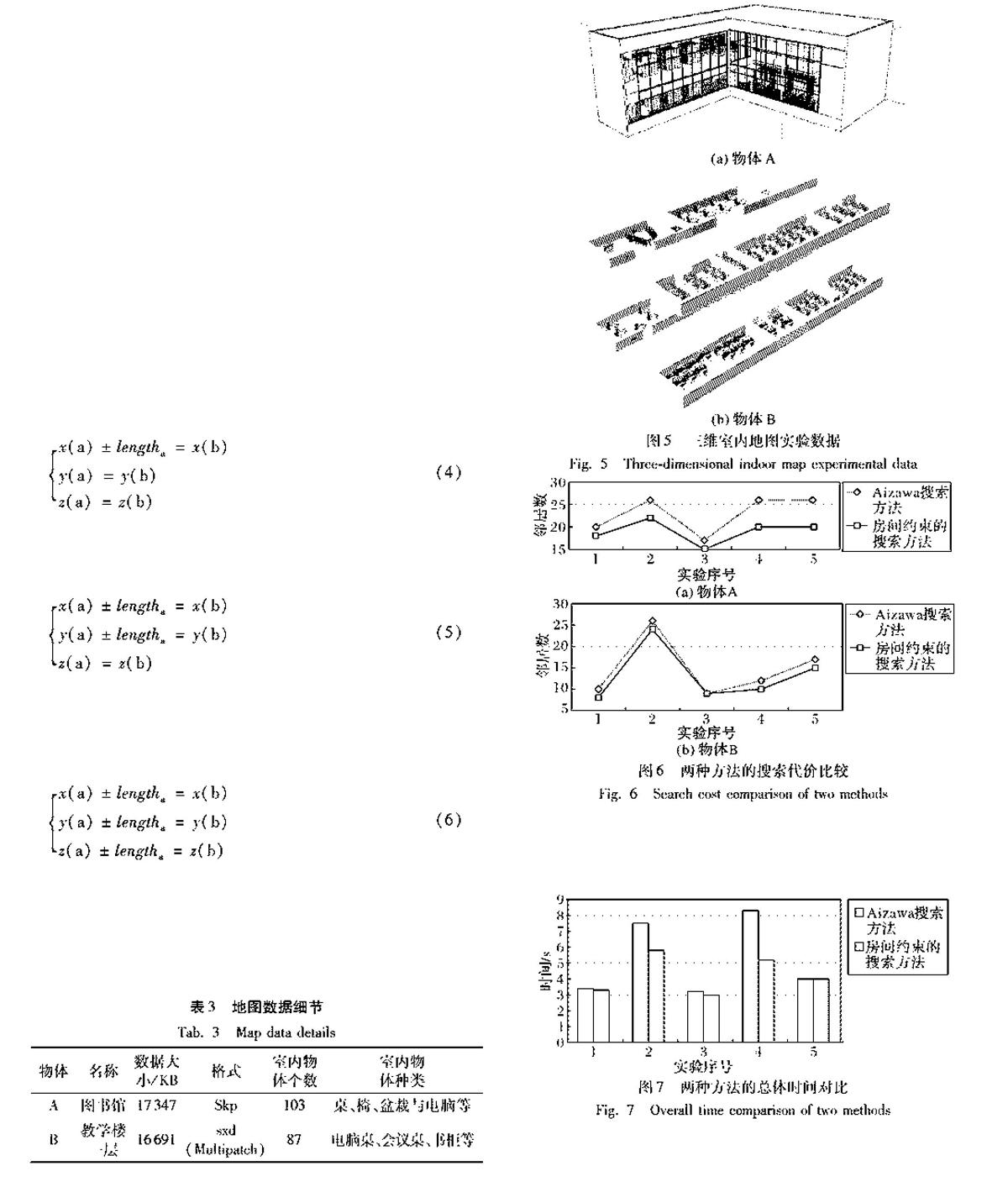
本文以SketchUp與ArcGIS文件作为实验的数据，如图5所示，物体A与物体B为三维室内地图，具体细节参见表3所示。根据Namdari等[15]和王永志等[16]的分析得出，当不采用任何数据结构与搜索方法对三维室内地图进行搜索时，搜索的时间复杂度是O（np），其中n为数据的个数，p为目标数据周围有用数据的个数。付仲良等[17]指出当仅采用八叉树划分法对实验数据进行标准划分，而不采用任何搜索方法，由于经典八叉树无法找到邻居地址，所以此时搜索的时间复杂度是O（23（L-1）），其中L为树的深度。肖怡等[18]指出当采用八叉树划分，并采用Schrack[14]提出的搜索算法时，搜索的时间复杂度为O（L）。当采用八叉树数据结构进行划分，并采用Aizawa等[4]所提出的邻居搜索算法进行搜索，由于其利用八叉树划分的规则性特点，可以通过公式计算出目标数据周围最多26个邻居地图数据，这能够满足地图应用中，对于目标地图数据的周围数据进行呈现的需求，即“搜一点，遍及周围”的情况，这会减少对于地图数据的搜索次数，这种应用背景下的搜索时间复杂度会保持在O（1）。同理若采用本文提出的带房间约束条件的邻居搜索方式进行物体的搜索，则搜索的时间复杂度也是O（1），因此采用八叉树结构的邻居搜索方式对室内地图数据搜索进行改善，在时间复杂度上有所降低，且不会随着树的深度的增加而变得更复杂。

Aizawa等[4]所提出的方法在时间效率上已经达到了很好的效果，但是对于室内地图这种独立封闭性空间较多的三维场景来说，在每次搜索代价上就显得有些笨重，而本文提出的房间隔断约束条件，可以很好地改善这一点，实验结果如图6所示，结果表明此方法实际可行，且在房间约束条件下，多数情况下的搜索代价都有所改善。

由于本文提出的方法，在搜索代价方面有所改善，所以结合对于搜索结果的分析成本，总体来说时间上也有所降低，如图7所示。

5 结语

本文提出了一种应用于三维室内地图场景的数据搜索方法，主要目的是解决室内地图数据的存储效率较低与检索速度较慢的问题。其原理为利用八叉树结构对场景进行划分，这与传统分幅存储方法相比具有更高的检索效率;同时根据室内地图应用中普遍存在的“搜一点，遍及周围”的这种区域需求的情况，提出邻居搜索模型，并结合室内环境相对封闭的特点，添加了封闭性约束条件从而对邻居搜索模型进行改进。实验结果表明，本文提出的搜索方法，可以将时间复杂度保持在O（1），具有良好的稳定性，不会因为数据的增多、划分层数的增加而出现波动;在搜索代价方面，受封闭性约束条件的限制，相比Aizawa等[4]提出的算法也得到了改善。

下一步工作中将在设计节点结构时考虑更为复杂的场景，使其适用更多的更复杂的室内环境。

参考文献 （References）

[1] 张永玉，马劲松.3DGIS中线性八叉树空间索引的建立与查询算法研究[J].计算机工程与科学，2009，31（2）：61-63.（ZHANG Y Y， MA J S. Research on establishment and query algorithm of linear octal tree spatial index in 3DGIS[J]. Computer Engineering and Science， 2009， 31（2）： 61-63.）

[2] MEAGHER D. Geometric modeling using octree encoding[J]. Computer Graphics and Image Processing， 1982， 19（2）： 129-147.

[3] MEAGHER D. The octree encoding method for efficient solid modeling[D]. Troy， NY： Rensselaer Polytechnic Institute， 1982.

[4] AIZAWA K， TANAKA S. A constant-time algorithm for finding neighbors in quadtrees[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2009， 31（7）： 1178-1183.

[5] VO A V， TRUONG-HONG L， LAEFER D F， et al. Octree-based region growing for point cloud segmentation[J]. ISPRS Journal of Photogrammetry and Remote Sensing， 2015， 104： 88-100.

[6] VESPA E， NIKOLOV N， GRIMM M， et al. Efficient octree-based volumetric SLAM supporting signed-distance and occupancy mapping[J]. IEEE Robotics and Automation Letters， 2018， 3（2）： 1144-1151.

[7] WANG K， FU H， PENG S， et al. A RDF data compress model based on octree structure[C]// Proceedings of the 2017 12th IEEE Conference on Industrial Electronics and Applications. Piscataway， NJ： IEEE， 2017： 990-994.

[8] WONG H T T， HUANG Y， TSANG S C， et al. Real-time model slicing in arbitrary direction using octree[C]// Proceedings of the ACM 44th International Conference on Computer Graphics and Interactive Technique. New York： ACM， 2017： Article No. 9.

[9] PAVEZ E， CHOU P A. Dynamic polygon cloud compression[C]// Proceedings of the 2017 IEEE International Conference on Acoustics， Speech and Signal Processing. Piscataway， NJ： IEEE， 2017： 2936-2940.

[10] GMEZ-PAU ， BALADO L， FIGUERAS J. Detectability of structural defects using octree encoding[C]// Proceedings of the 2017 32nd Conference on I/Design of Circuits and Integrated Systems. Piscataway， NJ： IEEE， 2017： 1-6.

[11] UMMENHOFER B， BROX T. Global， dense multiscale recon-struction for a billion points[C]// Proceedings of the 2015 IEEE International Conference on Computer Vision. Piscataway， NJ： IEEE， 2015： 1341-1349.

[12] STEINBRCKER F， STURM J， CREMERS D. Volumetric 3D mapping in real-time on a CPU[C]// Proceedings of the 2014 IEEE International Conference on Robotics and Automation. Piscataway， NJ： IEEE， 2014： 2021-2028.

[13] WANG P S， LIU Y， GUO Y X， et al. O-CNN： octree-based convolutional neural networks for 3D shape analysis[J]. ACM Transactions on Graphics， 2017， 36（4）： 72.

[14] SCHRACK G. Finding neighbors of equal size in linear quadtrees and octrees in constant time[J]. CVGIP： Image Understanding， 1992， 55（3）： 221-230.

[15] NAMDARI M H， HEJAZI S R， PALHANG M. MCPN， octree neighbor finding during tree model construction using parental neighboring rule[J]. 3D Research， 2015， 6（3）： 29.

[16] 王永志，杨路生，廖丽霞，等.八叉树与三维R树集成的激光点云数据存储结构[J].地球信息科学学报，2017，19（5）：587-594.（WANG Y Z， YANG L S， LIAO L X， et al. Laser point cloud data storage structure integrated with octree and 3D R-tree[J]. Journal of Earth Information Science， 2017， 19（5）： 587-594.）

[17] 付仲良，刘思远，田宗舜，等.基于多级R-tree的分布式空間索引及其查询验证方法研究[J].测绘通报，2012（11）：42-46.（FU Z L， LIU S Y， TIAN Z S， et al. Research on distributed spatial index and its query verification method based on multi-level R-tree[J]. Bulletin of Surveying and Mapping， 2012（11）： 42-46.）

[18] 肖怡，李佳田，张文靖，等.一种自然邻近关系查询的空间索引结构[J].地理信息世界，2018，25（1）：32-38.（XIAO Y， LI J T， ZHANG W J， et al. A spatial index structure of natural neighbor relational query[J]. Geomatics World， 2018， 25（1）： 32-38.）