SQM：基于Spark的大规模单图上的子图匹配算法

李龙洋 董一鸿 施炜杰 潘剑飞

摘 要：针对大规模数据图下基于回溯法的子图查询算法的准确率低、开销大等问题，为提高查询准确率，降低大图下的查询开销，提出一种基于Spark的子图匹配（SQM）算法。首先根据结构信息过滤数据图，再将查询图分割成基本查询单元;然后对每一个基本查询单元分别匹配后进行Join操作;最后运用并行化提高了算法的运行效率，减小了搜索空间。实验结果表明，与Stwig、TurboISO算法相比，SQM算法在保证查询结果不变的情况下，速度提高了50%这个“最多”应用的不好，与两种算法相比，需分别写明确提高了多少。英文摘要处作相应修改。

关键词：子图匹配;图分割;大规模单图;并行化;Spark

中图分类号： TP392

文献标志码：A

Abstract： Focusing on low accuracy and high costs of backtracking-based subgraph query algorithm applied to large-scale graphs， a Spark-based Subgraph Query Matching （SQM） algorithm was proposed to improve query accuracy and reduce query overhead for large graphs. The data graph was firstly filtered according to structure information， and the query graph was divided into basic query units. Then each basic query unit was matched and joined together. Finally， the algorithms efficiency was improved and search space was reduced by parallelization. The experimental results show that compared with Stwig （Sub twig） algorithm and TurboISO algorithm， SQM algorithm can increase the speed by 50% while ensuring the same query results.

Key words： subgraph matching; graph segmentation; single large-scale graph; parallelization; Spark

0 引言

現实生活中，作为一个重要的数据结构，图挖掘在社交网络、Web图和生物化学领域都有广泛的应用。子图匹配是图挖掘中一个重要的分支，用于从社会网络中寻找频繁子图以揭示节点间的关联信息，也可以通过计算三角形个数，判定社交网络的聚集程度。随着互联网行业的飞速发展，图结构的规模不断扩大。根据国家互联网信息中心统计[1]，截止到2016年12月，中国网民规模7.31亿，网站总数为482万，网页数达到了2360亿，网页长度总字节数达到了13PB。如何对大规模的单图模型中的子图匹配进行有效的分析和处理是目前面临的严峻挑战。

大量的子图匹配研究，集中在图规模较小的数据单图或图集[2]，大规模单图上的子图匹配问题被证明是一个NP（Non-deterministic Polynomial）-hard问题。最经典的算法为Ullmann[3]提出的Ullmann算法，采用深度优先搜索方法依次找出同构子图，Cordella等[4]提出了VF2算法，该算法在Ullmann算法的基础上增加了剪枝操作和搜索匹配，提高了算法的运行效率。GraphQL（Graph Query Language）算法[5]根据邻接状态和深度信息进行剪枝操作提高算减小法的时间开销，GADDI（an index based graph matching algorithm in a single large graph请补充GADDI的英文全称。回复：对于文中GADDI的英文全称修改为GADDI（an index based graph matching algorithm in a single large graph））算法[6]通过构建邻接辨别子结构距离来过滤备选节点，两者都是基于回溯法得到候选子图来完成子图匹配工作。张硕等[7]提出的COPESl（COmmon PrEfix tree Subgraph Isomorphism）算法中，提出一种图集压缩组织方法，将多个图结构化地组织起来，并给出一个基于图挖掘的索引特征生成方法。TurboISO（Towards ultraFast and robust subgraph ISOmorphism）[8]算法通过将查询图构建成NEC-Tree（Neighborhood Equivalence Class-Tree）结构形式来减小候选节点范围，通过进行深度优先搜索匹配，并行性差。这些方法都仅适用于小规模的单图或图集，无法满足大规模数据图的子图匹配需求。

近年来，文献[9-10]使用Map-Reduce思想并行化子图进行匹配工作，将查询图按边划分为基本单元，在匹配过程中大量的Join操作以及大规模数据图的分布不均都导致算法无法在并行环境有效运行。Stwig（Sub twig）[11]运行在微软图形数据库Trinity上，将查询图分割为Stwig作为基本查询单元，然而，大量的Join操作和大规模数据图的划分不均匀依然是目前并行算法的瓶颈。

为了克服解决单机算法无法处理大规模单图，而并行化处理大规模单图所遇到的大量Join操作和无效匹配的缺点问题，本文提出了一种基于Spark的大规模单图的子图匹配（Spark-based Subgraph Query Matching， SQM）算法，主要贡献如下：1）传统的子图匹配算法随机对查询图进行划分，本文则根据查询图节点的度以及各节点在数据图上的出现频次，划分为SubQ（Subgraph Query子查询）查询单元进行子图匹配，同时对原始数据图进行剪枝操作，过滤不满足条件的数据图顶点和边，并对SubQ查询单元匹配顺序和Join顺序进行优化，减少了网络通信和无效匹配，提出了一种基于Spark的大规模单图的子图匹配算法。2）对比实验显示，针对不同的查询图，在不同的数据集上，SQM算法运行效率都是最高。

1 相关工作

在社交网络中，实体和实体之间的关系可以使用图结构表示：对具有特定关系的人或团体的查询可以转换为在一个大规模单图上节点查询或子图匹配问题;在生物领域，可以通过已知性质的蛋白质结构的查询，快速地找出未知结构的蛋白质和基因的结构和性质，为研究生物医学领域提供技术支持[12]文后的文献[2]与文献[12]是同一个文献，请作相应调整，因为在正文中的引用文献的顺序是依次进行的，所以建议将文献[2]（或[12]）改为另外一条文献，注意彼此间不要再重复了。特别要注意正文中的引用顺序和语句调整。。已有的子图匹配工作可以归纳为四类[12]。

1）无索引结构。最基本的子图匹配算法Ullmann[23]此处应该是文献3吧？请明确和VF2[34]这个是指代哪个文献，请明确。都是无索引结构的子图匹配算法。Ullmann算法使用深度优先搜索算法进行匹配，而VF2算法在此基础上增加了剪枝和匹配顺序的优化，两者只适用于规模很小的数据图。TurboISO[7]算法则是通过使用广度优先搜索将查询图构造成NEC-Tree，在匹配的过程中，使用深度优先搜索的方式进行查询图的匹配;但是并行性较差，无法满足大规模单图的子图匹配查询需求。并行化算法Stwig[11]，运行在微软图形数据库Trinity上，将查询图划分为Stwigs基本查询单元，对每一个Stwigs基本单元分别匹配，最后将其中间结果进行合并操作，GaoZou等[913]文献9的作者不是Gao，请依照引用顺序进行依次调整。提出了并行化解决top-k子图查询问题，对数据图进行近似图模拟的同时对查询图各顶点进行并行化匹配后进行连接操作，大量的Join操作导致算法开销大，在大规模单图上无效有效处理。

2）边/节点索引结构。为了能够用SPARQL查询RDF（Resource Description Framework请补充RDF的英文全称）数据，RDF-3X（for RDF Triple eXpress）[1314]和BitMat （Bit-Matrix）[1415]等算法使用边作为索引，SPARQL查询将查询图分解为边，各自匹配后进行连接操作。大量的连接操作使得算法运行效率差，且SPARQL只能表示为查询图的子结构，后期仍需合并操作。Hong等[1516]提出了對查询图和数据图节点进行索引，通过节点集合相似和结构相似进行剪枝，而对顶点和结构构建索引时空开销大，后期需合进行大量的Join操作，无法有效进行匹配。

3）频繁子图索引。为了避免大量的Join操作，Yan等[1617]找出频繁子图或频繁查询子结构后进行频繁结构索引操作。该类方法的缺点在于找出频繁子图的过程是一个时间开销非常大的操作，而且频繁子图数过多，也会带来索引太大，同时不能进行非频繁子结构的查询图的子图匹配操作。

4）邻居索引。GraphQL[4]和GADDI[6]等算法通过找出全局或者局部邻接来构建索引。对于每一个节点v，GraphQL算法对其构建以v为圆心、半径为r的子图索引结构，而GADDI算法则是通过对最短路径长度小于L的节点进行两两组合，构建出索引结构。该类算法需要构建一个复杂的数据结构，时间开销大，无法在大规模图上使用。

2 基本概念

3 基于Spark的大规模单图子图匹配算法——SQM算法

3.1 内存分布式计算框架——Spark

Spark[1718]是UC Berkeley AMP lab开源的类Hadoop通用的并行计算框架，基于Hadoop MapReduce算法实现分布式计算，核心为弹性分布式数据集（Resilient Distributed Dataset， RDD），是一个容错的、并行的数据结构，可以让用户显性地将数据存储到磁盘和内存中，并能控制数据的分区。RDD上主要有Transformation和Action两种类型的操作，并且当前的RDD都与前一个RDD有依赖关系，Spark在运行作业的过程中会将多个RDD串联起来形成一个有向无环图（Directed Acyclic Graph， DAG），可以很好地高效运行，拥有Hadoop所具有的优点;但不同于Hadoop将Job中间输出和结果保存在HDFS（Hadoop Distributed File System），而将其直接保存在内存中，且除了能够提供交互式查询外，它还可以优化迭代工作负载，因此Spark能更好地适用于数据挖掘与机器学习等需要迭代的MapReduce算法[1819]。

3.2 子图匹配算法—SQM

SQM算法是基于RDD设计，首先将给定的查询图分解，划分为基本查询单元SubQ的同时对数据图进行剪枝操作，通过依次匹配得到各自的匹配结果，最后进行Join操作，得到最终的结果。

1）剪枝。

在大规模单图上进行子图匹配是一个NP-Hard问题，因此，需要对查询图和数据图作处理才能更好地满足匹配要求，对于数据图，根据查询图各顶点标签的度与数据图相同标签的顶点的度的对比，将数据图上相同标签的顶点的度小于查询图上各顶点的度的顶点过滤，并去除顶点标签不在查询图的顶点标签中。

例1查询图如图1（b）所示，一共有5个标签：a、b、c、d、e，度分别为2、4、1、2、4。数据图如图1（a）所示，包含a、b、c、d、e、f共6个标签，标签f对应顶点1006在匹配过程中无效，将其去除，同时，1002顶点对应的标签b的度为3，而在查询图上标签b所对应的标签为4，因此1002顶点在匹配过程中无效，将其去除。通过过滤不存在的顶点和数据图顶点度比查询图对应标签的顶点度更小的顶点，图2为经过剪枝的数据图。

2）查询图分解。

当查询图的顶点数过多，不论深度优先搜索还是广度优先搜索，时空复杂度都非常大，在大数据集上无法完成。将查询图分解，分解成多个子结构，每一个子结构的顶点数少，匹配时时空复杂度则会大幅度降低，因此，对于给定的查询图，可以考虑对其进行分割，划分为多个基本查询单元SubQ，将其划分为SubQ的结果如图3所示。

每一个查询图的分解有多种方式，如何制定好的分解策略决定了匹配的时空开销。给定的查询图q，对于每一个顶点v，顶点标签在数据图上出现越频繁，则该节点选择概率则越低，同时该顶点的邻接节点数量越多，则该节点优先匹配的概率越大。

根据其在数据图上的频率freq（v.tag）和节点的度Deg（v），可以计算出各节点被选择的概率s（v）=Deg（v）/freq（v.tag）。根据节点选择概率，找出max（s（v））作为基本查询单元SubQ的root节点，找出其邻接节点，将root节点和邻接节点之间的边去除，在剩余的节点中找出选择概率最大的节点u重复以上操作，直到查询图中的所有顶点和边都去除，则分解完成。

对于图2给定的剪枝后的数据图G和图1（b）给定的查询图q，首先计算出查询图q的各节点（1001，a），（1002，b），（1003，d），（1004，c）和（1005，e）的度分别为Deg（1001）=2，Deg（1002）=4，Deg（1003）=2，Deg（1004）=1，Deg（1005）=1;然后再分别计算出q中各节点的标签a，b，d，c，e在数据图中出现的频繁度freq（a）=2， freq（b）=1， freq（d）=2， freq（c）=1， freq（e）=1。查詢图q中每一个节点的选择概率根据计算公式s（v）=Deg（v）/freq（v.tag）分别为1、4、1、1、1，可以看出（1002，b）选择概率最大，则选择（1002，b）作为第一个SubQ的root节点，同时得到邻接节点为（1001，a）、（1003，d）、（1004，c）和（1005，e），将其作为SubQ的child节点，并从查询图中去除对应边（1002，1001），（1002，1003），（1002，1004）和（1002，1005），查询图剩余边为（1001，1003）。1001，1003的选择概率分别为1，1，则随机选择节点（1001，a）作为下一个SubQ的root节点，同时得到其邻接节点（1003，d）。此时查询图q剩余边为空，划分完成。最终划分的结果如图4所示。

3）匹配操作。

该算法基于RDD操作。在匹配的过程中，对于每一个SubQ，分别在不同的分区上同时匹配。在每一个分区上，不同的查询单元SubQ之间的匹配顺序采用启发式方法，其原则为：1）如果该SubQ中的某一条边的两个节点已被匹配，则优先匹配该边;2）如果都未匹配，则选择概率最大的root节点优先匹配。

其伪代码表示如下。

在匹配过程中，根据各SubQ的产生顺序，设置其SubQ的索引为SubQ（i）。首先，根据各SubQ的root节点的选择概率找出最大的SubQ（i）查询单元进行匹配，当root节点匹配完成后，再分别匹配其child节点，匹配child节点时根据之前计算的选择概率从大到小选择，进一步减少中间结果的计算。当Sub（i）查询单元匹配完成后，下一个选择的SubQ（j）优先考虑其root节点在之前的匹配过程中已匹配完成，然后分别匹配其child节点。如此继续，直到所有SubQ都匹配完成，最终每一个SubQ查询单元都可以得到其匹配集合。

4）Join操作。

对于每一个查询基本单元SubQ，通过以上操作完成各自的匹配结果。如果当前结果为中间结果，需要将中间结果进行Join操作，最终得到查询图q在数据图G中的匹配结果。采用不同的Join顺序，算法运行时间和空间的不同，需要寻找出一个合适的Join顺序来提高算法的运行效率。

采用的Join操作顺序如下：

a）计算出每一个基本查询单元SubQ的匹配个数matchCount和每一个SubQ的child节点的个数chdCount，SubQ的匹配数量越少，剪枝越早，则后期匹配时匹配次数越少，基本查询单元SubQ的child节点的个数越多，匹配越早。

b）对于SubQ的匹配顺序可以按照matchCount/chdCount的比值从小到大进行匹配，匹配时使用Spark的mapPartitions操作使各SubQ的Join过程在各自的分区同时运行，避免了分区之间的通信，提高了算法的运行效率。

4 实验结果与分析

实验使用普通PC 14台，其中1台为主节点，其余13台机器为从节点，每台机器的配置相同：CPU为Core i5，内存为6GB，操作系统为CentOS 6.5，集群环境为基于Hadoop 2.6.5上构建的Spark 1.6.3，运行模式为Spark on Yarn，scala版本为2.10.6，jdk版本为1.8。

数据集采用的是真实数据集，来自于SNAP[1920]描述信息如下。

Aamzon 亚马逊上的商品信息，节点表示商品，用边表示某购物商购买商品u的同时购买商品v，顶点标签分别表示商品类别，由于原始数据集上并不含有顶点的标签且图规模不大，故用5个标签随机对顶点进行标记，标签分布服从高斯分布，为非幂率数据集。

DBLP 该数据集来自于论文作者合作信息，顶点表示作者信息，而顶点标签则表示作者所属研究领域，边则表示某两个作者之间有过合作，该数据集为幂率数据集，顶点规模不大，顶点的标签则是通过使用满足高斯分布的5个随机数进行标记。

LiveJournal 该数据集来自于LiveJournal社交网络，顶点表示社交网络中的人的信息，顶点的标签则表示为社交网络中人所属行业，该数据集中边的信息表示为社交网络中两个人之间有关系。由于原始数据集没有顶点标签信息且顶点规模大，用少量的顶点标签表示所得到的结果过多，因此对其使用服从高斯分布的20个随机数填充其顶点标签。

Twitter 该数据集来自于Twitter社交网络，顶点表示现实生活中的人，顶点标签表示人所属类别，而边则表示两个人之间有关系，原始的数据集并不包含顶点标签且顶点规模为千万级，故使用服从高斯分布的20个随机数来填充顶点标签。

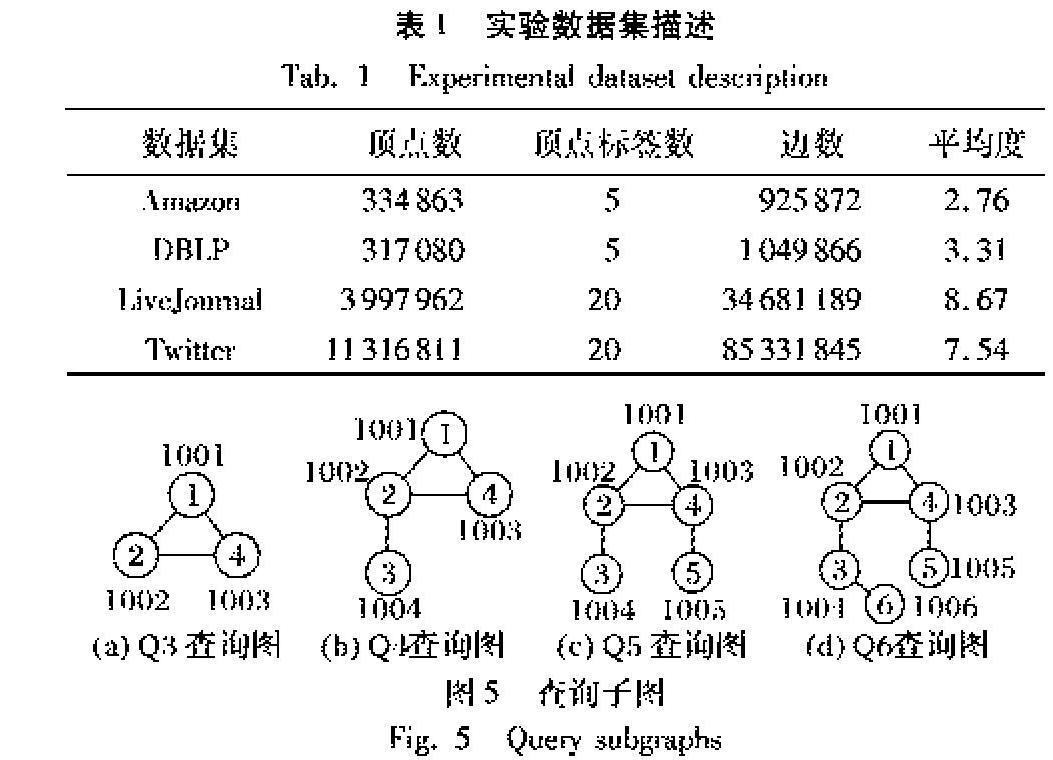
数据图使用表1所示的数据集，查询图使用边数为3，4，5，6的查询图，例如图5所示。

图5共有4种查询子图，边数分别为3，4，5，6。对于每一个数据集，分别使用这4种查询图，每一个都有5个相同边数的查询图，一共20个查询图进行实验，最后运行时间使用平均值。

4.1 SQM算法与其他算法的性能比较

为了评估SQM算法的性能，实验部分选择与下列算法进行比较：

1）Stwig算法是文献[11]中提出的分布式子图匹配算法，该算法将数据图保存在微软Trinity图数据库中。

2）TurboISO算法是文献[7]中提出的算法，该算法为单机子图同构算法。

本文将这两种算法都改造成Spark版本，以保证平台一致性。

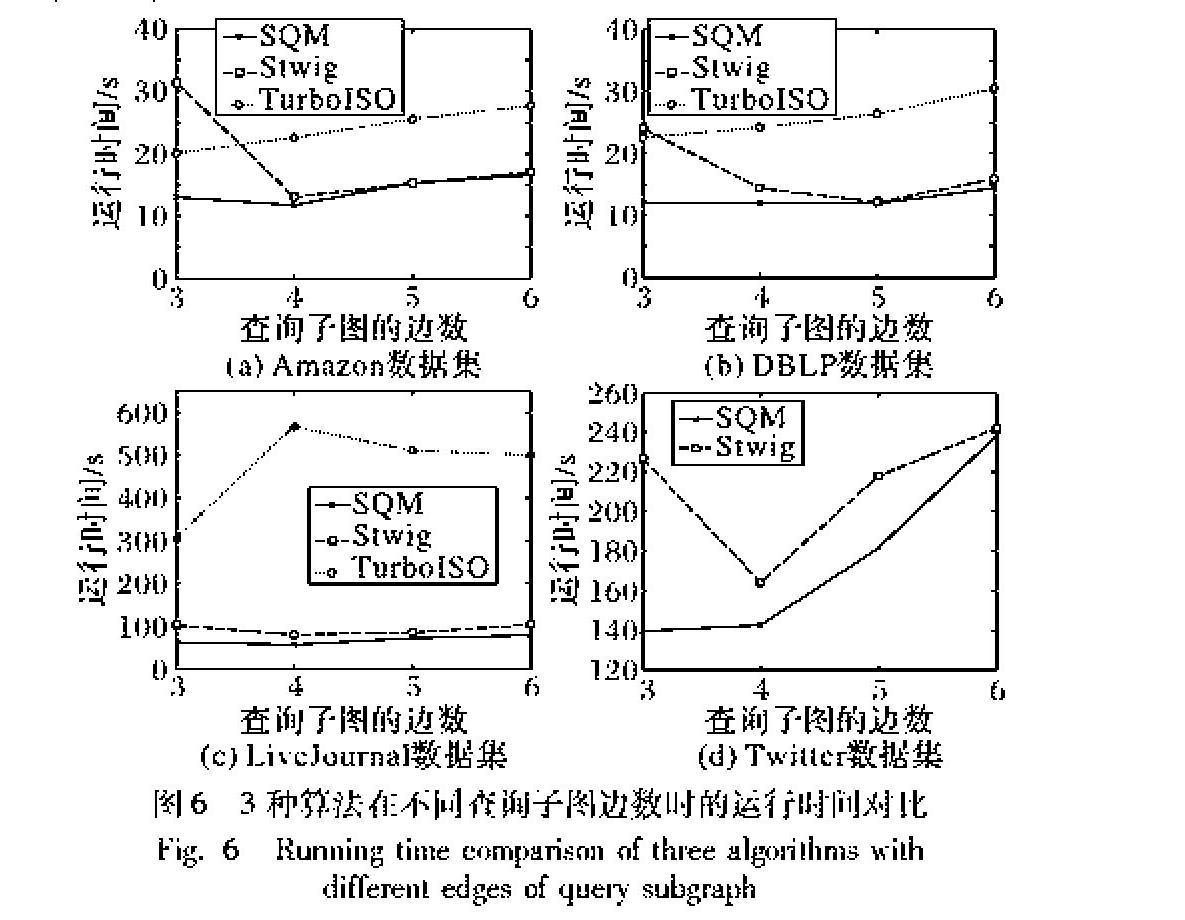
SQM与Stwig算法在不同的数据集上，对比实验结果如图6所示。

SQM算法、Stwig算法与TurboISO算法都运行在14台PC组成的集群上，并行度都设置为14。图6显示了SQM算法的运行效率，横坐标为图5所示的查询子图，横坐标值为图5所示的查询子图的边数，纵坐标是算法运行时间。图6显示：在Amazon數据集和DBLP数据集上，由于数据量并不是很大，3个算法的运行时间相差不大，SQM算法和Stwig算法运行时间相近，而TurboISO算法运行时间则较长;而在LiveJournal数据集，三种算法运行时间相差大，SQM算法时间开销最低，Stwig算法次之，TurboISO算法运行效率最低;最后，在Twitter数据集上，TurboISO算法已经无法运行出结果，SQM算法比Stwig算法运行效率高。实验显示本文提出的SQM算法运行效率最高，这是因为SQM算法采用了合理的分解机制，将查询图分解为基本查询单元，并进行Join顺序优化，减少网络通信开销和无效匹配，大幅度提高了查询的速度。

4.2 不同并行度下SQM算法的性能

除了比较各查询图在不同的数据集下运行时间的对比，本文采用的是基于Spark的分布式环境下子图匹配算法，需要比较在不同的并行度下各数据集的运行情况来制定一个最优的并行度进行子图匹配，结果如图7所示。

图7中，横坐标表示并行度，纵坐标表示运行时间。可以看出随着并行度的增加，在不同的数据集上运行时间都有一个减少到增加的过程，其中的原因是随着并行度的增加，算法运行效率不断提高;但是随着并行度不断增加，各节点之间的通信开销也不断增加。因此，对于每一个数据集，选择一个合适的并行度可以为多种查询图匹配时间进行优化，在子图匹配过程中先运行一个子图同构来选择出最优的并行度，之后针对不同的查询图，都使用该最优并行度作为算法运行并行度，使得算法能够比之前更加优化。图7中，横坐标表示并行度，纵坐标表示运行时间，可以看出随着并行度的增加，在不同的数据集上运行时间都有一个减少到增加的过程，其中的原因是随着并行度的增加，算法运行效率不断提高;但是随着并行度不断增加，各节点之间的通信开销也不断增加，因此，对于每一个数据集，选择一个合适的并行度可以为多种查询图匹配时间进行优化，在子图匹配过程中先运行一个子图同构来选择出最优的并行度，之后针对不同的查询图，都使用该最优并行度作为算法运行并行度，使得算法能够比之前更加优化。

5 结语

本文提出了一个在大规模单图上进行子图匹配（SQM）的算法，该算法运行在基于Spark的分布式环境上，可以处理大规模单图，对于数据图优先进行一个剪枝操作后根据查询图的结构将其分割为基本查询单元SubQ，各查询子单元分别匹配后进行Join操作，在进行Join操作时优化了Join操作顺序以最大化减小匹配次数，大幅度提升了算法的运行效率。通过真实数据集与其他算法进行了实验比较，验证了本文算法的性能。子图匹配问题作为频繁子图挖掘中重要的解决步骤，好的子图匹配算法可以有效提高频繁子图挖掘效率。通过对未知蛋白质和化学结构与已知结构进行比对，可以用于未知蛋白质和化学物质的发现。

参考文献 （References）

[1] 中国互联网信息中心.中国互联网络发展状况统计报告[EB/OL].（2017-02-03）[2018-05-20]. http：//www.cac.gov.cn/2018zt/cnnic41/index.htm.（China Internet Information Center. Statistical Report on the Development of Chinas Internet. [EB/OL]. （2017-02-03）[2018-05-20].http：//www.cac.gov.cn/2018zt/cnnic41/index.htm.）

[2] 于静，刘燕兵.大规模图数据匹配技术综述[J].计算机研究与发展，2015，52（2）：391-409.（YU J， LIU Y B. Summary of large-scale graph data matching technology [J]. Journal of Computer Research and Development， 2015， 52（2）： 391-409.）

KATSAROU F， NTARMOS N， TRIANTAFILLOU P. Performance and scalability of indexed subgraph query processing methods [J]. Proceedings of the VLDB Endowment， 2015， 8（12）： 1566-1577.

文献2与文献12是同一个文献，请作相应调整，因为在正文中的引用文献的顺序是依次进行的，所以建议将文献2（或12）改为另外一条文献，注意彼此间不要再重复了。特别要注意正文中的引用顺序和语句调整。

[3] ULLMANN J R. An algorithm for subgraph isomorphism [J]. Journal of the ACM， 1976， 23（1）： 31-42.

[4] CORDELLA L P， FOGGIA P. A （sub）graph isomorphism algorithm for matching large graphs [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2004， 26（10）： 1367-1372.

[5] HE H， SINGH A K. Graphs-at-a-time： query language and access methods for graph databases [C]// SIGMOD 2008： Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data. New York： ACM， 2008： 405-418.

[6] ZHANG S， LI S， YANG J. GADDI： distance index based subgraph matching in biological networks [C]// EDBT 2009：Proceedings of the 12th International Conference on Extending Database Technology： Advances in Database Technology. New York： ACM， 2009： 192-203.

[7] 張硕，李建中，高宏，等.一种多到一子图同构检测方法[J].软件学报，2010，21（3）：401-414.（ZHANG S， LI J Z， GAO H， et al. A multi-to-one subgraph isomorphism detection method [J]. Journal of Software， 2010， 21（3）： 401-414.）

[8] HAN W S， LEE J， LEE J H. TurboISO： towards ultrafast and robust subgraph isomorphism search in large graph databases [C]// ICMD 2013： Proceedings of the 2013 ACM SIGMOD International Conference on Management of Data. New York： ACM， 2013： 337-348.

[9] AFRATI F N， FOTAKIS D， ULLMAN J D. Enumerating subgraph instances using Map-Reduce [C]// ICDE2013： Proceedings of the 2013 IEEE International Conference on Data Engineering. Piscataway， NJ： IEEE， 2013： 62-73.

[10] PLANTENGA T. Inexact subgraph isomorphism in MapReduce [J]. Journal of Parallel & Distributed Computing， 2013， 73（2）： 164-175.

[11] SUN Z， WANG H Z， WANG H X， et al. Efficient subgraph matching on billion node graphs [J]. Proceedings of the VLDB Endowment， 2012， 5（9）： 788-799.

[12] 于静，刘燕兵，张宇，等.大规模图数据匹配技术综述[J].计算机研究与发展，2015，52（2）：391-409.（YU J， LIU Y B， ZHANG Y， et al. Survey on large-scale graph pattern matching [J]. Journal of Computer Research and Development， 2015， 52（2）： 391-409.）

[13] ZOU L， CHEN L， LU Y. Top-k subgraph matching query in a large graph[C]// PIKM 2007： Proceedings of the ACM first Ph. D. Workshop in Sixteenth ACM Conference on Information and Knowledge Management. New York： ACM， 2007： 139-146.

[14] NEUMANN T， WEIKUM G. The RDF-3X engine for scalable management of RDF data [J]. The VLDB Journal， 2010， 19（1）： 91-113.

[15] ATRE M， CHAOJI V， ZAKI M J， et al. Matrix “bit” loaded： a scalable lightweight join query processor for RDF data [C]// IW3C2： Proceedings of the 2010 International World Wide Web Conference Committee. New York： ACM， 2010： 41-50.

[16] HONG L， ZOU L， LIAN X， et al. Subgraph matching with set similarity in a large graph database [J]. IEEE Transactions on Knowledge and Data Engineering， 2015， 27（9）： 2507-2521.

[17] YAN X， YU P S， HAN J. Substructure similarity search in graph databases [C]// SIGMOD 2005： Proceedings of the 2005 ACM SIGMOD International Conference on Management of Data. New York： ACM， 2005： 766-777.

[18] Apache. Spark [EB/OL]. [2018-02-03]. http：//spark.apache.org.

[19] CHANG Z， ZOU L， LI F. Privacy preserving subgraph matching on large graphs in cloud [C]// ICMD2016： Proceedings of the 2016 International Conference on Management of Data. New York： ACM， 2016： 199-213.

[20] LESKOVEC J. SNAP [EB/OL]. [2018-03-03]. http：//snap.stanford.edu /snappy.