例谈“等时圆周”结论在动力学中的应用

徐美奖　王燕萍

摘要：对于比较几个质点在圆周或类似圆周情景中的运动时间的动力学问题，重点考查运动学和牛顿第二定律的基本规律.笔者通过对该类问题的研究，归纳出“等时圆周”结论，本文从两个方面分析“等时圆周”结论在动力学中的应用.

关键词：等时圆周;动力学;模型应用

1 基本模型及规律

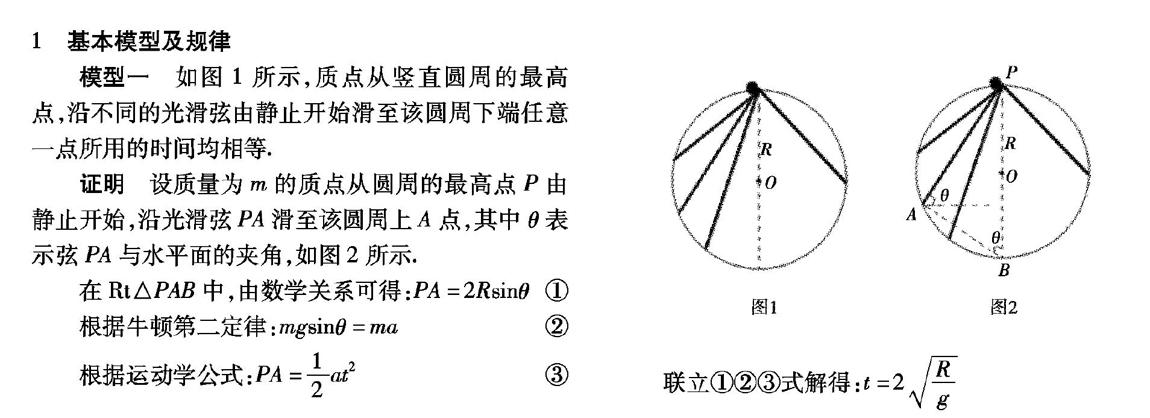
模型一如图1所示，质点从竖直圆周的最高点，沿不同的光滑弦由静止开始滑至该圆周下端任意一点所用的时间均相等.

证明设质量为m的质点从圆周的最高点P由静止开始，沿光滑弦PA滑至该圆周上A点，其中θ表示弦PA与水平面的夹角，如图2所示，

在Rt△PAB中，由数学关系可得：PA= 2Rsinθ①

根据牛顿第二定律：mgsinθ= ma

②

根据运动学公式：PA=1/2at²

③

可見运动时间t为定值，与到达圆周下端点的位置无关.

模型二如图3所示，质点从竖直圆周上端任意一点，沿不同的光滑弦由静止开始滑至该圆周的最低点所用的时间相等.

证明 设质量为m的质点从圆周上端任意一点A由静止开始，沿光滑弦AP滑至该圆周的最低点P，其中θ表示弦PA与水平面的夹角，如图4所示，

在Rt△PAB中，由数学关系可得：AP= 2Rsinθ①

2 典例赏析

例1如图5所示，位于竖直平面内的固定光滑圆环轨道与水平面相切于M点，与竖直墙相切于A点.竖直墙上另一点B与M的连线和水平面的夹角为600，C是圆环轨道的圆心.已知在同一时刻，a、b两球分别由A、B两点从静止开始沿光滑倾斜直轨道AM、BM运动到M点，而c球由C点自由下落到M点，则（ ）

A.a球最先到达M点

B.b球最先到达M点

C.c球最先到达M点

D.b球和c球都可能最先到达M点

点评 首先分析清楚各研究对象的运动情况是关键.其次，本题可巧妙地结合“等时圆周”的结论，进行定性分析，a球的运动时间等于一个“等时圆周”的时间，b球的运动时间大于一个“等时圆周”的时间，c球的运动时间小于一个“等时圆周”的时间，故c球最先到达M点.

例2 如图7所示，光滑细杆BC、DC和AC构成矩形ABCD的两邻边和对角线，AC：BC： DC =5：4：3，AC杆竖直.各杆上分别套有一小球a、b、d（可视为质点），a、b、d三小球的质量比为1：2：3.现让三小球同时从各杆的顶点由静止释放，不计空气阻力，则o、b、d三小球在各杆上滑行的时间之比为（ ）

A.1：1：l

B.5：4：3

C.5：8：9

D.1：2：3

解析 根据题设中所给的数学关系可知，该矩形的四个顶点位于以AC边长为直径的圆周上，如图8所示，故三个小球a、b、d的运动满足“模型二”中的情景，由“等时圆周”结论可知，它们的运动时间相等，所以选项A正确.

点评 利用数学知识解决物理问题是一项重要能力，本题要求学生能发现其中数学关系，并联系物理“等时圆周”模型，同时考查思维迁移能力，如果学生没有联想到用此模型的结论来求解，而是通过位移关系并运用动力学知识去计算小球的运动时间，将会花费较多时间.

例3 如图9所示，在倾角为θ的斜面上A点有一长为L= lOm的轻杆竖直放置.已知A点距斜面底端lOm，现从轻杆顶端B点处安装一滑索到斜面底端，不计摩擦阻力，取g=lOm/s²，则一可套在滑索上的小球从B点由静止开始滑到斜面底端的时间为（ ）

A.Is

B.√2s

C.2s

D.4s

点评 学生在求解本题时，分析小球沿滑索下滑做匀加速直线运动，可能会纠结如何表示其加速度和位移，而无法继续进行下去.如果我们巧妙地利用题于中的长度关系构建一个圆，就大大简化了过程分析，再直接利用“等时圆周”结论进行计算就显得非常简便.

点评 学生在解答本题容易错误套用“等时圆周”结论，而错选A选项.其实本题中三个小环下滑至a点并非圆周的最低点，因此本题应用动力学知识来求解.

变式应用2 如图12所示，在倾角为θ的斜面上方的A点处旋转一光滑的木板AB，B端刚好在斜面上.木板与竖直方向AC所成角度为a，一小物块自A端沿木板由静止滑下，要使物块滑到斜面的时间最短，则a角与θ角的大小关系应为（ ）

A.a=θ

B.a=θ/2

C.a=θ/3

D.a =20

解析 利用数学知识分析可知，要使物块从A点滑到斜面的时间最短，我们可以作一个合适的圆，这个圆的圆心在AC上，同时也经过A点.当这个圆恰好与斜面相切时，切点记为B，从A点到B点连线的方向就是木板AB应该放置的方向，如图13所示，再利用“等时圆周”结论可知，这样所用的时间最短.由数学关系知，∠COB=θ，∠OAB=∠OBA=a，根据三角形知识得θ=2a，即a=θ/2，故选项B正确.

点评 本题所求时间最短问题，学生不易想到对应何种情景，但是如果学生对“等时圆周”模型及规律非常熟悉，运用数学知识做出圆并与斜面相切其实就是我们要找的情景，这个问题就变得容易理解了.

参考文献：

[1]教育部课程教材研究中心所.普通高中课程标准实验教科书物理必修2教师用书[M].北京：人民教育出版社，2013.

[2]江四喜.高中物理经典名题精解精析[M].合肥：中国科学技术大学出版社，2018.

[3]钟小平.高中物理竞赛题典习题全解[M].杭州：浙江大学出版社，2012.

（收稿日期：2019 - 01 -15）