蚕丝纤维增强聚丙烯复合材料力学性能的试验优化设计
2019-07-31付胜明
付胜明
(衡水学院 数学与计算机学院,河北 衡水 053000)
1 引言
天然纤维增强复合材料由于具有减少对不可再生能源的依赖、降低污染物排放、降低温室气体排放、提高能量回收率和寿命终结生物降解性等环境效益而被广泛应用于许多领域[1].此外,用作增强体的复合材料中的天然纤维具有易加工性、低密度、轻质、非研磨性、低成本且危险性较小[2].复合材料性能受加工条件、基质与增强材料的配比与性能、基体与增强材料之间的粘结性、增强材料的形状、尺寸、取向及分布等因素的影响.这些特性可以通过适当选择合适的纤维、基质、添加剂和生产方法以便适用于各种类型的应用.
响应面方法(RSM)是一种用于开发、改进和优化过程的经验建模技术,用于评估一组受控实验因素与观测结果的关系[3].优化过程包括3个主要步骤:执行统计设计的实验,估计数学模型中的系数,预测响应/检查模型的适当性.在传统方法中,通过一次仅改变一个因子来优化这些因素.RSM能够同时确定许多因素的主效应和交互效应[4].
RSM优化在天然纤维素纤维增强复合材料的开发中得到了广泛的应用.文献[5]在压缩成型机中,羊毛纤维增强聚丙烯复合材料的制备过程中,当温度为176,时间为7 min,压力为35×105Pa时,获得了最佳机械性能.为实现旧报纸的再利用,研制了报纸纤维增强聚丙烯(NPF/PP)复合材料.研究了制备条件、添加剂和界面改性对复合材料力学性能的影响.提出了一种不经预处理直接将报纸纸涂敷在聚丙烯上的方法[6].制备了葛根纤维增强聚丙烯复合材料,测定了其力学性能和热性能.为提高葛根纤维与聚丙烯基体的粘附性,采用马来酸酐接枝聚丙烯(MAPP)作为增容剂.在MAPP质量分数为35%时,拉伸模量和拉伸强度均有持续改善.拉伸模量和拉伸强度分别提高了24%和54%[7].文献[8]采用Box-Behnken RSM实验设计研究了50%榴莲皮纤维含量、250~500纤维尺寸范围、0%马来酸酐聚丙烯含量对榴莲皮纤维增强聚丙烯复合材料冲击强度的影响.碱处理时间、纤维长度和纤维体积分数对棕榈纤维增强复合材料的拉伸强度影响很大[9].与注射成型温度和压力相比,亚麻纤维聚乙烯生物复合材料中的纤维含量对复合材料的拉伸和弯曲性能影响较大,复合材料的拉伸强度和弯曲强度随纤维含量的增加而增加.复合材料处理低于190具有较好的机械性能[10].
丝素是一种天然蛋白质纤维.纤维蛋白被各种昆虫和蜘蛛纺成纱线[11].家蚕茧丝由两种结构丝素丝组成,外覆胶状丝素蛋白.丝素由高比例的氨基酸组成,如丙氨酸、甘氨酸和丝氨酸.丝素蛋白是天然高分子聚合物,具有活性官能团,可生物降解[12].蚕丝纤维具有较高的强度、延展性和压缩性[13~16].这些性能使蚕丝纤维增强复合材料取代了合成纤维增强复合材料.在将蚕茧转化为丝素织物的过程中,在无梭织机的织机中会产生大量的切边废丝.这种原料仅用作生产粗纱.
在复合材料的开发中,废丝利用的有关于研究很少[17—19].目前还没有关于利用具有理想性能的RSM从废丝中提取再生蚕丝纤维制成复合板材的研究.因此,本研究旨在探索多响应优化工艺在蚕丝纤维增强聚丙烯复合材料生产中的应用,并研究工艺参数对复合材料力学性能的影响.
2 实验
2.1 材料
利用无梭织机织布废料回收的蚕丝纤维作为聚丙烯基质中的增强剂.通过除去现有的非丝素材料,即棉纱罗纱,清洁这种绸边硬废料.图1描绘了从无梭织机获得的丝绸布边废条的摄影图像.使用实验室模型硬质废弃物开放机,在最佳条件下,以553 r/min的舔入速度、354 r/min的汽缸速度、以及以11thou的舔入设定的进给辊,将这些丝质废弃物开放成纤维状.这种开放的丝绸布边废料被用作增强复合材料的制造,如图2所示.
以聚丙烯短纤维为粘结剂,采用Vadodara公司Zenith纤维为原料,制备的复合材料.这些纤维的物理性质在表1中给出.


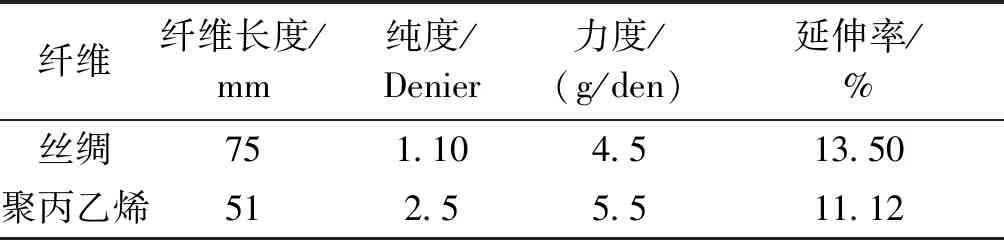
表1 纤维的物理性质
2.2 复合材料制造实验设计
采用三水平的三个因子的Box-Behnken设计(BBD)来设计实验.选择压缩成型机的加工条件如温度、时间和压力作为输入变量.输出变量为抗拉强度、抗弯强度和冲击强度.在表2中给出了三因子Box-Behnken实验设计.在选择了工艺变量及其范围之后,基于BBD建立了实验,整个设计包括17个处理,中心点重复5次,如表3所示.
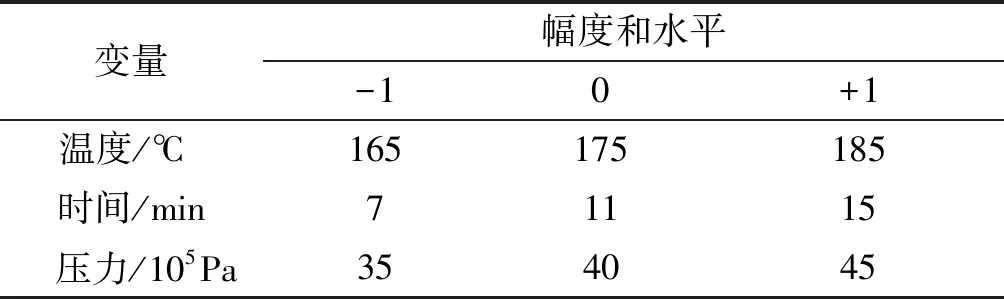
表2 Box-Behnken实验设计的实验范围和水平
2.3 复合材料制备
为了保持复合材料中增强纤维和聚丙烯纤维基质的理想重量,在实验室模型调配机中以质量比50∶50的配比(%)使用丝和聚丙烯纤维制备纤维共混物[20].将纤维共混物送入实验室模型梳理机以获得纤维网.梳理过程中,纤维混合物进一步展开,单个纤维被梳理为相对平行.将纤维共混物梳理4次,以增强织物的均匀性.在所得到的复合材料中叠加6个腹板以获得所需的厚度和重量.在压模成型机中应用叠合腹板.根据Box-Behnken实验设计,制备了17个复合样品.
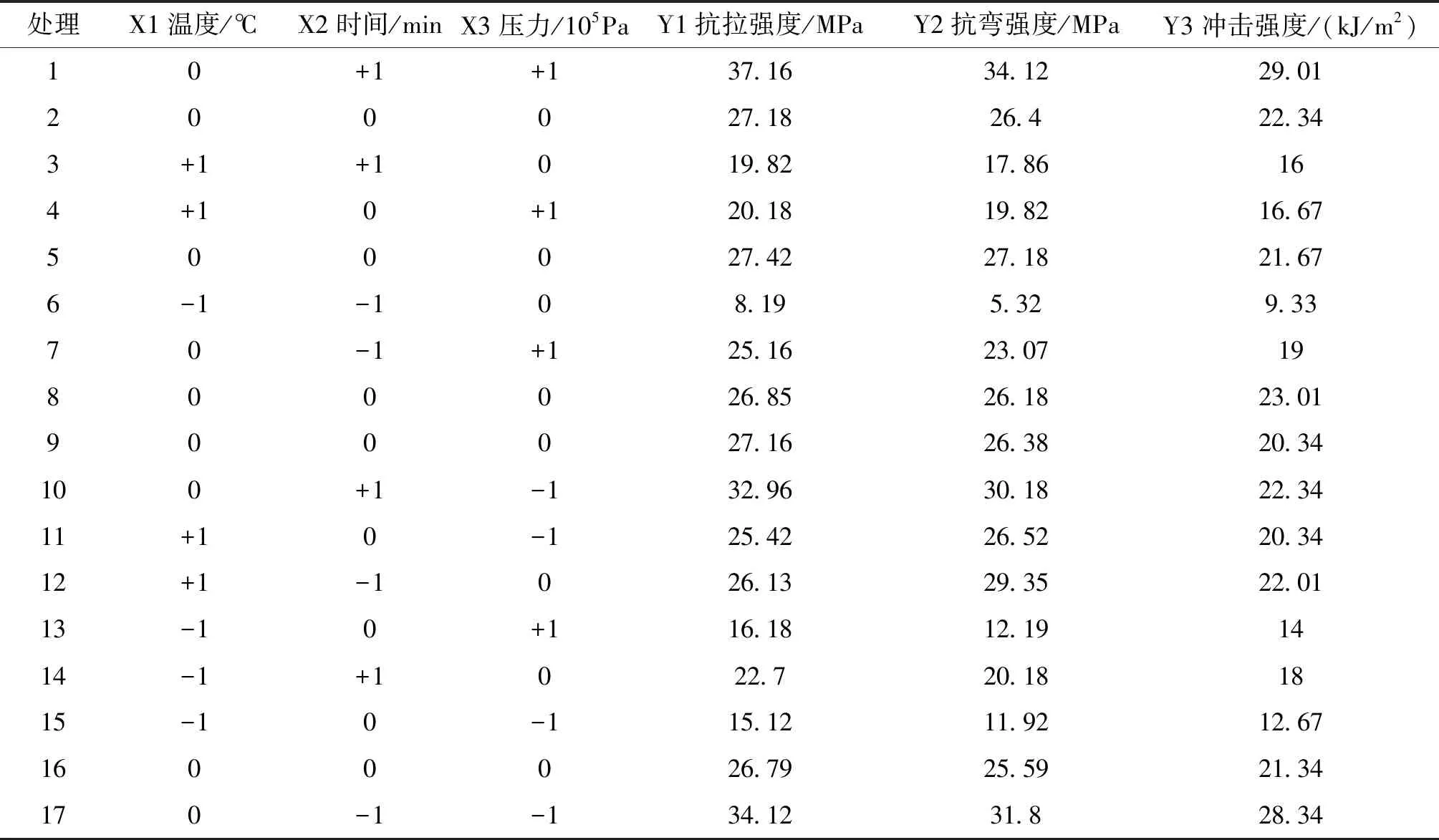
表3 Box-Behnken实验设计矩阵和实验响应.
2.4 复合测试复合材料的力学性能
在通用试验机(Instron拉伸试验机型号3345)上,根据ASTM D 638对蚕丝纤维增强聚丙烯复合材料进行了十字头速度50 mm/min的拉伸强度试验.采用ASTM D790-03三点弯曲法进行弯曲强度试验.在50 mm/min的十字头速度下对试样进行了测试.弯曲强度(FS)用下列方程确定
(1)
其中,P为最大负载(kgf),L为跨度(mm),b和t分别是样本的宽度(mm)和厚度(mm).采用摆锤式冲击强度试验机对ASTM D256进行了缺口冲击试验.标准试件尺寸为64×12.7×3 mm3,缺口下深度为10.2 mm.为每种类型的测试选择了精确的10个测试结果.
3 统计分析
统计分析使用minitab 17进行,对实验数据进行多元回归分析,用F检验评价回归系数的显著性,并在概率水平上验证F值的显著性(P<0.05).从一个包含线性项、平方项和交互项的二次模型开始建模.用、调整和预测误差平方和来检验模型的拟合性.通过方差分析(ANOVA)发现模型中的显著项.利用回归系数进行统计计算,由回归模型生成响应面等高线图.
3.1 响应面优化
利用数值优化技术-Derringer的期望函数法对响应进行了优化.该函数搜索通过满足设计中每个响应的要求,而联合优化一组响应的因子水平的组合.优化通过3个步骤完成,即,将每个响应Yi(i=1,2,…,m)转换为定义部分期望函数(di)的无量纲期望尺度,组合各个期望以获得全局期望函数(D),最后,识别最佳因子设置.可取函数的尺度介于0(完全不希望的响应)和1(完全期望的响应)之间.通过指定目标,即最小化、最大化或目标响应,以及每一个响应的边界,获得每个响应的个体期望值(D).分配了一个权重因子用于解释了每个响应的可取性函数的形状.权重必须在0.1到10之间,权重越大相应的响应变量越重要的.在本文研究中,所有响应变量权重系数都选择为1.
3.2 方差分析结果与回归模型
通过试验确定了最佳工艺条件,研究了工艺参数对丝素增强聚丙烯复合材料力学性能的影响.响应拉伸强度、弯曲强度和冲击强度的实验结果在表3中列出.在表4至6中给出了抗拉强度、抗弯强度和冲击强度的方差分析结果.R2度量因变量的变异中可由自变量解释部分所占的比例,以此来判断统计模型的解释力.较高的决定系数证实了模型的适用性和预测值的正确性.得到的响应强度、弯曲强度和冲击强度的R2值分别为0.998 5、0.993 5和0.989 5,保证了模型与实验数据的良好拟合.调整后的R2值分别为0.996 5、0.985 1和0.976 0.预测的R2值分别为0.980 5、0.915 1和0.974 7.发现拉伸强度、弯曲强度和冲击强度与工艺参数之间的关系很好地解释了因变量的变异中可由自变量解释部分所占的比例非常高,说明统计模型的解释力非常好.调整后的R2和预测的R2的值表明观察值和预测值有很高的决定系数.
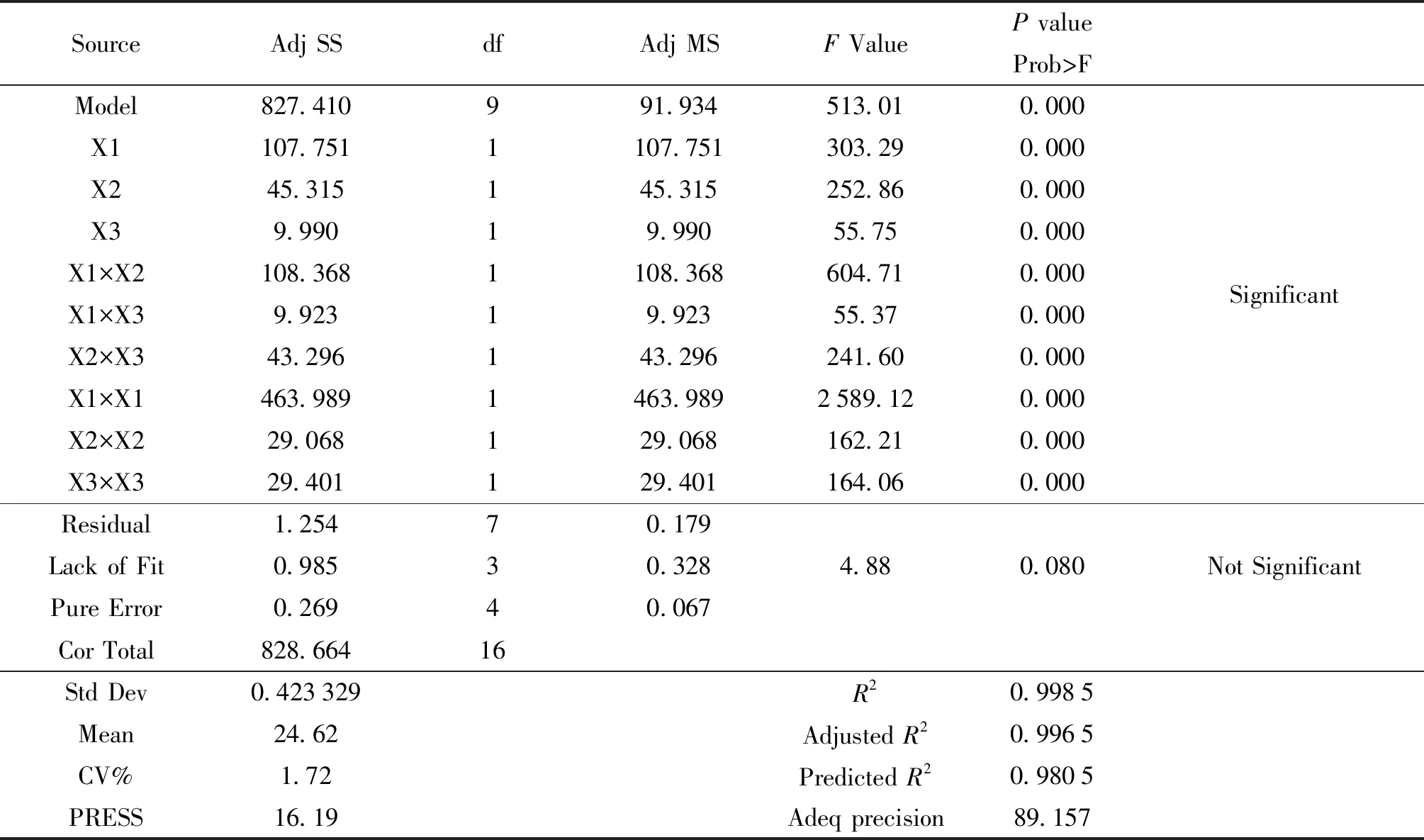
表4 二次模型的统计参数与方差分析表(抗拉强度)

表5 二次模型的统计参数与方差分析表(响应:抗弯强度)

表6 二次模型的统计参数与方差分析表(响应:冲击强度强度)
二次回归模型的方差分析中,Fisher的F-Test(抗拉强度的F值为513.01、抗弯强度的F值为118.36和冲击强度的F值为73.27)和非常低的概率值(p=0.000)表明,该模型具有较高的显著性.获得3个响应的CV%为1.72、4.08和3.99.CV%的值表示实验进行的精确度.低的CV%值暗示了实验的高可靠性[21-22].本研究所获得的响应的抗拉强度、抗弯强度和冲击强度的最佳值分别为36.978 1 MPa、37.111 5 MPa和30.469 kJ/m2.由BBD获得的实验结果之间的经验关系用二阶多项式方程表示,并且针对编码因子得出的方程在表7中给出.

表7 蚕丝纤维增强聚丙烯复合材料力学性能的模型方程
3.3 模型的拟合性
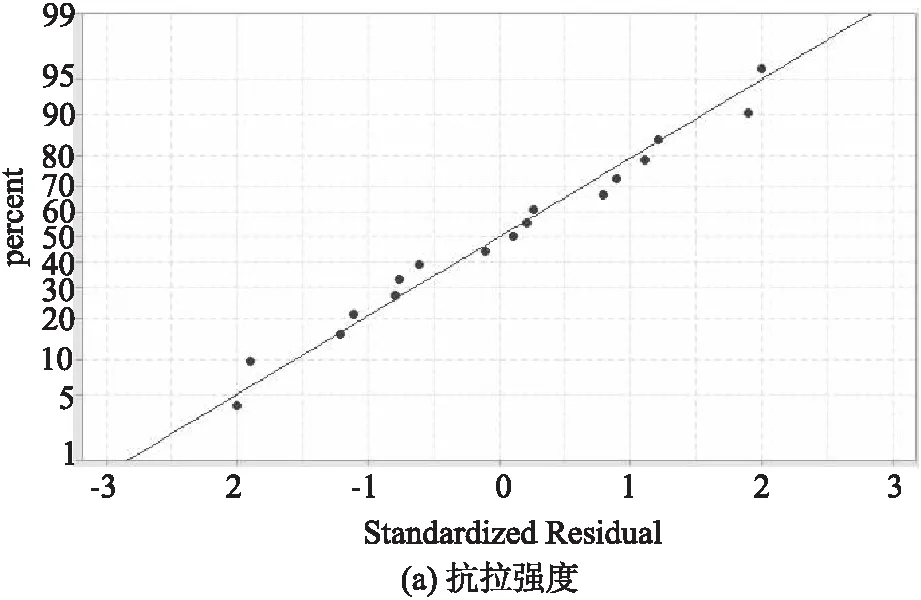
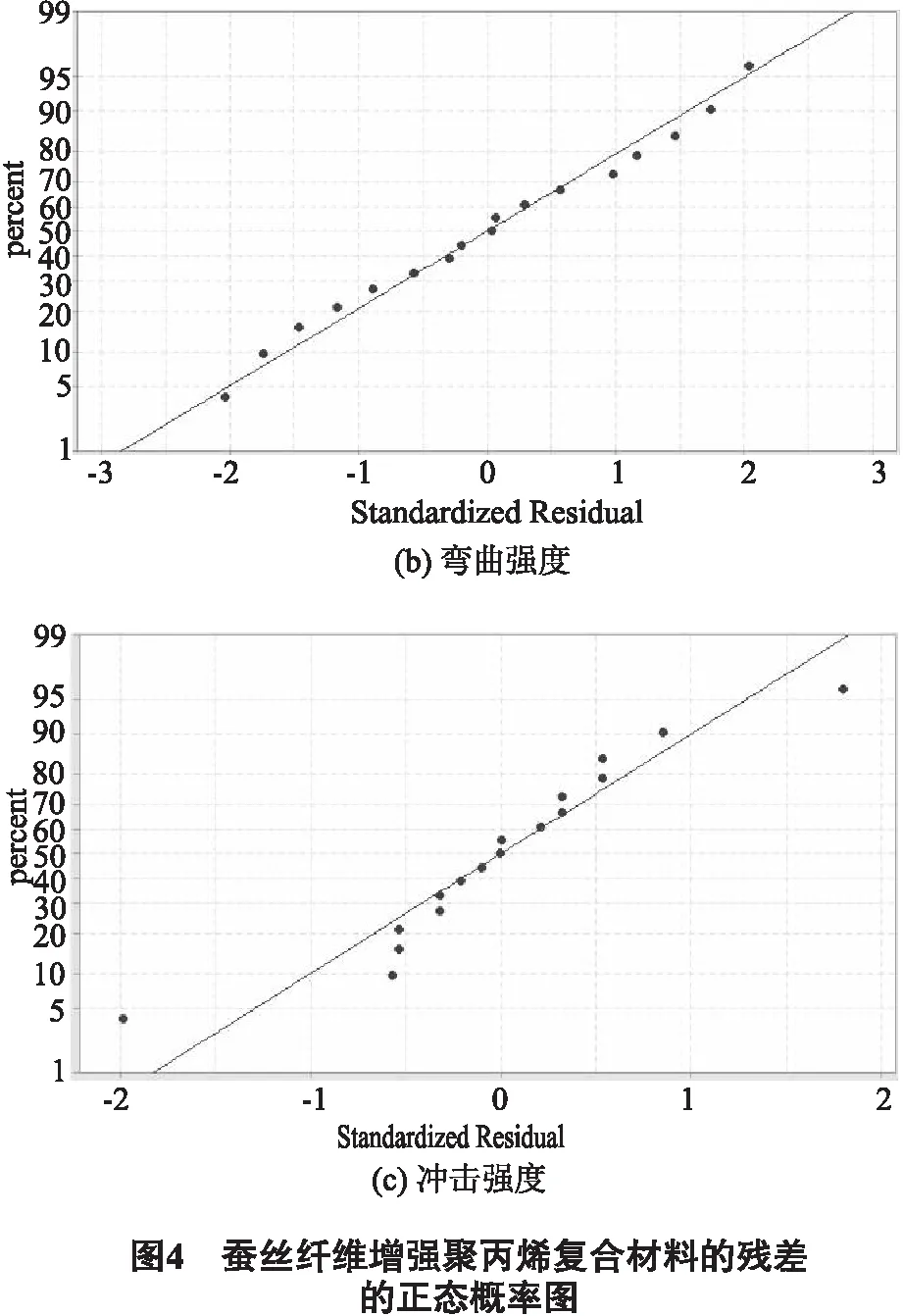
构造接近实际值的拟合模型,满意的模型与诊断曲线(如预测值与实验值)相吻合.图还显示了预测值与实验值之间的关系.图3显示了反映拉伸强度、弯曲强度和冲击强度的诊断图.该图上的数据点倾斜地接近直线,这表明实际数据和从模型中获得的预测数据之间有足够的一致性.结果表明,本文建立的模型能较好地确定蚕丝纤维增强聚丙烯复合材料的制备工艺条件.通过分析数据,检验了残差的正态性.图4所示的正态概率图描述了残差的正态分布.残差提供了响应的观测值与理论模型下拟合的值之间的差异.小残值表明模型预测是准确的[23].在图4中,数据点相当接近直线,可以得出数据是正态分布的.

3.4 操作变量间的相互作用
生成二维等高线图用于研究变量间的相互效应.通过变量在实验范围内变化来生成绘图.(a)时间与温度对响应抗拉强度的相互作用关系的等值线图、(b)压力与温度对响应抗拉强度的相互作用关系的等值线图、(c)压力与时间对响应抗拉强度的相互作用关系的等值线图,如图5(a)至(c)所示.图5(a)和(b)显示直到中等温度水平,可变温度分别与变量时间和压力的近似线性关系,而在较高的温度下,变成曲线或非线性关系.图5(c)中的变量时间和压力在两个变量的各水平都显示出非线性关系.可以看出拉伸强度随温度的升高先上升后下降.复合材料的抗拉强度下降是由于蚕丝纤维的热降解.文献[24]已报道了黄麻纤维/聚乳酸复合材料的抗拉强度有类似的结果,还指出抗拉强度随着成型时间的增加而增加.
图6(a)至(c)分别显示了(a)时间和温度、(b)压力和温度、(c)压力和时间对蚕丝纤维增强聚丙烯复合材料抗弯强度的相互作用的等高线图.图6(a)和(b)显示直到中等温度水平,可变温度分别与变量时间和压力的近似线性关系,而在较高的温度下,变成曲线或非线性关系.随着温度的升高,抗弯强度开始增加,随后,抗弯强度下降.图6(c)显示变量时间和压力具有非线性关系.抗弯强度随成型时间的增加而增加.基质和纤维之间的良好润湿致使在较高模塑时间内纤维在基质中的更好浸渍[25].随着成型压力的增加,抗弯强度降低.这是由于在低成型压力下部件具有良好的部件固结性[26].在179 ℃、7 min和35×105Pa力下获得了37.12MPa的最大弯曲强度.

图7(a)至(c)分别描绘了(a)时间和温度、(b)压力和温度以及(c)压力和时间对蚕丝纤维增强聚丙烯复合材料冲击强度的相互作用的等高线图.在中等温度以下,温度和时间、压力之间的相互效应呈线性关系,正如拉伸强度和弯曲强度.在较高温度下,这变成曲线或非线性关系,如图7(a)和(b)所示.观察到冲击强度随着温度的升高先增加后降低.在图7(c)中,变量时间和压力在所有水平上都呈非线性关系.冲击强度随成型时间的增加而降低.随着成型压力的增加,冲击强度降低.由于树脂的熔融性较好,纤维与树脂之间的界面在增加成型时间时可能较好,并且施加高压会使复合材料更加坚硬,从而降低冲击强度.在179 ℃、7 min和35×105Pa压力下获得了约30.47 kJ/m2的最佳冲击强度.

3.5 最佳条件的选择
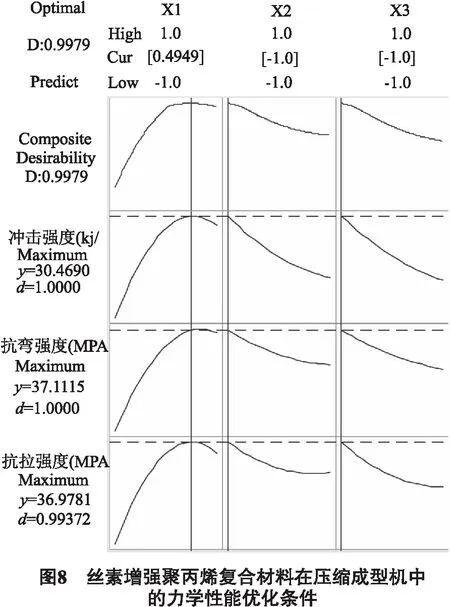
确定了蚕丝纤维增强聚丙烯复合材料力学性能的最佳条件,以获得最大拉伸强度、抗弯强度和冲击强度.本研究中建立的二阶多项式模型用于每个响应,以获得特定的最佳条件.Derringer期望函数法用于多个反应的优化.在177.5 ℃的温度、7 min的时间和35 bar的压力下,获得了36.978 1 MPa、37.111 5 MPa和30.469 kJ/m2的最佳拉伸强度、弯曲强度和冲击强度.图8描绘了在压缩成型机中蚕丝纤维增强聚丙烯复合材料力学性能的优化条件.
4 结论
采用基于RSM的Box-Behnken实验设计方法,对蚕丝纤维增强聚丙烯复合材料压缩成型工艺参数进行了优化.基于二阶多项式方程,发现温度、时间和压力三个因素对蚕丝纤维增强聚丙烯复合材料有显著影响.确定了其最大抗拉强度、抗弯强度和冲击强度的最佳工艺参数为:温度1 775 ℃、时间7 min和35×105Pa.目前还没有关于利用具有理想性能的RSM从废丝中提取再生蚕丝纤维制成复合板材的研究.因此,本研究将多响应优化工艺应用与蚕丝纤维增强聚丙烯复合材料生产中,并研究工艺参数对复合材料力学性能的影响,求得了较好的效果.
