含多种分布式电源的配电网概率无功优化
2019-07-31文天舒董跃哲
文天舒,马 平,董跃哲
(青岛大学 电气工程学院,山东 青岛 266071)
无功优化通过对系统中的控制变量进行优化配置,可以减小系统网络有功损耗,提高电能质量.配电网无功优化本质上是多目标、多约束、多变量的电力系统规划问题[1],众多学者对该问题进行了研究.文献[2]以有系统功网损最小为目标,建立了配电网无功优化模型,采用差分进化入侵野草算法求解目标函数.文献[3]以系统费用最小为目标,提出一种分合群粒子群算法求解模型.文献[4]则把电压和分布式电源无功出力越限罚函数引入无功优化模型中,采用简化改进粒子群算法求解模型.
在传统配电网中,负荷的随机性是影响无功优化结果的主要因素.随着电力工业的发展,以风电、光伏等为代表的分布式电源(distributed generator,DG)在配电网中的渗透率不断提高[5],导致系统中的不确定因素进一步增加,传统确定性条件下的无功优化方法[2-4]已不能满足实际的需要.因此,研究考虑不确定因素的配电网无功优化问题具有实际的意义.文献[6]利用场景分析法来描述风机出力的随机性,将风机出力分为三种确定的场景,对每种场景进行确定性的无功优化.文献[7]建立了考虑光伏出力随机性的无功优化模型,采用Gaussian-Hermite积分法进行概率潮流计算.文献[8]建立了同时考虑光伏出力及负荷随机性的无功优化模型,采用一种基于全概率公式的概率潮流方法进行计算.文献[9]则采用蒙特卡洛模拟法得到风电机组的输出功率,将不确定性问题转化为单场景确定性潮流问题.
1 分布式电源及负荷的概率模型
1.1 风力发电概率模型
风机的输出功率通常是不可控的随机变量,其随机性主要取决于风速的随机性,与风机的安装地点以及当地天气有关.大量研究表明风速服从Weibull分布[8-9],其概率密度函数为:
(1)
其中,k、c为Weibull分布的2个参数.
风机的有功输出Pw与风速v的关系曲线如图1所示:
由图1可得风机有功输出的分段函数:
(2)
其中,Pr为风机的额定有功功率;vi、vr、vo分别为切入风速、额定风速和切出风速.
目前风力发电多采用恒速异步发电机,并网运行时需要吸收电网的无功功率,假设风机为恒功率因数控制,则风机的无功输出可由下式表示:
Qw=-Pwtan(arccosφw),
(3)
其中,φw为风电机组的功率因数角;Qw为风机输出的无功功率.
1.2 光伏发电概率模型
光伏发电的输出功率与太阳光照强度密切相关,太阳光照强度近似服从Beta分布,因而光伏发电机组的输出功率也呈Beta分布[12-13],其概率密度函数为:
(4)
QPV=PPVtan(φpv) ,
(5)
其中,PPV和QPV分别为光伏发电机组的有功输出和无功输出;PPV max为最大有功输出;a和b为形状参数;φpv为光伏发电机组的功率因数角;Γ为Gamma函数.
1.3 负荷概率模型
系统中负荷通常具有一定的随机性,一般采用正态分布来描述[9],假设负荷功率因素保持不变,则概率密度函数为:
(6)
QL=PLtan(φL),
(7)
其中,PL和QL分别为负荷的有功功率和无功功率;μL和σL分别为负荷有功的期望和标准差;φL为负荷的功率因数角.
2 配电网概率无功优化模型
DG和负荷的接入改变了配电网的潮流分布,为无功优化带来不确定性.为充分考虑上述不确定因素的影响,将三点估计法引入无功优化模型进行优化求解,得到确定的控制变量最优解以及相应的状态变量统计矩.
2.1 目标函数
为兼顾配电网运行的经济性和安全性,以系统有功网损期望值和节点电压偏移期望值最小为目标函数,如式(7)所示:
(8)
其中,E(Ploss)为有功网损期望值;E(ΔU)为电压偏移期望值.
(9)
其中,Ui、Uj分别为节点i、j的电压;gij为线路i-j的电导;δij为节点i和j电压的相位差;m为系统支路总数;UN为额定电压;n为系统节点总数.
(10)
其中,F1min、F2min分别为有功网损和电压偏移的理想值,F1max、F2max分别为优化前有功网损和电压偏移的初始值.通过上述归一化处理就可以让F1′与F2′直接相加,同时通过控制权重系数来体现偏好的选择,并引入电压越限罚函数,则最终目标函数为:
(11)
(12)
其中,α1、α2为权重系数反映了优化运行时对配电网经济性和安全性的偏好程度;同时要求满足α1+α2=1,本文取α1=0.8、α2=0.2;λ为罚系数;Ui为节点i的电压,Uimin、Uimax为节点i的电压上下限.
2.2 约束条件
等式约束:
(13)
其中,Pi、Qi分别为节点i注入的有功功率和无功功率;n为系统节点总数;θ为节点i、j之间的节点电压相角差;Gij和Bij分别为i-j支路的电导和电纳.
不等式约束:
(14)
其中,Qci电容器在节点i的补偿容量;Qci,max和Qci,min分别为节点i安装的电容器容量上下限;T为有载调压变压器挡位;Tmin和Tmax分别为有载调压变压器档位上下限.
目前分区的方法很多,常用的主要有经验定性法、指标法、类型法、重叠法、聚类分析法等。本研究采用定性分析与定量分析相结合的方法,前者选用经验定型法,后者采用聚类分析法。
3 模型的求解
3.1 三点估计法
在利用三点估计法[10-12]进行概率潮流计算时,只需根据历史数据求出各随机变量的期望、标准差、偏度和峰度,就可以通过三点估计法得到输出随机变量的概率数字特征(期望和标准差).该方法计算量小精度高,能有效处理电力系统中出现的不确定性问题,在电力问题中已得到了广泛的运用.
设F=f(x1,x2,…,xn)是由n维随机变量(x1,x2,…,xn)构成的函数,xk(k=1,2,…,n)为n维随机变量中的任意一个,在xk上取三个采样值,每个采样值对应的位置系数的表达式为:
(15)
其中,ξk,i为随机变量xk的位置系数,λk,3和λk,4分别为xk的偏度和峰度系数.
将xk的期望值、标准差和位置系数代入下式,可得xk的3个采样值:
xk,i=μk+ξk,iσk,(k=1,2,…,n,i=1,2,3),
(16)
其中,μk和σk分别为xk的期望值和标准差.
每一个采样值所对应的权重系数pk,i为:
(17)
由n个随机变量的3n个采样值,通过确定的函数关系F=f(x1,x2,…,xn),对F进行2n+1次估计,可得F在所有估计点处的值f,然后求出f的λ次方与pk的内积之和,就得到F的各阶矩估计值:
(18)
其中,当λ=1时,E(F)为F的期望值;当λ=2时,可得F的标准差.
(19)
3.2 改进的粒子群算法
粒子群算法(PSO)是一种基于群体的人工智能算法[14].传统PSO算法易陷入局部最优,导致优化效果不理想.因此本文通过以下3个方面来进行改进:
1)惯性权重系数ω描述上一代速度对当前代速度的影响,对ω进行控制可以很好的增加粒子的搜索能力,本文选择指数递减惯性权重策略[4],如式(20)所示:
(20)
其中,ω1、ω2分别为0.9和0.4;可调参数m=10;t为迭代次数;Tmax为最大迭代次数.
2)在算法初期赋予较大的c1和较小的c2,使c1>c2,以提高粒子初期的全局搜索能力,算法后期赋予较小的c1和较大的c2,使c1 (21) 其中,下标“max”和“min”分别为加速因子的上、下限;k为当前代数. 3)将PSO中的个体粒子最优值由所有粒子最优值的平均值来代替[15].增加粒子的群体性,减少粒子的个体效应,可以较好地避免算法陷入局部最优极值. 综合上述三点,IPSO算法的速度、位置更新公式为: (22) (23) 其中,r1、r2为0~1间相互独立的随机数;ω为惯性权重;c1、c2为加速因子;vti、xti分别为第i个粒子的速度和位置;ptid、ptgd分别为粒子的个体极值和全局极值. 1) 输入配电网原始线路参数,IPSO算法参数,在控制变量约束范围内,随机生成所有粒子的初始值,取迭代次数t=0. 2) 利用三点估计法对全体粒子进行初始概率潮流计算,得到有功网损和电压偏移,进而计算目标函数式(11)的值,并进行评估,确定局部最优值和全局最优值,记录fmin和favg. 3) 更新迭代次数t=t+1,先根据式(20)、(21)更新粒子的权重系数和加速因子,再根据式(22)、(23)更新粒子的速度、位置. 4) 进行概率潮流计算和各粒子目标函数值计算,并进行评估,确定局部最优值和全局最优值,更新并记录fmin和favg. 5) 重复步骤3)和4),直到达到最大迭代次数,并输出最优粒子和目标函数值. 本文通过matlab软件进行编程,对改进的IEEE33节点辐射型配电网进行仿真测试,如图2所示,系统原始数据参见文献[16]. 系统基准电压为12.66 kV,节点电压允许范围0.95~1.05 pu(1pu=12.66 kv);系统总有功负荷为3715 kW,总无功负荷为2 300 kW,负荷功率因数恒定为其基础负荷的功率因数,各节点负荷服从以测试系统的基础负荷为期望值,期望值的5%为标准差的正态分布;在0~1节点间加入有载调压变压器,变压器档位为8档,调节范围±4×1.25%;在节点18和节点33处接入光伏系统额定容量均为600 kW,Beta分布形状参数a和b分别为0.58和1.51;在节点10和节点22处接入风电系统,额定容量均为400 kW,Weibull模型参数k和c分别为8.5和2.0,切入风速、额定风速、切出风速分别为3、11和30 m/s;风-光系统的功率因数保持恒定,功率因数均取0.98(滞后);节点6、15、29为无功补偿装置的安装位置,每个节点共安装10组可投切电容器组,每组容量为100 kvar;IPSO算法参数设置:种群数为50,最大迭代次数为100,c1min=c2min=0.5,c1max=c2max=2.5. 为验证本文所提模型的可行性,分别对仅接入波动负荷不接入DG(方法1)、同时接入DG和波动负荷(方法2)的IEEE33节点系统进行测试.优化前后系统控制变量参数如表1所示,优化结果如表2所示,两种方法优化前后系统节点电压如图3、4所示. 表1 优化前后系统控制变量参数 表2 系统优化结果比较 根据上述优化结果可知:系统接入DG后,网损下降至155.63 kW,减少20.48%,电压偏移下降至1.439 2 pu,减少11.15%,可见即使在优化前,系统网损和电压偏移都低于未接入DG的情况,说明DG的接入有利于提高系统的经济性和安全性;对于方法1,无功优化后系统网损下降至119.35 kW,减少39.02%,电压偏移下降至0.844 1 pu,减少47.87%,说明变压器和无功补偿装置的运用可有效降低系统网损和电压偏移;对于方法2,无功优化后系统网损和电压偏移进一步下降,分别减少51.10%和52.42%,且投入的无功补偿设备容量明显低于方法1,降低了配电网的投资成本.综上所述,本文所建模型和算法能有效降低系统有功网损和电压偏移,提高系统运行的经济性和安全性. 为验证三点估计法的有效性,将其与多种概率潮流计算方法进行对比测试.在接入DG和波动负荷的IEEE33节点系统中,将三点估计法、蒙特卡洛模拟法、场景分析法分别进行测试,测试结果如表3所示.可以看出,三种计算方法的误差处在一定的范围之内,说明3种计算方法对不确定性的处理均具有一定的有效性和适应性.场景分析法计算误差最大,计算时间介于前两种方法之间,三点估计法与蒙特卡洛模拟法的测试结果最为接近,但计算时间大幅缩短.由此说明三点估计法适合模拟随机变量的随机变化,能有效处理含多种不确定因素的配电网概率无功优化问题. 表3 算法测试结果比较 为验证IPSO算法的有效性,作为对比将其与传统PSO算法进行比较.PSO算法参数设置:种群数为50,最大迭代次数为100,ω=0.8,c1=c2=2.分别对接入分布式电源和波动负荷的IEEE33节点系统进行测试,2种算法收敛特性曲线如图5所示. IPSO算法相较于传统PSO算法降低系统网损和电压偏移的能力更优秀,说明将PSO中的个体粒子最优值,由所有粒子最优值的平均值来代替能够有效克服早熟收敛的问题,使寻优值更精确.其次IPSO算法在第22次迭代时就已接近最小值,而PSO在第35次迭代时才接近最优,说明对惯性权重和加速因子进行控制后,算法搜索能力得到增强,从而收敛速度更快. 本文基于多种分布式电源出力和负荷的随机性,建立了考虑多重不确定因素的配电网概率无功优化模型,利用能够处理不确定因素的三点估计法和改进粒子群算法进行求解.在改进的IEEE33节点系统上进行仿真测试,结果表明:三点估计法可准确得到输出随机变量的概率数字特征,且计算速度快;IPSO算法收敛速度快,寻优值更精确,具有较好优化性能和实用性能;所提无功优化方法在不确定条件下能有效减少系统有功网损和电压偏移,从而保证了系统的安全经济运行.3.3 计算流程
4 算例分析
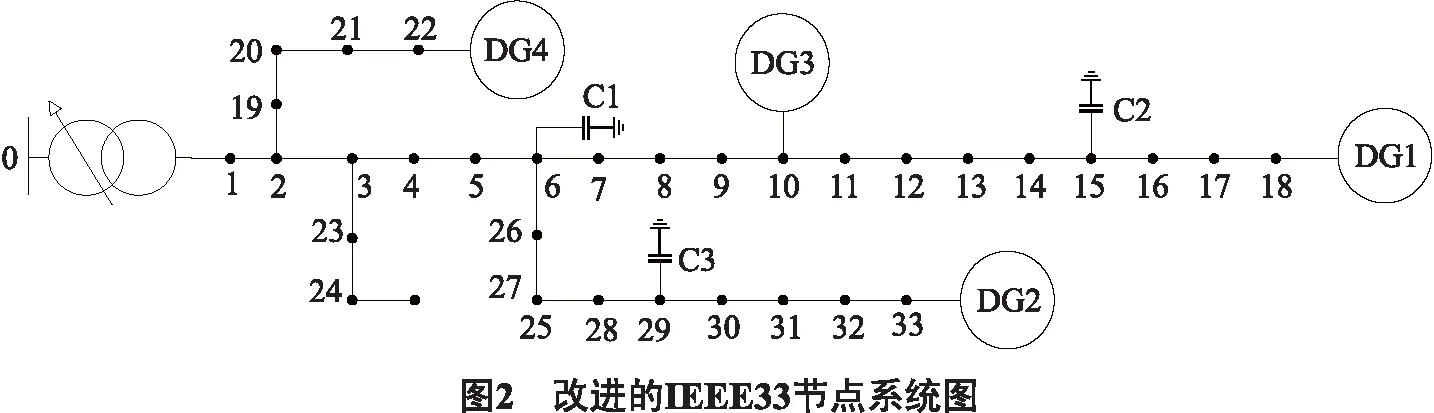
4.1 优化效果测试



4.2 不同概率潮流计算方法对比分析

4.3 算法性能测试
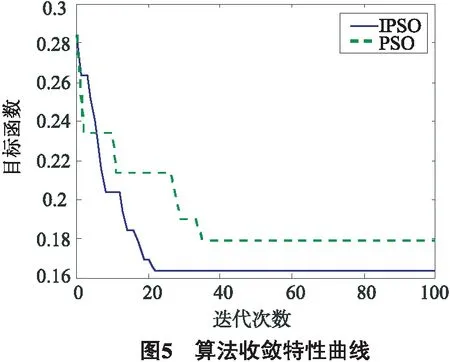
5 结语
