中国土地轮耕发展的数学模型研究

吴万勤，陈 娇，谭 昊，聂俊宇

(云南民族大学 数学与计算机科学学院，云南 昆明 650500)

0 引言

2016年开始，我国推行土地轮耕试点，轮作休耕就是要压减库存压力大的玉米和稻谷，优化资源配置，调整种植结构，减少无效供给，增加有效供给.轮作主要是实行玉米大豆轮作，发挥大豆根瘤固氮、养地培肥作用，实现种地养地结合，农业可持续发展.休耕就是减少耕地水资源利用，使耕地得到休养生息，同时加以治理.我国是一个人口大国，粮食安全是国之根本，轮耕必须在粮食安全范围之内，要形成耕地轮作休耕制度，国家财政投入是重要的支撑.土地轮耕对粮食安全有没有影响？2017年轮耕土地1 200万亩，其中轮作1 000万亩，休耕200万亩，影响粮食产量近80亿斤，相当于整个粮食年产量的0.6%.数据显示，2016年中央财政安排了14.36亿元，试点面积616万亩；2017年安排了25.6亿元，试点面积1 200万亩；2018 年拟安排约50亿元，试点面积2 400万亩.关于我国目前农村现状和粮食分布状况、土地轮耕发展方向对未来农业发展的影响大小以及预测我国未来主要粮食产量和土地轮耕面积等问题，我们运用样本回归模型[1]、灰色预测模型等方法来进行研究.

灰色预测模型一般是指GM(1,1)模型及其扩展形式，主要包括GM(1,1)模型、DGM模型和灰色Verhuls模型.GM(1,1)模型是灰色预测理论的基础，其应用价值已经被人们所认同并已应用在社会的各个领域中.研究数据光滑度是很多学者选择提高模型精度的方法，陈捷涛等[2]提出了用几种典型的函数变换方法来提高原始数据序列的光滑度，从而使模型获得了较高的预测精度；罗党[3]应用实际曲线在区间上的面积作为背景值，重构了背景值的计算公式；何海[4]等指出了GM(1,1)的预测公式初值选取存在的缺陷，给出了几种不同的初值选取方法 ；周伟[5]经过对GM(1)模型差分方程研究得出了差分GM(,1)模型以及还原时间响应函数，从而推导出基于级比优化的广义GM(1,1)预测模型；谢乃明[6]从GM(1,1)模型的离散形式到白化形式的转变，以及GM(1,1)模型预测稳定性问题为出发点，提出了能完全拟合指数序列的离散GM(1,1)预测模型.

对中国土地轮耕对粮食安全影响的问题，从统计的角度分析并建立数学模型求解.一是通过2016年至2018年土地轮耕数据分析，建立样本回归模型，以此来预测总体回归模型，从而计算轮耕影响粮食产量达到5%时，中央财政预计需要安排的专项补贴资金；二是对于影响因素，建立了灰色预测模型，并建立常微分方程，来预测在国家粮食安全保障的基础之下，2023年后我国可轮耕土地面积；三是兼顾国家财政的收入和投入，拟合财政收入与轮耕面积的曲线图，从而预测我国5年后每年的土地轮耕面积，以及相应的国家财政投入.

1 土地轮耕数学模型

1.1 有关条件

1) 假设搜索的数据、资料具有代表性，且真实可靠；

2) 假设粮食总产量主要受问题中七个因素的影响，其他因素的影响忽略不计；

3) 假设在预测过程中不考虑自然因素对粮食产量的影响；

4) 假设数据统计的年限内没有特大自然灾害；

5) 假设土地轮耕发展的各因素限定,且不会互相影响.

1.2 符号说明

A(t)表示粮食的需求量，B(t)表示粮食的消费量，Y(t)表示粮食的生产量，F表示由地少缺水、城市化建设引起的粮食需求量，I表示由农村贫困人口及2亿粮食不能自给的因素引起的需求量，L表示生产水平的变化率与需求量和生产水平差的比例系数，k表示消费系数，a表示常数，s表示积累系数，m表示常数，α表示式子中的代表量，β表示式子中的代表量.

1.3 模型的建立

对于建立样本回归模型.现实问题的研究中，往往难以掌握研究对象的全部资料，因此，总体回归模型是未知的，从而在回归分析中，需要通过样本资料来估计总体模型的参数.根据样本数据建立的回归模型为样本回归模型，一般表述如下：

建立灰色预测模型.灰色预测是对既含有已知信息又含有不确定信息的系统进行预则，就是对在一定范围内变化的、与时间有关的灰色过程进行预测.它通过鉴别系统因素之间发展趋势的相异程度，即进行关联分析，并对原始数据进行生成处理来寻找系统变动的规律，生成有较强规律性的数据序列，然后建立相应的微分方程模型，从而预测事物未来发展趋势的状况.灰色预测法用等时距观测到的反映预测对象特征的一系列数量值构造灰色预测模型，预测未来某一时刻的特征量，或达到某一特征量的时间.其模型建立如下：

设原始数据为：

x(0)=x(0)(1),x(0)(2),…,x(0)(n);

其一次累加生成数列为：

x(1)=x(1)(1)，x(1)(2)，…,x(1)(n)；

定义x(1)的灰导数为：

d(k)=x(0)(k)=x(1)(k)-x(1)(k-1).

令z(1)为数列的邻值生成数列，即：

z(1)(k)=αx(1)+(1-α)x(1)(k-1).

于是定义灰色预测模型的常微分方程为：

d(k)=αz(1)(k)=b,

x(0)(k)+αz(1)(k)=b.

将时刻表k=2,3,…,n代入有

引入矩阵向量：

所以灰色预测模型可表示为：Y=Bu.

2 数学模型的求解和分析

2.1 样本回归模型的求解

2017年影响粮食产量近80亿斤，相当于整个粮食年产量的0.6%，由这两个数据可以计算出粮食年产量为13 333.33亿斤，当轮耕影响粮食产量达到5%时，则可以得到影响粮食产量为666.67亿斤.设轮耕面积为x，中央政府补贴资金为y.

根据2016—2017年国家统计数据，以及上述计算出的数据，以轮耕面积为x轴,中央政府补贴资金为y轴，得到如下散点图：

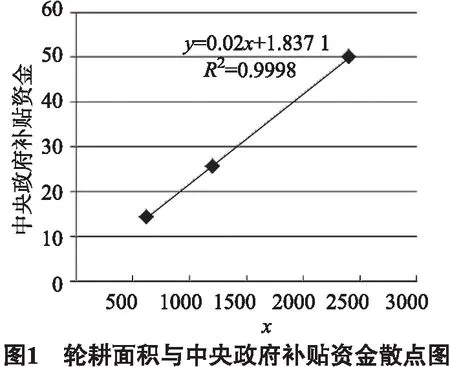
由图1中得出样本回归模型的表达式为：

y= 0.02x+ 1.837 1.

(1)

由轮耕面积和轮耕影响的粮食产量得到方程式为：

666.67=0.137x-84.384.

(2)

将(2)中计算出的x值带入(1)中的样本回归模型的表达式中得到，如果轮耕影响粮食产量达到5%时，中央财政预计需要安排的专项补贴资金111.479 5亿元.

2.2 灰色预测模型的求解

土地轮耕的影响因素有国家财政收入、国家人口数量、人均粮食需求、工业粮食需求、粮食产量、耕地面积变化、天气气候等，类比国民经济数学模型，列出求解粮食总产量的常微分方程：

A(t)=B(t)+I+F.

B=kYdY/dt=L(A-Y)，积累系数

A=(L-s)Y+I+F,即

dY/dt+LsY=L(I+F),

Y″+LsY′=LI′,

Y″+(Ls-Lma)Y′+LmI=0，

I=Y′/L+sY-F，

Y″+(Ls+m-Lma)Y′+sLmY=LmF.

在此引入代表量

α=Ls+m-Lma，

β=sLm，

Y″+αY′+βY′=LmF.

这是一个关于粮食生产总量的二阶常系数微分方程，其α、β、L、m、F及、初始条件、Y′(0)均可由统计数据得到，得到方程可解，其特征根为：

μ1=(-α+(α2-4β)1/2)/2,

μ2=(-α-(α2-4β)1/2)/2.

经验算可知F/s为方程的一个特解，对根的几种情况进行讨论:

1) 当α2>4β时，μ1、μ2均为实数，通解为

Y(t)=φeμ1t+ωeμ2t+F/s.

2) 当时α2<4β，μ1=μ2=-α/2，通解为

Y(t)=(φ+ωt)e2(μi)+F/s.

Y(t)=heμtsin(vt+w)+F/s.

根据上述得到的数学模型，查阅资料，并从总体上看粮食供需矛盾，分析得到供需预测表(表1).

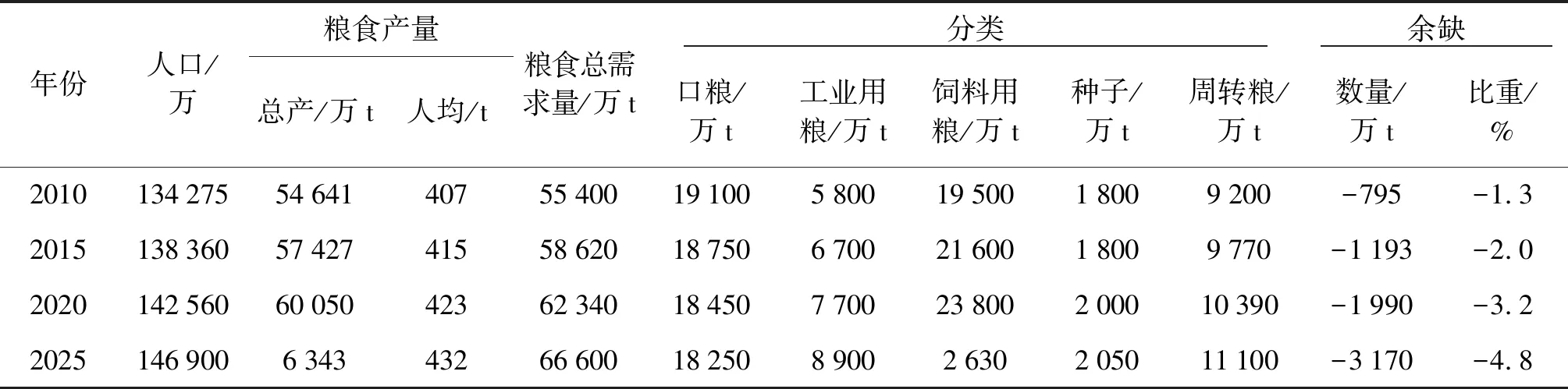
表1 人口、粮食产量及需求预测表

注：人口从2010年后按0.6%增长测算，粮食产量从2010以后各年增幅按16测算；粮食需求:口粮农村年均减速1.4%测算，城镇按增幅2.1%测算；工业用粮从2010年后按3%增速计算；饲料用粮按肉、蛋、奶、鱼产量乘以肉1.8、蛋1.7、奶0.4、鱼0.8系数求得.改革开放30年饲料用粮年均增幅为5%，以后各年按增2%测算，种子按产量3x计算；周转粮即库存按消费量的20%计算，从表上可以看出2010年粮食缺口达759万t，占需求量的1.3%.若今后20年产量按1%增长，粮食缺口将逐步扩大，到2020年缺口达1 990万t，2025年缺口增加到3 170万t，比重上升到4.8%.

经查阅计算得到城市化水平每提高1%，耕地面积减少0.51%，粮食总产量减少1.16%，综合影响因素引起的粮食需求量是87 136万吨.

L=0.291，s=0.019，m=1，a=0.8,

a=Ls+m-l，ma=0.773，B=Lsm=0.005 46.

特征根μ1=0.007，μ2=-0.78，由Matlab解微分方程得出解为

Y(t)=φeμ1t+ωeμ2t+F/s,

Y(t)=351 528.9e(0.007t)+47 602.9e(-0.78t)-348 500.

方程的初始条件从2010年开始作为第0年，所以当t为9、10、11、12、13时即代表2019, 2020，2021，2022，2023年的粮食总产量.

预测出总产量如表2所示.

表2 粮食总产量预测表

利用散点图拟合出线性曲线，从而利用线性方程计算出预测值.

粮食单位面积散点图(图2)为：

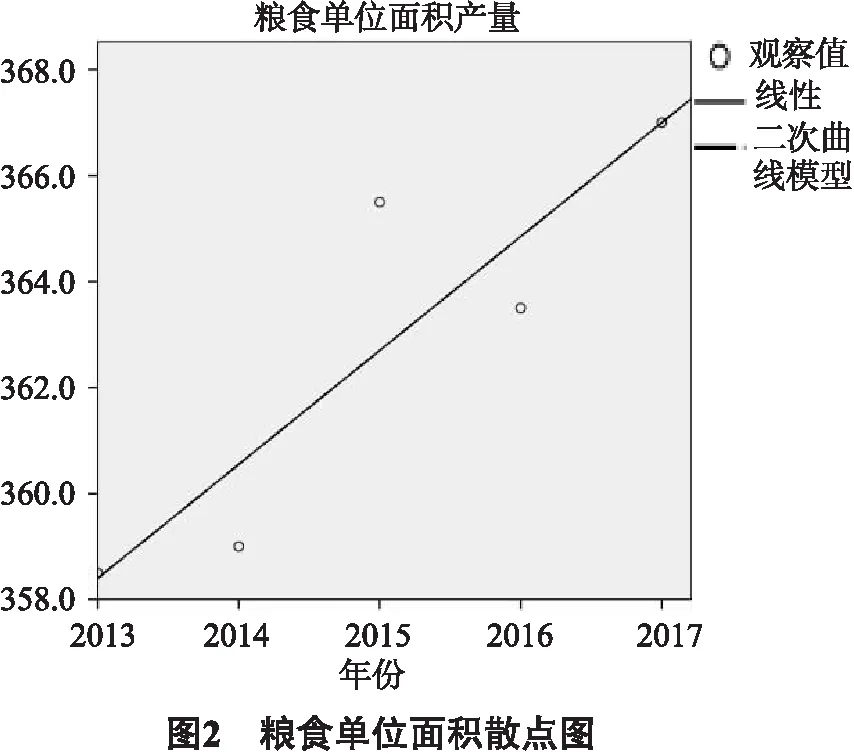
耕地面积散点图(图3)为：

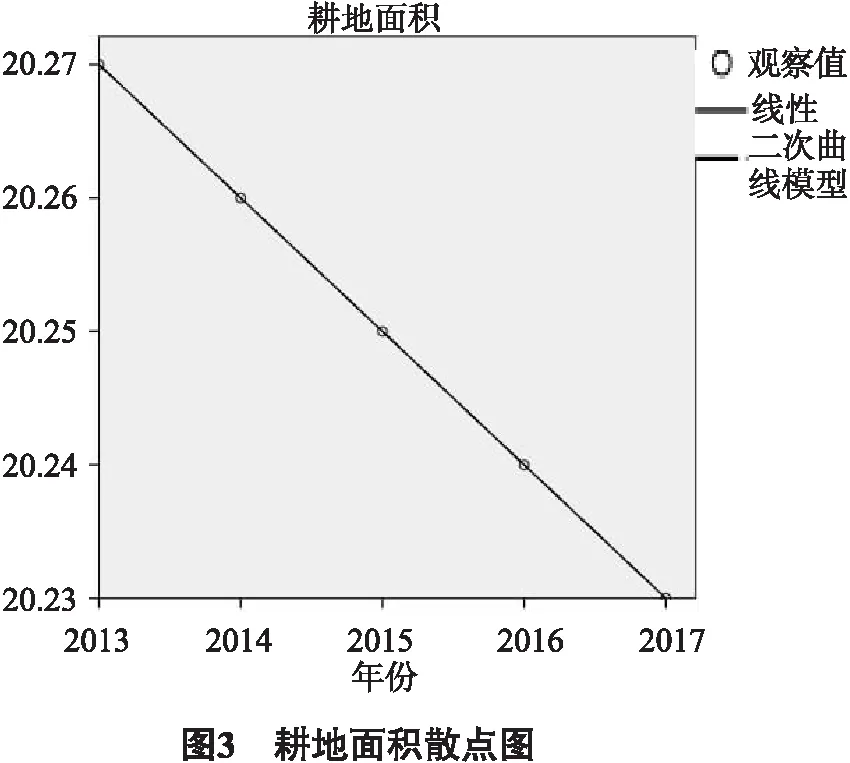
用逐差法求得粮食单位面积产量、耕地面积平均每年的增长量，就是线性方程的斜率，即分别求得粮食单位面积产量、耕地面积的线性方程为：

y=2.13x-3 929.3,

y=-0.01x+40.4,

其中x表示年份，y表示因变量.

预测数据如表3所示.

表3 粮食单位面积产量、耕地面积预测数据表

然后，拟合预测出的总产量与轮耕面积的散点图(图4)为：

得到总产量与轮耕面积的线性方程为：

y=1.875 9x-114 862.

最后，得出在国家粮食安全保障的基础下我国5年后可轮耕土地面积为6 286.909万亩.

为了进一步求解研究内容提出的问题，搜索数据得到表4所示.

表4 轮耕面积、财政收入与投入数据表

拟合财政收入和财政投入的线性曲线图：

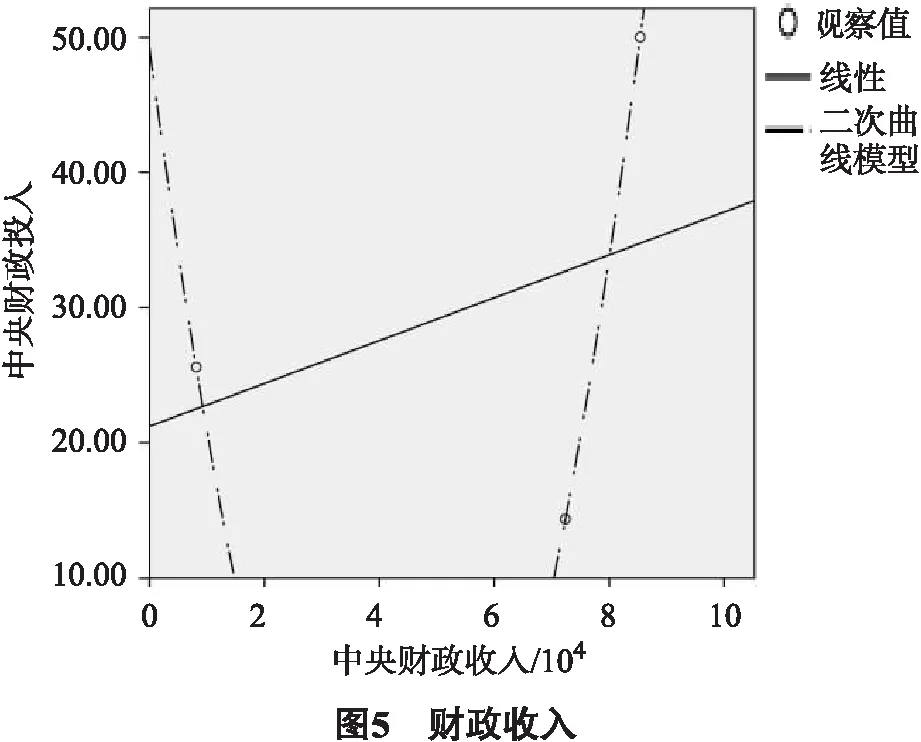
拟合财政投入和轮耕面积的线性曲线图(图6).

根据财政收入和财政投入、财政投入和轮耕面积两组数据的拟合，得到如下线性方程：

y=0.002 5x-170.89,

y=49.915x-91.499.

由上述线性方程预测出我国五年后每年的土地轮耕面积，以及每年国家财政的投入数据表(表5).

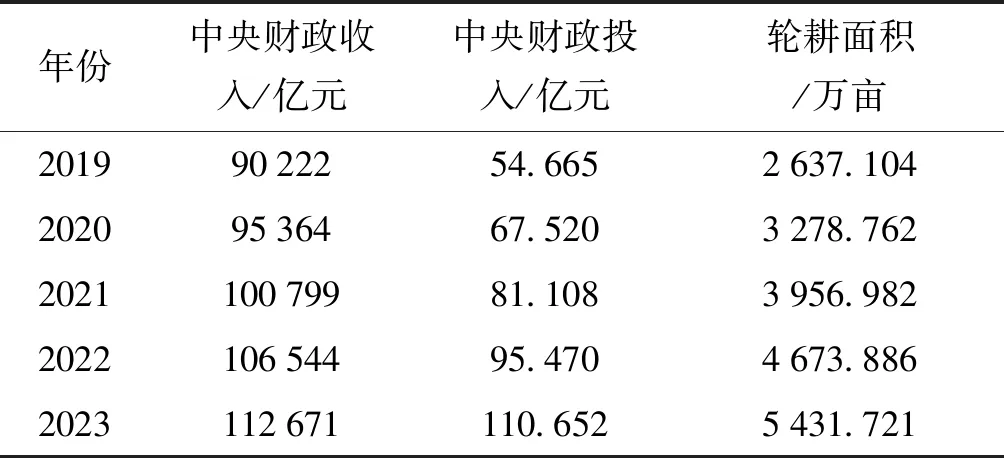
表5 预测数据表

3 模型检验

3.1 样本回归模型的检验

表6 样本回归模型的检验结果

表7 方差分析

关于样本回归模型的拟合优度检验，从回归统计输出结果可知，可决系数RSquare为0.999 824，调整后的可决系数也约为0.999 648，说明样本回归模型的方程拟合效果很好，表明我国土地轮耕的面积的增长中，99.9%是由于中央政府补贴资金的拉动作用.

关于回归方程的显著性检验，从方差分析输出结果可知，F统计量的P值为0.008 445 853，显然小于显著性水平0.05(置信度默认为95%)，所以该样本回归模型的方程显著，因此中央政府补贴资金对土地轮耕面积有显著影响.

3.2 灰色预测模型的检验

预测数据为：

G1=20.21、20.20、20.19、20.18、20.17，

G2=90 222、95 364、100 799、106 544、112 671，

G3=54.665、67.520、81.108、95.470、110.652，

G4=2 637.104、3 278.762、3 956.982、4 673.886、5 431.721.

其中，G1表示5年后我国可轮耕土地面积；G2表示至2023年每年中央财政收入；G3表示至2023年每年中央财政的投入；G4表示至2023年每年的土地轮耕面积.

相对残差Q检验：Q1=0.005，Q2=0.076，Q3=0.081，Q4=0.004，相对残差的平均值为0.041 5，4.15%小于5%，因此模型建立较好，预测结果精度高.

小误差概率P检验：P1 =0，P2 =0.2，P3 =0.1，P4 =0.15，小误差概率都小于1，模型的误差很小，充分说明模型精度较高.

3.3 模型结果分析

采用样本回归模型，用已知的数据分析出样本线性回归方程，以此来表示总体的回归模型，从而计算出当轮耕影响粮食产量达到5%时，中央财政预计需要安排的专项补贴资金.并且通过函数、数组、回归分析工具等方法的检验，得出模型能较好的对研究内容进行预测和计算.

灰色预测模型的建立使其问题简单化，且该算法需要的信息少且通用性强.本题中我们通过对2013—2017年短期内每年的主要粮食产量做出预测.观察实际值与观测值的相对误差，预测出未来5年的主要粮食产量，从而预测出未来5年我国土地的轮耕面积.通过模拟预测检验，得到灰色模型的预测结果具有一定的可靠性.

运用线性回归分析，拟合出数据之间的曲线图，从而得到线性回归方程，以此来预测出至2023年我国每年的土地轮耕面积，以及每年国家财政的投入.

4 结语

回归模型是一种预测性的建模技术，它研究的是因变量(目标)和自变量(预测器)之间的关系.这种技术通常用于预测分析，时间序列模型以及发现变量之间的因果关系.回归模型重要的基础或者方法就是回归分析，回归分析是研究一个变量(被解释变量)关于另一个(些)变量(解释变量)的具体依赖关系的计算方法和理论，是建模和分析数据的重要工具.在这里，我们使用曲线或线来拟合这些数据点，在这种方式下，从曲线或线到数据点的距离差异最小.

在不确定性和贫信息性系统的问题领域中,灰色系统理论具有十分广阔的发展前景.灰色预测法的基本思想是通过鉴别系统因素之间发展趋势的相异程度，既进行关联分析，并对原始数据进行生成处理来寻找系统变动的规律，生成有较强规律性的数据系列,然后建立相应的灰色预测模型.可广泛的应用于社会科学，自然科学领域，系统地分析、建模、预测、决策的问题中.因此灰色预测模型能够运用到养殖业、种植业、水产业等相关产业的产品产量的分析预测.