基于集成建模的空间光学望远镜稳像验证方法

徐广德 张柏楠 王杰 孙国童 苟仲秋

(中国空间技术研究院载人航天总体部，北京 100094)

为实现高分辨率成像，空间光学望远镜除了要求主镜尺寸尽可能大以外，还要求极高的指向稳定度。如哈勃空间望远镜(HST)[1-2]、詹姆斯·韦伯空间望远镜(JWST)[3-4]要求指向稳定度小于0.007″(1σ，表示1倍的标准差分布)，正在论证的美国太阳系外行星探测计划(ACCESS)要求指向稳定度小于0.000 1″(1σ)[5-7]。为了达到高稳定度，空间望远镜通常采用多种稳像手段相结合、分频段治理的方案。HST采用高性能的陀螺和导星仪作为测量设备，以动量轮为执行机构，通过高带宽姿态控制抑制中低频扰动实现整体的惯性稳定指向，同时对于动量轮和太阳翼造成的扰振采用了隔振措施。JWST采用粗精两级的稳像控制方案，在平台姿控基础上，通过在载荷内部引入精密稳像控制，实现对中低频抖动的抑制，并采用了动量轮隔振器、平台载荷舱间阻尼杆减振器等隔振措施，抑制高频抖动的影响。

对于大型空间望远镜而言，受重力卸载条件限制，在地面难以做全链路的稳像试验[8]，因此集成建模与仿真对于验证系统稳像方案、考核指标极为重要。集成建模是将影响系统关键性能的各分系统模型进行集成，形成一个能全面反映各种耦合效应的系统级动态输入输出数学模型。对于空间望远镜来讲，就是将影响指向稳定度的结构模型、控制模型、光学模型和扰动模型集成为一个系统模型。集成建模既可以从系统层面指导设计，也可以对系统方案进行集成验证。国外在空间望远镜设计和验证中常采用集成建模方法[9-12]，如JWST采用集成建模的方法对系统的关键指标如斯特列尔比、波像差进行验证[12]。国内对集成建模方法的研究以遥感卫星微振动响应分析为主，文献[13]建立了遥感卫星结构-控制-光学一体化模型，并对微振动响应进行了分析。文献[14]提出了一种通过单机和分系统试验、集成建模仿真验证制冷机对相机成像影响的微振动分析方法。以上研究只考虑了高频扰动通过结构传递至相机光机结构产生的微振动响应，对中低频扰动和噪声的影响缺少建模和分析。

为了从系统层面评估和验证空间光学望远镜的稳像方案，本文研究了结构、光学、扰动、姿控、稳像控制一体化集成建模方法。首先，从保证成像质量角度分析了空间光学望远镜对指向稳定度的需求；进而，梳理了指向稳定度的影响因素，并给出了一种典型系统稳像方案。基于该方案建立了结构、光学、扰动、姿控、稳像控制一体化集成模型，最后通过仿真对稳像方案进行了验证，定量分析了各因素对光轴指向的影响。

1 稳像需求与影响因素分析

为保证成像质量，空间光学望远镜对指向稳定度提出了远超常规航天器的需求。HST在可见光波段的衍射极限分辨率约为0.064″，为保证指向晃动不使角分辨率下降超过10%，对单次曝光时间内(从10 s到24 h)的指向稳定度提出了0.007″(1σ)要求。JWST工作在红外波段(0.6～28.5 μm)，80%能量集中度动态角分辨率指标为0.1″，对光轴指向稳定度要求也为0.007″(1σ)。参考HST和JWST，对于一个1.5 m口径的光学望远镜，在可见光波段的极限分辨率约为0.1″，为保证指向晃动不使角分辨率下降超过10%，曝光时间100 s内的指向稳定度要求不大于0.01″(1σ)。

与对地遥感卫星不同，空间光学望远镜通常需要进行长曝光成像，因此宽频带内的扰振和噪声都会影响成像期间的指向稳定度，进而对成像分辨率造成影响。此类航天器内外存在各种各样的扰振源，如表1所示。外部扰源主要为环境干扰，如大气阻力、太阳光压等产生的干扰。典型内部扰源的如反作用轮或控制力矩陀螺、机械陀螺、太阳翼和天线驱动机构，以及载荷内部各种运动机构如制冷机、扫描镜等。除了内外干扰外，测量噪声也会对指向稳定度造成影响，不论整星的姿态控制还是载荷内部的稳像控制，所采用敏感器的测量噪声都会经过闭环控制影响控制输出。

扰振可以划分为瞬态扰振和稳态扰振两大类，稳态扰振又分为周期性扰振和随机扰振。如果扰振频率成分主要在低频段，无论整星还是除了柔性附件外的中心刚体都相对质心产生姿态响应，指向稳定度采用姿态进行描述。如果频谱扩展到更高频率，扰振力和力矩通过卫星本体和载荷结构传递，激起各个部位的振动。扰振量级很小，产生的振动通常也很小，位移在微米量级，加速度在10-3gn量级，这种振动通常被称为微振动[15]。在高频段，不再分中心体还是附件，整星表现为柔性，不再用姿态定义指向稳定度，通常用载荷成像焦面对应的视线(LOS)抖动来表述。

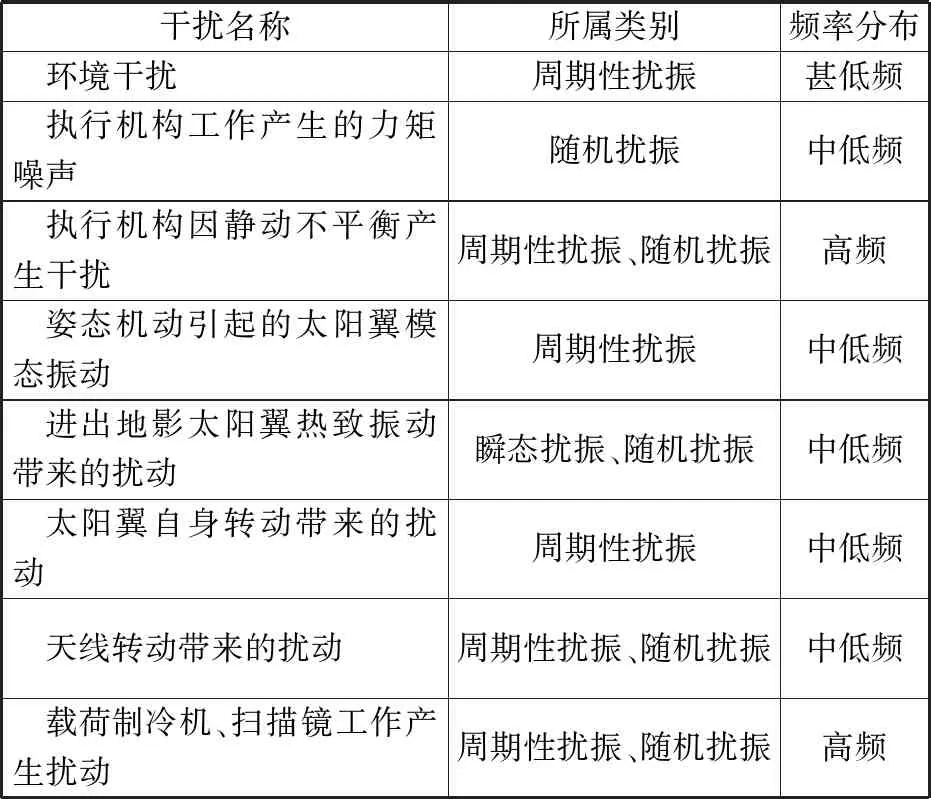
表1 干扰频率分布Table 1 Disturbance frequency distribution

由上面分析可知，在不同的频段，系统对扰振的响应不同。一般情况下，按照频率分布，指向稳定度可分为低、中、高三个频段[15]。

(1)低频段(典型的频段分布为0～1 Hz)：在该频段，整个飞行器表现为刚体，通常采用姿态控制方法抑制低频扰动影响，稳定飞行器的姿态指向。

(2)中频段(典型的频段分布为1～10 Hz)：在该频段，太阳翼、中继天线等表现为柔性附件，平台和载荷仍表现为刚体。姿态控制受控制带宽所限，对此频段扰动已无抑制能力。可在载荷中采取稳像控制措施，通过调节光线补偿光轴抖动。

(3)高频段(典型的频段分布为从10 Hz到1000 Hz)：在该频段，整个飞行器表现为柔性体，姿态控制和稳像控制都失去作用，高频扰振通过星体结构传递载荷光机结构，导致镜面和成像焦面的抖动。应避免结构频率与扰动频率相近造成共振，同时通过引入隔振器改变结构传递特性，实现对扰动的抑制。

2 典型稳像方案

通过以上对指向稳定度影响因素的梳理，本文以1.5 m口径空间光学望远镜为例，拟采用整星姿态控制加载荷稳像控制的方法实现对中低频视线(LOS)抖动的抑制，以及采用被动隔振方法抑制高频振动引起的LOS抖动，满足0.01″(1σ)的稳像需求。

整星姿态控制采用星敏感器和陀螺进行姿态确定，通过陀螺积分产生姿态四元数，并利用星敏数据通过卡尔曼滤波估计对陀螺漂移和积分得到的姿态四元数进行纠正。执行机构为五棱锥构型控制力矩陀螺群。控制器包括比例-积分-微分(PID)控制器和一个二阶滤波器，来抑制太阳翼模态振动，控制带宽约0.1 Hz。

载荷稳像控制参考JWST[4]，为双轴快摆镜(FSM)视线稳定控制，敏感器为导星仪，执行机构为FSM，控制带宽约10 Hz。利用面阵探测器作为导星仪，检测精度为0.01″(3σ，表示3倍的标准差分布)。快反镜由镜体结构、柔性支撑、差分阻抗传感器和音圈电机组成，音圈电机通过推拉方式驱动将平移运动转化为镜体的小角度转动。

高频干扰主要为控制力矩陀螺工作产生的高频扰振力和力矩，拟在平台和载荷之间通过被动隔振改变结构动力学特性，实现对高频扰振的衰减。

3 集成建模

根据第2节典型稳像方案可得系统数学模型(见图1)，本节分别建立结构模型、姿态控制模型、稳像控制模型和光学模型，最后得到集成模型。

图1 稳像方案数学模型Fig.1 Mathematical model of LOS stabilization

3.1 结构模型

通过对结构的有限元模态信息进行处理完成结构建模，结构模型除星体结构外还包含了隔振器的模型。基于有限元模型建立无阻尼结构动力学方程[16]为

(1)

式中：M∈Rn×n为质量矩阵；K∈Rn×n为刚度矩阵；x∈Rn×1为节点位移；F∈Rn×1为输入载荷；n为自由度；R为实数集。

节点位移坐标x和模态坐标ξ有如下关系[16]

x=Φ0ξ

(2)

式中：ξ∈Rn×1为模态坐标；Φ0∈Rn×n为质量归一化振型矩阵。

(3)

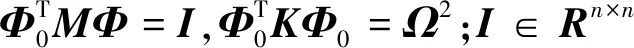
加入阻尼矩阵Z，并将外力F分解为控制输入uc和外力扰动d，式(3)可写为

(4)

(5)

取输出为姿态敏感器节点的3个转动自由度的转动角度yc，以及光学元件的6自由度位移yo，则输出方程为

(6)

令Cpc=[Cy1xΦ00]，Cpo=[CyzxΦ0]，式(6)可改写为

(7)

式中：Cpc∈R3×2n；Cpo∈Rm×2n。

3.2 姿态控制模型

姿态控制模型采用3个独立的PID控制器和二阶滤波器结合的形式，单通道的传递函数模型[13]为

(8)

式中：s为复变量；kp为比例增益；kd为微分增益；ki为积分增益；ω1为滤波器转折频率；ξ1为滤波器阻尼。

三轴姿态控制器采用状态空间模型可表示为

(9)

式中：qc∈Rnc×1为姿态控制器模型状态向量，nc为姿态控制器状态向量维数；Ac∈Rnc×nc为状态矩阵；Bc∈Rnc×6为输入矩阵；Cc∈R3×nc为输出矩阵；Dc∈R3×nc为前馈矩阵；yc∈R6×1为陀螺测量的三轴姿态角速度和星敏测量的三轴姿态角；wc∈R6×1为测量噪声；uc∈R3×1为三轴控制输出力矩，分别加载在结构模型的控制输入节点的3个转动自由度上。

3.3 稳像控制模型

稳像控制器模型为两维独立的控制器，单通道控制器包括一个超前校正器和两个低通滤波器，其传递函数模型[17]为

(10)

式中：K为增益系数，z1和p1为超前校正器的参数，p2和p3为低通滤波器参数。

稳像控制器模型(10)采用状态空间可表示为

(11)

式中：ql∈Rnl×1为稳像控制器模型状态向量，nl为稳像控制器状态向量维数；Al∈Rnl×nl为状态矩阵；Bl∈Rnl×2为输入矩阵；Cl∈R2×nl为输出矩阵；Dl∈R2×nl为前馈矩阵；z∈R2×1输入为导星仪测量的LOS抖动；wl∈R2×1为导星仪测量噪声；ul∈R2×1为二维快摆镜转角。

3.4 光学模型

光轴定义为载荷主光路通过光瞳中心的光线，在理想状态下，光轴的方向应与本体坐标系的X轴重合。受到微振动源引起的扰动后，光轴的方向会产生偏差。光学模型的表现形式为光学灵敏度矩阵，其描述光学元件运动与光轴运动的关系。

当稳像系统不工作时，该模型的输入是光学有效载荷上各光学元件(反射镜)安装位置的6自由度振动位移yo，输出为光轴绕本体系Y轴和Z轴的转角z，即LOS抖动。利用光学灵敏度矩阵，可得光学输出方程为

z=K11yo=K11Cpoqp

(12)

式中：K11∈R2×m为载荷光学系统的光学灵敏度矩阵。

当稳像系统工作时，快摆镜发生二维转动导致光线发生变化，此时光学模型的输入除了各光学元件的6自由度位移yo外，增加快摆镜的二维转角ul带来的影响[16]。

z=K11Cpoqp+K12K2ul

(13)

式中：K12∈R2×2为快摆镜二维转动对应的光学灵敏度矩阵；K2∈R2×2为快摆镜耦合系数矩阵，与快摆镜到焦面的距离有关。

3.5 集成模型

参考文献[16]，将式(5)、(7)、(9)、(11)和(12)集成为

(14)

则以q=[qpqcql]T为状态变量，输入为干扰和噪声w=[dwcwl]T，输出为光轴抖动z，可得集成状态空间模型为

z=Czwq+Dzww

(15)

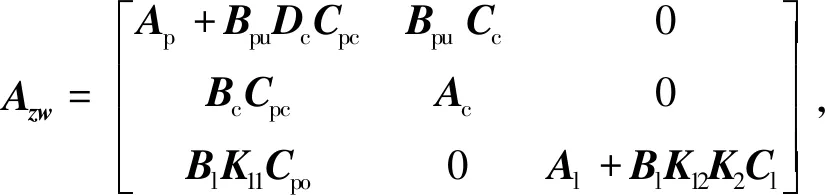
为了得到频域响应，通过对式(15)拉氏变换可得从扰动、噪声到光轴抖动的闭环传递传递函数矩阵[13]为

G(s)=Czw(sI-Azw)-1Bzw+Dzw

(16)

4 仿真验证

以典型空间光学望远镜稳像方案验证为例，首先通过与NASTRAN软件进行传递率对比验证集成建模方法的正确性，随后采用该方法对系统稳像方案进行验证。

4.1 集成建模输入

(1)整星的有限元模型共有10 872个节点和11 459个单元。

(2)高频扰振输入为6个CMG的扰动力和力矩，给定的CMG扰动力Fx，Fy，Fz和力矩Mx，My，Mz，由谐波叠加组成，各谐波频率的扰动力和力矩幅值如表2所示，具有较强的宽频特性[13]。

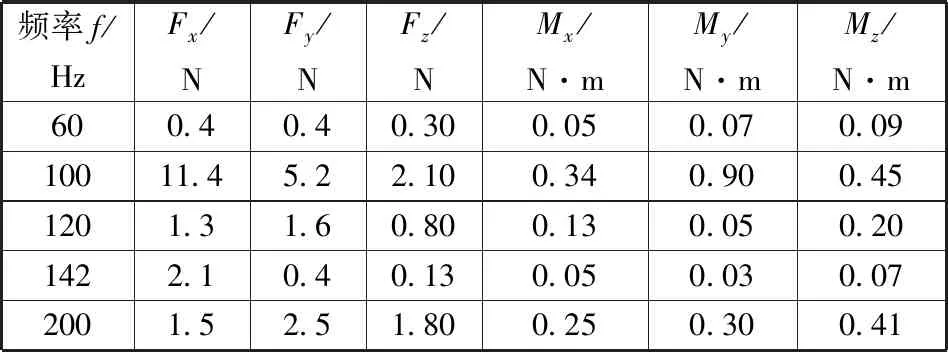
表2 CMG 扰振特性Table 2 Disturbance of CMG

(3)陀螺的姿态角速度测量噪声为0.000 1 (°)/s(3σ)。

(4)星敏的姿态角测量噪声为1″(3σ)。

(5)导星仪的测量噪声为0.01″(3σ)。

(6)CMG的力矩噪声为0.01 N·m(3σ)。

(7)环境干扰力矩Td1(t)=0.000 1 sin(2πft)，f=2×10-4Hz。

(8)太阳翼扰动力矩为Td2(t)=0.1 sin(2πf1t)+0.1 sin (2πf2t) Nm，f1=0.1 Hz，f2=0.6 Hz(f1、f2为太阳翼前两阶模态频率)。

(9)姿态控制器参数为kp=1.97×104,ki=200,kd=4.44×104。

(10)稳像控制器参数为z1=11.06,p1=138.2,p2=2.76,p3=0.28,K=1000。

(11)望远镜的灵敏度矩阵由光学设计软件Zmax计算得到，所研究的光学系统模型是同轴三反光学系统，由主镜、次镜、三镜和焦面组成。依次对镜面和焦面进行位置和姿态的小范围调整，计算像移并除焦距得到光轴抖动，可获得灵敏度矩阵。

4.2 集成建模方法验证

由以上扰动源模型、整星结构模型、控制系统模型和光学系统模型集成为一体化分析模型，模型中反映干扰特性、噪声特性、卫星的结构传递特性、姿态控制系统的控制律、稳像系统的控制律以及光学系统的光路传递特性。为了验证集成模型的正确性，利用NASTRAN与建模结果进行比对，采用计算得到的集成模型开环传递特性与NASTRAN分析结果对比。以6个CMG其中一个的Fy到LOSZ的传递率为例，两种方法得到的传递率结果如图2所示。

图2 集成建模与NASTRAN传递率结果对比Fig.2 Comparison of transmissibility between integrated model and NASTRAN

由图2可以看出，通过集成建模得到的开环传递率与NASTRAN计算结果一致，验证了集成建模方法及得到的集成模型的正确性。

4.3 典型稳像方案验证

根据建立的集成模型，以CMG扰振为例，可得到在不同稳像方案下CMG扰振到LOS抖动的传递函数如图3所示。可见，与开环传递函数相比，通过整星姿态控制可以对低频扰动进行抑制，采用稳像控制后进一步提高了低频抑制能力，通过引入被动隔振大幅衰减了高频扰振对光轴的影响。

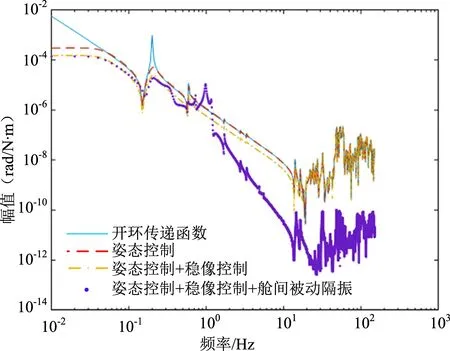
图3 不同稳像措施下CMG扰振力矩到 光轴的传递率曲线Fig.3 Transmissibility curves of different LOS stabilization methods from CMG’s disturbance to LOS

依据集成模型开展频域仿真，得到姿态控制敏感器(星敏、陀螺)测量噪声、稳像控制敏感器(导星仪)测量噪声、环境干扰、活动部件干扰(太阳翼、CMG)等对LOS抖动的贡献(见表3)，可见总的LOS抖动约0.005″(1σ)。

表3 各影响因素对LOS抖动的贡献Table 3 Contribution to LOS jitter of all factors

进一步依据集成模型开展时域仿真，得到LOS抖动结果如图4所示，可见满足不大于0.01″(1σ)的指标要求。通过以上系统传递率分析、频域仿真和时域仿真，验证了系统稳像方案的有效性。

4.4 讨论

通过将结构模型、姿态控制模型、稳像控制模型、光学模型等集成为一体化模型，可系统地分析在各种扰源和噪声作用下的动态响应，验证稳像设计方案的正确性和指标满足度。此外，集成模型也用于系统设计参数的权衡，在获得扰振和噪声特性情况下根据集成建模仿真结果进行针对性的方案优化。

5 结束语

本文给出了一种通过集成建模仿真验证空间光学望远镜稳像方案的方法，系统地考虑了干扰、噪声、姿态控制、稳像控制、结构动力学特性等影响因素，建立了集成仿真模型，通过与NASTRAN软件比较传递率验证了集成建模与仿真方法的有效性。综合考虑了各种扰动和噪声，可得到全频带的光轴抖动分布特性，并可通过频域仿真、时域仿真得到总的光轴抖动，本文的研究结果可为空间光学望远镜的稳像方案系统验证提供参考。拟后续开展模型修正研究，通过试验测试得到扰源特性、噪声特性、结构动力学特性等，进而修正集成模型，基于修正后的模型开展集成仿真可获得更接近真实的光轴特性。