某车载防空系统行进间发射动力学仿真分析与研究*
2019-07-30麻小明刘馨心李正宇胡建国
麻小明,刘馨心,李正宇,李 庚,胡建国
(西安现代控制技术研究所, 西安 710065)
0 引言
车载防空系统作为一种由运动平台搭载的武器系统,在未来战争中担负着快速机动、地面突防、压制、防空等高科技武器装备的重任[1]。美国对未来战斗系统的要求是:能够在静止或运动中对多个目标进行探测、捕获、识别、打击、杀伤和判定损伤程度;能全方位与地面和空中目标交战。科学技术的进步不仅要求武器系统能够精确打击目标,而且具有较高的生存能力。具有行进间发射能力的车载防空武器系统,在面对敌方攻击时其空窗期比较短,在转移阵地的过程中就可以实施反击。文献[2-3]分别利用谐波叠加法、AR模型法建立了三维随机路面,利用多体动力学软件对轮式和履带式车载武器进行了行进间发射动力学仿真,获得了车速对车载武器性能的影响。
文中基于多体动力学软件LMS Virtual. Lab Motion搭建车载武器系统,考虑行进间发射时所受的各种环境因素,在符合国家标准的路面上进行仿真分析与研究,得到该防空武器系统行进间发射的安全包络区间,为提高该武器系统行进间发射的发射精度、发射稳定性以及发射安全性等提供理论支撑。
1 路面激励
车辆在行驶过程中,路面不平度会激起车辆的振动,这种振动属于随机激励,会对车辆行驶平顺性、发射精度、发射稳定性等造成较大影响,因此在分析过程中建立合理精确的路面模型至关重要。
1.1 路面不平度
路面不平度是指道路表面相对已知理想基准平面的偏离程度,路面不平度是一组在时间域上各态历经的无限长随机信号。随机信号在各时间点上的值是不能先验确定的,它的每个实现往往是不同的,因此无法像确定信号那样用数学表达式或图表精确的表示,而只能用它的各种统计平均量来表征。功率谱密度就是随机信号的一种最重要的表征形式[4]。
国际标准化组织(ISO)和我国GB7031-2005均建议采用下式功率谱密度函数拟合:
(1)
式中:n为空间频率,它是波长λ的倒数,表示每米长度中包括几个波长,单位m-1;n0为参考空间频率,n0=0.1 m-1;Gq(n0)为参考空间频率n0下的路面谱值,称为路面不平度系数,单位m2/m-1;W为频率指数,为双对数坐标上斜线的斜率,它决定路面谱的频率结构。
1.2 谐波叠加原理
谐波叠加法基本原理是认为路面不平度可由大量正弦波组成,其数学推理严格,虽然涉及到许多三角函数,运算量大,耗时较长,但是生成的路面模型准确性较好,使用广泛[5]。
式(1)是基于空间频率的表达式,由车速和时间频率之间的关系可以写出时域下的表达式:
f=vn
(2)
(3)
式中:f为时间频率,单位Hz;v为车速,单位m/s。
路面不平度的方差可以表示为:
(4)
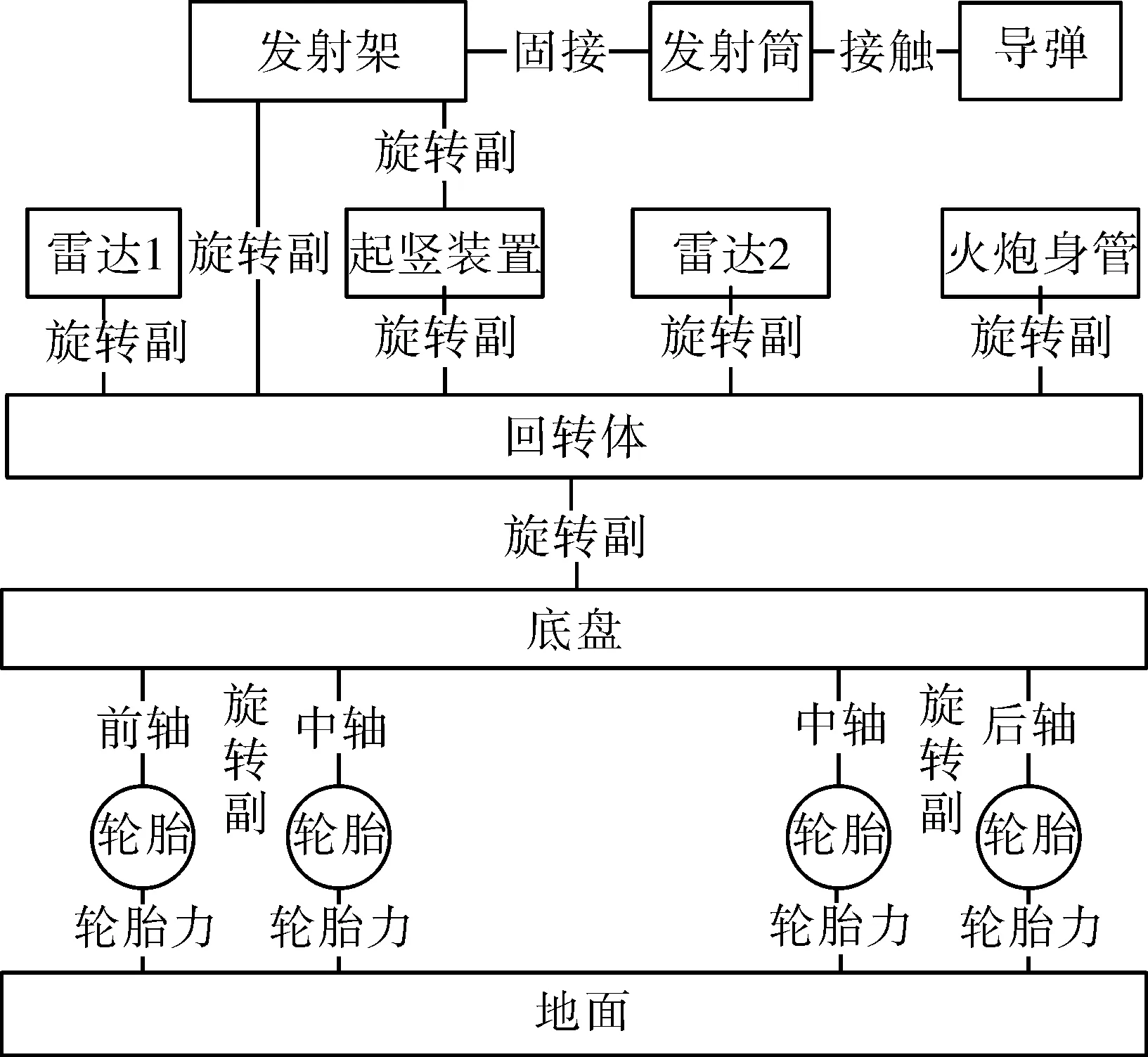
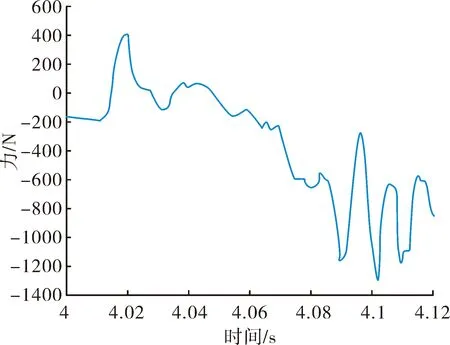
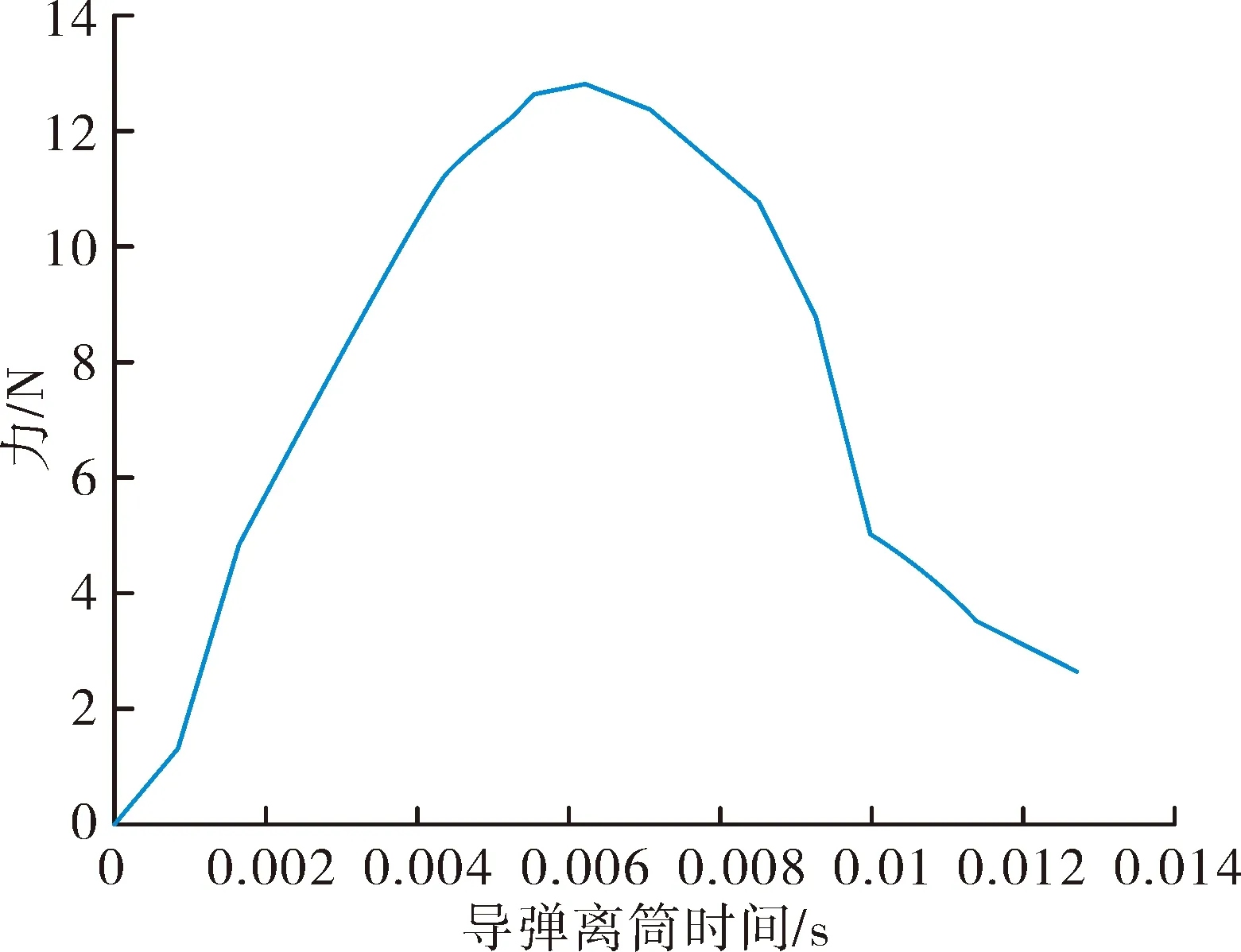
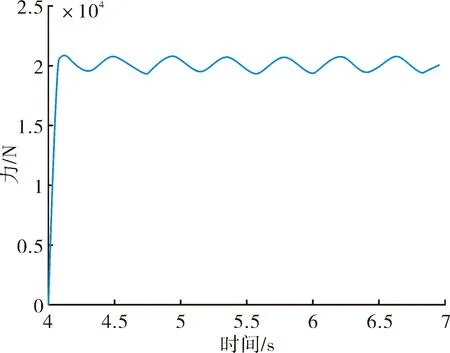
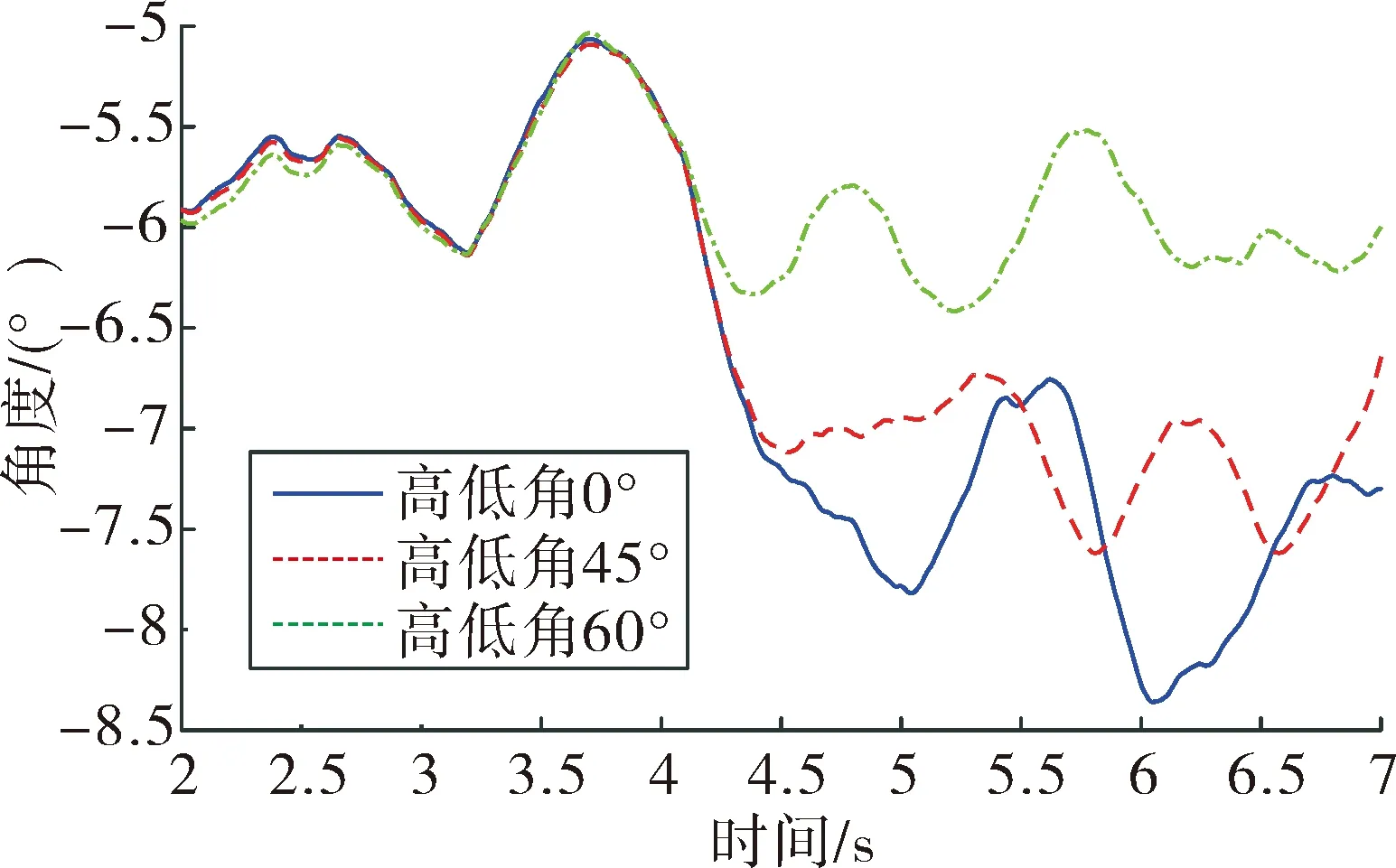
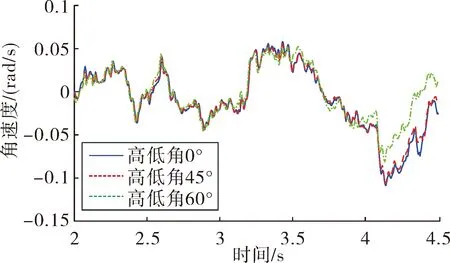
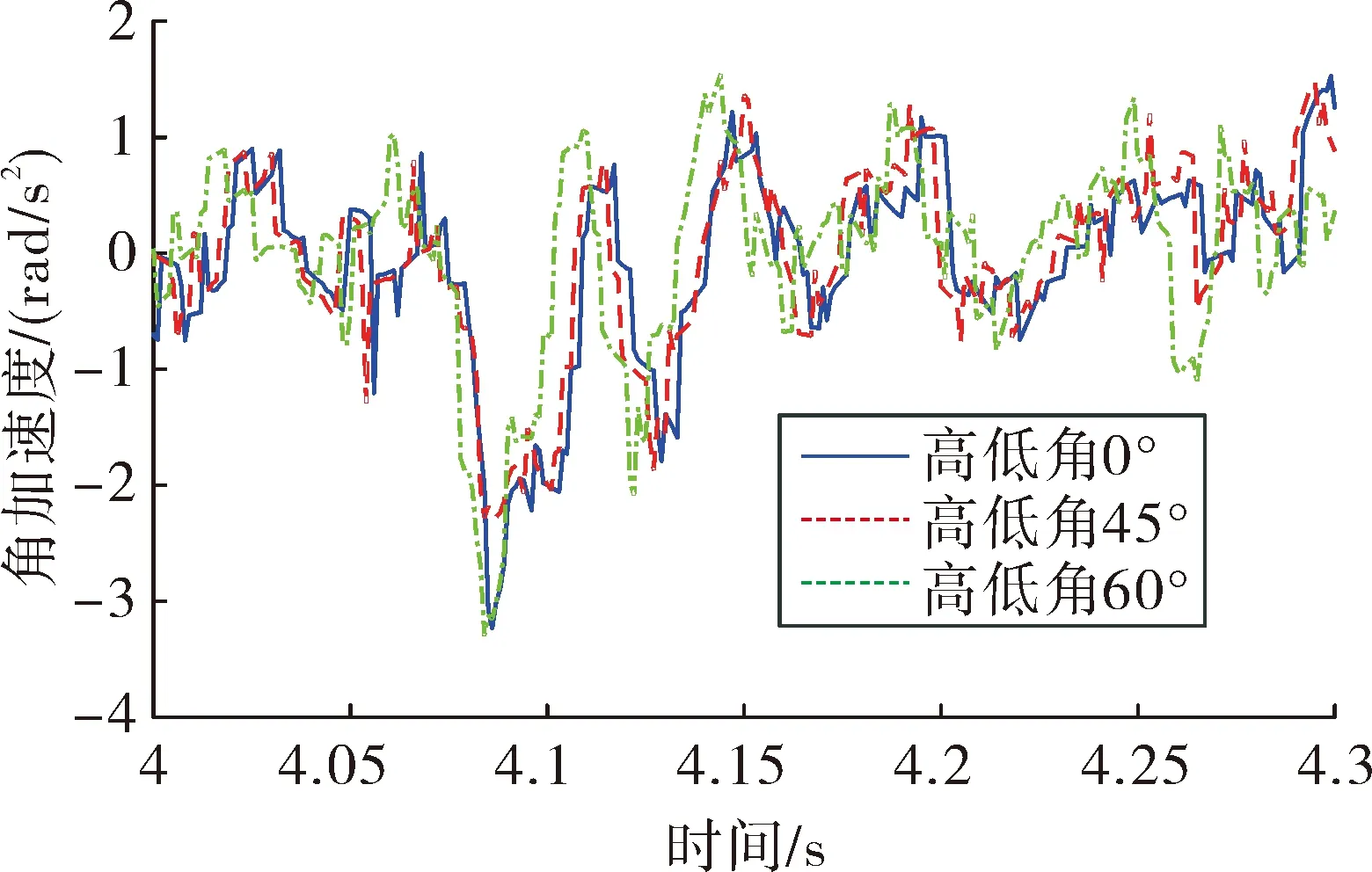
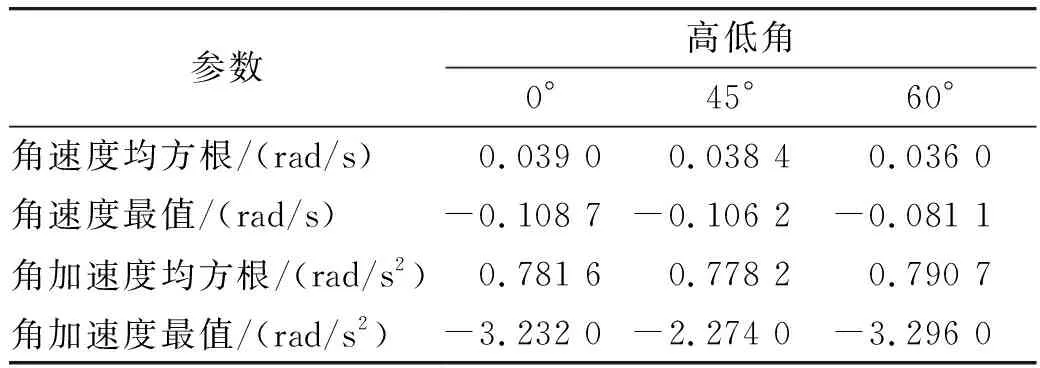
将f(fmin (5) 第i小区间的功率谱为: w=Gq(fmid,i)δfi (6) 由功率谱和幅值谱的关系|A2|=w得到每段频率所对应的不平度幅值为: (7) 将N个正弦波叠加就可得到随机路面垂直位移的时域表达式: (8) 式中:q(t)为时域下路面高程;θi为[0,2π]的随机数。 将式(8)写成空间域内的表达式: (9) 根据谐波叠加法,采用Matlab数学工具编写计算程序,生成符合我国道路分级标准的1 000 m长的D级路面,如图1所示。对模拟生成的路面进行验证,由图2可以看出模拟路面能够较好的反应真实路面状况。 图1 D级二维路面 图2 功率谱密度 将式(9)扩展为x方向和y方向,得到三维空间下的路面不平度关系式: (10) 式中:θi(x,y)为均匀分布在[0,2π]上的相互独立的随机变量;x,y为路面纵横向行程,单位m;q(x,y)为三维空间内的路面高程,单位m。 利用Matlab生成宽5 m长80 m的三维路面,如图3所示。 图3 D级三维路面 车载防空系统结构复杂,在建模过程中根据其特点可以划分为轮胎、底盘、回转部分(包括发射架、发射筒、导弹)、雷达和火炮这五大部分,模型拓扑结构如图4所示。 在发射时刻,整车所处的环境非常复杂,除了来自地面的随机激励,还受到导弹发射时的反作用力以及汽车发动机引起的振动,需作如下假设:忽略发动机引起的振动,驱动力直接作用于车轮;不考虑结构之间的间隙,假设约束为理想约束;部件变形引起的变化相对于路面引起的变化较小,因此可以忽略。 图4 动力学模型拓扑结构 模型施加载荷如下:根据实验获得导弹的反作用力,如图5所示,通过理论计算得到导弹燃气流冲击力,如图6所示,根据经验得到火炮反作用曲线,如图7所示。 图5 导弹反作用力曲线 该防空系统采用轮式汽车底盘,轮胎的结构参数和力学性能对于汽车行驶平稳性起到重要作用,因此建立合理精确的轮胎力单元至关重要。LMS Virtual.Lab Motion提供了精确的轮胎模型。轮胎所受作用力包括竖直力、侧向力、纵向力3个方向的力和回正力矩、滚动阻力矩、倾覆力矩3个力矩;车辆在行驶过程中,轮胎还会发生外倾和侧偏,外倾角是轮胎平面偏离竖直平面的倾斜角,侧偏角是车轮行程方向和车轮指向的夹角,Virtual.Lab Motion在计算时考虑了模型中的外倾角和侧偏角,并且考虑了轮子的转动惯量[6]。 图6 导弹燃气流冲击力 图7 火炮后坐力曲线 仿真建立的坐标系描述如下:X轴与前进方向相反,Z轴垂直地面向上,Y轴符合右手法则。载车行驶速度为30 km/h,换算成转速作用于车轮。弹体受到推力作用,其余反作用力参照上述曲线施加。弹和炮在载车行驶稳定后发射,上装部分方位角0°~360°,文中以对载车影响最大的90°方位角为例,分别选择高低角0°、45°和60°,在倾斜5°的D级路面下进行仿真分析,结果如下。 图8所示为载车在导弹和火炮同时发射时绕x轴的滚转角,由图8中可以看出高低角为0°时载车滚转角较大,45°时次之,60°时变化最小,主要是因为随着高低角的增加,施加在动力学模型中的反作用力臂减小,导致滚转角减小。 图8 载车滚转角 由图8中可以看出在发射时刻战车受到反冲力,滚转角变化较大,相对于初始时刻的-5°分别变化了1.4°、2.6°和3.3°。 图9和图10所示为载车滚转角速度和角加速度变化曲线,发射前由于路面随机激励作用,有小幅度的变化,在发射过程中会有较大幅度的变化。 图9 载车滚转角速度 图10 载车滚转角加速度 表1中列出了角速度和角加速度的均方根值和最值。 表1 结果汇总 文中综合考虑防空系统行进间发射时所受的路面随机激励、导弹后坐力和燃气流冲击力、火炮反作用的影响,建立基于谐波叠加法原理的三维路面和弹炮结合防空武器系统动力学模型,并进行了行进间发射动力学仿真,主要对载车发射时刻的安全性和动态响应进行分析与研究。限于篇幅,只给出了D级路面下90°方位角发射这一较恶劣工况的仿真结果,分析表明,在规定路况和车速条件下发射时载车滚转角变化在3.3°左右,未见明显侧翻,可以安全发射;同时得到载车滚转角速度和角加速度的变化曲线,为车载雷达电机补偿提供参考依据。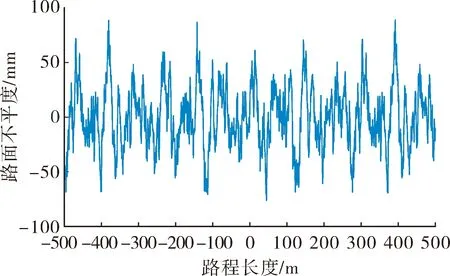
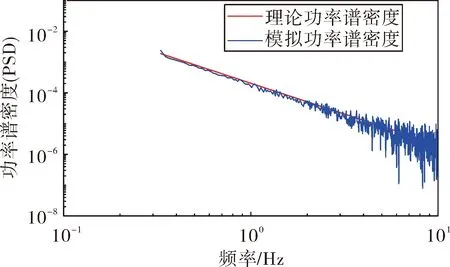
1.3 三维路面建立与验证

2 动力学仿真分析
2.1 动力学模型
2.2 施加载荷
2.3 轮胎模型
2.4 仿真分析与研究
3 结论
