非均匀湍流场中螺旋桨噪声研究*
2019-07-29蒲汲君周其斗吕晓军
蒲汲君,周其斗,吕晓军
(海军工程大学 船舶与海洋工程学院, 湖北 武汉 430033)
湍流中螺旋桨的低频宽谱辐射噪声一直都受到国外学者的关注和研究,但国内在这方面的研究还相对较少,在这些研究中一般都使用建立在FWH理论上的频谱法来分析旋转机械远场噪声问题。早在1975年,Amiet[1]理论推导了螺旋桨低频宽谱辐射噪声的公式,并将螺旋桨噪声谱与湍流积分尺度、湍流度、来流速度以及螺旋桨旋转速度等物理量联系在一起。
在研究螺旋桨的宽谱噪声时,一般只关心远场点的噪声问题,因此可假设螺旋桨桨叶沿弦长上是声源致密的(忽略螺旋桨弦长带来的影响)。Sevik[2]通过空间中任意两点的速度相关性建立了描述湍流场的数学模型,在假设螺旋桨盘面的湍流是各向同性之后,对湍流中螺旋桨宽谱噪声进行了理论推导并发展了预报该宽谱噪声的方法。另外,Sevik还在水洞中测量了十桨叶螺旋桨在湍流中的宽谱噪声。在Sevik研究的基础上,Martinez等[3]考虑了螺旋桨旋转带来的影响,较好地预报了叶频处的波峰现象。
随后,Minniti[4]、Mueller[5]等在风洞中测试了不同网格尺寸格栅后湍流积分尺度、湍流度等物理量,并对四叶螺旋桨进行了湍流中的噪声测试。在Sevik十桨叶螺旋桨研究的基础上,Wojno和Blake等[6]在风洞中对相同十桨叶螺旋桨进行了噪声测试,使用频谱法理论计算了相同条件下的螺旋桨噪声谱,但结果显示在一倍叶频下理论值与试验值相差较大。Anderson和Catlett等[7]使用相关性法对Wojno的十桨叶螺旋桨进行了理论计算,并与试验值进行了对比,结果显示频率在一倍叶频和三倍叶频之间时噪声预报效果较好。Glegg等[8]则以Wisda等[9]的十叶桨模型为研究对象,分别计算了螺旋桨在平板边界层湍流和细长圆柱后湍流的宽频辐射噪声,得到的噪声频谱曲线与试验值大致趋势保持一致,但叶频处的波峰值与试验值相比仍有较大差距。
国内对螺旋桨宽频噪声的研究起步较晚,但近些年也取得较大成果,其中具有代表性的是周其斗和蒲汲君[10-11],其中周其斗将George等[12]的频率谱和Corcos[13]的波数谱结合在一起,并在Amiet薄机翼理论的基础上计算了螺旋桨桨叶表面的压力脉动,再使用了平均流效果的格林函数,建立了湍流中螺旋桨宽频噪声预报理论。该理论并没有对螺旋桨叶片的弦长方向进行简化处理,而是采用了更为精确的对桨叶表面进行积分的方法。
1 螺旋桨宽频噪声理论研究
图1给出了湍流中螺旋桨噪声的计算流程。一般在试验中可测得螺旋桨盘面的湍流数据和远场的噪声谱,而理论推导中通过传递函数和格林函数同样可以计算出噪声谱的大小,在此之间一般可以先计算出螺旋桨的激振力宽谱,再根据计算得到的激振力宽谱最终得到螺旋桨的噪声谱。
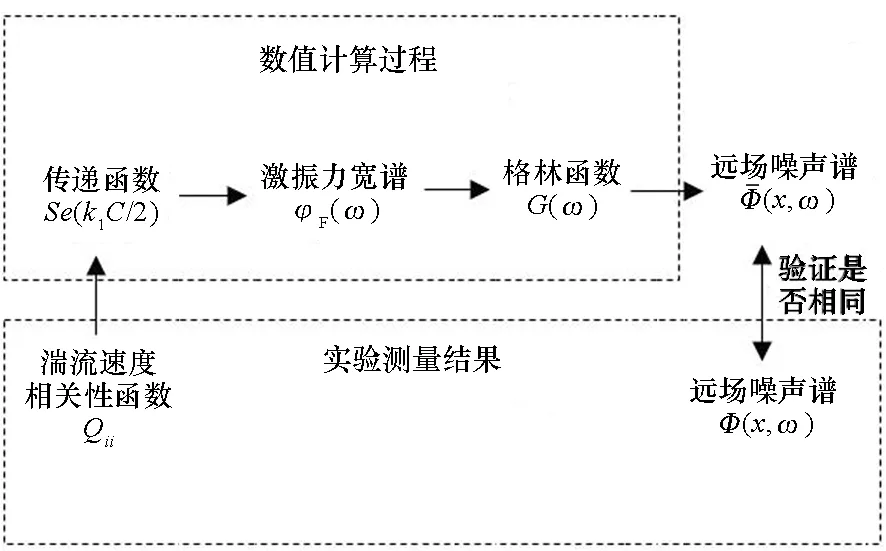
图1 螺旋桨湍流噪声计算流程Fig.1 Calculation process of propeller noise in turbulence
1.1 螺旋桨噪声公式推导
图2给出了螺旋桨的声偶极子模型示意图。湍流引起的螺旋桨辐射噪声声压p(x,T)一般可由简化得到的声偶极子数学模型得到,具体计算公式为:
(1)
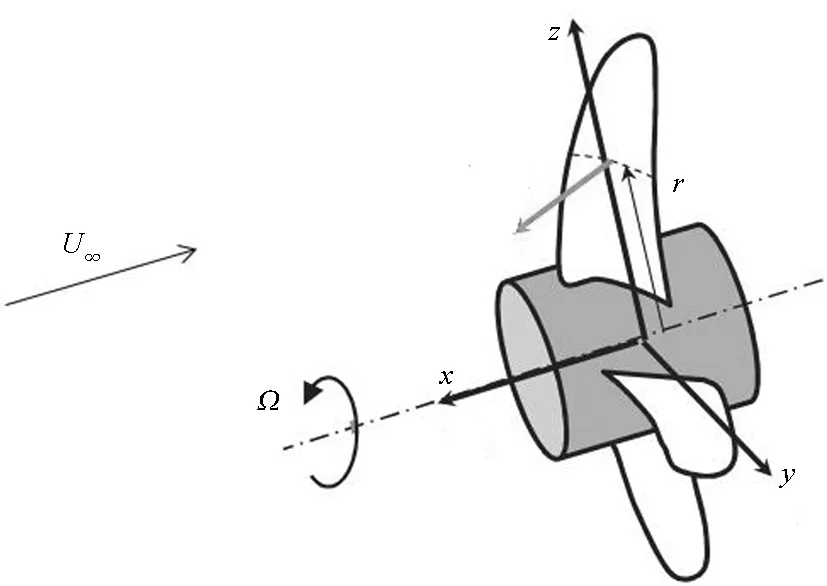
图2 螺旋桨偶极子模型Fig.2 Dipole model of propeller
其中:ps(ξ,t)为螺旋桨桨叶表面的压力,S(ξ)为螺旋桨上的任意积分单元;R为声源点y与场点x的距离,定义R=x-y(ξ,t);源点马赫数定义为M=(1/c)(d/dt)(y(ξ,t)),c为声速;ni为垂直于螺旋桨桨叶表面的单位坐标向量;te的表达式为te=T-(1/c)|x-y(ξ,te)|。
一般更关注远场噪声,因此,可以假设螺旋桨桨叶沿弦长上是声源致密的,该假设在声波波长远大于弦长(c/f≫C,f为频率)时是成立的。在该声源致密的假设下,延迟时间T-te沿弦长上的差异是可以忽略的,因此,沿弦长方向的压力积分可以使用合力L(r,t,S)来代替。于是,式(1)可以简化为:
(2)
式中,r为螺旋桨任意叶面积分单元的半径,N为螺旋桨叶片总数,S=0,1,2,…,N-1,Ri为场点与源点距离R的坐标分量。文献[7]指出,如果假设整个螺旋桨是致密声源,可以继续对式(2)进行简化。该假设一般要求满足两点:一是螺旋桨任意两相关联积分源上延迟时间的差异很小,不会引起声波上相位的巨大变化。为满足该假设,一般要求
max[R(r,S,te)-R′(r′,S′,te)]<εc/f
(3)
其中,ε为人为设定的衡量距离差异的临界值,文献[7]中取ε=0.125,并进行了验证。二是声源的尺寸相较于声波传播距离应足够小,当2rt<εc/f时该要求成立,rt为叶梢处的半径。在该假设下,式(2)做傅立叶转换后简化[7]为:

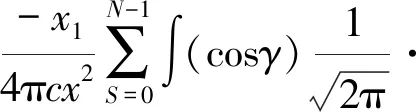
(4)
式中,xi为场点坐标分量,Ω为螺旋桨旋转速度,γ为螺距角,β(r)为螺旋桨侧斜角。于是,螺旋桨噪声宽谱的表达式如式(5)所示[7]。观察式(5)可以发现,Φ(x,ω)的大小由频率为ω、ω-Ω和ω+Ω的螺旋桨轴向激振力谱共同决定。
Φ(x,ω)=2E[p(x,ω)p*(x,ω)]
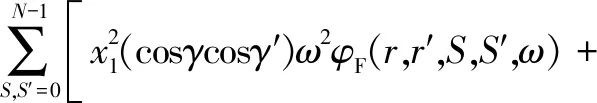
(5)
螺旋桨激振力φF(r,r′,S,S′,ω)的详细推导过程见下一节,这里只简要给出它的表达式:
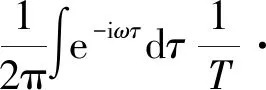
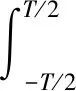
cosγcosγ′
(6)
1.2 螺旋桨激振力公式推导
1.2.1 各向同性湍流
相关性法最早由Sevik[2]提出,并与试验值进行了对比,图3给出了螺旋桨相关性法的原理示意。单片桨叶在半径r截面处受到的脉动压力如式(7)所示。
L(r,t,S)=ρπC(r)wN(S,r,ω)·U(r)
Se(k1C/2)(cosγ)e-iωt
(7)
其中,N为螺旋桨叶片总数,S=0,1,2,…,N-1。假设螺距角γ与来流入射角θ近似相等,可近似认为cosγ为升力方向的方向余弦,U(r)为来流相对速度,wN为叶片截面处垂直于桨叶表面的湍流脉动速度大小,C(r)为桨叶弦长,Se(k1C/2)为传递函数。
Se(k1C/2)函数的表达式如式(8)所示,这里κ为无因次波数,κ=k1C/2。
(8)
式中,H0和H1分别为0阶和1阶Hankel函数。由于Sear函数的表达式过于复杂,在计算时可以引用Liepmann[14]的近似结果,其表达式为:
(9)
假设螺旋桨盘面的湍流场是各向同性且均匀的,湍流速度场可由空间中任意两点的湍流速度相关性表示。将桨叶不同半径处的激振力相关性沿半径上做积分运算,再取傅立叶变换后可以得到螺旋桨激振力谱的表达式如式(6)所示。
将式(7)代入式(6),得到激振力谱的表达式如式(10)所示。
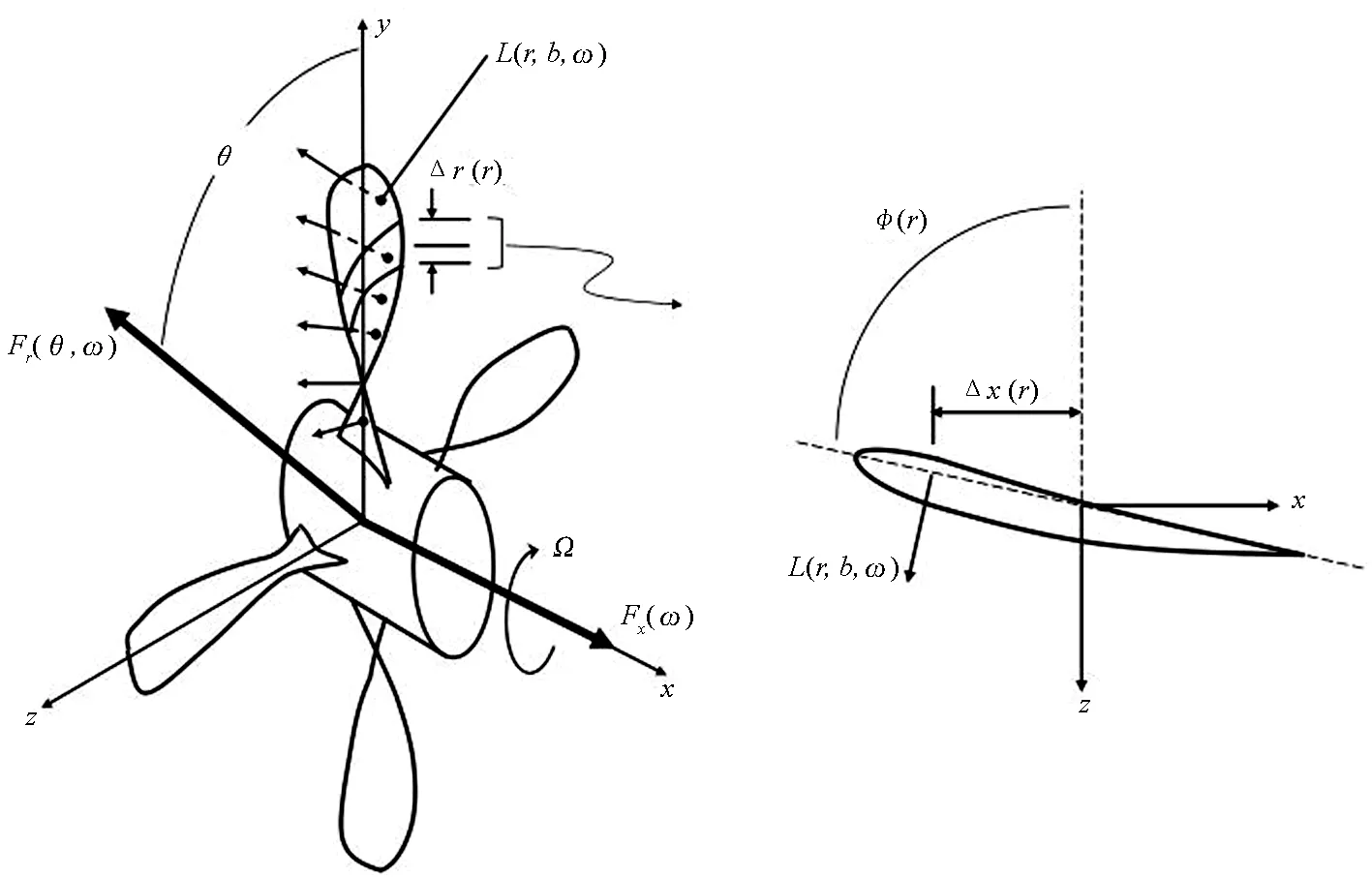
图3 湍流导致的激振力示意图Fig.3 Lift force induced by inflow turbulence
φF(r,r′,S,S′,ω)=π2ρ2cosγcosγ′·
(10)
QNN(r,r′,S,S′,τ)表达式如式(11)所示,其中ejN′(r′,2πS′/N+Ωτ+β(r′))和eiN(r,2πS/N+β(r))为桨叶表面垂直方向的方向余弦,wi为湍流速度w沿x,y,z方向的分量(i,j代表x,y,z)。
wj(r′,2πS′/N+Ω(τ+t)+β(r′)) ·
eiN(r,2πS/N+β(r))ejN′(r′,2πS′/N+Ωτ+β(r′))dt
=eiN(r,2πS/N+β(r))ejN′(r′,2πS′/N+Ωτ+β(r′))·
Qij(r,2πS/N,r′,2πS′/N+Ωτ+β(r′),τ)
(11)
前文中已提及,螺旋桨盘面的湍流场是各向同性且均匀的,此时空间中任意两点湍流速度的相关函数可用g(η)和f(η)表示,这里η为两点间距离。此时Qij的表达式为:
(12)
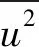
(13)
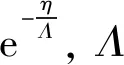
(14)
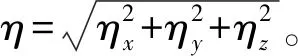
(15)
1.2.2 各向异性湍流
与各向同性湍流下公式相比,这里主要考虑桨叶旋转到不同位置时湍流积分尺度和湍流度的变化,并引入时间变量t,则:
L(r,t,S)=ρπC(r)wN(S,r,ω)·
U(r,t)Se(k1C/2)(cosγ)e-iωt
(16)
与前文均匀湍流中螺旋桨激振力的公式相同,这里的非均匀湍流速度场仍然可由任意两点的速度相关性表示。通过将不同半径处的激振力相关性沿半径方向进行积分运算,再取傅立叶变换后可以得到螺旋桨激振力谱的表达式如式(17)所示。
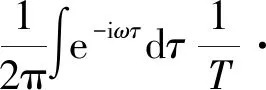
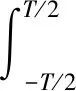
cosγcosγ′
(17)
将式(16)代入式(17),得到激振力谱的表达式为:
φF(r,r′,S,S′,ω)=π2ρ2U(r,t,S)U(r′,t+τ,S′)·
wi(r,2πS/N+Ωt+β(r),t)·
wj(r′,2πS′/N+Ω(t+τ)+β(r′),t+τ)·
C(r)C(r′)eiN(r,2πS/N+Ωt+β(r))·
ejN′(r′,2πS′/N+Ω(t+τ)+β(r′))·
(18)
这里t为绝对时间,τ为两点之间的相对时间,首先设定:
wj(r′,2πS′/N+Ω(t+τ)+β(r′),t+τ) ·
U(r,t,S)U(r′,t+τ,S′)eiN(r,2πS/N+Ωt+β(r))·
ejN′(r′,2πS′/N+Ω(t+τ)+β(r′))dt
(19)
这里f(r,r′,S,S′,τ)为包含时间t和τ的所有相关项,继续简化得到:
f(r,r′,S,S′,τ)=E[wN(r,2πS/N+Ωt+β(r),t)·
wN(r′,2πS′/N+Ω(t+τ)+β(r′),t+τ) ·
g(r,t,S)g(r′,t+τ,S′)]
其中,g(r,t,S)为关于来流速度U(r,t,S)的函数,g(r,t,S)的表达式为:
(20)
由于湍流函数w(r,2πS/N,t)与来流速度的相关函数g(r,t,S)之间相关性几乎为零,于是可近似认为:
f(r,r′,S,S′,τ)≈E[wN(r,2πS/N+Ωt+β(r),t)·
wN(r′,2πS′/N+Ω(t+τ)+β(r′),t+τ)]·
E[g(r,t,S)g(r′,t+τ,S′)]
(21)
式中,E为期望函数,这里将湍流速度和来流速度分别求期望,得到:
E[wN(r,2πS/N+Ωt+β(r′),t)·
wN(r′,2πS′/N+Ω(t+τ)+β(r′),t+τ)]
=Q(r,r′,S,S′,τ)
(22)
E[g(r,t,S)g(r′,t+τ,S′)]
=G(r,r′,S,S′,τ)
(23)
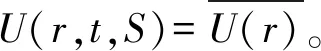
E[g(r,t,S)g(r′,t+τ,S′)]
(24)
本文研究的是各向异性湍流下螺旋桨噪声的计算,从文献[16]的研究中可以发现,多周期激流丝可产生非均匀湍流场。以四周期激流丝为例,如图4所示,在激流丝后会产生大量的涡旋,使得相关区域湍流的湍流度显著提高,这些不同尺度的湍流涡则导致了螺旋桨宽频噪声的产生。在其他位置湍流的湍流度则相对较小,因此螺旋桨盘面处的湍流是非均匀各向异性的。
将螺旋桨盘面的湍流域划分为8个区域,从图中观察发现:只有ACEG区域的湍流度较大,因此只有流经这些区域,桨叶叶片才能产生相对较大的噪声。另外值得注意的是,ACEG区域中任一区域与其他区域之间都相隔一个湍流度几乎为零的区域(BDFH),所以若桨叶单元位于ACEG中不同的两个区域,则它们之间湍流速度的相关性仍然为零;只有两桨叶单元同时位于ACEG中的任一相同区域时,它们之间湍流速度的相关性才不为零。湍流区域的角度可以任意设定,以后在试验中可以精确测量各种激流丝后的湍流场。
按照上文对湍流速度的分析,相关函数有如下定义:
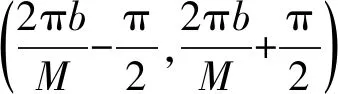
Qij(r,r′,S,S′,τ,t)
=Qij(r,2πS/N+β(r),r′,2πS′/N+Ωτ+β(r′),τ)
除此之外,
Qij(r,r′,S,S′,τ,t)=0
(25)
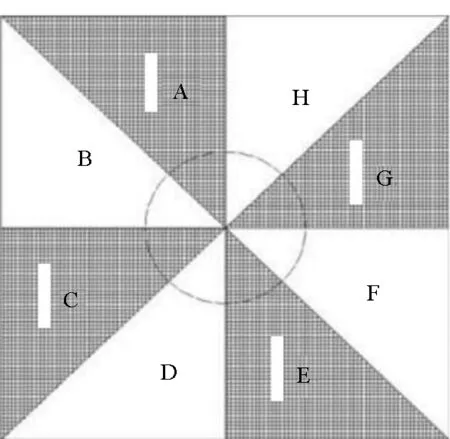
图4 安装在螺旋桨前的四周期激流丝示意图Fig.4 Four-cycle wake screen before propeller
2 均匀湍流下螺旋桨噪声计算
计算模型为Wojno等在Hessert中心的消声风洞中所测量的十叶螺旋桨,螺旋桨参数与Sevik十叶螺旋桨完全一致。螺旋桨无侧斜角,有十片桨叶,桨叶弦长恒定为25.42 mm,桨叶半径为10.16 cm,桨毂半径为2.5 cm,具体几何形状如图5所示。螺旋桨的转速为55 r/s,螺旋桨进速J为1.17,螺旋桨叶根处侧斜角为63°,叶梢处侧斜角为21°。螺旋桨前方网格尺寸为7.62 cm,网格金属丝直径为1.27 cm。
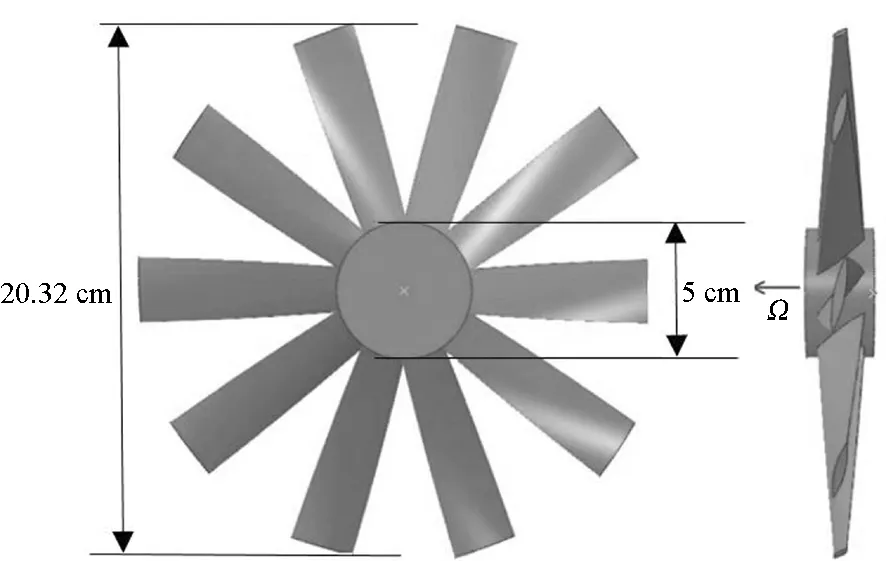
图5 螺旋桨几何图Fig.5 Geometry of the propeller
另外,Wojno等在风洞中还对螺旋桨盘面处任意两点之间湍流度的相关性进行了详细测量,经过分析,认为该湍流是均匀且各向同性的,其湍流度为6%。虽然Wojno等在文献中并没有提及湍流积分尺度的大小,但Paul和Uhlman[17]根据Wojno等的湍流速度测量数据,计算得到了湍流积分尺度Λ=0.023 m。 Wojno认为风洞中由湍流引起的螺旋桨激振力十分微弱,所以进行了远场的螺旋桨噪声的测试,螺旋桨测量点位置x如式(26)所示,其中建立的坐标系如图2所示,原点位于螺旋桨中心,x轴方向与螺旋桨轴向方向平行。
x=|x|cosBi+0j+|x|sinBk
(26)
式中,|x|= 0.91 m为测量点与坐标原点的距离,B= 45°为测量点的方位角。使用式(3)判断,认为该测量点的位置满足远场点的要求,因此使用式(5)的偶极子模型来预报该点噪声是合适的。后续都采用MATLAB软件自编程序进行研究计算。
图6给出了通过式(5)的偶极子模型计算得到的远场螺旋桨宽频噪声与Wojno在风洞中测得的试验值(图中f为频率,BPF为叶频)。由于Wojno测量得到的数据是由多点构成的,各个频率处的噪声谱大小并不明确,所以这里使用了这些数据点的上限与下限来表示试验值的具体范围。

图6 螺旋桨宽频噪声计算值与试验值比较Fig.6 Prediction of propeller broadband sound level compared to measurements
观察图6发现,宽频噪声的计算值在一倍叶频到和三倍叶频之间与Wojno试验值吻合较好,计算值准确预报了一倍叶频和两倍叶频处的波峰现象。但在一倍叶频之前,试验值下降得十分剧烈,而计算值的下降幅度较预报值较低。另外,试验值在靠近三倍叶频处,存在一个较为明显的上升现象,而计算值在该阶段呈平稳下降的趋势。关于这一点,Wojno认为在三倍叶频以后,螺旋桨噪声增加了新的噪声源,Wisda[9]认为该噪声源是由螺旋桨桨叶后缘扰动流经水流引起的,因此再使用式(5)的偶极子模型预报螺旋桨噪声是不合适的。总的来说,在三倍叶频以内使用理论方法预报螺旋桨宽频噪声谱是合适的。
3 非均匀湍流下螺旋桨噪声计算
为了弄清湍流场不均匀程度对螺旋桨噪声谱的影响,进行了非均匀湍流下螺旋桨宽频噪声的研究。使用格栅产生非均匀湍流,格栅的周期数M=1,湍流积分尺度Λ=0.023 m,湍流度为6%,湍流区域的弧度大小分别为π/3、π/6和π/9。螺旋桨的转速为55 r/s,螺旋桨进速J为1.17,测试点的位置与第2节中均匀湍流下参数设置相同。
计算结果如图7所示,可以发现,随着湍流区域角度的增大,螺旋桨噪声谱显著提高。这是由于螺旋桨桨叶在扫过这些区域时,会在湍流的作用下发出噪声,随着湍流区域的增大,桨叶在旋转一周中能产生噪声的时间越多,因此螺旋桨噪声谱越大。另外,各个湍流区域下螺旋桨宽频噪声波峰的位置并没有发生变化,依然位于叶频处。可以得出结论:湍流场的非均匀性并不会影响宽频噪声波峰的位置,其依然取决于叶频的大小。
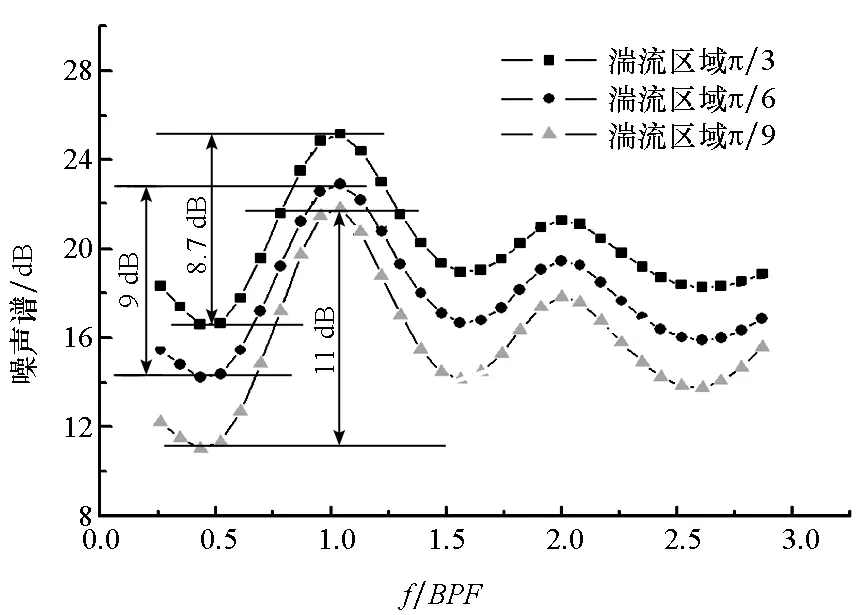
图7 不同角度湍流区域下螺旋桨宽频噪声Fig.7 Propeller broadband sound level under turbulence region of different angle
从图7还可以发现,随着湍流区域角度增大,螺旋桨噪声宽谱叶频处波峰的高度随之减小。分析认为,由于在假设中湍流区域与非湍流区域之间没有过度,桨叶在扫过该边界时,发出的噪声会发生剧烈突变,而湍流区域中的湍流场是均匀且各向同性的,随着湍流区域角度的增大,螺旋桨桨叶在该区域时间越长,也就意味着湍流场越均匀,因此湍流区域角度能够代表螺旋桨盘面湍流场的不均匀程度。通过以上分析可知,湍流区域角度越大,湍流场的不均匀程度越低,因此也可以得出结论:湍流场的不均匀程度越低,螺旋桨宽频噪声叶频处的波峰高度越低。
表1给出了湍流区域分别为π/3、π/6和π/9时噪声谱一倍和二倍叶频处波峰高度的具体值。从表中可以更清晰地观察到,湍流区域角度为π/6和π/9时叶频处波峰值差值分别为2 dB和0.9 dB,而湍流区域角度为π/6和π/3时叶频处波峰值差值分别为0.3 dB和0.5 dB,由此可以发现叶频处波峰值的差值并不随湍流区域角度的变化而线性变化,当湍流区域角度较小,也就是湍流场的非均匀程度很高时,对湍流场微小的改善也能起到较好的降低螺旋桨噪声的作用;当湍流场的非均匀程度较低时,想要从改善流场上降低螺旋桨噪声是很困难的。

表1 噪声谱叶频处波峰高度
为研究螺旋桨桨叶侧斜角度对噪声谱影响,进行一组除侧斜角度以外,其他参数都相同的螺旋桨在相同的湍流环境和工况下的计算。格栅的周期数M=1,湍流积分尺度Λ=0.023 m,湍流度为6%,湍流区域的角度为π/4。螺旋桨的转速为55 r/s,螺旋桨进速J为1.17,测试点的位置与第2节中均匀湍流下参数设置相同,螺旋桨侧斜角度分别为0、π/6、π/4和π/3。
图8给出了各侧斜角度下的螺旋桨噪声宽频谱。可以发现,随着桨叶侧斜角度增大,噪声谱在一倍叶频处的波峰值随之减小,但随着叶频数增大,侧斜角对叶频数波峰值的影响越发隐晦,原因可能是在程序中快速傅立叶变换的时间间隔取得较大。在二倍叶频处,侧斜角为0、π/6、π/4时,还保持着侧斜角越大,波峰值越小的规律,但侧斜角为π/3时的波峰值却较侧斜角为π/4时的波峰值大。总的来说,桨叶侧斜角会对湍流中螺旋桨发出的宽频噪声起到抑制作用,侧斜角越大,抑制作用越强。
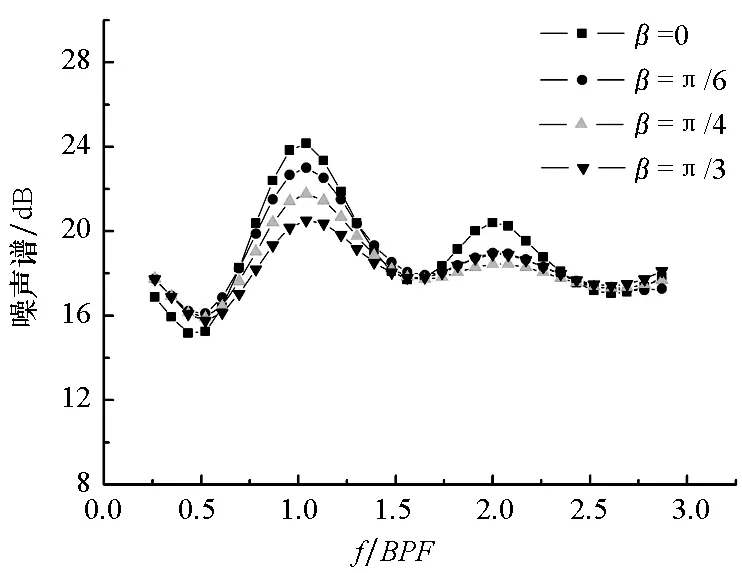
图8 各向异性湍流中各侧斜角度下噪声宽谱Fig.8 Sound spectrum of propeller under different skew angle in non-uniform turbulence
4 结论
本文介绍并推导了计算螺旋桨宽频噪声的相关性法,在此基础上推导了非均匀湍流下螺旋桨噪声的宽频公式。虽然本文并没有对激流丝产生的各向异性湍流场进行准确测量,只是进行了一定的假设和估计,但该计算对研究各向异性湍流场下螺旋桨宽频噪声的变化规律有一定的指导意义。
