马镇渗流井现场试验及数值模拟研究

45孙启明

(1.陕西地矿九0八水文地质工程地质大队，西安 710600； 2.陕西地矿集团有限公司 陕西省矿产资源勘查与 综合利用重点实验室，西安 710054； 3.中煤能源研究院有限责任公司 水文地质研究所，西安 710054; 4.长安大学 环境科学与工程学院，西安 710054； 5.长安大学 旱区地下水文与生态效应教育部重点实验室， 西安 710054； 6. 中圣环境科技发展有限公司 水文地质部，西安 710065)

1 研究背景

渗流井取水工程是将河水转化成地下水的新技术[1]。近年来，渗流井工程在水环境修复和地下水开发利用中的应用越来越多[2-3]。渗流井工程具有高产、低耗、高效、成本相对较低等优势。渗流井在集中供水[4]、控制地面沉降[5]、基坑降水[6]、尾矿坝排渗[7]及地下水和土体污染治理[8]中大量应用，取得了令人瞩目的成效。

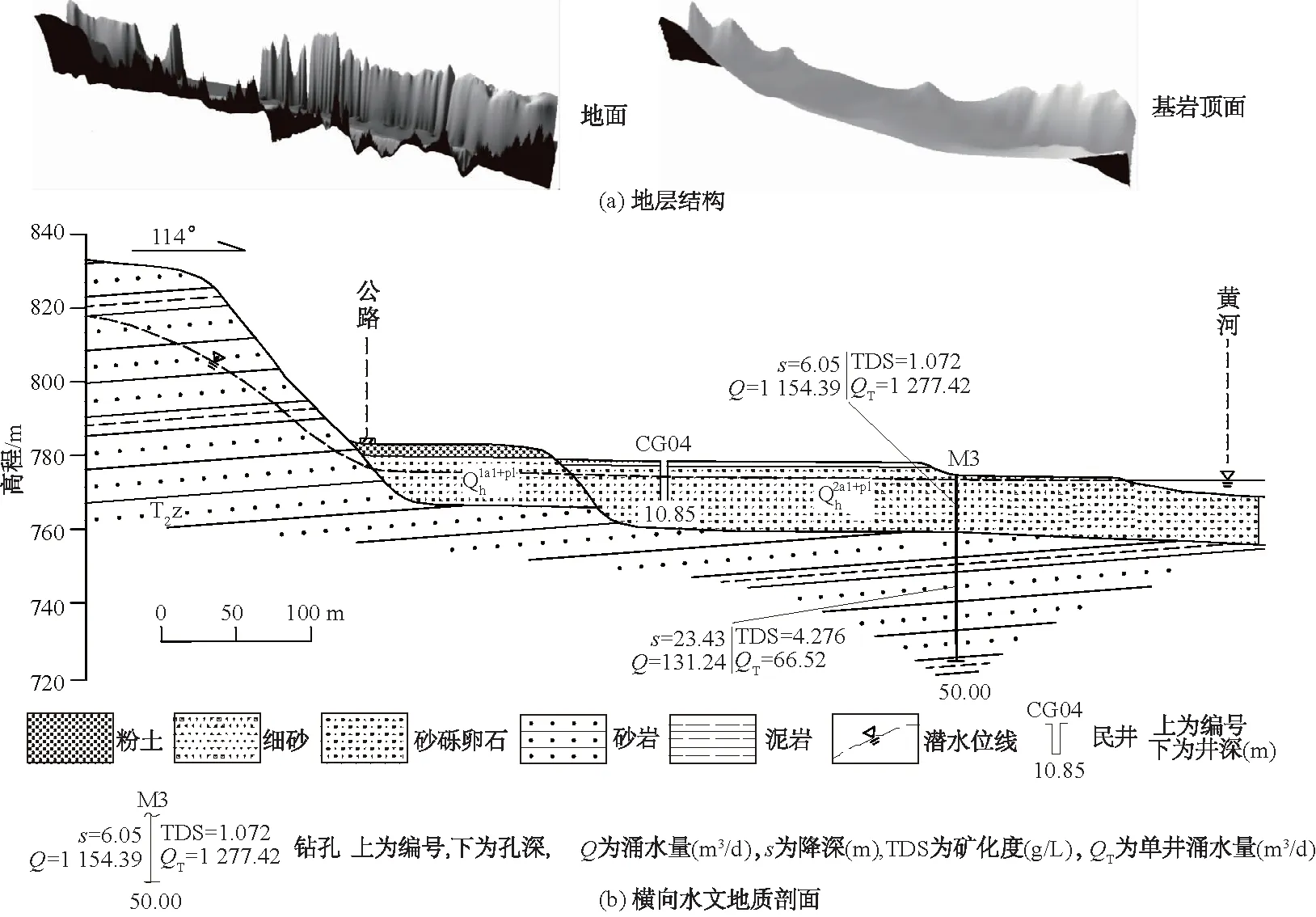
图1 地层结构及横向水文地质剖面Fig.1 Stratigraphic structure and transverse hydrogeological section

最早使用的计算模型多是在传统的井流公式基础上，根据各类非管井集水建筑物的特点，将非管井集水建筑物概化为相应的“井”，然后套用裘布依等井流公式得到相应的计算模型。1994年陈崇希等[9]对取水时井管中的水流流速与水头损失进行研究，从而提出“渗流-管流耦合模型”，并且通过实例对模型进行了验证。王玮等[10-11]基于“渗流-管流耦合模型”和“等效渗透系数”等理论，建立了渗流井取水计算模型，并成功将该计算模型用于渗流井取水方式下的悖牛川水源地地下水允许开采量计算。在已有的渗流井取水计算模型基础上，王玮等[12]以辐射管与含水层间交换水量为耦合点，进一步建立了改进渗流井取水计算模型，使得计算模型能够更精细地刻画辐射管的特征，并实现多个渗流井同时取水的计算。之后有不少学者[13-16]改进渗流井计算模型并成功应用在陕北多个以渗流井为取水工程的地下水资源评价中。

尽管渗流井取水工程取得了很大的成功，但现有的渗流井取水计算模型缺少实例工程验证。本文以渗流理论为指导，在分析大量渗流井工程结构、水文地质条件及取水效果的基础上，采用马镇实例工程现场抽水试验与计算机数值模拟相结合的研究方法，对渗流井取水效果进行研究；以“渗流-管流耦合模型”为前提，建立渗流井的取水计算模型，对渗流井结构进行优化设计，为渗流井取水方式的广泛应用和提高取水效率提供指导。

2 研究区概况

马镇位于神木县东部黄河沿岸，地处温带半干旱大陆性季风气候区，降水较少，冰冻期较长，黄河是区内的主要水系。研究区位于低山丘陵区和黄河谷地，丘陵区多为沟壑切割，起伏较大，整体坡度15°～40°，与河谷区多以岩质陡坡相接，陡坎高度10～30 m，局部达到40 m左右；河谷区地势平坦，研究区河谷平均宽度约750 m，高程782.0～786.7 m。

研究区地层由新至老分别为第四系全新统冲洪积砂砾卵石层、三叠系中统纸坊组砂泥岩不等厚互层。通过MALA地质雷达与钻孔资料相结合，进行控制性插值，可更加准确地描述地层结构。地层结构和横向水文地质剖面见图1。

3 数值模拟

在渗流井抽水试验基础上，考虑渗流井取水时辐射管内多种流态并存，以“渗流-管流耦合模型”为前提，并结合辐射孔-含水层间水量交换的计算方法，建立相应的三维数值模型。利用现场抽水试验结果对该模型进行识别和检验，验证渗流井取水计算模型的可靠性。

3.1 水文地质模型及数学模型

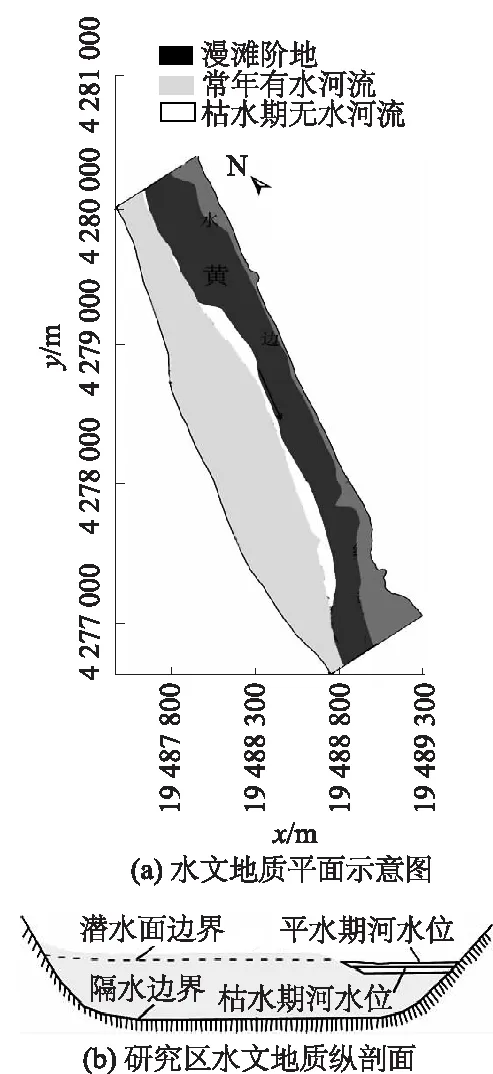
图2 模型概化Fig.2 Generalized model

研究区地下水主要接受农灌回归补给和大气降水入渗补给，主要以地表径流、蒸发及人工开采的方式排泄。在开采工程中，地下水主要接受河水渗漏补给。研究区东至黄河，开采地下水时，将激发河水补给地下水，故将黄河概化成河流边界。研究区西部以河谷区与丘陵区的分界线为边界，可将其概化为零流量边界；将黄河上下游概化为定水头边界,见图2(a)；研究区顶面概化成潜水面边界。研究区底面为基岩，概化为区域隔水底板，见图2(b)；渗流井抽水稳定时，竖井水位保持不变，将其概化为定水头边界。渗流井平面布置见图3。

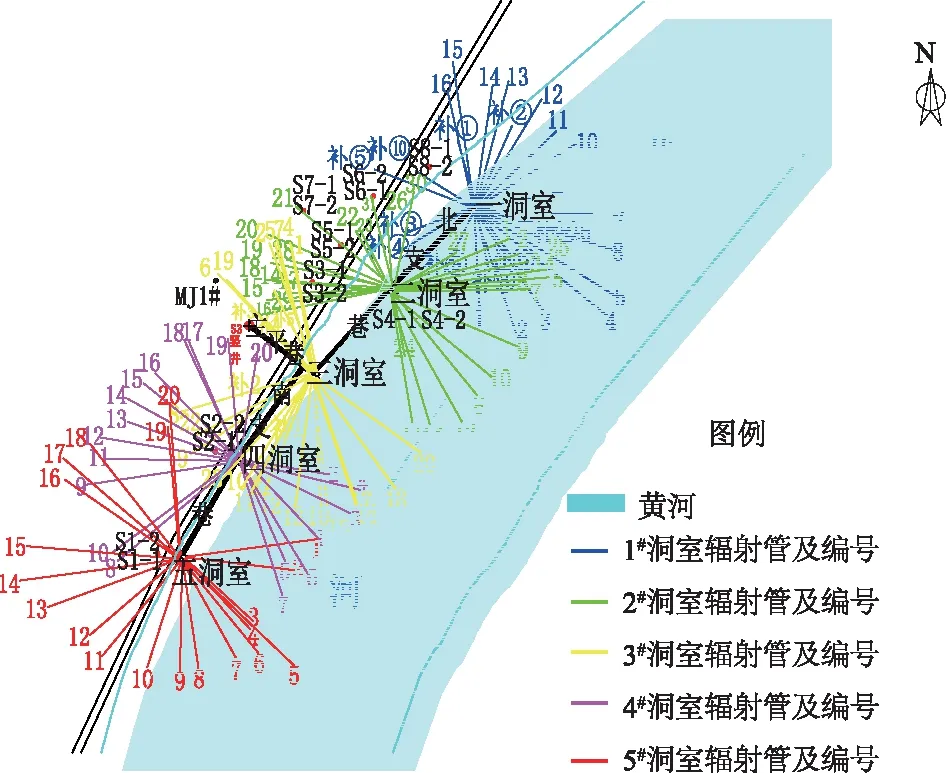
图3 渗流井平面布置Fig.3 Plan of seepage wells

渗流井取水时，地下水三维流特征显著，且水流服从达西定律。研究区数学模型如式(1)所示。

(1)

式中：K为渗透系数(m/d)；Hs为渗流井内动水位(m)；H为地下水位标高(m)；Hr为河流水位(m)；ΔH为水头损失(m)；Hp为井管内水位(m)；Qe为井管与含水层之间交换水量(m3/d)；Kr为河床介质垂向渗透系数(m/d)；Mr为河床介质厚度(m);Qp为井管内出水量(m3/d)；qr为河流与地下水交换水量(m3/d)；υ为水动力黏滞系数(m2/s)；ν为渗流速度(m/s)；Г2为第二类流量边界；np为潜水面内法线方向；n为二类边界外法线方向；C1为河流渗漏补给系数(m2/d)；C2为井管与含水层间的水量交换系数(m2/d);D为模拟区的范围；d为井管的直径(m)；g为水的重力加速度(m/s2)；e为井管管壁的粗糙度；l为水流路径长度;x,y,z为三维坐标系，xOy为水平面；xOz和yOz为垂直于水平面的两平面。

3.2 模型验证及降深等值线

本次模拟采用水平面二维规则正交网格有限差分法对马镇现场抽水试验进行模拟。首先对研究区进行20 m×20 m的等间距网格剖分，再对辐射孔、平巷及洞室位置处采用2 m×2 m局部等间距网格加密剖分。模型在水平方向(xOy)上分为376行、175列；在垂直水平面的另外两个面(xOz,yOz)上，考虑到采用常规的以实际含水层地层作为模型层剖分时不方便刻画辐射管，为了更好地刻画辐射孔，垂直方向上采用水平切片的方式剖分，将模型剖分成38层。模型网格如图4所示。

图4 模型网格Fig.4 Grids of the model

对抽水试验进行定降深的稳定流模拟，将3个试验段抽水试验结果与计算结果进行对比，见表1。

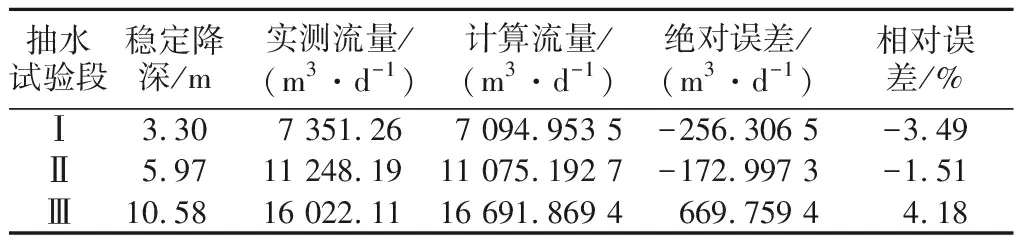
表1 实测流量与计算流量拟合结果Table 1 Result of fitting between measured flowand calculated flow

通过上述模型实测流量与计算流量对比，可以看出拟合的效果较好，满足模型的精度要求，故所建模型合理可靠。模型拟合后最终确定的水文地质参数如表2所示，研究区渗流井抽水试验前3个降深稳定后竖井横剖面降深等值线见图5。

表2 模型参数取值统计Table 2 Statistics of model parameters

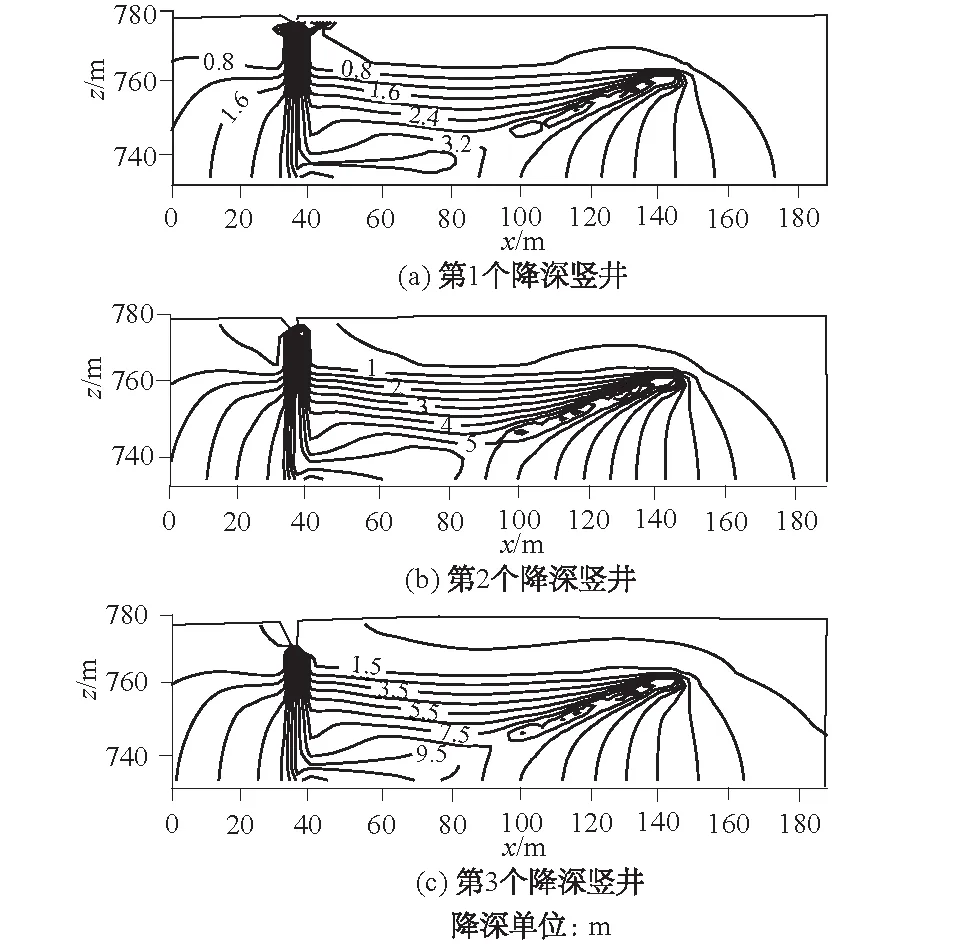
图5 3个降深竖井横剖面降深等值线Fig.5 Contours of water level drawdown of transversesections of three shafts

通过抽水试验稳定后竖井横剖面降深等值线图可以看出：在利用渗流井开采地下水时，整个渗流井周围形成降落漏斗，随着竖井降深的增加，渗流井附近的地下水水位降深也变大，渗流井影响面积也变大，且地下水水力坡度随之加大。

3.3 参数灵敏度分析

当需要定性或定量地评价参数的变化对模型结果带来的影响时，灵敏度分析是常用的方法[17]。本文以渗流井总出水量为基准，以改变参数后的渗流井出水量变化量为衡量模型参数灵敏度的指标。其公式为

Sk=∂y/∂xk≈{[y(xk+Δxk)-y(xk)]/y(xk)}/

(Δxk/xk) 。

(2)

式中：Sk为参数xk的灵敏度系数；y，xk分别是模型的因变量和自变量；Δxk为模型自变量的增量。其中：0≤|Sk|<0.05为不灵敏系数；0.05≤|Sk|<0.2为弱灵敏度系数；0.2≤|Sk|<1为中灵敏度系数；|Sk|≥1为高灵敏度系数。灵敏度分析结果见图6。

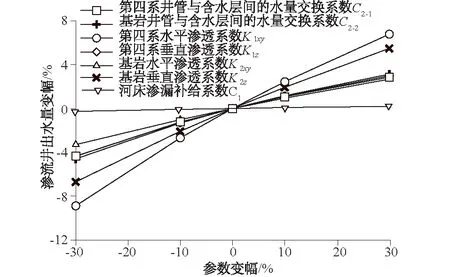
图6 灵敏度分析结果Fig.6 Result of sensitivity analysis

由图6可知，当改变第四系水平渗透系数K1xy时，渗流井出水量变化最大，改变河流渗漏补给系数C1值时，渗流井出水量变化最小。可见，各模型参数对渗流井出水量的影响由大到小依次为：第四系水平渗透系数K1xy>基岩垂直渗透系数K2z>基岩井管与含水层间水量交换系数C2-2>第四系垂直渗透系数K1z>第四系井管与含水层间水量交换系数C2-1>基岩水平渗透系数K2xy>河流渗漏补给系数C1值。由于基岩地层中辐射管长度较长，且布设有未加过滤设施的辐射孔，故对渗流井出水量影响也较大。表3为灵敏度系数计算结果。

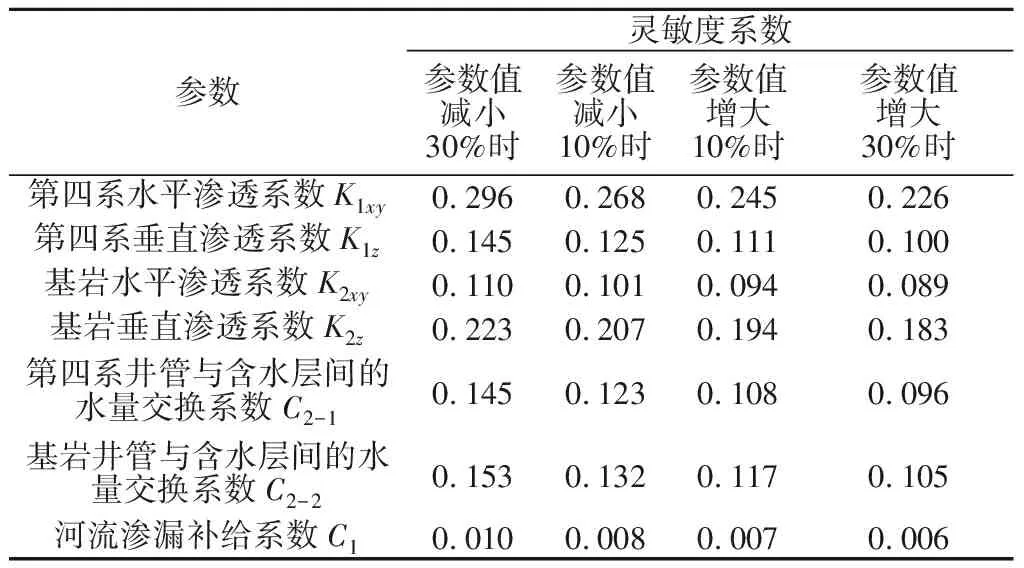
表3 灵敏度系数计算结果Table 3 Calculated values of sensitivity coefficient

由表3可知，模型参数灵敏度系数由大到小依次为：|SK1xy|>|SK2z|>|SC2-2|>|SK1z|>|SC2-1|>|SK2xy|>|SC1|。第四系水平渗透系数K1xy和基岩垂直渗透系数K2z为中等灵敏系数；井管与含水层间水量交换系数C2-1和C2-2、第四系垂直渗透系数K1z和基岩水平渗透系数K2xy为弱灵敏系数；河流渗漏补给系数C1值为不灵敏系数。通过表3中灵敏度系数同样可以看出，渗流井出水量与各参数呈正相关，这与上述分析相吻合。

图7 3种河流渗漏补给系数C1值在9种不同仰角条件下渗流井出水量变化Fig.7 Changes in the yield of seepage wells withnine different angles of altitude of radiant tubes inthe presence of varied conductance of river

4 渗流井结构优化设计

4.1 不同仰角辐射管方案优化

建立一个1口1个洞室的渗流井新模型，模型参数不变，该洞室上连接3根辐射管，在保证辐射管进入第四系含水层长度(1 m)不变的条件下，分别设计各辐射管仰角为15°，20°，25°，30°，40°，45°，50°，55°，60°，并在每种辐射管仰角方案的基础上设计3种河流渗漏补给系数C1值方案，相互组合共设计了27种方案。各方案渗流井出水量见图7。

由图7可以看出，随着辐射管仰角的增大，渗流井出水量先减小后基本趋于稳定，辐射管仰角在10°～20°之间时渗流井出水量减小不大，仰角在20°～30°之间时渗流井出水量减小较多；河流渗漏补给系数C1值放大10倍对渗流井出水量影响不大，但是河流渗漏补给系数C1值缩小10倍时，渗流井出水量减小较多。在保证辐射管进入第四系长度相等的条件下，辐射管仰角过小，施工成本和施工难度会增加。因此，辐射管仰角设置在20°～30°之间时渗流井取水效果较好。

4.2 不同洞室间距方案优化

利用4.1节中建立的模型，在保证渗流井取水段总长不变的条件下，分别设计7个洞室间距为50 m、5个洞室间距为75 m、4个洞室间距为100 m和3个洞室间距为150 m的4种方案，在每种洞室方案的基础上设计3种不同河流渗漏补给系数方案，相互组合共设计了12种方案，分析洞室间距对渗流井出水量的影响。设置抽水降深为5 m，渗流井多洞室出水总量及单个洞室平均出水量见图8。

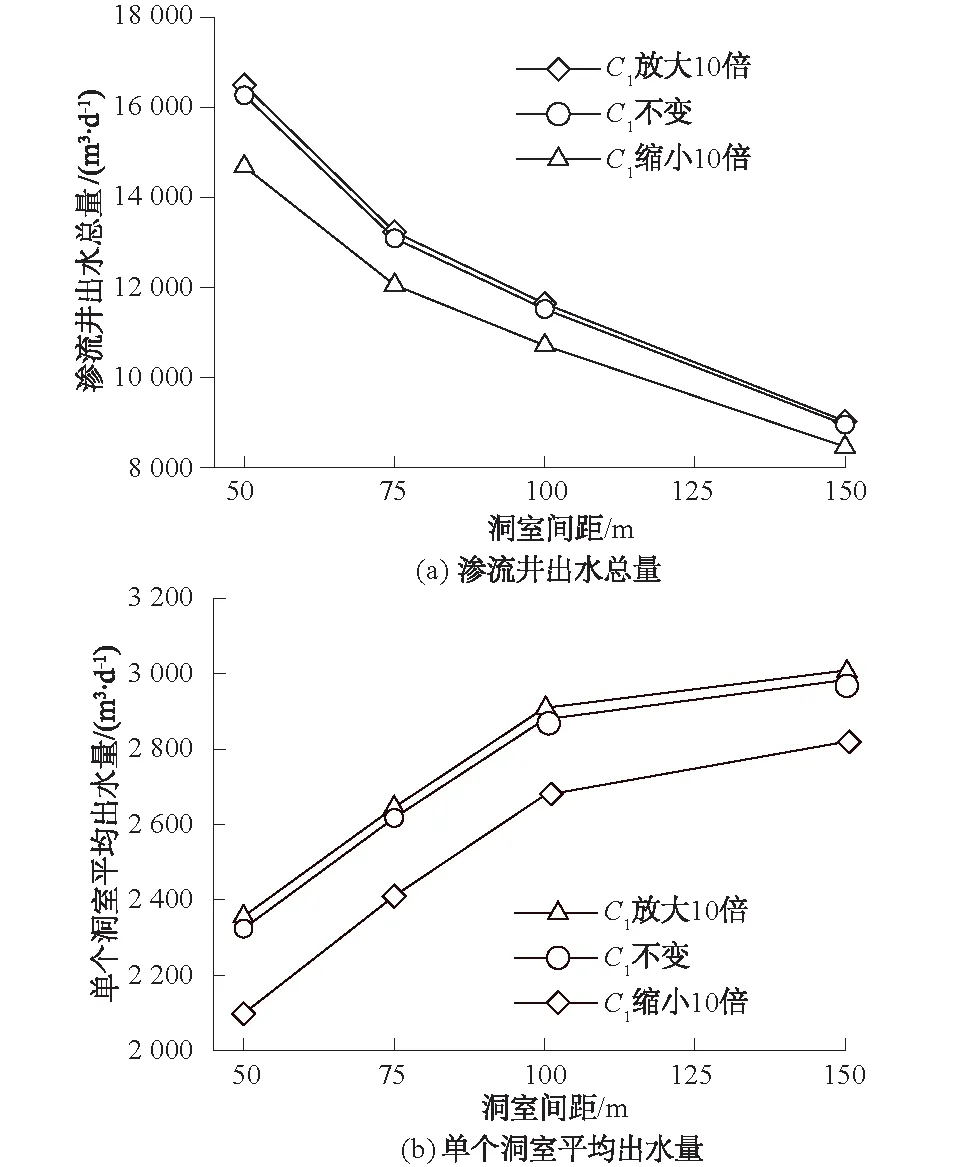
图8 渗流井出水总量和单个洞室的渗流井平均出水量随洞室间距变化曲线Fig.8 Curves of the total water yield of seepage wellsand the average water yield of single chamber againstchamber spacing

由图8可知，随着洞室间距的增大，渗流井出水总量不断减小，但是单个洞室渗流井平均出水量不断增大。洞室间距在50～75 m之间时，渗流井出水总量减小幅度较大，洞室间距在75～100 m之间时，渗流井出水总量减小幅度变小，且洞室间距在50～100 m之间单个洞室平均出水量增幅一致。洞室间距小，辐射管相互影响，导致单个洞室平均出水量小，且洞室间距小个数多，成本较高。故综合考虑成本和出水效率，洞室间距应设置在75～100 m之间。

5 结 论

(1)本文在充分了解研究区的自然地理、地质地貌以及地层岩性概况的前提下，使用地质雷达并结合钻孔资料获取地层情况，建立研究区的三维地层模型，结合水文地质条件资料，对研究区的边界进行概化，从而建立研究区水文地质数值模型。利用现场试验资料，对实际抽水量进行拟合，拟合结果良好，说明所建模型合理可靠，可以用来模拟该实际渗流井工程。

(2)对模型各参数进行灵敏度分析，得到对渗流井取水结果影响由大到小的模型参数依次为：第四系水平渗透系数K1xy、基岩垂直渗透系数K2z、基岩井管与含水层间水量交换系数C2-2、第四系垂直渗透系数K1z、第四系井管与含水层间水量交换系数C2-1、基岩水平渗透系数K2xy、河流渗漏补给系数C1值。在以后野外的水文地质勘探过程中，应尽量保证参数的精度和准确度，从而减小参数的不确定性给渗流井取水工程带来的不利影响。

(3)在合理的模型基础上，对马镇渗流井结构进行优化设计，优选出适合马镇地区的渗流井结构。辐射管仰角在20°～30°之间、洞室间距应设置在75～100 m之间，渗流井取水效果较好；河流的补给能力较好时，对渗流井出水量影响不大，而河流的补给能力较弱时，严重影响渗流井出水量。渗流井结构优化设计对提高渗流井取水效率有重要的指导意义。