复杂应力状态下Schmid因子
2019-07-29徐士东武保林王大鹏
徐士东,武保林,王大鹏
(沈阳航空航天大学 材料科学与工程学院, 沈阳 110136)
Schmid因子是研究金属变形机制的重要工具[1-2]。由于镁合金材料是密排六方不对称结构,Schmid因子的计算变得更加有意义。本文计算了镁合金各滑移系和孪生在轧制变形时的Schmid因子变化,其结果具有一定理论指导意义。
1 Schmid计算过程
在复杂应力状态下,分切应力表达式为
τ=Scosλ
(1)

1.1 全应力计算

图1 斜切微分面上的应力
那么全应力S在3个坐标轴上的分量S1、S2、S3分别为
(2)
而全应力计算公式为
(3)
1.2 切应力计算
为了方便计算,根据文献[3-4],将镁合金的四坐标密勒指数转化为三维直角坐标的密勒指数。此外,镁合金内的各晶粒取向不一致,所以晶体坐标系与外力坐标系的方向是不固定的。通过Bunge旋转法[5],得到二者对应关系为(ijk)T=G(g1g2g3)T,其中G为晶体取向矩阵,i、j、k为晶体坐标系单位基矢,g1、g2、g3为外力坐标系单位基矢。
复杂应力状态下,切应力计算可以表述为[6]
τ=∑i=1,2,3∑1,2,3mijσij
(4)
其中,σij和mij分别为应力矩阵A第i行、第j列的应力及其对应的Schmid因子。
单轴Schmid因子计算为[3,6]
(5)
其中,mii和mij分别为正应力和切应力的Schmid因子;η为滑移面或孪生面的单位倒易矢量;n0为滑移方向或孪生切变方向单位矢量。
通过式(4)和式(5),可以实现空间中任意取向的切应力计算。
1.3 轧制状态应力分析
假设轧制变形是均匀变形,每个晶粒受力与轧制应力相同,则每个晶粒受力为A,其中
假设轧件和轧辊完全滑动,再根据文献[7]推导,各向应力表达式为
(6)
其中,μ为轧件与轧辊摩擦系数;K为金属变形抗力;nσ可以根据希尔公式(式(7))来确定
(7)
上述过程为轧制应力状态Schmid因子的计算。Schmid因子受晶体取向、外加应力等影响。
2 结果分析
2.1 轧制状态下Schmid因子分析
对于镁合金来说,其室温变形机制主要是基面滑移和拉伸孪生。室温下,其临界分切应力满足CRSS基面≤CRSS拉伸≤CRSS柱面≤CRSS锥面[8]。在一些特定小应变时,基面滑移的临界分切应力比拉伸孪生的低很多[9-11]。
图2为(0001)[11-20]基面滑移系、(0-110)[-2-110]柱面滑移系和(2-1-12)[-2113]锥面滑移系的Schmid因子分布。(0001)[11-20]基面滑移的Schmid因子(图2a所示)取值范围在[0,0.5]内,当φ大于80°或小于15°时,在0.2以下。在欧拉角为(85.5°,45°,65°)时,Schmid因子取得最大0.4925。(0-110)[-2110]柱面滑移的Schmid因子(见图2b)随着φ的增大而增大,在欧拉角为(10°,90°,75°)时,取得最大Schmid因子 0.4827。(2-1-12)[-2113]的锥面滑移系的Schmid分布,见图2c。φ贴近在0°或者90°范围时,Schmid因子更大,基本呈现出Schmid因子随φ的增加先增加再减小的趋势。
结合室温下临界分切应力,基面滑移系开动比较容易,开动范围也很宽;柱面滑移和锥面滑移,在室温下不易启动。但一些特定条件下,柱面滑移和锥面滑移在室温下也可以启动[12-13]。影响柱面滑移系和锥面滑移系启动的主要因素是温度。当温度达到498 K时,锥面滑移和柱面滑移可以通过热激活开动[14]。
(-1012)[10-11]拉伸孪生(见图3a)的Schmid因子随着φ的增大而增大。在φ小于30°时,Schmid因子小于0,孪生不能启动。(0-111)[0-112]压缩孪生的Schmid因子分布(见图3b)随着φ的增大而减小,在φ大于75°时,Schmid因子小于0,孪生不能被激活。
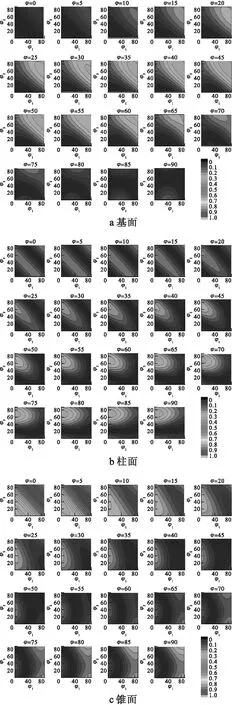
图2 滑移系的Schmid因子分布

图3 孪生Scchmid因子分布
拉伸孪生的临界分切应力很小,启动比较容易。而拉伸孪生产生的条件是平行于C轴方向受拉或垂直于C轴方向受压,在塑性变形中易被激活。在变形初期发生,拉伸孪生的启动可以改变原有的晶体取向,利于位错滑移和其余孪生的启动[15-16]。压缩孪生的临界切应力过高而不易启动,主要形成于变形后期,可产生局部变形并引发断裂源。Koike等人[17]发现AZ31镁合金在未达到疲劳极限之前,已经出现拉伸孪生,并表明断裂和压缩孪生有关。
2.2 压下量对Schmid因子的影响
压下量对轧制变形能力的影响非常重要。图4为热轧后退火的AZ31镁合金纵截面极图和φ=85°的ODF图,可以看出AZ31镁合金具有很强的基面织构,织构极密度最大在欧拉角为(0°,85°,0°)取得。对应于轧制的应力状态的坐标系,其取向为(0°,5°,0°)。为了计算方便,取欧拉角为(0°,0°,0°),研究不同滑移系的Schmid因子压下量的关系。
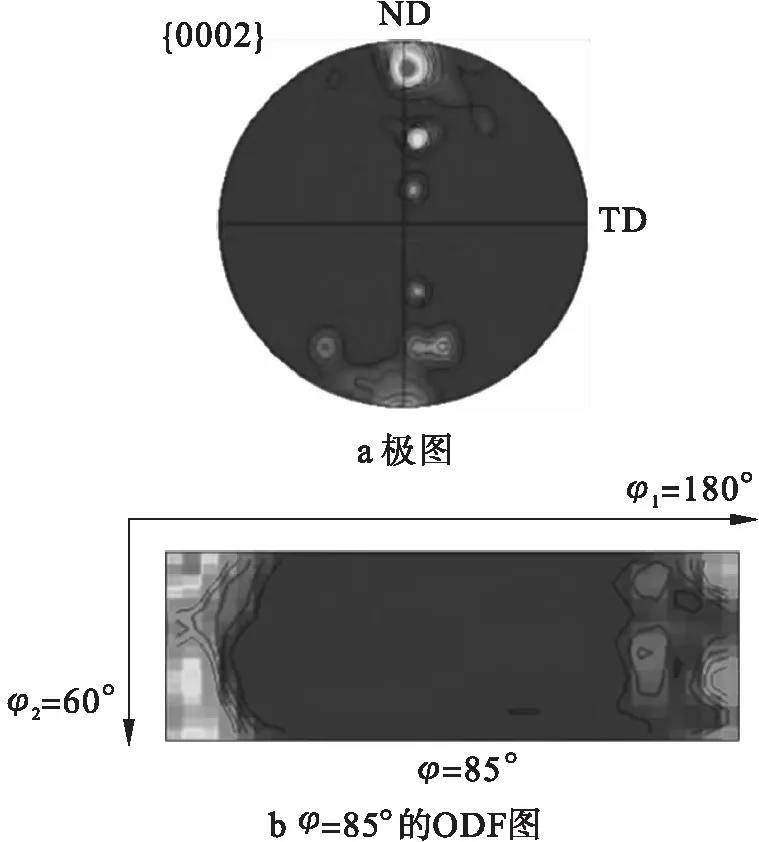
图4 热轧后退火AZ31镁合金织构图
图5是欧拉角为(0°,0°,0°)时,不同变形系的Schmid因子随压下量变化曲线。该方向晶粒的基面滑移系和(10-10)[-12-10]柱面滑移系的Schmid因子基本不受压下量的影响,(0001)[1-210]和(10-10)[-12-10]的Schmid因子始终为0,其余变形系的Schmid因子均随压下量的减小而增加。单纯考虑Schmid因子的角度分析,除(0001)[1-210]和(10-10)[-12-10]外,其余变形系都可以通过减小压下量来激活,因此,减小压下量可以提高镁合金轧制的变形能力。
3 结论
(1)给出了轧制应力状态的Schmid因子计算过程,为镁合金轧制变形机制的研究,提供理论依据。
(2)不同变形系的Schmid因子在欧拉空间中的分布不同。基面滑移在欧拉角接近45°时,Schmid因子最大。而柱面滑移系和拉伸孪生随着欧拉角φ的增加而增加,压缩孪生与之相反。锥面滑移的Schmid因子随着φ的增加,呈现先减小在增加的趋势。减小压下量可以提高镁合金轧制变形能力。
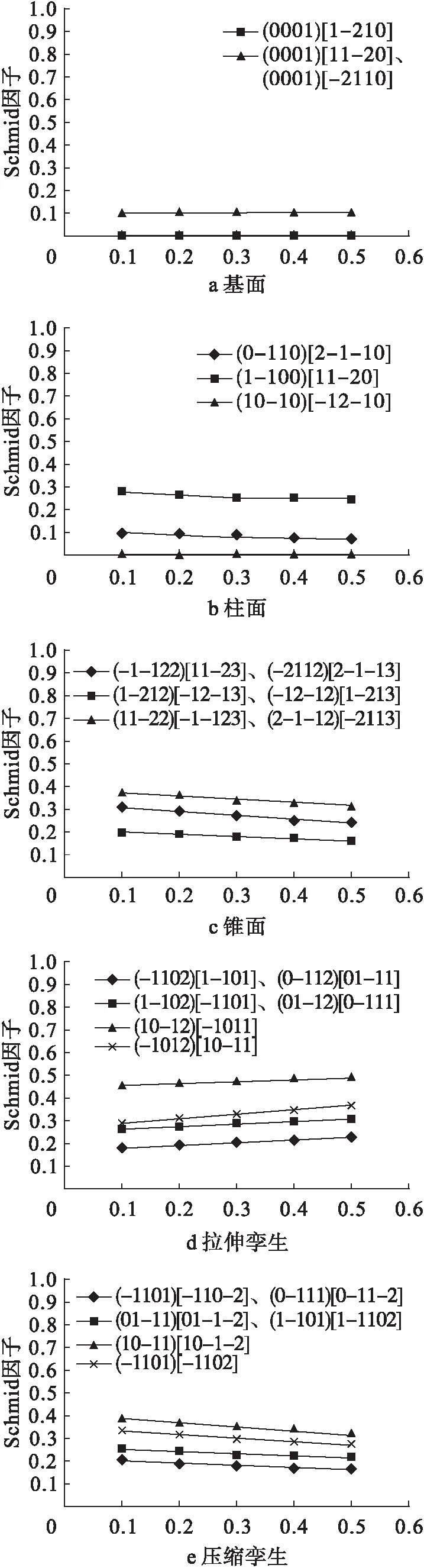
图5 不同变形系随压下量变化曲线
(3)对于具有基面织构的镁合金来说,减小压下量,可以使基面晶粒的大部分变形系的Schmid因子提高,只对基面滑移和(10-10)[-12-10]柱面滑移基本无影响。
