基于python的弓网仿真研究

陈宇昊

(中国铁道科学研究院 研究生部, 北京 100081)

受电弓系统和接触网系统是两个相对独立的系统，通过受电弓的碳滑板与接触线相接触，从而结合成一个整体。在列车的高速运动中，受电弓和接触线在水平方向、竖直方向和横向都有相对位移，因此对其受力分析较难。

1 弓网系统的动力学模型

我们通过对模型的简化，把水平向和横向看作列车匀速直线运动，由此只用考虑系统在竖直方向的相对位移，而两者的连接部分可以视为一个弹簧，其刚度为Ks，两者的耦合模型如图1所示：

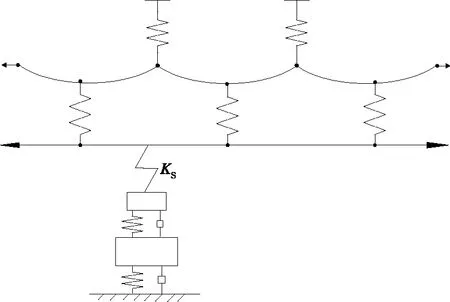
图1 弓网耦合模型图

1.1 受电弓模型

此二元受电弓模型的动力学平衡方程可以表示为：

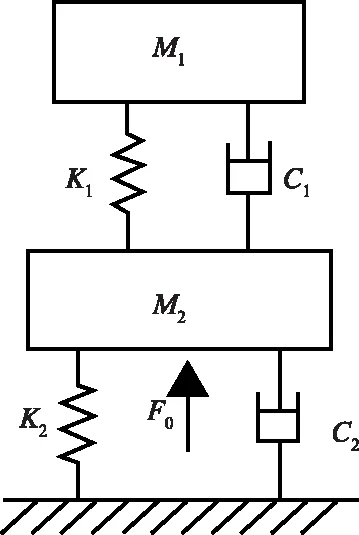
图2 受电弓二元质量模型

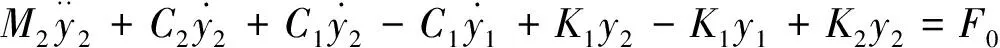
上式中：M1和M2分别是受电弓弓头和上下框架的等效质量；

K1，C1分别为受电弓弓头和上框架之间的等效刚度和阻尼；

K2，C2分别为是上框架和下框架之间的等效刚度和阻尼；

y1，y2是弓头和框架整体的位移；

F0表示受电弓静态时的抬升力；F(t)是受电弓碳滑板随时间变化的接触压力。

本研究中ALDH2基因Glu487Lys多态性分布情况：OSAHS组G/G、G/A和A/A频率分布分别为61.54%（128/208）、26.92%（56/208）和11.54%（24/208），对照组为65.49%（74/113）、25.66%（29/113）和8.85%（10/113）；OSAHS组和对照组比较，ALDH2各基因型多态性差异无统计学意义（P均＞0.05）。见表2。

1.2 接触网动力学模型

对于接触网的动力学仿真，主要考虑其承力索、接触线、吊弦定位器和支撑杆这些主要组成部分。模型如图3所示，承力索和接触线两端均施加张力补偿，分别用Tc和TJ表示；mpi和mDk分别表示的是吊弦的分布质量和定位器的等效质量；Kpi和kTA分别表示吊弦的等效刚度和定位器的等效刚度。

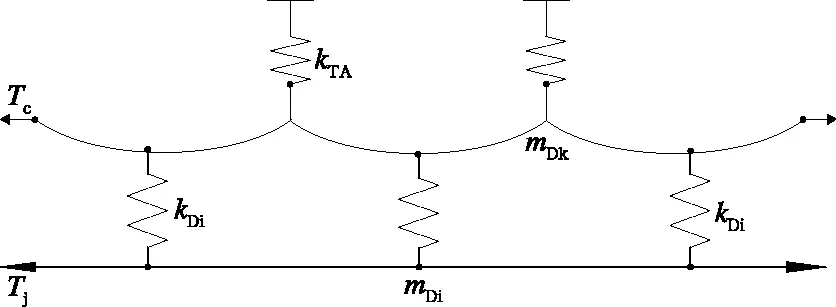
图3 接触网模型图

根据文献[1]，承力索和接触线的位移可以表示为：

其中，Cm为承力索的第m项幅值，Jm为接触线第m项的幅值；x为X轴向坐标；L为锚段总长度。理论上，m是从零到无限大，但是因为高阶项振动带来的影响极小，接触网的振动主要是集中在低阶部分，所以我们在模拟计算时只需要对于低阶项进行考虑即可。

1.3 弓网系统的运动方程

采用第2类拉格朗日方程从而推导弓网系统的运动方程。

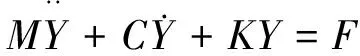
(1)

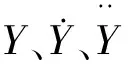
2 弓网耦合方程的求解

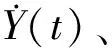
对于不同的逐步积分法适用的情况也不相同，对于这类的数值计算问题，一般采用到的逐步积分法有：分段解析法、中心差分法、Newmark-β法和Wilson-θ法。对于逐步积分法的选区，有以下几点：①收敛性，当离散时间步长Δt→0时，数值是否收敛于精确值；②计算精度；③稳定性：随着计算时间步数的增加，数值解是否变得无穷大(远离精确解)；④计算效率：需要花费较少的计算时间。

所以我们要寻找的是必须收敛、有足够的精确度、较高的稳定性和较高的计算效率的方法。通常采用的方法是Newmark-β法和Wilson-θ法。此两种方法原理比较类似，文中采用Newmark-β法进行展开介绍以及编程计算。

3 利用Python中开源库求解分析

仿真程序是利用Python编程语言编写的，借助Python强大的开源库；主要利用了NumPy和Matplotlib库。

其中NumPy库是一个开源的对于Python语言扩展的计算系统；它的强大之处在于：能对大矩阵，多维甚至N维向量进行处理。而Matplotlib是Python中的一个用来绘制二维图表的绘图库；其强大之处在于它可以仅仅使用几行代码实行复杂图表的绘制。

图4是基于PyCharm的Python语言的集成开发环境，图5是在程序运行之后输入初始的静态接触压力和列车速度窗口。

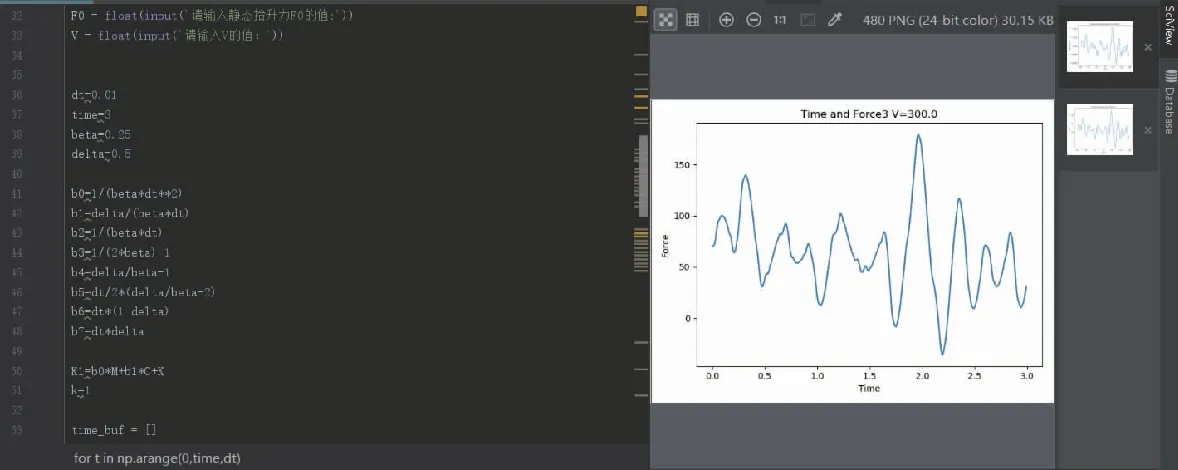
图4 Python语言开发环境

图5 数据输入窗口

此仿真研究了在不同速度下的接触压力的变化，如图6所示。

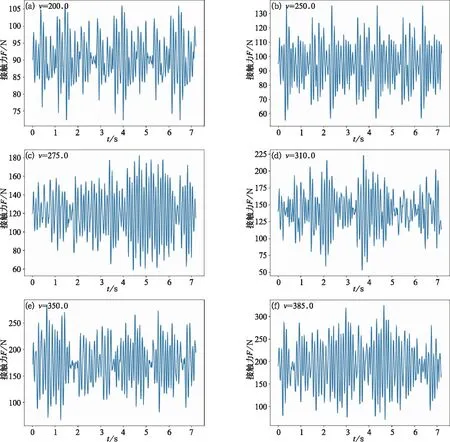
图6 不同速度下接触压力变化图

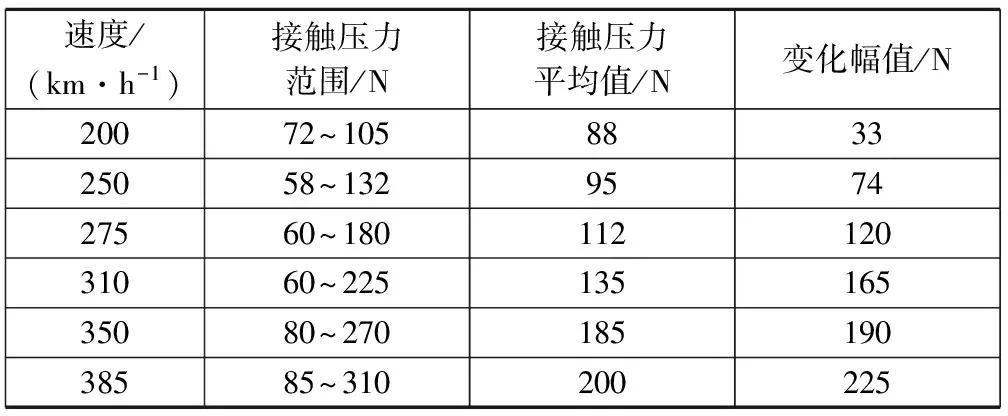
表1 不同速度下接触压力的变化表

4 弓网受流性能评价以及实际测试数据

依据TB 10761-2013《高速铁路工程动态验收技术规范》第8.2.2条款规定：对于弓网的动态接触压力的要求如下：

弓网动态接触力测试按一个跨距为一个分析单位，分析参数有：最大值、最小值、平均值、标准偏差。各参数评判标准如下：(1)最大值(N)：Fmax≤Fm+3σ；(2)最小值(N)：Fmin≥20；(3)平均值(N)：Fm≤0.000 97v2+70，(4)标准偏差(N)：σ≤0.3×Fm。

主要采用的是在2018年完成的京津城际铁路提速试验中的数据作为参考依据。京津城际铁路接触网采用全补偿简单链型悬挂，结构高度一般为1 600 mm，导线高度为5 300 mm，站线接触悬挂采用BzII70+Ris120(15 kN+15 kN)；正线接触悬挂采用BzII120+Rim120(21 kN+27 kN)。即承力索的张力为21 kN，接触线的张力为27 kN。

采用综合检测列车，对京津城际铁路进行测试，其受电弓型号均为DSA380，静态抬升力为70 N。测试结果如图10和表2所示。

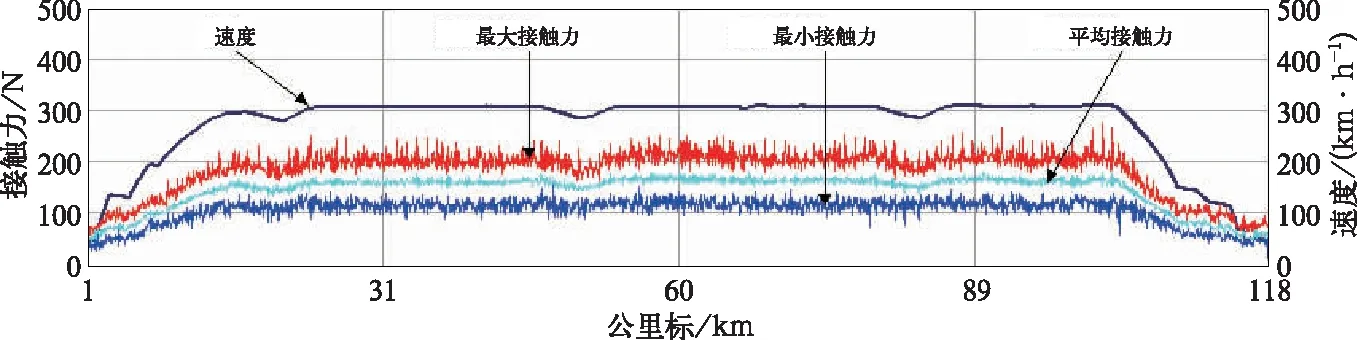
图7 下行线速度310 km/h时接触压力变化图(受电弓开口)

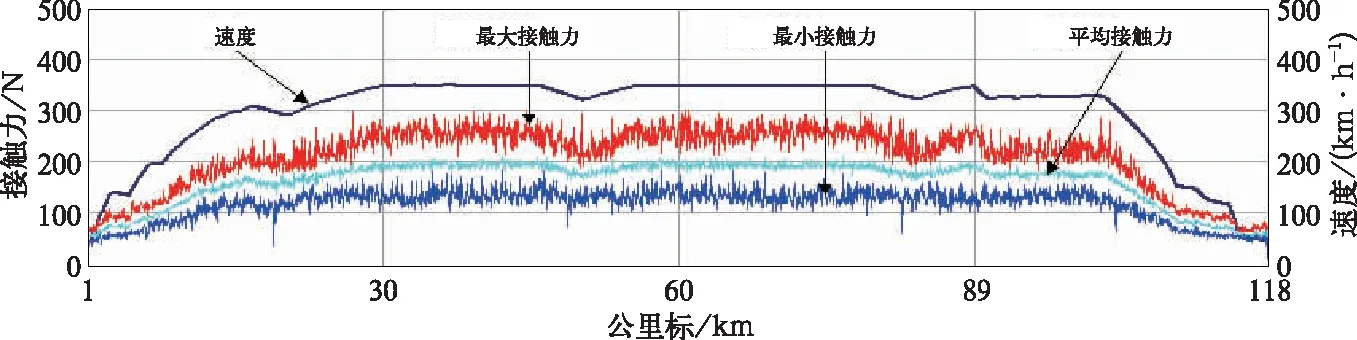
图8 下行线速度为350 km/h时接触压力变化图(受电弓开口)

图9 上行线速度为310 km/h时接触压力变化图(受电弓闭口)

图10 上行线速度为350 km/h时接触压力变化图(受电弓闭口)

表2 不同速度及上下行时受流指标对比表

速度/(km·h-1)上下行最大接触力/N平均接触力/N最小接触力/N接触力标准偏差/N310下行线开口110～22585～17065～13528上行线闭口110～24590～19075～14529350下行线开口105～27085～20070～15031上行线闭口115～31090～22570～16535

5 结束语

给出了弓网系统的模型及其运动方程式，然后利用python编程语言进行仿真建模，并通过对比实测数据，确定了模型的合理性，并得出了如下的结论。

(1)总的来说，随着列车速度的增加，弓网之间接触压力的变化幅度会越来越大。

(2)假如在速度相同、受电弓种类相同的情况下，受电弓状态为开口时，所受的最大压力、最小压力和平均压力的极大值都是会小于受电弓为闭口状态。而且随着速度从310 km/h增加到350 km/h，受电弓是开口还是闭口状态对接触压力影响越发的明显。由此我们可以大胆的推测出在其他参数条件相同的情况下，闭口下的工况要比开口下的工况恶劣。

改善弓网受流质量可以从两个方面入手。对于接触网而言，承力索张力和接触线张力大小的选择会影响接触压力，从而使受流质量下降，所以可以通过在一定的范围加大补偿张力来改进。但是补偿张力不宜施加得过大，因为过大的张力会影响承力索和接触线的使用寿命。

对于受电弓而言，可以寻找强度更高的受电弓、寻找更好的滑板材料和在适当的范围内提高受电弓的静态抬升力。在选择更先进受电弓材料的时候需要考虑这种新材料对接触线带来的影响，首先如果找的新材料的硬度高于现在受电弓滑板材料，那么它对于接触线的磨损就会加剧。在实际设计施工中，相比于更换接触线，更换受电弓的滑板是更加方便快捷的，也更经济。提高静态抬升力这一方案也同样面临这个问题，随着静态抬升力的提高，带来的磨损也会加剧，也就会减少受电弓滑板和接触网线材的寿命。