高速铁路AT供电系统谐波谐振频率研究
2019-07-27赵文胜崔召华
赵文胜,罗 杰,崔召华,黄 军
(1.沪昆铁路客运专线江西有限责任公司,南昌 330002; 2.中铁第四勘察设计院集团有限公司,武汉 430063;3.中交机电工程局,北京 100088)
随着交-直-交机车在电气化铁路中的大量应用,牵引供电系统的谐波特性发生变化,交-直型电力机车富含的3、5、7次等低次谐波含量大大降低,而高次谐波含量明显增加,且频谱变宽[1-4]。当电力机车注入的谐波与牵引网的谐振频率匹配时,将造成谐波放大、激发高次谐振,产生过电压、过电流,造成保护动作、设备损失[5-7]。
目前,国内外已有大量文献报道了牵引供电系统谐波谐振现象,采用传输放大法、频谱分析法、谐振模态分析、S域传递函数法[8-12]等多种方法,对谐振机理、谐振频率、谐波电流放大倍数等进行分析,考察机车数目、位置、功率、牵引网长度等因素的影响,并提出相应的抑制方法。上述研究可归纳为两种思路:一种采用Matlab、PSCAD等工具搭建机车-牵引网的联合仿真模型,用5端口乃至10端口的多导体传输线模拟牵引网,通过扫描电流、电压或牵引网阻抗的频谱,确定谐振是否发生及谐振频率[13-16],该种方法考虑了机车对谐振特性的影响,但分析、计算过程非常复杂,在线路设计阶段较难应用。另一种将列车视为理想电流源,构建牵引网链式网状结构,从牵引网分布参数造成谐波放大的角度考察谐振机理及其传输特性[17-19]。该方法在分析车网谐振时一般将牵引网等效为分布式参数的单线简化模型,确定牵引网谐振频率时非常方便[18],广泛应用的谐波放大公式也基于此。但该方法过于简单,对牵引网结构较为复杂的AT供电方式,即便经合并化简也存在接触网(T)、正馈线(F)、钢轨(R)至少3根导线,直接应用上述谐振频率公式、谐波放大公式必然有偏差,且现有文献也并未具体交代模型中相关参数如何获得。
为了简便、有效、直接地确定牵引网谐振频率,为工程设计和实际运营提供明确的指导,对AT单线牵引网进行合并化简和去耦,得到牵引网单位长度的等效电阻、电感和电容,采用双端口网络模拟牵引网,从而可计算出牵引网的谐振频率,并通过仿真验证了该计算方法的正确性。采用该种方法,在设计阶段就可以确定牵引网谐振频率,对于牵引网谐振的抑制具有重要的指导意义。
1 牵引网模型及参数计算
1.1 单线AT牵引网模型
图1为单线AT供电方式下的牵引网结构示意。将接触线C和承力索J合并(T),将钢轨R1、R2以及保护线P合并(R),则单线AT供电方式下的牵引网可简化为T、R、F三导体组成的系统。
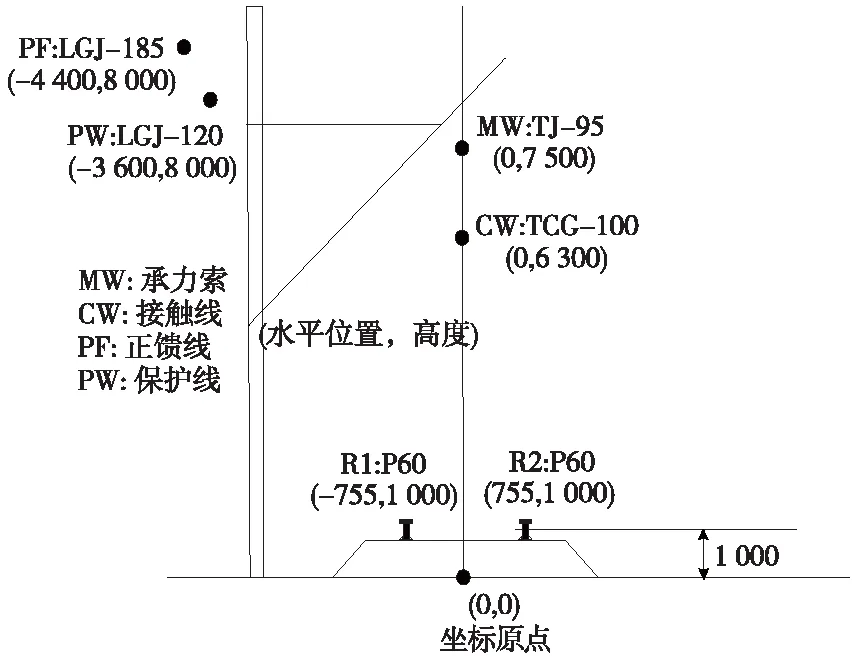
图1 单线AT牵引网结构示意
1.2 接触网阻抗计算
对于单线AT牵引网,只要得到接触网-地回路、正馈线-地回路、钢轨和保护线-地回路3个独立的回路的阻抗参数,即可得到经过降阶合并后的等效阻抗。鉴于本文主要关注点在接触网,下面以接触网-地回路为例进行去耦计算。
将经过合并后的单位长度的牵引网进行去耦,可得到如图2所示的T,R,F三个独立的对地回路。其中Z1,Z2,Z3分别为T,F,R的自阻抗,Z12,Z23,Z13分别为T和F,F和R,T和R间的互阻抗。其具体的计算式及推导过程可参考文献[20]。
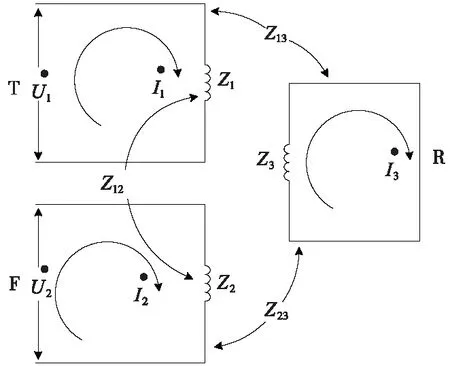
图2 T、R、F对地回路
由图2可知
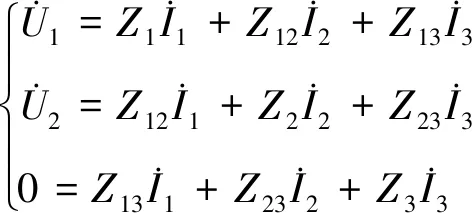
(1)
由式(1)可得
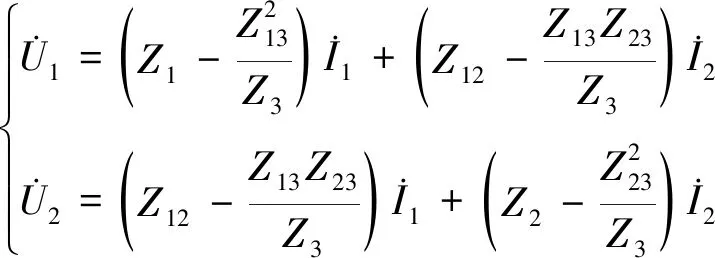
(2)
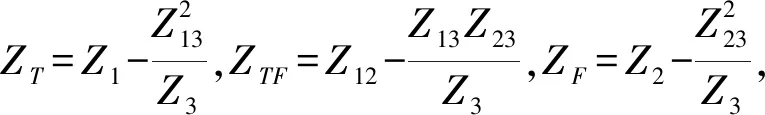
(3)
(4)
将式(4)代入式(3)可得

(5)
由式(5)可得单位长接触网对地回路等效阻抗
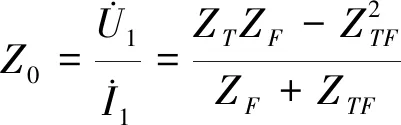
(6)
1.3 接触网电容计算
对于单线AT供电方式牵引网多导体传输线,其对地电压Ui与线电荷密度Qi之间存在下列关系
U=PQ
(7)
所以
Q=P-1U=BU
(8)
B=P-1=
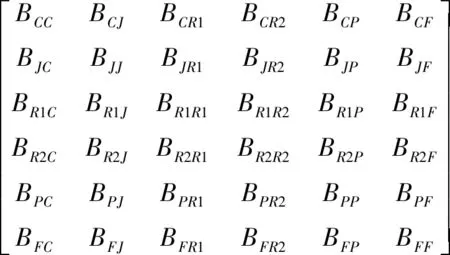
(9)
其中,P矩阵为电位系数矩阵,可通过镜像法求得,其具体计算可参考文献[17]。B矩阵为电位系数矩阵的逆矩阵,也可称为电容系数矩阵,它是电工原理中所称的静电感应系数,区别于工程上常用的支路电容即部分电容。通过P矩阵求逆即可得到B矩阵。
根据纵向连接点可对多导线进行等值合并:由于接触线和承力索每隔6~7 m用吊弦连接,并且承力索和接触线在短距离内可认为是平行传输的,所以可以将同一条线路的接触线和承力索合并成等值导线T;同时可以将同一条线路的两条钢轨和保护线合并成等值导线R。将单线AT牵引网合并为三导体后,由式(8)知
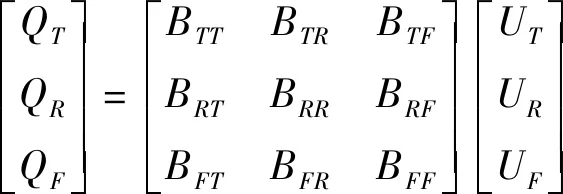
(10)
合并后的等值导线流过的电流等于需要合并的各根导线电流之和,需要合并的各根导线单位长压降相等。根据上述合并条件可得合并后的B矩阵各参数
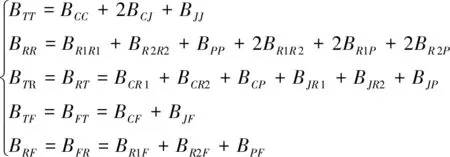
(11)
T,R,F三导体的部分电容分布如图3所示,其中CTT,CFF,CRR为导体对地的部分电容,CTF,CFR,CTR为导体之间的部分电容。
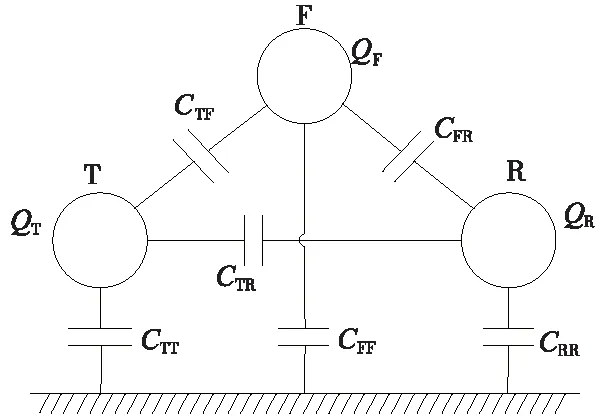
图3 三导体电容分布
设T、R、F的对地电位分别UT、UR、UF,则根据图3可知
QT=CTTUT+CTR(UT-UR)+CTF(UT-UF)=
(CTT+CTF+CTR)UT-CTRUR-CTFUF
(12)
将式(10)按矩阵乘法展开,并与式(12)比较可得
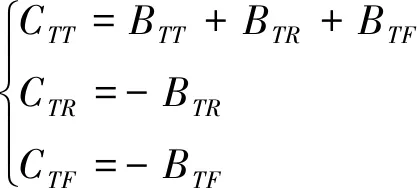
(13)
在单线AT供电系统中,UT=-UF,UR≈0,因此式(12)可改写为
QT=(CTT+CTR+2CTF)UT
(14)
所以接触网单位长度的等值电容为
C0=CTT+CTR+2CTF
(15)
2 牵引网谐振机理及谐振频率的确定
高速铁路AT供电系统主要由牵引变电所、牵引网、分区所以及机车等组成。忽略AT变漏抗以及钢轨对地过渡阻抗,可得到如图4所示的AT供电系统双端口网络等效电路。
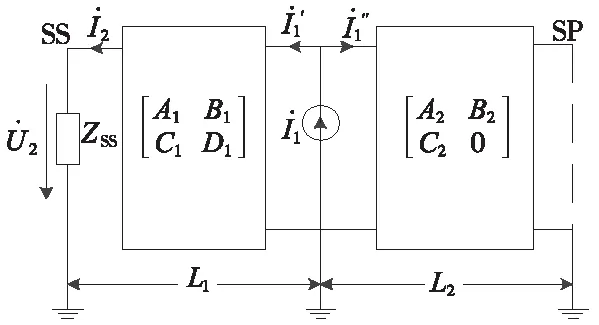
图4 AT供电系统两端口网络等效电路
其中,牵引网总长为L;Z1、Z2分别为在机车位置向牵引变电所方向和分区所方向看去的牵引网阻抗,ZSS为牵引变电所及系统的等效阻抗。
求Z1的等值双端口网络如图5所示。
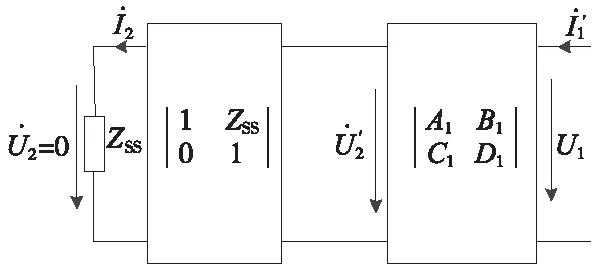
图5 求解Z1等值网络
由图5及双端口网络理论可知
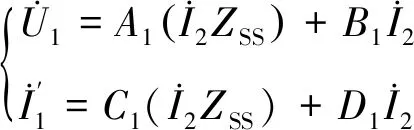
(16)
根据均匀传输线理论有
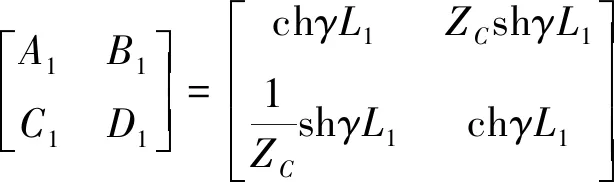
(17)
由式(16)、式(17)可得
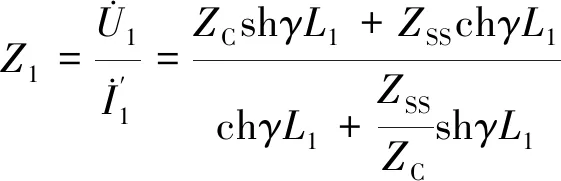
(18)
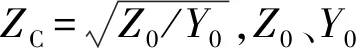
同理可得
Z2=ZCchγL2
(19)
因此,在机车处向牵引变电所方向以及向分区所方向看去,牵引网阻抗为
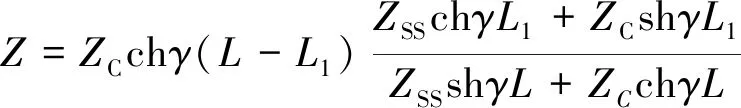
(20)
当Z=∞时牵引网发生谐振。所以谐振条件为
ZSSshγL+ZCchγL=0
(21)
设牵引变电所及系统等值电感为LSS,则由式(21)可得
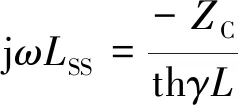
(22)
由于γL≪1,所以thγL≈γL,代入上式得
(23)
故可以得到牵引网的谐振频率为
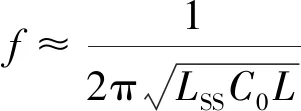
(24)
将式(15)代入式(24)可得牵引网谐振频率为
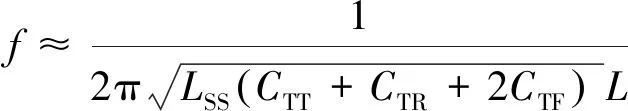
(25)
由式(25)可以看出,影响AT供电系统谐波谐振频率的主要因素有牵引网单位长度电容、牵引网长度、牵引变电所处等值阻抗等。当机车向牵引网注入的谐波频率等于或接近于牵引网的谐振点时就可能引起系统发生谐振。
3 仿真验证
本文仿真条件为:供电方式为AT单线,牵引变压器的额定容量为30 MVA,变压器变比k=110 kV/55 kV,短路电压百分数uk%=10.5%;牵引网长度L=30 km,机车选用CRH-2型动车组和理想电流源两种分别进行模拟。
3.1 车-网耦合模型的仿真
基于CRH2型动车组相关参数建立其模型,当机车位于20 km处时对牵引网的谐振特性进行仿真,结果如图6、图7所示。
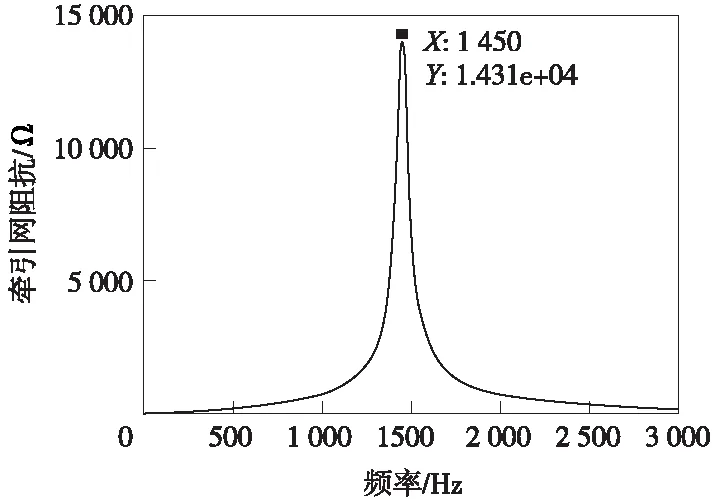
图6 牵引网阻抗频率特性曲线
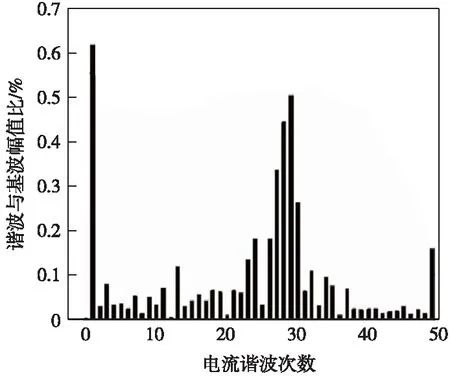
图7 网侧电压FFT分析结果
由图6可观察到,CRH动车组各次谐波在AT牵引网中传播时,在29次谐波附近阻抗出现极大值,发生并联谐振。但该谐振并未影响机车和系统运行,图7所示的网侧电压FFT分析显示其总谐畸变率低于2%国家标准,运行正常,且网侧电压中含量最大的也是29次谐波。
3.2 基于理想电流源的仿真
3.1节仿真结果显示牵引网谐振频率必然存在,但谐振并不一定产生危害。只有机车注入的谐波电流频率与牵引网谐振频率吻合,即“车网匹配”时才有可能激发严重的谐波放大[8]。
故而采用理想谐波电流源替代机车进行仿真,并在注入点将29次谐波电流值设定了一个较高的数值6.66 A,仿真得到变电所出口处的29次谐波电流为47 A,放大倍数为7.057。此时网侧电压FFT分析结果如图8所示,电压严重畸变,可以预见实际运行中发生类似状况必然导致事故,且网侧电压中含量最大的也是29次谐波。

图8 网侧电压FFT分析结果
3.3 计算所得谐振频率
牵引变电所及系统的等值阻抗为
对应的等值电感为LSS=0.033 7 H。
通过多导体传输线理论和降阶法处理后的T、F、R三导体的部分电容矩阵为

T F R
由式(15)知牵引网单位长度电容为
C0=CTT+CTR+2CTF=12.645 5 nF
故牵引网的谐振频率为
因此牵引网谐振次数为28.15次,而仿真所得到的谐振次数为29次,直接计算得到的谐振频率与仿真得到的谐振频率十分接近,说明了本文给出的谐振频率计算方法是可行的。
通过式(6)可计算出接触网单位长度阻抗Z0=0.052 3+j0.02 Ω,将参数L、L1、LSS、C0以及ZT0代入式(20)可得到如图9所示的牵引网阻抗Z随频率f变化的曲线。
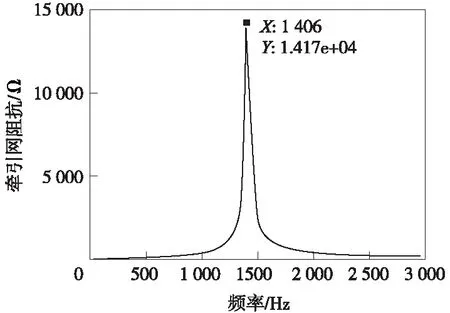
图9 阻抗随频率变化曲线
对比图6和图9可知,在机车所在位置对牵引供电系统进行阻抗频率扫描与通过参数计算所得到的牵引网阻抗随频率变化曲线基本一致。而且从图中可以观察到牵引网的谐振频率十分接近1 450 Hz(29次谐波),进一步说明了本文给出的牵引网谐振频率的计算方法是正确有效的。
4 结论
本文给出了一种计算牵引网谐振频率有效而简单的方法,得出以下结论。
(1)仿真所得的谐振频率与通过该方法计算得到的谐振频率基本一致,说明该方法是正确可靠的。
(2)通过单线AT牵引网的双端口网络等效电路获得牵引网谐振频率的表达式,对于复线以及全并联AT供电系统的牵引网谐振频率的推导具有一定的借鉴作用。
(3)对设计线路和已投运线路,可采用本文方法计算牵引网谐振频率,从而采取一定的措施抑制该次谐振频率,有效地避免或抑制牵引网谐振的发生。
