基于支持向量域描述的铁路绝缘子污秽度异常检测分析

吴文海，孙 磊，柯 坚，张 霆

(西南交通大学机械工程学院，成都 610031)

日益恶化的自然环境造成了绝缘子表面积污速度的增加，因此污闪事故发生的可能性也进一步提高[1]。KJ系列水冲洗设备，在各大铁路局使用，并取得良好的效果。然而到目前为止，由于缺乏有效的污秽度检测方法，冲洗工作的开展多数依赖于操作人员的经验，准确性差，浪费资源。为实现冲洗自动化，急需有效的绝缘子污秽度检测方法，为绝缘子清洁工作提供重要的技术前提和保障。

绝缘子的在线检测因其安装位置的特殊性及分布区域的广泛性而成为难点[2]。多年来，国内外一直在寻找有效的绝缘子在线检测方法，取得了诸多进展：泄漏电流法作为一种传统的接触式测量方法[3]具有较好的准确性，文献[4-5]把其与神经网络结合，取得了很好的效果，此种方法需为每个绝缘子安装传感器，耗材费力，难以满足实际应用需求；非接触式测量方法如红外或紫外成像技术实现绝缘子污秽状态检测[6-7]目前是国内外研究的热点，可紫外成像技术受运行电压影响较大且需在放电状态下测量，红外成像技术受环境温度影响较大，精度相对较差，影响因素较多，局限性较大；文献[8]利用可见光图像与机器学习的方法，实现了绝缘子污秽等级的分类，影响因素相对较少，可监督式学习中获取绝缘子真实污秽度相对不易，且没有考虑到真实的样本分布并处理成多分类模型。

在综合考量冲洗经验及应用需求后，提出一种采用支持向量域描述的铁路绝缘子污秽度检测方法。结果表明，该方法对解决绝缘子污秽度的异常检测问题具有良好的适应性和实用性。

1 问题的描述

等值盐密(ESDD)反映了绝缘子的污秽等级，可见光图像中反映的仅是等值灰密(NSDD)，即绝缘子上的覆灰程度。文献[8]指出：在同一地区的一段时间内，落在绝缘子表面的灰尘中的盐分的比重基本保持不变，即绝缘子表面积灰程度越严重，污秽等级也就越高。因此，可以利用图像中覆灰程度不同导致的图像特征的变化来表示等值盐密的变化，即污秽度。实际图像中能反映绝缘子污秽度的特征量很多，这些特征量与绝缘子污秽度间的相对关系多数难以直接描述，因此，想要实现图像特征与污秽度间相对关系的确定十分不易，而目前流行的机器学习正是研究这样一种从大量数据中需找描述规律的方法。

TB/T 2007-2015规定铁路绝缘子现场污秽度的测量、污秽度等级分类按照GB/T 26218.1-2010第8章进行，定义污秽度等级为很轻、轻、中等、重、很重。按照KJ系列水冲洗车的实际工作需求，简化为污染和未污染两类(即需要冲洗和不需要冲洗)，既满足了实际应用需求又减少了开发难度。室内人工涂污试验所得样本图像如图1所示，污秽样本与洁净样本的图像特征差异明显。

图1 不同污秽度绝缘子的可见光图像样本

2 图像颜色及纹理特征的计算与提取

积灰程度对于绝缘子图像三大底层特征中的形状而言影响甚小，可以忽略不记，因此针对纹理和颜色空间，通过一定的方法提取相关特征量，作为学习器的训练样本。

在提取特征之前，首先采用最大类间方差(Otsu)法对图像进行分割，去除背景对后续特征计算的干扰。Otsu法通过最大化类间方差自动选择合适的阈值，利用此阈值把图像分割为背景和目标两部分。阈值分割之后的效果如图2(b)所示，可以看出分割后的结果可以有效去除背景信息，但依然存在边缘轮廓不完整，内部含有空洞及一些细小干扰等，因此进一步地采用腐蚀、膨胀等形态学运算填补空洞，平滑轮廓边缘，去除细小干扰，最终结果见图2(c)。

图2 图像分割结果示意

对分割后的图像提取其颜色特征，颜色特征具有一定的稳定性和鲁棒性，对方向和大小不敏感，是描述图像最简单有效的特征[9]。选取图像处理中常用的4种颜色空间：RGB、HSI、Lab、YUV。颜色空间有许多表征方法如颜色直方图、颜色矩等。采用直方图来描述颜色空间，其作为一种概率统计方法，具有旋转不变性和缩放不变性等特点，在图像处理中得到广泛应用。颜色直方图通过统计方法计算出一幅图像中各颜色分量的概率p(i)，并从颜色直方图中计算出6种常用的统计量，分别为：一阶矩、二阶矩、三阶矩、四阶矩、能量、熵。

对于纹理特征提取的方法有自相关函数法，灰度共生矩阵法(GLCM)等，其中GLCM是公认的有效方法，具有很强的鲁棒性和适应能力，反映了一幅图像在方向、间隔上变化幅度及快慢的综合信息[10]。GLCM运用统计的方法计算一幅图像f(x，y)从灰度为i的像素点出发，与其距离为d，灰度为j的像素点同时出现的概率p(i，j|d，θ)，统计方向一般取0°，45°，90°，135°。并定义了对比度、能量、相关性、熵等14个统计特征值来描述纹理特征。文献[11]指出这14个特征之中存在冗余结论，其中，能量、熵、对比度和相关性间不相关，具有很好的分辨能力。

把颜色和纹理特征融合，常用的特征融合方法是将多个特征串行组合，然而其构成的多维特征向量因其自身的冗余性及高维性，造成分类器运算时间增长及识别能力下降，所以使用核主成分分析(KPCA)对特征进行提取，KPCA是一种常用的非线性降维方法，是利用核技巧对经典的主成分分析进行的非线性推广[12]，主要思想是首先通过非线性函数φ把样本数据映射到高维特征空间F，然后在F中应用PCA进行降维。假设样本X=[x1，x2，…，xN]通过φ映射到F=[φ(x1)，φ(x2)，…，φ(xN)]，映射后训练样本的协方差矩阵S为

(1)

若映射后的样本已被中心化，通过对S进行特征值分解可求得S的特征向量v和特征值λ，有

λφ(xk)v=φ(xk)Sv,k=1,2,…,N

(2)

特征向量可由特征空间F的一维坐标描述，则v可表示为

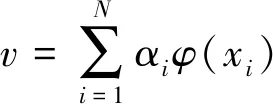
(3)

将式(1)和式(3)代入到式(2)，并引入核矩阵Kij=φ(xi)φ(xi)，即可以得到

Nλα=Kα

(4)

通过式(4)可求得特征向量和特征值，进而通过投影变换即可以确定样本在低维空间的表示。

3 基于FRSVDD的异常检测方法

由于无法穷尽样本空间的所有特征，因此传统的异常检测方法效果并不理想。而单分类的学习方法只针对正常样本进行学习形成诊断策略，对于异常检测可以取得较好的效果。其中支持向量数据描述(SVDD)以支持向量机和统计学习理论(SLT)为基础，继承了支持向量机的优点，鲁棒性好，小样本学习时具有很好的泛化能力[13]。但传统的SVDD方法侧重于对方法的探索，对数据集本身的关注程度不够，脱离实际问题背景去单纯的研究学习算法，在实际应用中效果不佳，而且SVDD以距离为度量，当输入空间的样本在各方向上距离不均匀时，最终得到的描述轮廓会包含许多空白区域，如当样本中含有离群点时SVDD易发生过拟合现象。且SVDD构造的描述边界间隔为0，泛化能力不强。文献[14]在SVDD的基础上引入粗糙集的概念，通过在特征空间寻找具有上超球和下超球结构的粗糙支持向量数据描述(RSVDD)，在一定程度上解决了这个问题，然而在RSVDD中构造超球面时，边界区域以外的数据和边界区域内的数据分别具有相同的惩罚因子C和δC，没有充分考虑样本的分布信息对超球体的影响，许多文献在传统SVDD中引入样本的分布信息，文献[15]使用KNN算法构造出密度权重SVDD，文献[16]使用局部密度改进了一种密度诱导SVDD等，都具有很好的效果。结合上述研究成果，引入一种模糊因子来描述整个数据集的分布情况，通过模糊因子对不同的样本引入不同的惩罚项，构造一个更加紧凑的模糊粗糙支持向量数据描述(FRSVDD)。FRSVDD的优化目标如式(5)所示

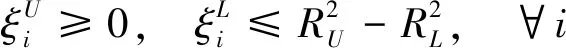
(5)

这个优化问题的解可以通过构造Lagrange函数给出，并引入核函数K(x，y)，即可把上述优化问题的对偶问题转化为二次规划问题

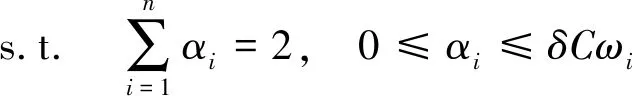
(6)

求解这个二次规划问题可以得到Lagrange乘子αi，而且超球体的球心为

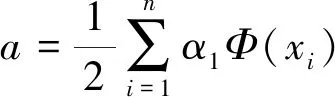
(7)

根据KKT条件，得到下述结论：

(1)αi=0对应的数据点位于下超球边界内；

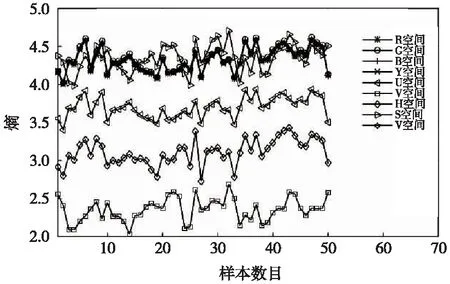
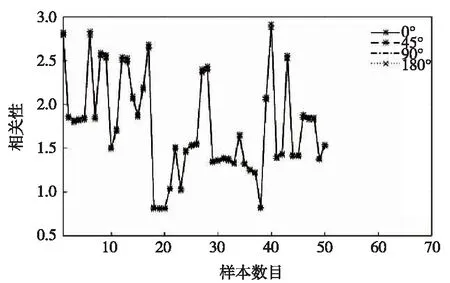
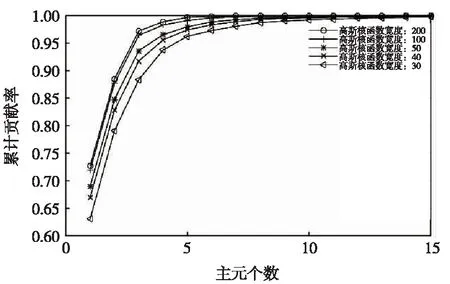
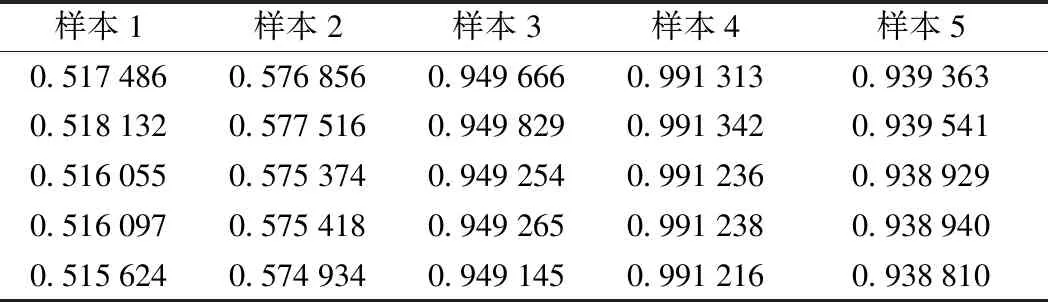
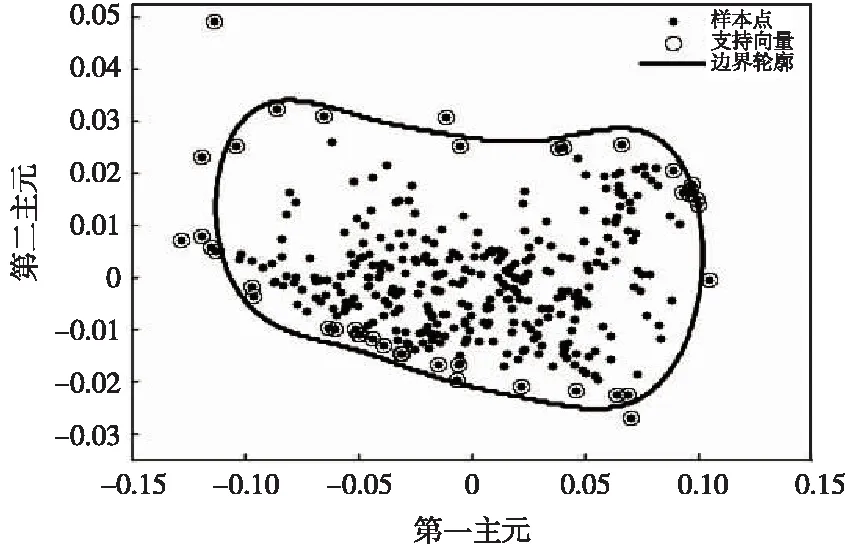
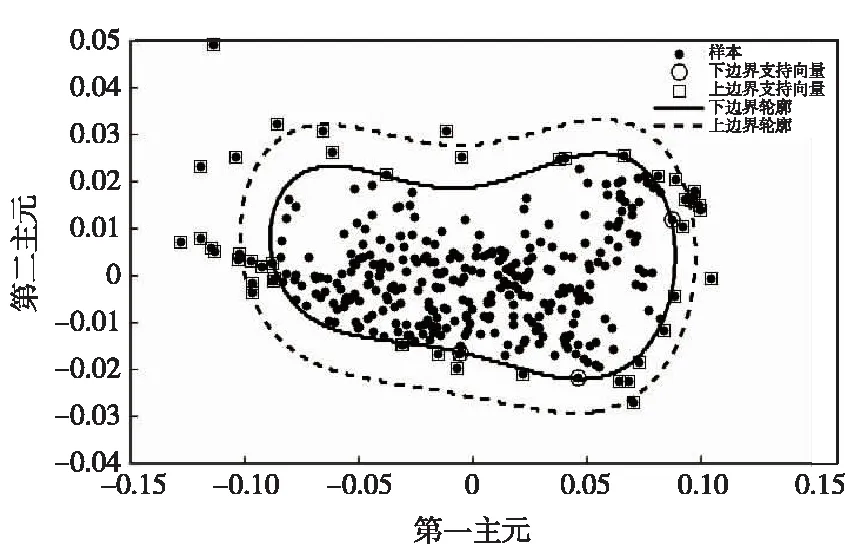
(2)0<αi

(3)αi=Cωi对应的数据点位于下超球边界外且位于上超球边界内，即可能性区域；

(4)Cωi<αi<δCωi对应的数据点位于上超球边界上；

(5)αi=δCωi对应的数据点位于上超球的边界外。

RU与RL分别为上超球半径与下超球半径，结合式(7)进而可确定上下边界轮廓。而对于任意一个测试样本点，其与超球中心a的距离与上、下超球半径作出比较即可判断测试样本污秽度的异常。

其中模糊因子ωi的确定使用可能性1-聚类算法(PCM，C=1)实现，PCM在模糊均值聚类(FCM)的基础上放宽了对隶属程度的约束，使得隶属度不再是对1的共享或者划分，聚类结果受噪声点的干扰程度较小，具有较好的鲁棒性。且P1M具有良好的全局收敛性，可以在很大程度上保证每个模糊因子是对数据描述轮廓中心的度量。

4 实验与结果分析

为验证方法的可行性，按照绝缘子污秽标准进行室内人工涂污实验并采集样本图像共806张，随机选取图像作为训练集，其余作为测试集，每次实验保证训练集数量在600以上。对分割之后的图像一方面使用颜色直方图提取出RGB、HSV、YUV空间中的均值、方差、偏差、峰度、能量、熵共54个特征值，另一方面使用GLCM提取出0°、45°、90°、135°四个方向上的能量、熵、对比度、相关性共计16个特征，其中部分特征结果列举如图3、图4所示。可以看出，大部分特征对NSDD都很敏感，可以作为样本输入到学习器中很好地进行训练，比如各颜色空间中的熵如图3所示；可有些特征值之间存在冗余结论，如图4所示，不同样本图像纹理空间相关性整体趋势相同，可用一个方向表示。

图3 不同样本图像颜色空间的熵

图4 不同样本图像纹理空间的相关性

图5 各主元的累积贡献率

使用KPCA对样本空间进行降维，其中核函数选用高斯核函数，各主元的累积贡献率如图5所示，可以看出核函数宽度对累积贡献率的影响很大，为了在保留尽可能多的主成分的情况下实现可视化的分析，综合考量之后选取核函数宽度为200，选用前二维主元在低维空间中表示原始数据，累积贡献率达到88.50%，能保留绝大部分原始空间的信息。

对降维后的二维样本，首先使用P1M进行学习训练确定模糊因子ωi，其中模糊程度系数设置为3，由于P1M随机初始化聚类中心和隶属度，并通过迭代的方法得到的模糊因子ωi，因此结果具有一定的随机性，应多次测量取平均值，实验结果表明取5次测量结果的平均值可满足应用需求，如表1所示。

表1 部分样本对样本中心隶属度的平均值(5次测量结果)

把ωi引入到SVDD和RSVDD中，确定模糊数据描述和模糊粗糙的数据描述边界，其中核函数选用高斯核函数，如图6(σ=0.05，C=0.09)和图7所示(δ=20，C=0.004，σ=0.05)。

图6 FSVDD结果示意

图7 FRSVDD结果示意

从图6可以看出，SVDD通过最小包围超球，把样本分割成两个部分，超球内的是不需要冲洗的正常样本，超球外的是需要冲洗的异常样本，鉴于样本不具备显著分离特性，所以没有一个很明确的界限来分割异常和正常区域，无法调整得到最佳参数。由图7可以看出，新增加的超球形成了上下边界轮廓，把数据分隔成3个部分：位于下边界轮廓曲线内的样本认为是正常样本，不需要冲洗；位于上边界轮廓曲线外的样本为异常样本，需要冲洗；而位于上下边界曲线内的样本可能为异常样本，可交由人工加以判别选择是否冲洗，在实际使用过程中漏警率是必须要考虑的评价指标，本着尽量减少漏警率(可能污闪的样本尽量冲洗)的原则对分布在此区域内的样本应尽量选择冲洗。因此在较少的先验知识下模糊区域可以尽可能的权衡虚警率和漏警率，以选择合适的参数。SVDD与RSVDD对比实验的部分数据见表2，其中两种方法分类得到的负样本集一致。根据数据对比发现，在默认第三类样本均能得到正确分类的前提下，RSVDD大幅降低了漏警率，并且有效降低了虚警率，可显著提高实际工作效率。

表2 SVDD与RSVDD部分实验数据对比

5 结论

由于现场污秽度测量困难且精度较低，本文提出了另一个解决方案，使用SVDD的方法实现铁路绝缘子污秽度的异常检测，为水冲洗工作的开展提供一种有效的参考和技术前提。并且引入模糊因子构造模糊RSVDD，边界轮廓更加紧凑，很好解决了SVDD鲁棒性不强及容易产生过拟合问题，并通过模糊区域有效降低虚警率和漏警率，以满足实际工作需求。