新建隧道下穿高速公路动力响应及变形控制研究
2019-07-27王志岗
董 捷,王志岗,仲 帅
(1.河北建筑工程学院土木工程学院,河北张家口 075000;2.河北省土木工程诊断、改造与抗灾重点实验室,河北张家口 075000)
引言
近年来,随着我国铁路交通事业的迅猛发展,铁路线路网密度不断增大,使得新建隧道工程不可避免地下穿既有工程构筑物。在近接下穿工程的施工过程中,考虑到既有工程构筑物荷载等不利因素的影响,有必要对新建隧道和既有构筑物典型位置处的变形规律展开研究[1-4],从而保证近接穿越工程的安全施工。因此,研究新建隧道下穿高速公路的动力响应和变形控制具有重要的现实意义。
近年来,诸多学者对新建下穿隧道受静载[5-7]、高速列车荷载[8-11]或地震荷载[12-13]变形分析做了大量研究,特别是近接交叉隧道,对其所受荷载的影响分析、变形限值和动力响应强弱均有一定研究。交叉隧道建模时多采用弹塑性结构模型,以此研究动荷载作用时新建隧道的动力特性[14-16]。晏启祥[17]选用激振力函数来模拟列车经过时产生的竖向动荷载大小。通过对比发现,已有研究成果多基于下穿普通铁路或高速铁路工程,重型汽车与普通列车、高速列车相比,在载重和速度方面存在较大差异,使得上述经验规律和研究成果不能直接应用于重型汽车荷载作用时新建隧道结构动力响应特性的研究。
针对我国现有大量铁路和公路交叉工程研究成果分析可得,两者围岩夹层为30 m时正处于2.0D~3.5D(D为隧道外径)洞跨范围内的弱影响区[18-19],本文依托的新建祁家庄隧道埋深为33 m,隧道外径为14.5 m,洞跨比为2.3D处于弱影响区,因此需考虑重型汽车振动荷载对隧道拱顶沉降的影响,以确定在设计和施工阶段是否需要对交叉段内拱顶等薄弱环节做特殊考虑。鉴于以上分析,采用FLAC3D建立了基于现场振动实测的激励输入模型,对既有高速公路路基体、围岩夹层和下部隧道结构动力特性及变形规律进行分析,以期为类似近接穿越工程的安全施工提供借鉴。
1 工程概况
依托新建祁家庄双线单洞隧道近接下穿既有G6高速公路工程,祁家庄隧道位于张家口市下花园区孟家坟村北侧,该新建隧道全长5740 m,洞跨为13 m。新建隧道在设计里程DK144+694~DK144+804段下穿既有G6高速公路,其中高速公路路基体宽26 m,交叉区域新建隧道埋深33 m,如图1所示。根据超前地质预报探测结果可知隧道围岩以弱风化的凝灰质砂岩为主。

图1 近接下穿工程平面示意
上部G6高速公路是我国华北地区重要的高速公路干线,承担着大量的货运运输任务。据统计,G6高速公路某区段日通行量达16 300辆,其中重型汽车6 500辆。在长期运行条件下,重型汽车产生的振动荷载和新建下穿隧道开挖造成地层损失加剧了路基体疲劳损伤程度。为此,考虑重型汽车振动荷载的频繁作用,重点研究下部新建隧道掌子面推进至不同深度时,路基体、围岩夹层和下部隧道结构的动力特性和变形规律,以确保下穿隧道的安全施工和既有高速公路的正常运营。
2 模型的建立
2.1 基本假定
模型以新建隧道与既有高速公路交叉点为中心,沿长度、宽度和高度方向分别设为100,100 m和70 m,如图2所示。新建隧道初期支护和二次衬砌厚度分别设为250 m m和500 mm。模型建立时围岩和路基体采用Mohr-Coulomb理想弹塑性模型,支护结构均采用弹性单元,下穿隧道的初期支护采用壳单元,二次衬砌采用实体单元。
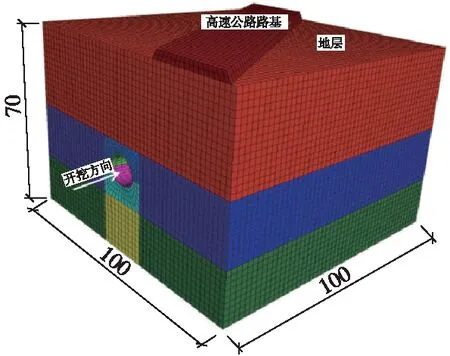
图2 三维数值计算模型(单位:m)
在静力分析阶段,模型四周边界约束法向位移,模型底部设为固定约束,上表面为自由面;动力分析过程中,模型底部和四周设置静态边界,静态边界的实现是通过在模型边界位置沿法向和切向分别设置阻尼器可有效吸收入射波[20],提高数值分析的准确性。
2.2 模型参数
根据该新建隧道现场勘察资料,并结合TB10003—2005《铁路隧道设计规范》,模型材料计算参数取值见表1[21]。
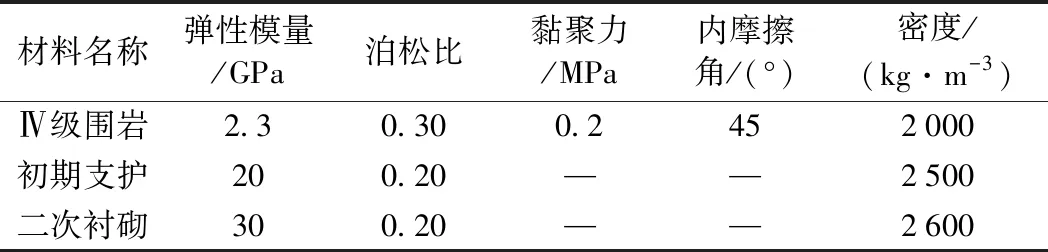
表1 围岩和支护结构计算参数
3 重型汽车运动微分方程的建立
结合JTG D60—2015《公路桥涵设计通用规范》确定重型汽车的几何参数和荷载参数。基于经典力学理论,将汽车运动简化为单轨迹双质心的二维平面运动,推导出适用于重型汽车的运动微分方程,为建立基于现场振动实测的激励输入模型提供理论基础。为便于研究重型汽车的运动方程,对其做出以下简化:
(1)忽略转向系统的影响,直接以前后车轮作为荷载输入点;
(2)重型汽车前进速度视为不变;
(3)忽略汽车悬挂系统的作用,且车身做平行于路面的平面运动。
鉴于以上假设,重型汽车视为单轨迹双质心模型。二自由度汽车运动方程建立如下:
考虑到汽车始终做匀速直线运动,则二自由度汽车只在平面上做匀速直线运动,运动方程为
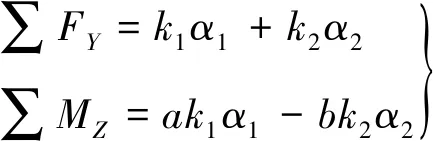
(1)
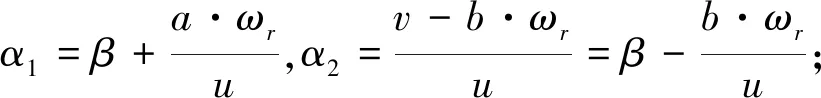
二自由度重型汽车运动微分方程为
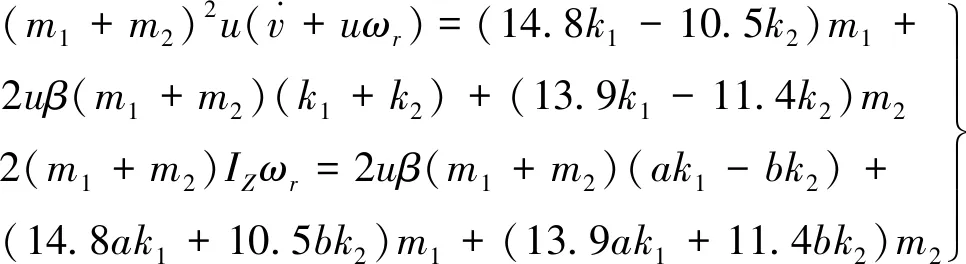
(2)
微分方程变形为
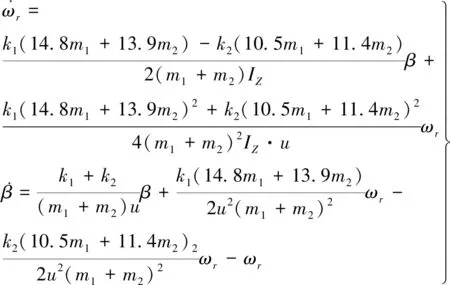
(3)
换算为二自由度重型汽车运动状态方程
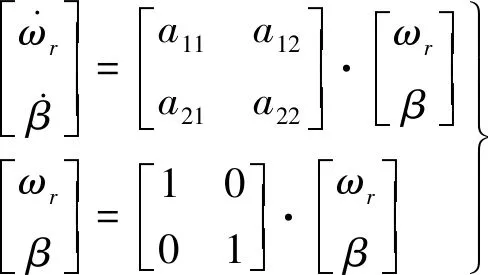
(4)
式中
4 重型汽车振动荷载的采集分析
现场加速度采集系统选用cDAQ-9174四槽盒 CompactDAQ机箱,加速度传感器使用具有高灵敏度CT1100LC型传感器[22]。结合重型汽车车辆参数,在G6高速公路某区间段选取v=70 km/h匀速行驶的重型汽车振动荷载进行采集。为降低采集过程中外界因素的干扰,使用固态胶和钢垫片将加速度传感器固定在采集区域的路面上。
现场采集系统记录了重型汽车行驶过程中振动加速度情况,实测加速度时程曲线如图3所示。
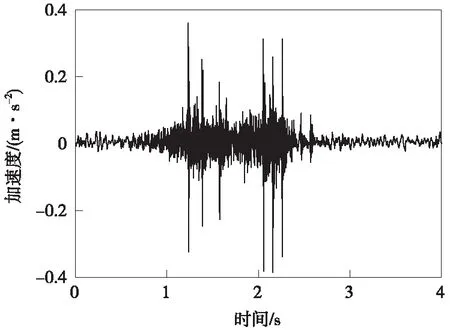
图3 重型汽车加速度时程曲线
基于重型汽车运动微分方程可知,数值模拟时实测振动荷载以线荷载的方式施加在上部隧道公路中线相邻节点处,前后相邻节点通过设置相位差来模拟车辆行驶过程中的滚动效应。考虑车辆是匀速通过相邻加载节点,使得重型汽车振动荷载在相邻节点处具有相同的相位差t0,其中
t0=l/v
(5)
式中,l为沿汽车行驶方向上相邻节点的距离;v为重型汽车实测速度。假设某节点荷载函数为Pi(t)=F(t),则下一节点的荷载函数Pi+1(t)=F(t+t0)。据此近似模拟因重型汽车行驶对路基产生振动激励的整个过程。
5 计算结果
该近接交叉工程以沿公路两侧线路中线施加重型汽车振动荷载为最不利状态开展研究。根据模型尺寸和振动传播规律,选取沿行驶方向交叉点前后各40 m范围作为研究区域,重型汽车从公路两段以70 km/h的速度相向行驶,列车从进入研究区域到驶离的时间为4 s。选取y=50 m横断面(即交叉横断面)为目标断面[23],在目标断面内高速公路路基体单元、围岩夹层(路基表层与隧道拱顶之间每个监测点在竖直方向均间隔6 m)和隧道典型位置处布设监测点,进行动力响应和变形规律研究,如图4所示。
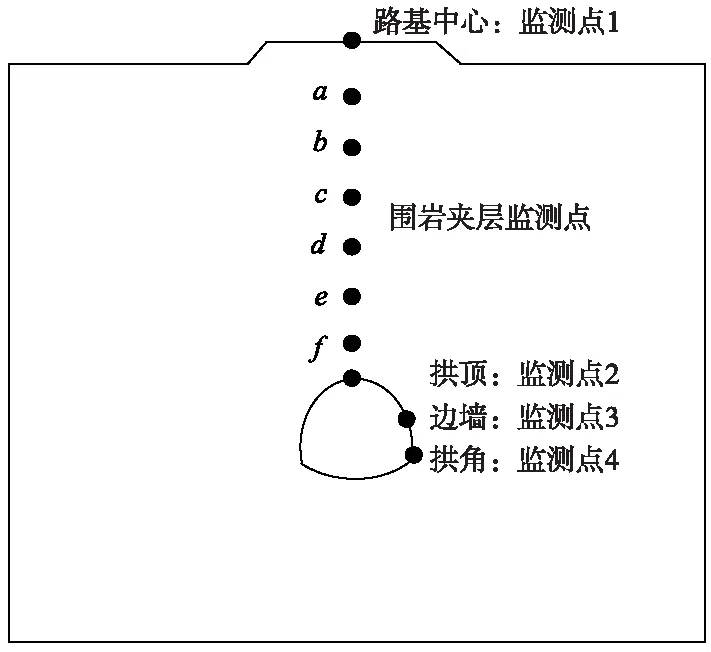
图4 目标断面监测点布置
下部新建隧道采用上下台阶法施工,循环进尺取为2 m。根据建技[2010]352号及铁建设[2010]120 号文规定,确定下部新建隧道初期支护和二次衬砌的安全步距为25 m和50 m。选取隧道开挖深度为50,52,76 m和100 m进行分析,研究施加重型汽车振动荷载时各监测点的动力学行为。
5.1 路基表面监测点的动位移分析
随着重型汽车振动荷载的移动,分析对比不同开挖深度时,高速公路路基体监测点的竖向位移时程曲线,如图5所示。
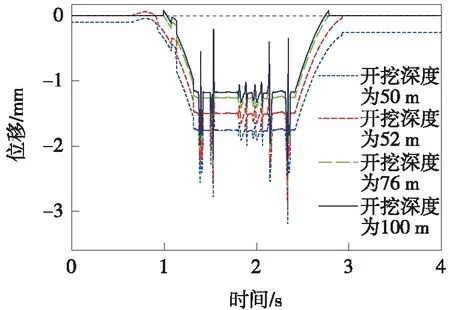
图5 路基表层监测点竖向位移时程曲线
重型汽车荷载移动过程中,隧道开挖深度的不同对于高速公路路基体表层峰值位移的影响,如表2所示。

表2 路基表层监测点峰值位移 mm
通过比较路基表层监测点竖向位移时程曲线和峰值位移可得出如下结论。
(1)重型汽车依次经过目标断面时,路基表层监测点的位移时程曲线呈现出周期性变化,表明监测点土体单元在汽车经过时受到循环荷载的作用。在重型汽车振动荷载的激励作用下,路基表层监测点的位移时程曲线和现场实测加速度时程曲线的变化趋势具有较好的一致性。
(2)重型汽车在驶入和驶离监测断面的过程中,监测点位移时程曲线有明显的加载和卸载过程。受到重型汽车荷载叠加效应的影响,路基表层监测点的动位移在2.38 s时达到最大值,为3.19 mm;当重型汽车荷载驶离目标断面后,动位移曲线变化逐渐趋于平缓。
(3)隧道初期支护施作完成后,路基表层监测点竖向位移峰值为2.62 mm,较开挖深度50 m和52 m分别减小了0.31 mm和0.57 mm;隧道二次衬砌封闭成环时,路基表层监测点位移峰值为2.44 mm,较开挖深度为50,52 m和76 m分别减小了23.5%,16.87%和6.87%,表明及时施作初期支护和二次衬砌可有效减小路基面沉降。
5.2 围岩夹层的动应力分析
为研究施加重型汽车激励荷载作用下不同深度围岩的动力响应,对围岩夹层内各监测点(监测点a~f)的动应力进行监测,动应力时程曲线结果如图6所示。
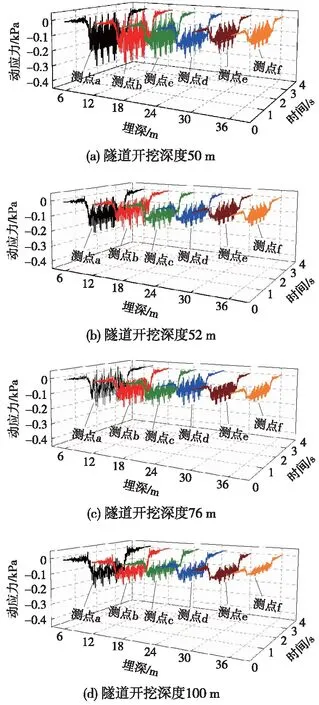
图6 围岩夹层监测点应力时程曲线
围岩夹层内监测点的动应力峰值,如表3所示。
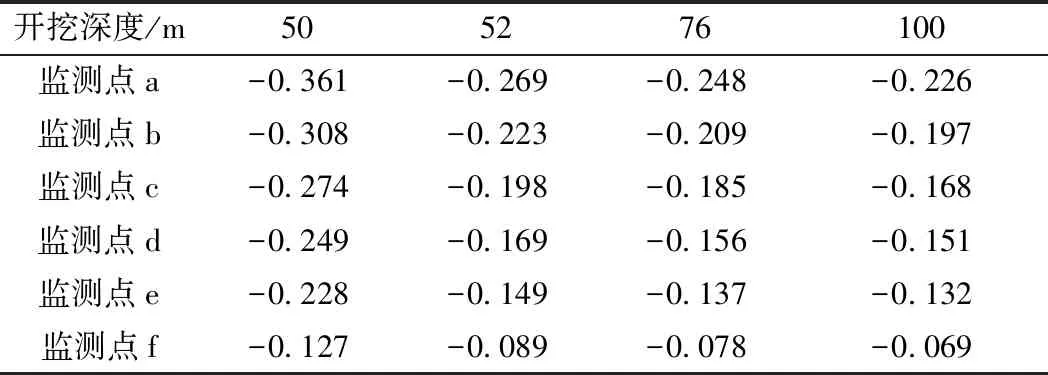
表3 围岩夹层内监测点动应力峰值 kPa
结合围岩夹层监测点动应力时程曲线和动应力峰值分析可得如下结论。
(1)根据围岩夹层监测点应力时程曲线可知,围岩夹层监测点起振点的时间随测点深度的增加而延迟,呈现出一定的滞后性。
(2)围岩夹层动应力随掌子面的向前推进而逐渐减小。隧道开挖深度为50 m时,监测点a最大动应力为0.361 kPa,当开挖深度为52,76 m和100 m,最大动应力分别减小了25.49%,31.31%和37.40%。这是由于交叉区域内隧道开挖完成后使得临空面不断增大,围岩体产生了一定量的沉降,导致围岩夹层应力在一定程度上得到释放。
(3)隧道开挖导致部分围岩体进入塑性状态,形成应力-应变滞回圈导致一定范围内的动应力大量消散,致使隧道拱顶位置处应力锐减。以开挖深度50 m为例分析,测点b~测点f较测点a的动应力峰值分别减小了0.053,0.087,0.112,0.132 kPa和0.233 kPa。
5.3 隧道拱顶动位移特征分析
随着掌子面的不断推进,在重型汽车振动荷载作用下监测下部隧道拱顶的动位移,如图7所示。
通过对比不同开挖深度时拱顶监测点的位移时程曲线可以得出如下结论。
(1)下部隧道掌子面推进至目标断面时,隧道的初始下沉值仅为0.193 mm,而当掌子面已经通过目标断面开挖至52 m时,此时拱顶位移峰值增加到0.226 mm,比前者增大了17.1%,表明隧道拱顶大变形区域出现在掌子面后方,在施工过程中应注意防范,避免拱顶出现整体下沉从而导致大面积塌腔的出现。
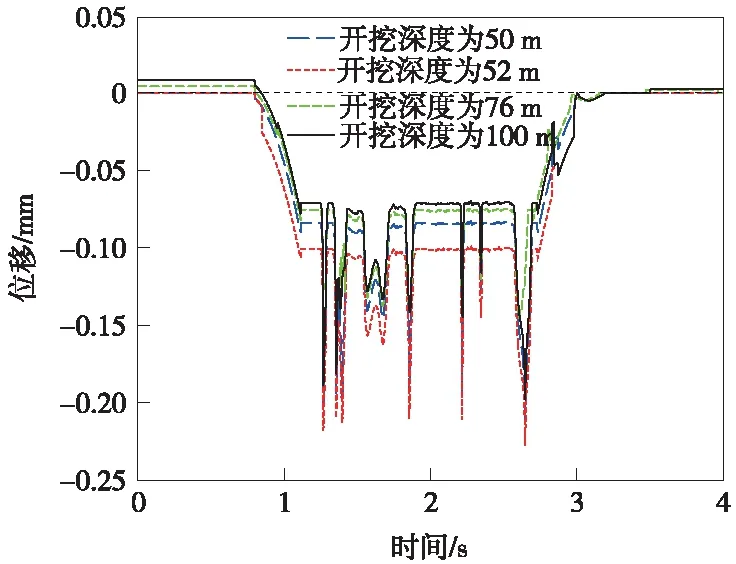
图7 隧道拱顶竖向位移时程曲线
(2)掌子面推进至76 m位置处时,初期支护施作到目标断面,隧道拱顶沉降位移峰值为0.171 mm,比尚未支护时隧道拱顶位移分别减小了0.022 mm和0.055 mm,初期支护可有效的抑制局部围岩体塑性变形的发展,同时抑制了变形引起的围岩松弛。
(3)当隧道二次衬砌闭合成环(即隧道开挖完成),对比开挖深度为50,52 m和76 m,隧道拱顶峰值位移分别减小了17.6%,29.6%和7.1%,在安全步距内施作二次衬砌可避免围岩流变性卸载等不利现象的发生,有效减小了最终位移值,从而降低了围岩坍塌导致隧道关门灾害发生的几率。
5.4 隧道典型监测点的动应力特征分析
新建隧道拱顶、边墙和拱脚监测点处竖向应力时程曲线如图8所示。
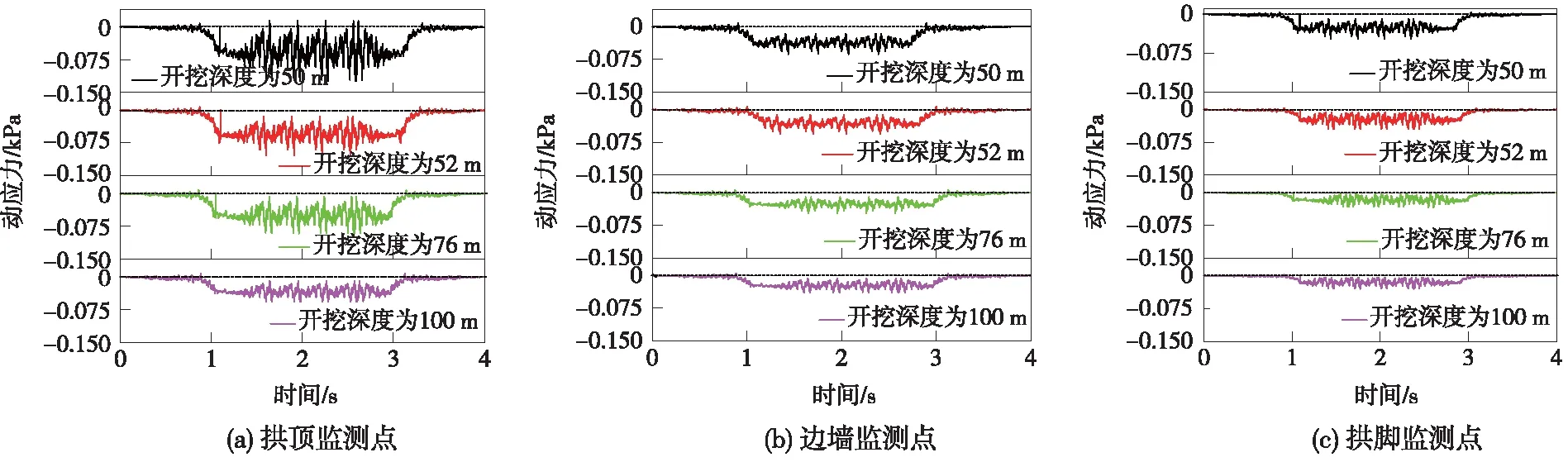
图8 下部隧道监测点应力时程曲线
当隧道开挖至不同深度时,各监测点的最大动应力峰值如表4所示。

表4 隧道典型监测点动应力峰值 kPa
根据隧道拱顶、边墙和拱脚监测点应力时程曲线和动应力峰值可得出如下结论。
(1)隧道典型监测点的动应力时程曲线大体相同,呈整体运动趋势,掌子面的向前推进不影响其动应力时程曲线的趋势。
(2)随着隧道埋深的增加,围岩体对结构的约束增强,使得新建隧道自拱顶至拱脚的动应力响应就越弱。以开挖深度为50 m为例分析,边墙和拱脚的应力峰值分别为0.068,0.048 kPa,与拱顶动应力峰值相比,动力峰值分别减小了39.82%和57.52%。
(3)下部隧道围岩应力曲线有明显的突变点。随着掌子面不断向前推进,拱顶峰值应力递减,较初始应力值分别减小了0.008,0.032 kPa和0.048 kPa。隧道实际施工生产过程中,及时施加初期支护和二次衬砌,可避免衬砌结构承受超预期的变形压力,有效的防止衬砌结构产生大变形。
6 结论
依托新建隧道下穿既有高速公路工程,建立基于现场振动实测激励输入模型,对比分析重型汽车荷载作用下路基体、围岩夹层和隧道结构的动力学行为,主要结论如下。
(1)在重型汽车进入和驶离目标断面时,路基监测点动位移时程曲线呈现出周期性。由于汽车荷载叠加效应的存在,使得路基动应力影响范围大幅增加,表现为2.38 s时路基监测点竖向位移达到最大值为2.93 mm。
(2)动应力自上而下逐渐衰减,测点a至隧道拱顶动应力衰减幅值达0.248 kPa,较初始状态动应力累积衰减68.7%。围岩夹层动应力自上而下衰减速率逐渐降低,但在隧道洞周围岩塑性区一定范围内由于振动波出现急剧的能量损失,造成动应力衰减速率突然增加。
(3)对比发现,重型汽车运行引起的拱顶峰值下沉量相比隧道开挖引起的变形量较大,拱顶动位移峰值达0.226 mm;当下部隧道以循环进尺为2 m的上下台阶法开挖时,新建隧道拱顶沉降较小,仅为0.14 mm,均满足对隧道沉降变形的控制要求[22]。表明基于规范设计的祁家庄隧道衬砌结构是较安全的,在合理要求的基础上留有充足的安全储备。
(4)分析表明,本穿越工程采用循环进尺为2 m的上下台阶法施工是相对合理的,可保证下部隧道安全通过危险区域。当前祁家庄隧道已全线贯通,采用本文的研究成果有效地指导了该复杂穿越工程的施工,研究成果对类似工程建设具有一定的指导意义。
