双线地铁盾构施工引起的地表沉降分析及施工控制

2019-07-27鞠鑫

铁道标准设计 2019年8期

鞠鑫

(1.兰州理工大学甘肃土木工程防灾减灾重点实验室，兰州 730050；2.兰州理工大学西部土木工程防灾减灾教育部工程研究中心，兰州 730050)

随着我国城市现代化的高速发展，地面交通已经不能满足人们日益增长的出行需求，因此，很多城市将交通系统的开发利用转向地下。盾构法以其速度快、精度高、不影响地面交通等诸多优点，成为软土地层地铁隧道开挖的主要方法[1]，而盾构施工不可避免地会对周围岩土体产生扰动，诱发隧道上方地表沉降。地表沉降会对地面交通、地下管线和既有建筑物产生不利影响，引发一系列工程问题。因此，针对软土地区盾构隧道施工引起的地表沉降进行研究具有十分重要的应用价值。

目前，针对双线地铁盾构开挖引起的地表沉降问题，国内外学者已经开展了大量的研究，并提出了地表沉降的经验计算方法[2]，如：Peck公式[3]、修正的Peck公式[4]、Sagaseta公式[5]等，这些公式可以在一定程度上反映地表沉降规律。在理论研究方面，方恩权[6]利用插值法和最小二乘法对Peck公式进行修正，提出了适用于盾构隧道的地层沉降预测公式；沈培良[7]提出了地铁盾构隧道纵、横断面上地表沉降分布的修正公式，并验证了其适用性；丁智[8]考虑盾构掘进引起的土体损失率，给出了修正的Sagaseta公式，并基于盾构掘进区协同作用力学模型，研究了建筑物刚度、地基基床系数等因素对建筑物变形的影响。试验研究方面，范祚文[9]利用土压平衡盾构模型试验，分析了砂卵石地层中盾构施工引起的地层沉降规律；张杰[10]通过模型试验研究了软弱富水地层浅埋隧道的地表沉降规律。现场监测分析方面，路林海[11]基于Peck公式，结合实测数据，提出了曲线盾构施工地表沉降预测公式；韩煊[12]基于实测资料，考虑建筑物结构的刚度，提出了建筑物沉降曲线的预测方法。此外，有限单元法[13-14]、随机介质理论[15]和神经网络方法[16]也广泛应用于浅埋隧道开挖引起的地表沉降问题，并取得了显著的效果，但地下工程的施工是个复杂的过程，盾构隧道所处地层、埋深、间距、左右线施工的先后顺序等均不同，因此，选择合适的地表沉降计算方法尤为重要。

在盾构隧道地表沉降施工控制方面，主要包括同步注浆改进[17]、土舱压力优化[18]、推进速度控制[19]、管片拼装控制[20]及刀盘和螺旋机扭矩控制[17]。但上述控制措施的提出都是基于现场试验的，而现场试验往往具有一定的局限性。

综上所述，现有的研究工作主要集中在现场沉降监测分析[21-22]和单线隧道施工引起的地表沉降分析[3，6，23]，对于双线隧道盾构施工引起的地表沉降计算，仍然处于半经验半理论阶段。考虑到地下工程的复杂性、特殊性及施工技术差异，本文首先总结了双线隧道地表沉降计算方法，讨论了双孔平行隧道地表沉降计算公式在厦门地铁某区间隧道中的适用性，在分析该区间隧道地表沉降规律及动态变形过程的基础上，提出了软土盾构隧道地表沉降控制技术措施。

1 地表沉降预测方法

1.1 基于统计理论的Peck公式

Peck[3]基于大量的实测资料，提出了地表沉降槽近似于正态分布的理论和地层损失的概念，其预测方法表达式为

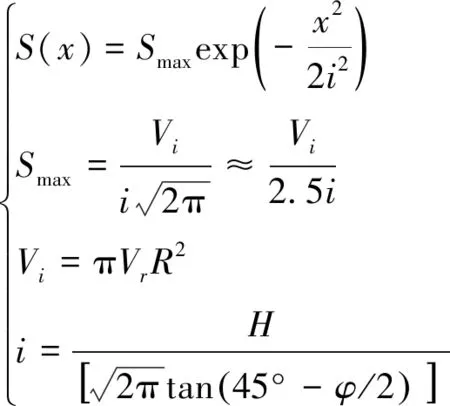
(1)

式中，S(x)为距离隧道中心轴线x处的地表沉降值；Smax为隧道中心线处的地表最大沉降值；i为地表沉降槽宽度系数，即隧道中心点至沉降曲线反弯点的距离；Vi为开挖引起的隧道单位长度的地层损失，即为隧道施工实际开挖的土体和隧道竣工之后的体积差；Vr为地层体积损失率；R为隧道计算半径；H为隧道埋深；φ为土体内摩擦角。

Peck经验公式是在大量实测数据的基础上通过统计分析所得，适用于均匀地层条件下浅埋隧道对称沉降槽分析，但实际工程中多为双线平行隧道，且左、右线距离较近，两隧道在施工中会产生相互影响，导致双线隧道地表沉降曲线分布不同于单线隧道。

1.2 修正Sagaseta公式

魏纲等[25]参考Sagaseta C[5，26]和Loganathan N[27]所提出的地层位移预测解析解，考虑泊松比以及土体变形，采用椭圆形非等量径向位移模式的修正Sagaseta公式为

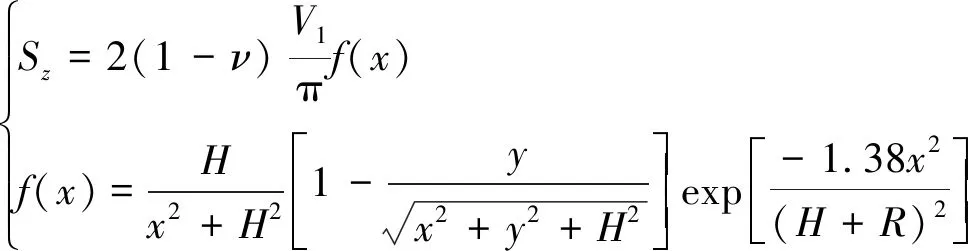
(2)

式中，Sz为距离隧道中心轴线x处的地表沉降值；ν为泊松比；x为距离两隧道中心轴线水平距离；y为距离开挖面的水平距离；V1为单位长度的地层损失量；H为隧道埋深；其他参数含义同上。

而事实上，当双线盾构隧道左、右线隧道间距较小时，相互扰动作用较显著，即表现为“V”形沉降槽[28]；左、右线隧道距离较大时，相互扰动作用较弱，即表现为“W”形沉降槽。此外，地表沉降还受施工先后顺序、隧道间距、埋深、土层参数等的影响，出现非对称的情况。

1.3 双孔平行隧道地表沉降计算公式

基于上述分析，邱明明[28]结合弹性理论，在修正Sagaseta公式的基础上，给出了双孔平行隧道地表沉降预测公式

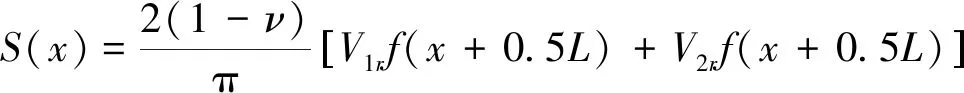
(3)

式中，S(x)为距离隧道中心轴线x处的地表沉降值；L为两隧道之间中心间距；V1r、V2r分别为先行隧道和后行隧道开挖单位长度的地层损失量；其他参数含义同上。双孔平行隧道地表沉降计算公式的建立考虑了隧道间距、埋深、土体内摩擦角及施工条件的影响，可以较好地反映双线隧道地表沉降的“W”形特征的非对称性，并在工程实例中验证了其适用性[28]。

2 地表沉降变形特性分析

2.1 工程概况

厦门市地铁2号线某区间盾构隧道全长约为2 750 m，地势较平坦，南高北低，地面高差为1.4～3.2 m。区间隧道主要穿越城市道路、居民区空地、绿化带及低层住宅楼，平面线间距为11.5～13.8 m，埋深13.2～16.7 m。管片采用双面楔形通用环，内径5.5 m，幅宽为1.2 m，楔形量为40 mm，每环管片由6块组成，采用错缝拼装，联络通道处采用特殊管片，通缝拼装。

本文所涉及的研究区段，场区内不良地质现象与地表水不发育，地下水主要为第四系孔隙水和基岩裂隙水，第四系孔隙水主要赋存于冲洪积、海积砂层中，以孔隙潜水位为主，人工填土层中局部存在上层滞水，基岩裂隙水主要赋存于基岩强、中风化带中，地下水位埋深为15.5～18.2 m。根据钻孔揭露，地层自上而下依次划分为杂填土(0～0.5 m)、素填土(0.5～2.3 m)、粉质黏土(2.3～8.5 m)、残积砂质黏土(8.5～18 m)、全风化花岗岩(18～24.1 m)。隧道采用泥水平衡盾构法施工，初始同步注浆量为2.4 m3、土舱压力值为0.12 MPa，开挖主要在残积砂质黏土中进行，残积砂质黏土颗粒呈“两头大，中间小”的特征分布，这种独特的组分特征，使其既具有砂土的特征，亦具有黏土的特性，同时也为小颗粒从大颗粒的孔隙中涌出提供可能的条件，因此，该层在动水压力作用下，易产生管涌、流土等渗透变形现象。

2.2 监测点布置

为了分析盾构开挖引起的地表沉降规律及动态变形过程，选取该段车辆和行人荷载影响较小的区域，布置S1和S2两个监测断面，共38个横向测点，对双线隧道地表沉降值进行实测。S1断面距地铁车站30 m，两个监测断面之间间距为10 m，测点间的横向距离为4 m。现场监测点具体布置如图1所示。

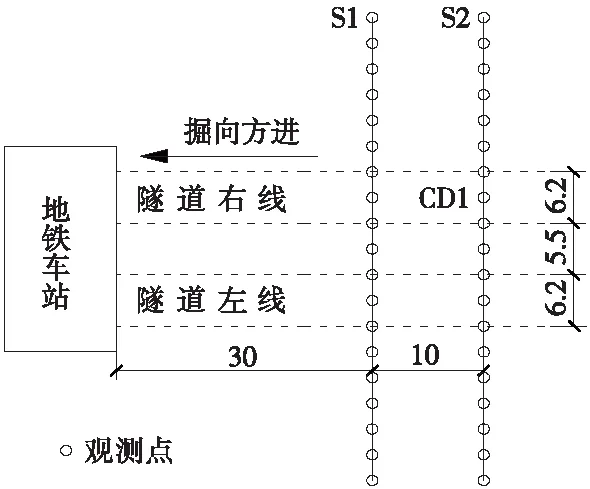
图1 地表沉降监测断面布置示意(单位:m)

2.3 模型建立

采用ABAQUS有限元分析软件，为了减小边界效应的影响，考虑隧道开挖对土体的扰动及其影响范围为3～5倍的洞径，三维有限元数值模型如图2所示，尺寸为100 m×60 m×80 m，隧道外径为6.2 m，隧道埋深15 m，两隧道轴线间距11.7 m，管片厚度0.35 m，幅宽1.2 m。

根据勘察单位提供的参数分析报告，土体计算采用Mohr-Coulomb弹塑性模型，衬砌管片采用弹性模型，对土层参数加权平均后，应用于数值模型中，具体计算参数见表1。模型左、右和前、后边界均施加法向约束，底部边界完全固定。设置土体侧压力系数为0.6，假定盾构开挖引起的土体损失沿管片周围均匀分布，根据文献[29]的研究成果，土体损失率取3%。在模型中预先设定土体、管片、等效注浆层，在模拟盾构开挖时，通过改变单元材料类型的方法来实现。

2.4 地表最终沉降预测与对比分析

基于三维有限元模拟方法，对本文所涉及的区间盾构施工引起的地表沉降进行计算，将计算结果与现场实测最终沉降值和双孔平行隧道地表沉降计算公式计算结果进行对比。图3为隧道施工完成后，S1断面和S2断面的地面最终沉降拟合曲线，三者拟合曲线趋势基本吻合，各方法所得地表沉降曲线都能反映沉降槽的“W”形特性，双孔平行隧道地表沉降计算公式考虑左、右线开挖顺序，计算值较好地反映了“W”形沉降槽的非对称性。因此，双孔平行隧道地表沉降预测公式提供的地表沉降计算方法适用于本项目。

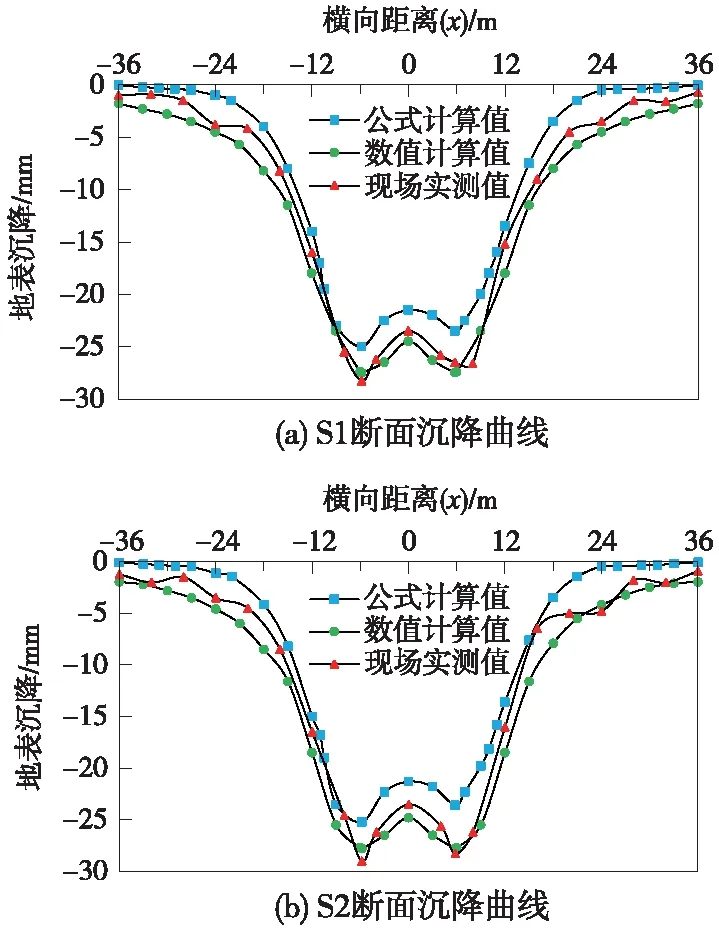
图3 双线盾构开挖引起的地表沉降曲线比较

由图3可以看出，左、右线隧道施工完成后，S1断面和S2断面处，数值模拟所得地表沉降槽是对称分布的，但双孔平行隧道地表沉降计算公式计算值和实测数据呈现的地表沉降槽不具对称性，这是由于数值模拟中没有考虑盾构机的偏斜和左、右线开挖先后顺序。

由双孔平行隧道地表沉降计算公式计算、现场实测及数值计算所得地表最终沉降值如表2所示。从图3和表2可以看出，双线隧道施工完成后，地表沉降影响范围较大，沉降槽宽度约为70～80 m。与实测值和数值计算值相比，双孔平行隧道地表沉降计算公式计算所得地表沉降值偏小2～5 mm，同时计算得到的地面沉降槽宽度也偏小。由于先行的左线隧道施工引起的地层损失较大，地表沉降最大值出现在先行施工的左线隧道。

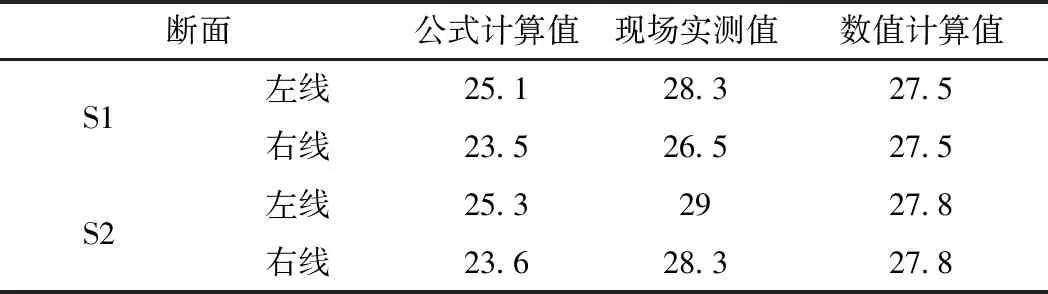
表2 最终地表沉降值 mm

2.5 地表动态变形特性

盾构开挖引起的地表沉降本质上是盾构施工引起的土体损失累积造成的，为了研究盾构施工过程中地表沉降的动态过程，选取计算模型中后行的右线隧道处S2断面作为目标面，绘制S2断面CD1测点(图1)处地表沉降与开挖面推进过程中的动态关系曲线如图4所示。

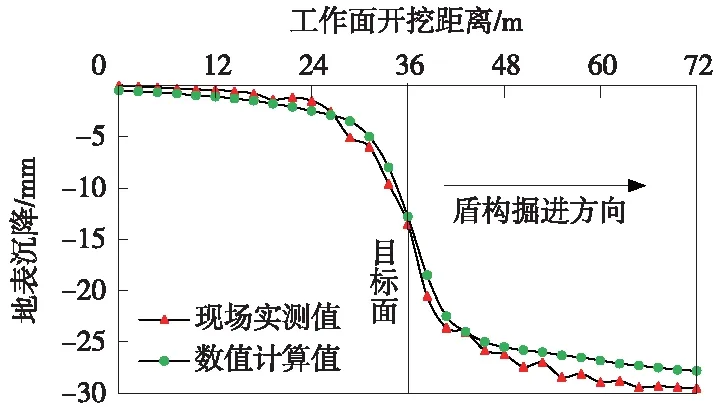
图4 目标面地表沉降随开挖面推进变化曲线

由图4可以看出，数值计算结果与现场实测值基本一致，在开挖面到达目标面之前一定距离内，目标面处地表已经发生沉降，随着开挖面接近→通过→远离目标面，地表沉降急剧增大。在开挖面通过监测断面S2前，实测地表沉降最大值为13.5 mm，占最终沉降变形的45%左右；数值计算地表沉降最大值为12.8 mm，占最终沉降变形的46%左右。

3 地表沉降的施工控制措施

厦门轨道交通2号线某区间隧道，最小埋深为13.2 m，覆土深度较小，施工对地表影响较大。此外，盾构施工主要在残积砂质黏土层中进行，由于该地层渗透性较大，且部分处于地下水中，随着地下水位波动(尤其是水位下降，孔隙水压力降低)对地表沉降有较大影响，从而对本区间段施工产生不利因素。因此，需要制定相应的地表沉降控制技术措施。根据本文上节分析，结合现场施工条件，以同步注浆、土舱压力及推进速度为控制性因素，制定合理的沉降控制措施。

3.1 同步注浆改进

同步注浆是在盾构掘进施工的同时，由盾尾注浆管注入，同步注浆是否饱满，对控制地表最终沉降极其重要。为了减小盾构施工引起的地层损失和应力释放率，控制地表沉降，应该在地表沉降量较大的区段适当增加注浆量。为确定合适的注浆量，采用三维数值模型模拟注浆时，假定盾构施工引起的土体损失沿洞周分布均匀，损失率为3%，将注浆层等效为分别作用在洞周土体和管片上的均布压力，将同步注浆量分别设置为2.4，2.6，2.8，3.0 m3。通过三维数值计算，所得最终沉降量与注浆量的关系如图5所示。

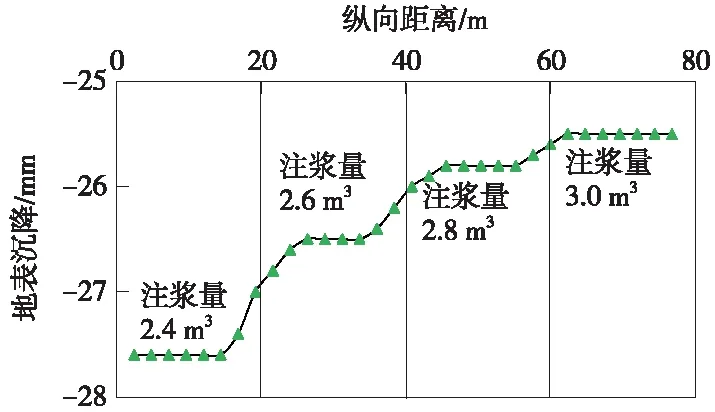
图5 不同注浆量对应地表最终沉降曲线

从图5可以看出，当注浆量从2.4 m3增加到2.6 m3时，地表沉降减小1.1 mm；注浆量增加到2.8 m3时，地表沉降减小0.7 mm；当注浆量为3.0 m3时，地表沉降减小0.3 mm。随着每环同步注浆量从2.4 m3提高到3.0 m3，地表最终沉降为25.5 mm，减小了2.1 mm。因此，增加注浆量在一定程度上改善了地表沉降问题，注浆量从2.4 m3增加到2.8 m3，地表沉降减小了6.5%，建议施工时注浆量为2.4～2.8 m3。同时，对浆液进行改良，以减小其凝固时间和凝固后的体积收缩率。

3.2 土舱压力设定

盾构机土舱压力值的设定，不仅直接影响盾构施工的安全、效率，同时也是地表沉降量的控制因素之一。为维持开挖面稳定，减少对土层的扰动，可以适当提高土舱压力值，减小开挖面的挤出变形。在三维数值计算中，充分考虑土舱压力，模型中分别设置土舱压力为0.12，0.15，0.18 MPa和0.21 MPa，每次开挖1环(1.2 m)，具体操作过程如下：①为了使模拟更接近实际情况，将第n环分为6小段，逐段开挖；②在开挖第n环的每一小段之前，在第n环每一小段开挖面施加土舱压力；③开挖第n环后，相应地，激活第n环管片及等效注浆层。基于上述三维数值模拟方法，设置不同的土舱压力值，对盾构开挖过程中的地表沉降动态过程进行计算，得到结果如图6所示。

图6 不同土舱压力下地表动态沉降曲线

根据图6显示，随着土舱压力从0.12 MPa(初始设计值)增加到0.21 MPa，施工过程中目标面处对应的地表沉降共计减小4.3 mm；盾构施工完成后，地表最终沉降减小2.5 mm。随着开挖面推进，地表沉降动态变形趋势基本相同，但开挖面到达目标面之前，伴随土舱压力提高，地表沉降有推迟趋势。当土舱压力为0.21 MPa时，在开挖面通过目标面初期，沉降量反而大于0.18 MPa时的沉降量，这是由于开挖面土压力不平衡造成的。由此可以看出，适当提高土舱压力值，在一定程度上可以控制地表沉降的发展。土舱压力从0.12 MPa提高到0.18 MPa，地表沉降减小6.1%，据此，当土体侧压力系数为0.6时，建议土舱压力在0.12～0.18 MPa调整，以确保开挖面稳定和土压力动态平衡。

3.3 推进速度控制

盾构推进系统应该根据掘进过程中所处的不同地层、地下水位变化，设定合理的推进速度，以减少对周围土体的扰动，减缓盾构开挖引起的应力重分布速度，使盾构在掘进过程中引起的地表沉降量控制在要求范围内。龚国芳[30-31]利用Matlab软件，建立基于BP神经网络的盾构推进速度仿真模型，通过神经元学习，从而实现盾构掘进机推进速度的自适应控制；刘镇[32]根据弹性力学Mindlin解，建立了盾构穿越邻近土洞的力学模型，以推进速度为控制变量，利用梯度法求解了最优掘进速度，并且该方法与工程经验拟合较好。可以借鉴上述方法，考虑不同地层、埋深、间距等条件，对盾构掘进速度进行优化。此外，文献[17]提出了一种较简单的方法，可以根据现场地表沉降监测提供的数据，放慢推进速度或者每推进半幅(0.6 m)，暂停15～30 min，待变形稳定后继续推进。

3.4 地表沉降的综合控制分析

在实际工程中，同步注浆、土舱压力及推进速度等参数总是同时作用、共同影响着地表沉降。但是，盾构机的推进是连续的，在数值分析中，通过改变土体单元的属性来模拟隧道的开挖，不能体现盾构隧道掘进的连续性，可以采用BP神经网络[31]、变量优化[32]等方法实现推进速度控制。鉴于此，本文仅研究同步注浆和土舱压力参数同时作用时的地表沉降情况。在数值模型中，分别以土舱压力和同步注浆量为定值，计算不同注浆量和不同土舱压力对应的地表沉降。根据计算结果，当同步注浆量为定值时，提高土舱压力对地表沉降的影响不如以土舱压力为定值、增加注浆量时显著。因此，绘制土舱压力为0.15 MPa，注浆量为2.4，2.6 m3和2.8 m3时S1断面处的地表最终沉降曲线，如图7所示。

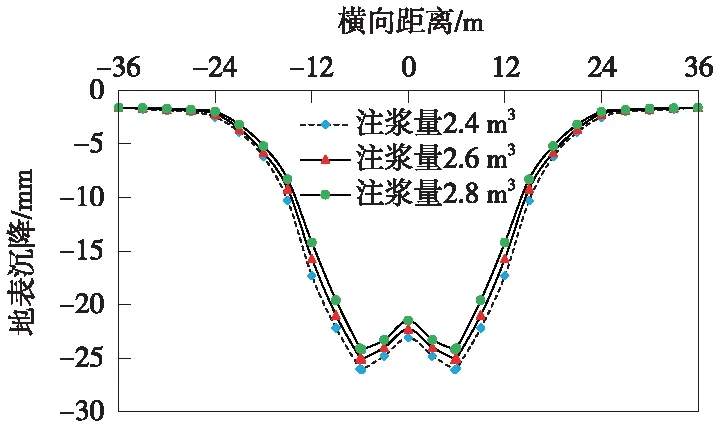
图7 土舱压力为0.15 MPa时不同注浆量对应的地表最终沉降曲线

由图7可以看出，土舱压力和同步注浆参数同时作用时，地表沉降的变化主要表现在两个方面：一是随着注浆量增加，地表最终沉降呈减小趋势，注浆量从2.4 m3增加到2.8 m3时，地表最终沉降累计减小量为1.9 mm，减小了7.3%，与未考虑土舱压力时(图5)相比，沉降控制效果有所提升，但地表沉降的累计减小量小于土舱压力和同步注浆参数分别作用时的简单叠加；二是增加注浆量，对隧道轴线处地表沉降的控制效果更加显著，在横向距离较远处，地表沉降几乎无影响。综上所述，土舱压力和同步注浆参数共同作用时，对地表沉降的控制效果不如上述参数单独作用时显著。因此，从工程造价和工程的长期运营稳定性方面来看，保持设计方案中的初始土舱压力(0.12 MPa)的同时、增加注浆量应该作为地表沉降控制的首选措施。