一种曲线无背索斜拉桥设计与计算
2019-07-26周昱
周 昱
(广州市市政工程设计研究总院有限公司 广州 510600)
0 引言
随着我国经济快速发展,人们生活水平提升,城市桥梁设计除满足交通功能性需求外,对桥梁自身的景观性需求也逐渐提高[1]。独塔无背索斜拉桥造型较为独特,常应用于城市景观桥梁。无背索斜拉桥通过桥塔重力平衡拉索拉力,整体结构受力较为复杂,索塔根部受力较为不利[2-4],多采用自重较大且较为刚性的混凝土桥塔,且多为墩塔梁固结的结构体系。
有别于常规无背索斜拉桥,东湾大桥平面位于道路圆曲线上,且出于对造型及施工工期的考虑,采用了钢桥塔并采用塔梁固结墩梁分离的结构体系[5]。本文对该桥的设计方案进行了介绍,并采用有限元方法建立全桥梁格模型和关键局部构件的板单元模型,对该桥全桥及局部受力进行了分析,分析结果可为今后的无背索斜拉桥设计计算提供参考指导。
1 工程概况及设计简介
1.1 总体布置
东湾大桥为空间拱形钢塔双索面无背索斜拉桥,全长146 m,跨径组合(106+40)m,桥梁平面位于R=1 800 m 的圆曲线上。桥梁为2 跨连续塔梁固结体系,塔身和主梁均为钢结构。桥型立面布置如图1所示。桥宽47.7 m,横向布置双向8 车道和2 人行道,并在中央设置管线走廊,如图2所示。

图1 斜拉桥总体布置图Fig.1 Cable-stayed Bridge Overall Layout(m)
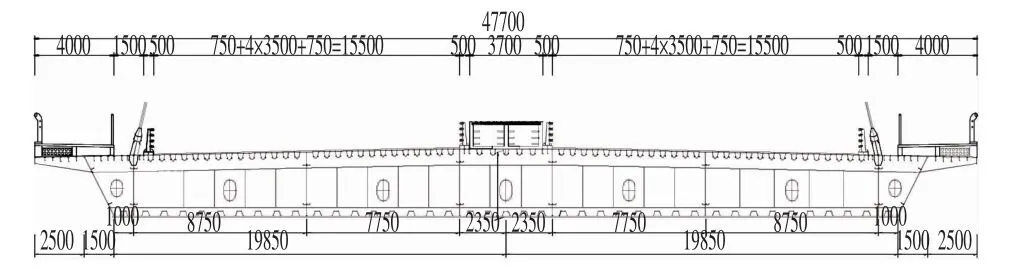
图2 钢箱梁截面Fig.2 Steel Box Beam Section
1.2 主梁设计
主梁为等截面钢箱梁,梁高3.038~3.338 m。标准段全宽47.7 m。钢箱梁为单箱多室截面,纵向设置8 道腹板。单侧翼板宽度为2.5 m,外腹板为斜腹板。桥面为正交异性钢桥面板,采用U 型加劲肋。为解决正交异性钢桥面固有的典型病害问题,提高钢桥面耐久性,桥面设置了8 cm STC 组合桥面层。由于桥梁不等跨布置,在靠近边支座处的钢箱梁内部设置压重混凝土。
1.3 桥塔及拉索设计
桥塔为变截面倾斜拱形结构,塔身立面后倾24.8°。桥塔纵桥向为变截面,底宽3.5 m 渐变到顶宽1.5 m。横桥向塔身底宽为2.5 m,塔身横向向顶部逐渐靠拢,顶部汇合成整体。塔身钢板厚度为28~40 mm,主塔截面如图3所示。从桥面算起,桥塔塔高为46.5 m。塔身下部与主梁固结,形成稳定的框架体系,桥塔立面如图4所示。
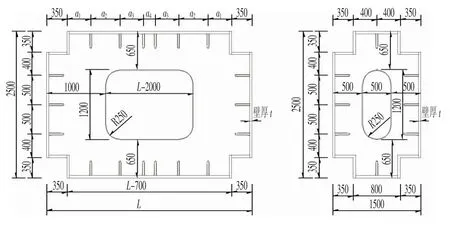
图3 主塔截面Fig.3 Cross Section of the Tower
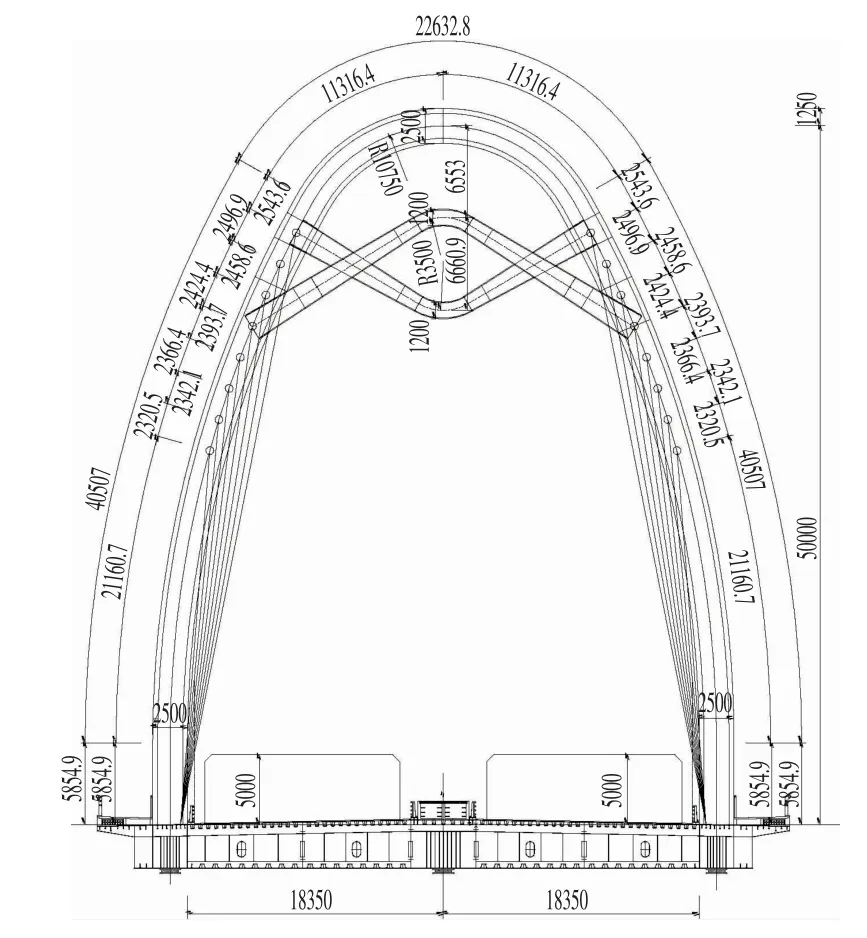
图4 桥塔处横断面Fig.4 Cross Section at the Tower(mm)
拉索与主梁夹角为20°~38.9°,在梁上的束距为9 m 共8 对。拉索采用整束挤压式钢绞线,在索塔端用插销式锚,在主梁端采用冷铸锚。
2 全桥静力分析
全桥模型采用有限元软件Midas 建立,如图5所示。主塔及塔间支撑采用梁单元模拟,斜拉索用桁架单元模拟,其余部件均采用板壳单元进行模拟。各部位边界条件,根据结构实际情况采用一般支承、弹性连接、刚性连接进行模拟。全桥整体结构静力分析采用的作用工况如下:[工况1]一期恒载+二期恒载;[工况2]恒载+汽车荷载+人群荷载;[工况3]恒载+移动荷载+系统升温;[工况4]恒载+移动荷载+系统降温;[工况5]恒载+移动荷载+梯度升温;[工况6]恒载+移动荷载+梯度降温。

图5 全桥模型Fig.5 FEM Model of the Bridge
2.1 变形验算
无背索斜拉桥通过倾斜主塔的自重平衡主梁荷载,特殊的结构体系决定了该桥型复杂的力学性能。本桥为高次超静定结构,按照设计规范需要验算整体结构的变形是否满足要求,其中桥塔变形为设计的控制条件。
对于本桥,由于采用了较为柔性的钢桥塔及梁高较大且较为刚性的主梁,故限制了拉索内力,使其分担较少的荷载,从而达到限制桥塔纵向位移的目的。计算分析结果也印证了这一设计意图;各荷载工况下的塔顶竖向和纵向位移如表1所示。在恒载作用下,主塔最大纵向位移为479 mm,如图6所示。
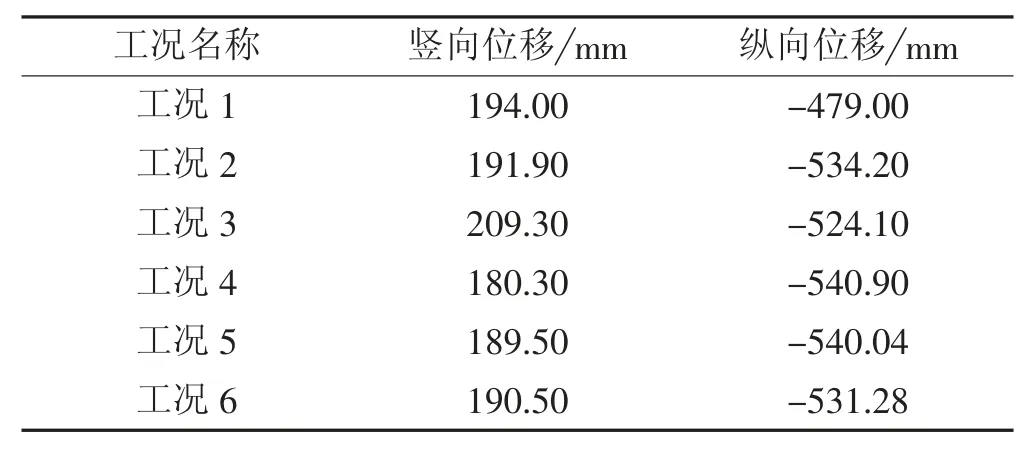
表1 不同荷载工况下的塔顶位移Tab.1 Displacement of Tower under Load Conditions
主梁在移动荷载、系统升温、系统降温、梯度升温、梯度降温作用下的竖向位移分别为-85.8 mm、-1.4 mm、0.9 mm、18.8 mm、-9.4 mm。在移动荷载作用下,主梁跨中最大竖向位移为85.8 mm,如图7所示,远小于设计限值:L/400=106m/400=265 mm。由计算结果可知主梁梁高较高,结构刚度较大。
2.2 弯矩验算
本桥通过倾斜主塔利用其自重在塔梁固结点产生的倾覆力矩与单侧斜拉索张拉力矩相平衡。因此,对主塔根部塔梁固结点实现力矩平衡是无背索斜拉桥的基本设计理念[6]。全桥受力情况如图8所示。
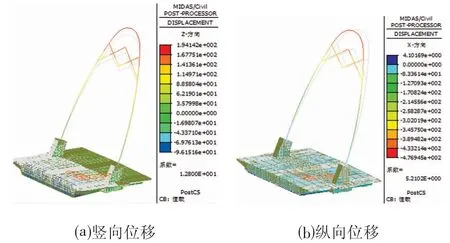
图6 主塔纵向位移Fig.6 Longitudinal Displacement of the Main Tower

图7 主梁竖向位移Fig.7 Vertical Displacement of the Main Beam

图8 结构静力平衡示意图Fig.8 Overall Structural Balance
为达到静力平衡,理想状态下主塔根部仅受轴力,为轴心受压状态,此时对于主塔固结点恒载产生的弯矩应满足下式[7]:

式中:ML为拉索区主梁对塔梁固结点的张拉力矩,ML=GL×LL;MT为主塔的自重对塔梁固结点的抵抗力矩,MT=GT×LT;GL为拉索区主梁自重;LL为主梁重心到固结点的力臂;GT为主塔自重;LT为主塔重心到固结点的力臂。
选取主跨跨中截面(1#),塔根过渡段(2#)、(3#),1/3 塔高处截面(4#)和塔顶(5#)等几个关键截面内力进行分析,关键截面在全桥中的位置示意图如9 所示,结果如表2所示。

图9 关键截面示意图Fig.9 Schematic of the Key Section
由于采用了塔梁固结,墩梁分离的结构体系;桥梁整体受力近似于连续梁,桥塔及拉索起到一个对梁进行“加劲”的作用。由计算结果亦可以看出主梁为主要受力构件,且控制弯矩中恒载占了很大比重。在梁跨中有较大的正弯矩,在2#桥墩处有较大的负弯矩。而桥塔在1/2 塔高截面和塔顶截面受弯矩较小。拉索可明显减小梁跨中弯矩,故梁受力控制点为塔梁结合处的负弯矩区。由于钢桥塔刚度较低,且较为轻巧,应控制其最大弯矩以避免产生过大变形;即位移控制桥梁设计,所以拉索张拉力不宜过大。全桥为“刚梁柔塔”的受力特点,这与内力分析结果也相吻合,全桥结构能保证较好的静力平衡。
2.3 强度验算
在投入正式运营后,桥梁结构体系应满足在最不利荷载组合作用下,所受应力要远小于材料的容许应力,结构强度要满足规范要求[8]。通过Midas 静力分析,结果如表3所示。
在最不利组合作用下,东湾大桥主跨主梁的最大应力为182 MPa,最小应力为116 MPa,主梁最大应力位于主跨0.4L 处截面,如图10所示。边跨主梁的最大应力为138 MPa,最小应力为91 MPa,位于边跨塔梁结合过渡段截面。塔梁结合部位的最大应力为192 MPa,最小应力104 MPa。主塔的最大应力为164 MPa,最小应力为137 MPa,位于主塔根部,如图11所示。钢结构的最大等效应力为225 MPa,位于塔梁结合位置的加劲板中。以上应力均小于16~40 mm 厚Q420d 钢强度设计值320 MPa,因此钢结构的应力强度满足规范要求。

表2 关键截面弯矩Tab.2 Bending Moment of Key Section(kN·m)
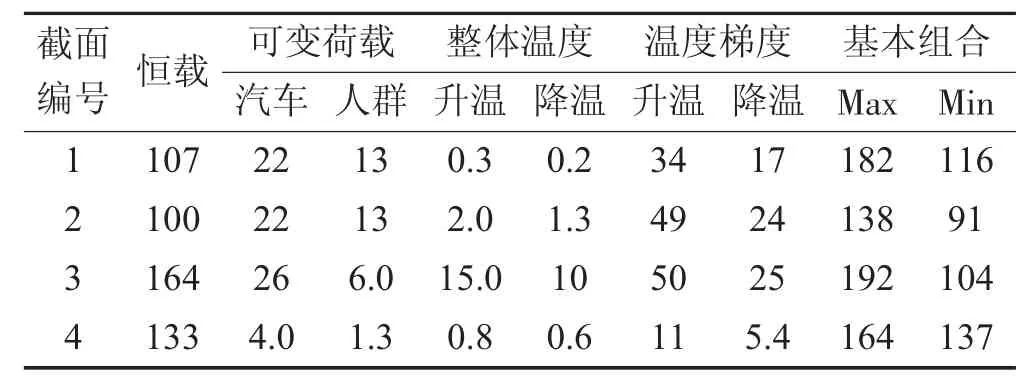
表3 关键截面应力Tab.3 Stress of Key Section(MPa)

图10 主梁轴应力Fig.10 Axial Stress of the Main Beam

图11 主梁横截面应力Fig.11 Cross-section Stress of the Main Beam
2.4 整体稳定性计算
本桥的结构稳定性计算同样采用空间有限元法进行,结构的静力稳定性分析计算模型与结构动力特性分析计算模型相同。计算时,考虑结构本身自重并在桥面施加活载,结构的稳定安全系数应按照下式计算[9]:

式中:Pcr为结构的极限承载力;PT为成桥状态的结构自重与活载之和,实际上K 是结构达到极限承载力时关于PT的加载倍数。
失稳模态图如图12所示,计算结果为该桥成桥状态下的一阶稳定系数为264.4,为主塔的面外失稳,可见屈曲稳定系数较大,桥梁整体稳定性较好。
3 局部静力分析
3.1 主梁锚拉板

图12 一阶失稳模态Fig.12 First Order Instability Mode
本桥采用锚拉板的构造形式连接拉索与主梁,锚拉板构造如图13a 所示。此处结构刚度变化大,局部受力复杂,为充分考察锚拉板的受力状态,采用有限元分析软件ANSYS15.0 板单元分析模型进行局部分析。模型采用Shell63 单元,板块厚度按结构实际尺寸,在模型底部施加固结约束。根据全桥分析结果,以在基本组合最大拉索力681 kN 为计算荷载。
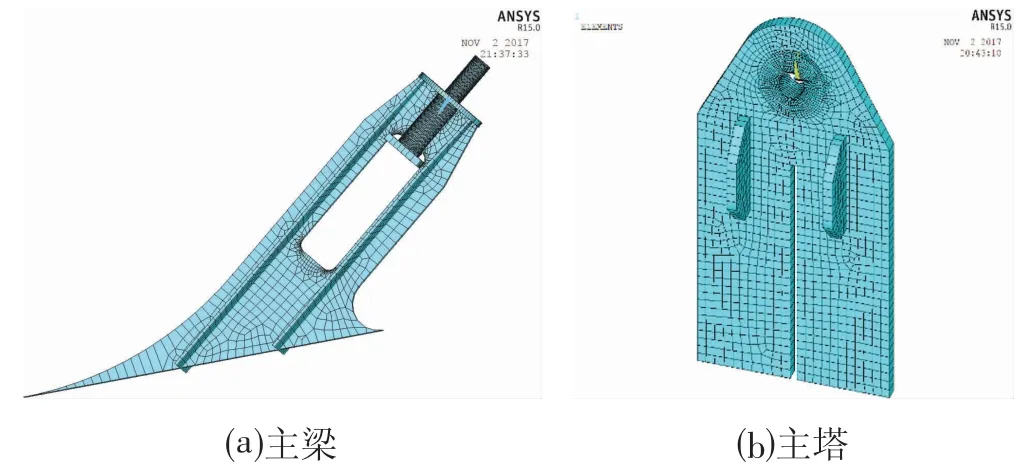
图13 锚拉板整体模型Fig.13 FEM Model of Anchor Plate
锚拉板最大位移为拉索方向-0.013 1 mm,最大总位移为0.480 mm,如图14a 所示。可见变形较小,满足设计要求。

图14 锚拉板最大总位移Fig.14 Maximum Total Displacement of Anchor Plate(m)
锚拉板第一主应力为137 MPa,如图15a 所示,第二主应力为-127 MPa,第三主应力为-163 MPa,von-Mises 应力为355 MPa。最大应力不超过材料容许应力值,锚拉板强度满足设计要求。
3.2 塔锚拉板
选取主梁受力拉索对应主塔锚拉板进行分析,其构造如图13b 所示。采用Shell63 单元,按结构实际板厚,在两加劲肋水平中心线处固结约束,以在基本组合最大拉索力681 kN 为计算荷载。

图15 锚拉板第一主应力Fig.15 First Main Dtress of Anchor Plate(MPa)
主塔锚拉板的 X、Y、Z 方向最大位移分别为-0.097 5 mm、0.082 9 mm 和-0.029 3 mm,最大总位移为0.122 mm,如图14b 所示。可知主塔锚拉板局部位移较小满足设计要求。
锚拉板垫板第一主应力最大值为160 MPa,如图15b 所示,第二主应力最大值为-68.7 MPa,第三主应力最大值为-78.5 MPa,von-Mises 应力为288 MPa,最大应力均不超过材料容许应力值,锚拉板强度满足设计要求。
4 动力特性分析
采用Lanczos 法对桥梁进行动力特性分析,提取前四阶振型如图16所示。第1 阶振型为一阶竖弯,频率0.902 Hz;第2 阶振型为一阶纵弯,频率1.521 Hz;第3 阶振型为一阶扭转,频率1.934 Hz;第4 阶振型为一阶横弯,频率2.034 Hz。本桥一阶振型自振周期较长,体现该桥整体较柔、结构轻巧这一特性,这对于抗震是有利的[10,11]。

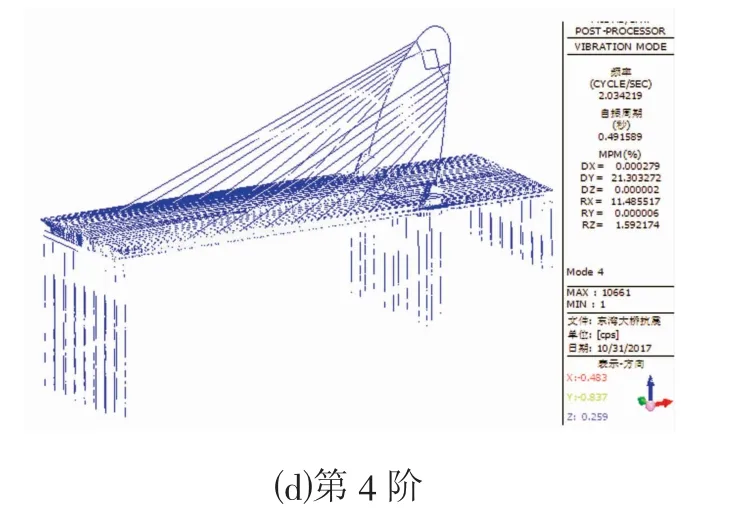
图16 全桥前四阶振型Fig.16 The Top Four Vibration Mode of the Whole Bridge
5 结论
结合东湾大桥实际工程,介绍了一种曲线无背索斜拉桥的桥梁设计;并通过全桥梁格及局部板单元的有限元分析模型对该桥进行了全桥动、静力分析及局部受力分析。通过计算结果分析了该桥的受力特点,并验算证实该桥设计安全合理。相关的设计经验及计算结果,可为该类桥梁设计提供一定参考。
