黄土丘陵区典型植被土壤剖面的颗粒分形特征①
2019-07-26马文芳朱云鹏郭倩倩党亚爱
马文芳,朱云鹏,郭倩倩,党亚爱
黄土丘陵区典型植被土壤剖面的颗粒分形特征①
马文芳,朱云鹏,郭倩倩,党亚爱*
(西北农林科技大学理学院,陕西杨凌 712100)
运用分形理论研究陕北安塞五里湾流域5种典型植被0 ~ 200 cm土壤剖面土壤颗粒大小分布(particle size distribution,PSD)及其体积分形维数分布特征,并进一步分析土壤PSD的分形维数与土壤有机碳、全氮和含水量的相关性。结果表明:研究区典型植被群落土壤颗粒组成主要为细颗粒(黏粒和粉粒),其中粉粒体积分数占总颗粒的56.82% ~ 71.99%;铁杆蒿草地的细颗粒平均体积分数最大(78.86%),乔木林的最小(65.77%)。5种典型植被群落土壤PSD的体积分形维数介于2.498 ~ 2.599,均表现出随着土层深度的增加呈递增趋势;相同土层深度的分形维数呈现出铁杆蒿草地>黄芪草地>农田>灌木林>乔木林的趋势,灌木林和农田间差异不显著,其他植被群落间差异显著。典型植被土壤PSD的体积分形维数与黏粒、粉粒的体积分数和含水量呈极显著正相关(<0.01),但与砂粒的体积分数呈极显著负相关(<0.01),与有机碳含量呈显著负相关(<0.05)。
黄土丘陵区;典型植被;土壤剖面;土壤PSD;体积分形维数
土壤颗粒大小分布(particle size distribution,PSD)影响着土壤水力特性、生产力以及土壤侵蚀等,是重要的物理特性之一[1-2],因此描述土壤PSD的变化是理解和量化土壤结构和动力特性的一种重要方法[3-5]。分形理论是用来描述不规则构型和自相似特点的有用工具[6],在土壤科学领域,该理论为研究者提供了一个既可描述又能预测土壤特性的途径,尤其在一定时空尺度内,提供了集土壤生物、化学和物理现象于一体的独特定量化结构。自从Tyler和 Wheatcraft[7-8]提出PSD的体积分形维数计算公式,分形理论在土壤学研究领域得到了广泛的应用。近年来,许多研究者利用分形理论描述土壤 PSD、孔径分布和团聚体粒径分布等以评价植被对土壤结构、土壤侵蚀性和渗透性的影响[9-12],相关研究发现土地利用变化和植被类型显著影响土壤分形参数[13-14],且土壤PSD的分形维数与土壤颗粒组成及土壤肥力关系密切,但结果不尽相同[15-17],仍存在一定争议。
黄土高原丘陵区沟壑纵横,梁峁坡地分布广泛,自然植被曾遭到严重破坏,土壤结构疏松,是中国水土流失严重的地区之一[18-19]。为减少黄土高原水土流失,中国政府实施了大面积的退耕还林(草)工程,形成了不同立地条件及不同年限的植被[20]。安塞五里湾流域是黄土高原丘陵区典型侵蚀流域之一,该区域自退耕还林(草)工程实施后,植被恢复使得水土流失得到明显改善,但是不同植被类型对土壤结构及养分含量等的影响目前仍存在一定的不确定性,且土壤剖面颗粒分布的变化趋势鲜有报道。本文以安塞五里湾流域典型植被土壤剖面为研究对象,揭示不同植被类型和土层深度下土壤颗粒大小分布及其分形维数的变化趋势,探索分形维数与土壤有机碳、全氮和含水量的相关性,研究结果为黄土丘陵区进一步植被恢复方针政策制定、区域土地资源可持续利用提供一定的理论依据。
1 材料与方法
1.1 试验区域概况
采样点位于陕西省延安市安塞县境内的五里湾流域(图1)。该区域属于暖温带半干旱气候区,海拔853 ~ 1 338 m,年均气温6 ~ 10 ℃,年降雨量340 ~ 600 mm,主要集中在7—9月,蒸发量远大于降雨量。黄土塬梁丘陵沟壑地貌,黄绵土为主,水土流失严重。植被地带属森林草原带,天然林较少,主要以“退耕还林(草)”工程实施后的人工林为主,目前主要植被有刺槐()、侧柏()、山杏()、柠条()等,铁杆蒿()、茭蒿()、黄芪()、达乌里胡枝子()等。
1.2 野外采样
2016年8月在延安市安塞五里湾流域选择典型的铁杆蒿草地、黄芪草地、农田、乔木林和灌木林进行采样。每块样地选3个平行样点取样,用土钻分别采集0 ~ 10、10 ~ 20、20 ~ 40、40 ~ 60、60 ~ 80、80 ~ 100、100 ~ 120、120 ~ 140、140 ~ 160、160 ~ 180、180 ~ 200 cm土层土样,带回实验室进行分析。样地自然特征如表1所示。

图1 研究区域及样地分布图
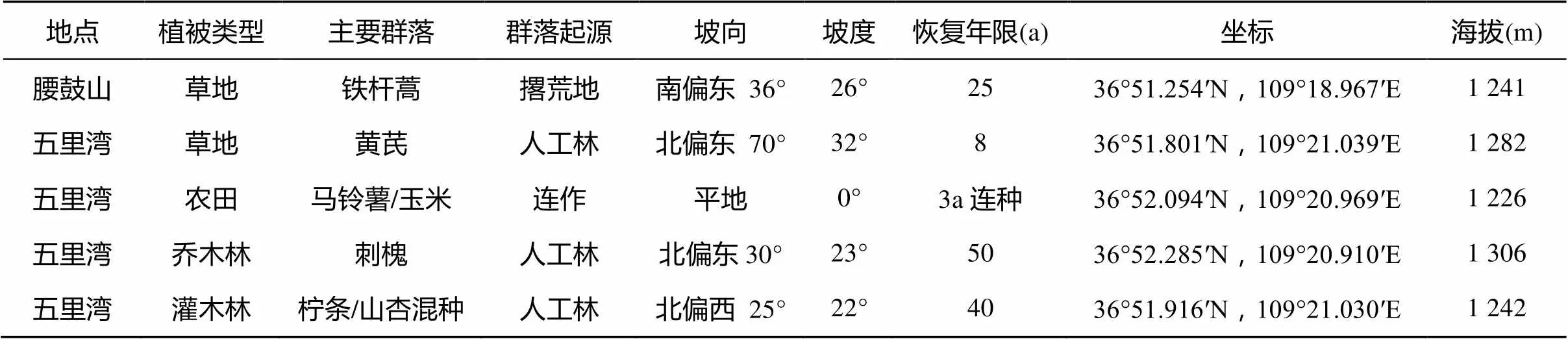
表1 样地的自然特征
1.3 室内分析
用烘干法测量土壤含水量,其余土样风干、研磨、过筛、备用。颗粒分布采用英国马尔文公司的MS2000型激光粒度测量仪测定。根据美国土壤质地分类系统,将土壤粒径分为0 ~ 0.002、0.002 ~ 0.05、0.05 ~ 0.1、0.1 ~ 0.25、0.25 ~ 0.5和0.5 ~ 1 mm 6个级别,其次根据美国制分类标准分为黏粒(<0.002 mm )、粉粒(0.002 ~ 0.05 mm)和砂粒(0.05 ~ 1 mm)。土壤有机碳测定用重铬酸钾容量法-外加热法;全氮含量测定用半微量凯氏定氮法[21]。
1.4 分形模型
利用激光粒度测量仪所获得粒径体积分数,当土壤粒径大于R(R>R1=1, 2, 3…)的土壤颗粒体积累积函数可以表示为:

式中:R为特征尺度,C和λ是用来描述土壤颗粒形状和大小的常量,是土壤PSD的单分形维数。当R= 0时,上式中的为所有土壤颗粒的体积分数T或C。当R=max、λ= 1 mm时,(1) 式可变形为:

式中::土壤粒径;:粒径大于R的土壤粒径总体积分数(%);T:为土壤颗粒总体积分数(%);max在数值上等于最大粒径数[14]。根据王国梁等[16]的研究将>的形式转化为<,得到

将(3)式等式两端取对数,为

最后将各粒级体积分数代入以上对数函数,作回归方程,得到的斜率即可求得土壤PSD的分形维数。
1.5 数据分析
5种植被类型土壤颗粒大小分布和土壤基本性质的数据均经过Excel软件进行处理,不同植被类型数据间的比较分析通过SPSS 20的多因素方差分析(ANOVA)完成,多重比较采用Bonferronl法,并采用Origin 8.1作图。


Eta方(Eta squared,2),又称关联强度(correlation ratio)即处理间平方和(SSbetween)除以总平方和(SStotal),表示由组间差异所解释的因变量的方差的比例。其计算公式如下:


2 结果与分析
2.1 典型植被土壤剖面的土壤颗粒大小分布(PSD)特征
安塞五里湾流域典型植被土壤PSD随土层深度的变化规律见图2。整体来看,该区域土壤粉粒体积分数最大,占总颗粒的56.82% ~ 71.99%;其次是砂粒,占16.77% ~ 36.39%;黏粒所占比例最小,为6.795% ~ 11.39%。除个别土层,草地、乔木林和灌木林的土壤细颗粒(黏粒和粉粒)体积分数整体上均存在显著性差异(<0.05),其中铁杆蒿草地土壤剖面的细颗粒平均体积分数最大(78.86%);乔木林的最小(65.77%)。5种典型植被土壤黏粒和粉粒的体积分数随着土层深度的增加均表现为递增趋势;相反,砂粒的体积分数随着土层深度的增加而递减。
2.2 不同植被类型土壤PSD的体积分形维数在土壤剖面的分布特征
多因素方差分析结果显示植被类型、土层深度和它们之间的交互作用对土壤PSD的体积分形维数具有极显著影响(<0.01)(表2)。其中典型植被类型和土层深度的偏Eta方均大于0.8,表示植被类型和土层深度均能很好地解释总体的变异,结果的可信度较高。
研究区域典型植被土壤PSD的体积分形维数随土层深度的分布特征如图3所示。从纵向看,5种植被下土壤PSD的体积分形维数均随着土层深度的增加而增大,且均在160 ~ 200 cm土层达到最大。但不同植被的土壤PSD体积分形维数在土壤剖面的变化幅度不同,其中铁杆蒿草地的变化幅度最大(2.519 ~ 2.599),变异系数为0.921%;乔木林的变化幅度最小(2.498~2.517),变异系数为0.243%。从横向看,相同土层典型植被土壤PSD的体积分形维数表现出铁杆蒿草地>黄芪草地>农田>灌木林>乔木林的趋势,其中灌木林和农田间差异不显著,其他典型植被群落间差异显著(<0.05)。铁杆蒿草地土壤剖面的平均体积分形维数最大(2.570),乔木林的最小(2.511)。

(图中小写字母不同表示同一土层不同典型植被间差异显著(P<0.05))

表2 典型植被类型和土壤深度对土壤PSD的体积分形维数影响的多因素方差分析结果
2.3 土壤PSD的体积分形维数与颗粒组成的相关性
土壤PSD的体积分形维数的大小与土壤颗粒分布密切相关,为了进一步揭示土壤PSD体积分形维数与颗粒组成的关系,分别对土壤体积分形维数与土壤黏粒(0 ~ 0.002 mm)、粉粒(0.002 ~ 0.05 mm)和砂粒(0.05 ~ 2 mm)的体积分数进行了相关性分析(图4)。结果表明,土壤PSD体积分形维数与黏粒和粉粒体积分数均呈极显著正相关关系(<0.01),而与砂粒含量呈极显著负相关关系(<0.01)。

(图中小写字母不同表示同一土层不同典型植被间差异显著(P<0.05))
2.4 土壤PSD的体积分形维数与土壤基本性质的相关性
研究区域典型植被土壤PSD体积分形维数与不同粒径颗粒的体积分数及土壤基本性质的相关分析见表3。可以看出,土壤PSD体积分形维数与黏粒、粉粒及土壤含水量均存在极显著正相关关系(< 0.01),与砂粒体积分数呈极显著负相关关系(< 0.01),与土壤全氮含量未达到显著水平,与土壤有机碳含量呈显著负相关(<0.05);土壤黏粒与上述土壤基本性质均达到显著或极显著相关关系。含水量与有机碳、全氮呈极显著负相关(<0.01),与粉粒和砂粒含量均未达到显著性水平。

图4 土壤颗粒体积分形维数与土壤颗粒大小分布(PSD)的相关性

表3 典型植被土壤PSD的体积分形维数与不同粒径土壤颗粒体积分数及土壤基本性质的相关性
注: ** 表示相关性达到<0.01显著水平,* 表示相关性达到<0.05显著水平。
3 讨论
土壤的PSD继承了母质的一定特征,并综合了土地利用及人为活动等环境变化的影响,是土壤本质属性之一[24-26]。本研究表明,植被类型、土层深度和它们之间的交互作用显著影响土壤PSD的体积分形维数(<0.01),这是由于成土母质、气候、地形、植被及人类干扰程度的差异,在一定程度上通过影响土壤水蚀和风蚀导致土壤PSD和土壤肥力变化,进而表现为不同植被类型和土层深度下土壤PSD的体积分形维数存在差异:在较大尺度上,土壤主要受母质、气候、地形等因子的控制;在较小尺度上,主要受土壤特性、植被覆盖、微立地以及人为干扰的影响。相同土层5种典型植被土壤PSD体积分形维数大小顺序与黏粒的体积分数大小顺序相似,均表现为铁杆蒿草地>黄芪草地>农田>灌木林>乔木林。Zuazo[27]研究表明植被覆盖和根系结构能促进土壤质地的改善,减少土壤颗粒及地上生物量的流失;王晗生和刘国彬[28]认为植被水土保持效果关键取决于贴地面覆盖及地表枯落物的数量和质量,其中贴地面覆盖植被的作用尤其重要。铁杆蒿草地和黄芪草地因能较为迅速地郁闭覆盖地面,贴地面生长,对土壤的修复作用优于长期不能郁闭、缺乏枯枝落叶层的人工林和农田[19];乔木林土壤砂粒含量较高,分形维数较低,可能是由于乔木林(刺槐群落)根茎直且分布较深,吸水性较强,土壤含水量下降,导致土壤结构疏松,孔隙度大,可能会加重风力侵蚀力度,而且土壤的干燥也会使荒漠化的进程加快。
土壤分形维数是反映土壤结构几何形状的参数,管光玉等[29]与程冬兵等[30]认为,土壤颗粒分形维数越高,土壤质地越细,表征土壤结构越紧实,通透性越差;分形维数越小,则土壤质地相对松散,通透性较好。本研究发现5种典型植被土壤细颗粒(黏粒和粉粒)的体积分数和土壤PSD的体积分形维数均随着土层深度的增加而增大,且在160 ~ 200 cm土层达到最大值。一方面反映了土壤母质的特点;另一方面可能土壤表层由于风蚀和水蚀,土壤细颗粒遭到一定量的流失,土壤质地较深层松散;另外,也可能与土壤颗粒的淋溶下移有关[31]。本研究结果与Xiao等[9]对黄土高原纸坊沟流域不同土地利用方式下土壤剖面分形特征的研究一致;但与Yu等[32]发现黄河三角洲新成湿地表层土壤的分形维数大于下层土壤的研究结果有所区别,究其原因,主要由于新成湿地的土壤颗粒组成主要是砂粒,且土壤粗化严重。
本研究区域土壤PSD的体积分形维数与黏粒(<0.002 mm )和粉粒(0.002 ~ 0.05 mm)的体积分数呈极显著正相关关系(<0.01),与砂粒(0.05 ~ 2 mm)的体积分数呈极显著负相关关系(图4和表3),线性回归的决定系数变化范围为0.711 ~ 0.919,表明利用分形模型来评估典型植被土壤剖面的PSD是合理的。这与Chen等[33]对中国南方斜坡修复下土壤颗粒大小分布的分形特征和Niu 等[14]对中国北方山区不同植被类型土壤水分保持曲线和颗粒大小分布的分形特点研究结论相吻合,但与王国梁等[16]的研究结论即土壤颗粒分形维数与黏粒含量呈正相关,与粉粒和砂粒含量呈负相关有所区别,这可能与其研究区域的土壤质地和植被类型等有所差异有关。
本研究发现,土壤PSD的体积分形维数与全氮和有机碳含量均呈负相关,且和有机碳含量达到了显著负相关水平(<0.05)(表3)。这与谢贤健和韩光中[34]的研究结果即土壤体积分形维数与土壤有机质含量呈显著负相关较为一致,但与党亚爱等[25]研究发现黄土高原典型土壤剖面颗粒的体积分形维数与有机碳极显著正相关结果相反,可能是由于本研究区域的土壤颗粒组成主要为粉粒。
4 结论
1)植被恢复可直接或间接地影响土壤颗粒大小分布(PSD)及其体积分形维数;研究区域不同植被类型、相同土层深度土壤PSD的体积分形维数与黏粒的体积分数大小顺序相似,均表现为铁杆蒿草地>黄芪草地>农田>灌木林>乔木林,其中铁杆蒿草地土壤剖面的平均体积分形维数最大(2.570),乔木林的最小(2.511)。
2)土层深度对研究区域土壤PSD及其体积分形维数具有显著的影响,5种典型植被土壤细颗粒(黏粒和粉粒)的体积分数和土壤PSD的体积分形维数均随土层深度的增加呈增大趋势,且在160 ~ 200 cm土层达到最大值。
3)研究区土壤PSD的体积分形维数的变化范围为2.498 ~ 2.599,其与黏粒(<0.002 mm )和粉粒(0.002 ~ 0.05 mm)的体积分数呈极显著正相关(<0.01),与砂粒(0.05 ~ 2 mm)的体积分数呈极显著负相关(<0.01)。
4)土壤PSD的体积分形维数与土壤含水量呈极显著正相关(<0.01),但与土壤全氮和有机碳含量均呈负相关,且与有机碳含量达到了显著水平(< 0.05)。
[1] Giménez D, Perfect E, Rawls W J, et al. Fractal models for predicting soil hydraulic properties: A review[J]. Eng. Geol., 1997, 48: 161–183
[2] Rieu M. Fractal fragmentation, soil porosity and soil water properties: I. Theory[J]. Soil Science Society of America Journal, 1991, 55: 1231–1238
[3] Kravchenko A N, Boast C W, Bullock D G. Multifractal analysis of soil spatial variability[J]. Agron. J., 1999, 91: 1033–1041
[4] Gao G L, Ding G D, Wu B, et al. Fractal scaling of particle size distribution and relationships with topsoil properties affected by biological soil crusts[J]. PLoS One, 2014, 9(2): e88559
[5] Ghanbarian B, Daigle H. Fractal dimension of soil fragment mass-size distribution: A critical analysis[J]. Geoderma, 2015, 245: 98–103
[6] Turcotte D L. Fractal and fragmentation[J]. Journal of Geophysical Research, 1986, 91: 1921–1926
[7] Tyler S W, Wheatcraft S W. Application of fractal mathematics to soil water retention estimation[J]. Soil Science Society of America Journal, 1989, 53(4): 987–996
[8] Tyler S W, Wheatcraft S W. Fractal scaling of soil particle-size distributions: Analysis and limitations[J]. Soil Science Society of America Journal,1992, 56(2): 362–369
[9] Xiao L, Xue S, Liu G B, et al. Fractal features of soil profiles under different land use patterns on the Loess Plateau, China[J]. Journal of Arid Land, 2014, 6(5): 550–560
[10] Ahmadi A, Neyshabouri M R, Rouhipour H, et al. Fractal dimension of soil aggregates as an index of soil erodibility[J]. Journal of Hydrology, 2011, 400(3/4): 305–311
[11] Millán H, Orellana R. Mass fractal dimensions of soil aggregates from different depths of a compacted Vertisol[J]. Geoderma, 2001, 101(3/4): 65–76
[12] Xu Y F, Sun D A. A fractal model for soil pores and its application to determination of water permeability[J]. Physica A Statistical Mechanics & Its Applications, 2002, 316(s 1/2/3/4): 56–64
[13] Wang D, Fu B, Zhao W, et al. Multifractal characteristics of soil particle size distribution under different land-use types on the Loess Plateau, China[J]. Catena, 2008, 72(1): 29–36
[14] Niu X, Gao P, Wang B, et al. Fractal characteristics of soil retention curve and particle size distribution with different vegetation types in mountain areas of Northern China[J]. International Journal of Environmental Research, 2015, 12(12): 15379–15389
[15] 杨慧玲, 高鹏, 王华伟, 等. 大黑山生态修复区不同植被类型土壤颗粒的分形特征[J]. 中国水土保持科学, 2009, 7(5): 52–57
[16] 王国梁, 周生路, 赵其国. 土壤颗粒的体积分形维数及其在土地利用中的应用[J]. 土壤学报, 2005, 42(4): 545– 550
[17] 梁士楚, 董鸣, 王伯荪, 等. 英罗港红树林土壤粒径分布的分形特征[J]. 应用生态学报, 2003, 14(1): 11–14
[18] 张超, 刘国彬, 薛萐, 等. 黄土丘陵区不同植被类型根际土壤微团聚体及颗粒分形特征[J]. 中国农业科学, 2011,44(3): 507–515
[19] 赵护兵, 刘国彬, 曹青玉, 等. 黄土丘陵区不同土地利用方式水土流失及养分保蓄效应研究[J]. 水土保持学报, 2006, 20(1): 20–24
[20] Jiao J Y, Tzanopoulos J, Xofis P, et al. Factors affecting distribution of vegetation types on abandoned cropland in the hilly-gullied Loess Plateau region of China[J]. Pedosphere, 2008, 18(1): 24–33
[21] 鲍士旦. 土壤农化分析[M]. 3版. 中国农业出版社, 2000: 30–48
[22] 李春喜, 邵云, 姜丽娜. 生物统计学[M]. 4版. 北京: 科学出版社, 2008: 44–46
[23] Levine T R, Hullett C R. Eta squared, partial eta squared, and misreporting of effect size in communication research[J]. Human Communication Research, 2002, 28(4): 612–625
[24] 贾晓红, 李新荣, 李元寿. 干旱沙区植被恢复过程中土壤颗粒分形特征[J]. 地理研究, 2007, 26(3): 518–525
[25] 党亚爱, 李世清, 王国栋, 等. 黄土高原典型土壤剖面土壤颗粒组成分形特征[J]. 农业工程学报, 2009, 25(9): 74–78
[26] 王冬冬, 高磊, 陈效民, 等. 红壤丘陵区坡地土壤颗粒组成的空间分布特征研究[J]. 土壤, 2016, 48(2): 361–367
[27] Zuazo V H D. Soil-erosion and runoff prevention by plant covers. A review[J]. Agronomy for Sustainable Development, 2008, 28(1): 65–86
[28] 王晗生, 刘国彬. 植被结构及其防止土壤侵蚀作用分析[J]. 干旱区资源与环境, 1999(2): 62–68
[29] 管光玉, 范燕敏, 武红旗, 等. 不同利用方式土壤颗粒分形特征及其与土壤有机碳库稳定性的关系[J]. 草地学报, 2016, 24(2): 258–262
[30] 程冬兵, 蔡崇法, 彭艳平, 等. 根据土壤粒径分形估计紫色土水分特征曲线[J]. 土壤学报, 2009, 46(1): 30–36
[31] 高广磊, 丁国栋, 赵媛媛, 等. 生物结皮发育对毛乌素沙地土壤粒度特征的影响[J]. 农业机械学报, 2014, 45(1): 115–120
[32] Yu J B, Lv X, Bin M, et al. Fractal features of soil particle size distribution in newly formed wetlands in the Yellow River Delta[J]. Scientific Reports, 2015, 5: 10540
[33] Chen S N, Ai X Y, Dong T Y, et al. The physico-chemical properties and structural characteristics of artificial soil for cut slope restoration in Southwestern China[J]. Scientific Reports, 2016, 6: 20565
[34] 谢贤健, 韩光中. 不同巨桉人工林土壤分形特征及抗蚀性分析[J]. 土壤, 2014(4): 725–731
Fractal Characteristics of Soil Particle Compositions in Soil Profiles of Typical Vegetation Types on Loess Hilly Region
MA Wenfang, ZHU Yunpeng, GUO Qianqian, DANG Ya’ai*
(College of Science, Northwest A & F University, Yangling, Shaanxi 712100, China)
Based on fractal theory, the fractal characteristics of soil particle size distributions (PSDs) within 0-200 cm soil profiles of the typical vegetation types in Wuliwan Watershed on the Loess Hilly Region were studied to explore the effects of vegetation type and soil depth on soil structure and to explore the relations between the volume fractal dimension and the contents of soil organic carbon, total nitrogen and soil water. The results showed that soil particle composition was mainly fine particles (clay and silt), and silt particles approximately accounted for 56.82%-71.99% of the total volume. The average volume fractions of fine particles were 78.86% and 65.77% for soil profile ofgrassland and woodland, respectively. The fractal dimensions of soil PSDs in five typical vegetation types ranged from 2.498-2.599, and most of them increased with the depth of soil layer. At the same soil layer, the fractal dimension of soil PSD showed the following order:grassland>grassland>farmland>shrubland>woodland, But there was no significant difference between shrubland and farmland. The fractal dimension of soil PSD in typical vegetation had extremely significant positive correlation with water content and the volume percentage of clay and silt (<0.01), but significantly negative correlation with the volume percentage of sand and soil organic carbon content (<0.05).
Loess Hilly Region; Typical vegetation; Soil profile; Soil PSD; Volume fractal dimension
陕西省自然科学基金项目(2015JQ4107)和国家重点实验室专项基金项目(A314021402-1605)资助。
(dangyaai@126.com)
马文芳(1991—),女,河南许昌人,硕士研究生,主要从事土壤方面的研究。E-mail:mwfjiayou@163.com
S152.3
A
10.13758/j.cnki.tr.2019.03.022
