亚热带稻田土壤反硝化动力学参数估算①

邹刚华，赵凤亮，单 颖，李 勇

亚热带稻田土壤反硝化动力学参数估算①

邹刚华1，赵凤亮1，单 颖1，李 勇2*

(1中国热带农业科学院环境与植物保护研究所，海口 571101；2中国科学院亚热带农业生态研究所，长沙 410125)

反硝化作用是土壤氮素损失的重要途径，对反硝化潜势的准确估算是农业精准施肥的必然要求。以亚热带典型红壤稻田土作为研究对象，足量添加外源氮进行室内淹水厌氧培养获取反硝化作用动态，并分别用米氏方程和一级动力学方程对其拟合，最后利用土壤基本理化性质对反硝化动力学参数进行估算。结果表明：米氏方程更适合反硝化动力学拟合，最佳的米氏常数(m)为35 mg/kg；米氏最大速率常数(max)与一级动力学速率常数()具有显著的相关性(= 0.96,<0.05)。土壤总氮，砂粒和粉粒以及土壤容重对max影响最大。利用总氮和粉粒含量作为输入参数估算了max，准确度达66%。所构建的参数方程既充分挖掘了土壤基础数据潜能，又能快速地获取土壤反硝化动力学曲线，省时省力。

反硝化作用；酶动力学；红壤；参数估算；传递函数

氮素是植物生长必需和作物高产的重要因子，化肥的施用在提高作物产量同时，也产生了很多环境问题，如土壤酸化、土地板结、温室气体排放以及水体富营养化等[1-3]，如何提高农田氮素利用成为了农业精准施肥的瓶颈。过量氮肥输入除了造成氮素的浪费之外[4]，也加剧了氮素的转化损失[5]。其中，反硝化作用是农田氮素损失的重要途径之一，了解土壤潜在反硝化势是优化施肥的必要前提。

土壤反硝化作用受诸多因素影响，如影响酶反应速率的pH和温度、土壤质地以及底物浓度等[6]。当前研究反硝化依然以室内模拟为主，方法有乙炔抑制法和淹水培养法[7-8]，需要设置不同时间处理，费时费力。土壤传递函数是一类利用土壤基本理化性质来估算那些测定较为繁琐或获取较难指标的方法[9]。该方法在预测土壤水力学指标中应用较为广泛[10]，在反硝化动力学预测中罕见。基于此，本研究试图构建预测土壤反硝化作用的土壤传递函数。通过室内培养试验和土壤理化性质分析，并分别利用一级动力学和米氏方程积分式对反硝化作用进行拟合，确定模型参数，最后在相关性分析基础上，利用土壤基础性质来预测反硝化动力学参数，以期为快速地预测土壤反硝化潜势作参考。

1 材料与方法

1.1 研究区概况

研究区位于亚热带典型红壤区域湖南省金井镇，该地区经纬度：113°18 ~ 113°26′E，28°30 ~ 28°39′N，总面积210.8 km2，全区海拔50 ~ 430 m，属亚热带湿润季风气候，地形以丘陵、山地为主，为典型江南丘岗地貌。年平均气温17.2 ℃，年降水量1 200 ~ 1 500 mm，无霜期275 d，年日照时数1 663 h。研究区土壤类型以花岗岩和板页岩发育的红壤和水稻土为主，土地利用以林地和水田为主，占比分别为65.5% 和26.6%。林地分布于北部和丘岗之上，稻田主要分布在沟道内和河流两岸的冲击平原上。其中，稻田以双季稻为主，年平均产量12 500 kg/hm2。降雨和水库是农田主要水源，农田氮肥以尿素为主，平均用量375 kg/(hm2·a)。

1.2 样品采集与测定

依据研究区稻田的分布情况，用土钻采集了19个稻田0 ~ 20 cm表层混合土样，编号为S1，S2，…，S19，并同时分别取环刀样(100 cm3)。混合样于室内风干后，除去较大石块和植物残根后，过2 mm筛，然后用四分法取一部分样再过0.25 mm筛，用于测定土壤理化性质和后续的培养试验。土壤性质测定方法参照刘光崧[11]编著的《土壤理化分析与剖面描述》。土壤容重利用环刀法，即用环刀样于105 ℃下烘24 h测定。土壤pH采用pH计测定(土水比1︰2.5)。土壤机械组成(即砂粒、粉粒和黏粒)利用比重计法测定，粒径分布参照美国标准。土壤有机碳和总氮利用土壤碳氮分析仪(Vario MAX, Elementar, 德国)测定。

土壤反硝化动力学测定采用淹水厌氧连续培养法[8]。即称取10 g过2 mm筛的风干土样于100 ml的塑料浸提瓶中(3个平行)，加入25 ml 100 mg N/L(硝酸钾溶液)，添加的氮量为250 mg/kg 风干土，放置于25 ℃恒温室中分别培养0、1、3、5、7和9 d，然后于相应时间随机取出3个平行样，再加入25 ml 4 mol/L氯化钾浸提液，往返式振荡摇匀1 h，振荡速度为180 r/min，温度设置25 ℃，之后用中速定性滤纸过滤于50 ml塑料方瓶中，用流动注射分析仪(FIAstar5000, Foss, 瑞典)测定滤液中的NO– 3-N含量。

1.3 数据统计

分别利用米氏动力学方程积分式(Michaels- Menten kinetics)和一级动力学方程对土壤反硝化作用进行拟合，求得各动力学方程参数。曲线拟合优劣利用确定系数(2)判定，2越接近1，曲线拟合越好；越接近0，拟合越差。两方程的表达公式如下。

米氏方程：

其积分式为：

式中：为反应速率(mg/(kg·d))；为底物浓度(mg/kg)；max为最大反应速率(mg/(kg·d))；m为米氏常数(mg/kg)。为反应时间(d)；0和C分别为初始和时间的底物浓度(mg/kg)。

一级动力学方程：

式中：为一级动力学反应速率常数(d-1)。

通过分析米氏方程参数、一级动力学方程参数与土壤理化性质间的相关性，选取显著土壤性质，再利用多元线性逐步回归方法构建参数的估算方程，方程优劣利用确定系数判定。所有数据利用Excel 2007进行初步统计，米氏动力学方程及一级动力学方程拟合利用Excel软件中的规划求解功能计算出方程参数。利用R统计软件作相关性分析及绘图，并构建参数的回归方程。

2 结果

2.1 样品理化性质描述

19个土壤样品的基本理化性质见表1，总氮1.7 ~ 2.9 g/kg，均值2.3 g/kg；有机碳8.8 ~ 20.3 g/kg，均值14.3 g/kg；砂粒106 ~ 538 g/kg，均值为319 g/kg；粉粒299 ~ 684 g/kg，均值456 g/kg；黏粒155 ~ 310 g/kg，均值226 g/kg；容重1.12 ~ 1.46 g/cm3，均值1.32 g/cm3；pH 4.17 ~ 6.84，均值5.32。按粒径均值来考虑，土壤属于壤土质地，土壤pH偏低。从样品数据集的偏度来分析，所有性质都基本符合正态分布。

2.2 反硝化动力学拟合

土样反硝化动力学分别利用一级动力学和米氏方程积分式拟合，所有土样的拟合结果分别见图1和图2，其中相应的拟合参数值见表1。图1描述了土壤NO– 3-N含量随培养时间的动态变化，图2为米氏方程拟合中拟合时间和实测时间的线性图。一级动力学(指数方程)能较好地拟合大部分土样的反硝化作用，拟合的确定系数2范围为0.77 ~ 0.99，平均0.91；米氏方程拟合的确定系数范围为0.82 ~ 0.99，平均0.93，总体而言，米氏方程比一级动力学方程更适合反硝化动力学拟合。米氏方程中的参数包括最大速率常数max和米氏常数m，利用规划求解，本研究中发现米氏常数取固定值35 mg/kg时，可以获得最小的均方根差RMSE，基于此再分别估算样品的max，所得样品数据集max范围为17.6 ~ 90.2 mg/(kg·d)，平均46.1 mg/(kg·d)。一级动力学方程中的速率常数范围为0.074 ~ 1.505 d-1，平均0.48 d-1。同时，研究发现，米氏方程中的最大速率常数max与一级动力学方程中的速率常数有很高的相关性(图3)，相关系数为0.96，<0.01。两者之间完全可以用指数模型相互拟合估算(图3)，确定系数2为0.98，因此只需估算其中之一就能得知另一参数，本研究选择估算米氏方程中的最大速率常数max。

2.3 反硝化动力学参数方程

欲构建反硝化动力学参数估算模型，首先要得知其影响因素。一级动力学方程速率常数和米氏方程的最大速率常数与土壤理化性质间的相关性见图4。从图中看出，影响速率常数的因素包括土壤总氮(TN，= 0.54，<0.05)，粉粒含量(silt，= 0.59，<0.01)和土壤容重(BD，= –0.58，<0.01)。影响最大速率常数max的因子包括总氮、砂粒、粉粒以及容重，相比值，max受土壤总氮(= 0.68，<0.01)和容重(= –0.70，<0.01)影响更大。其他影响因子，如有机碳含量、黏粒以及土壤pH与和max相关性都不显著，因而后续建模不考虑。

表1 土样理化性质及反硝化动力学拟合参数

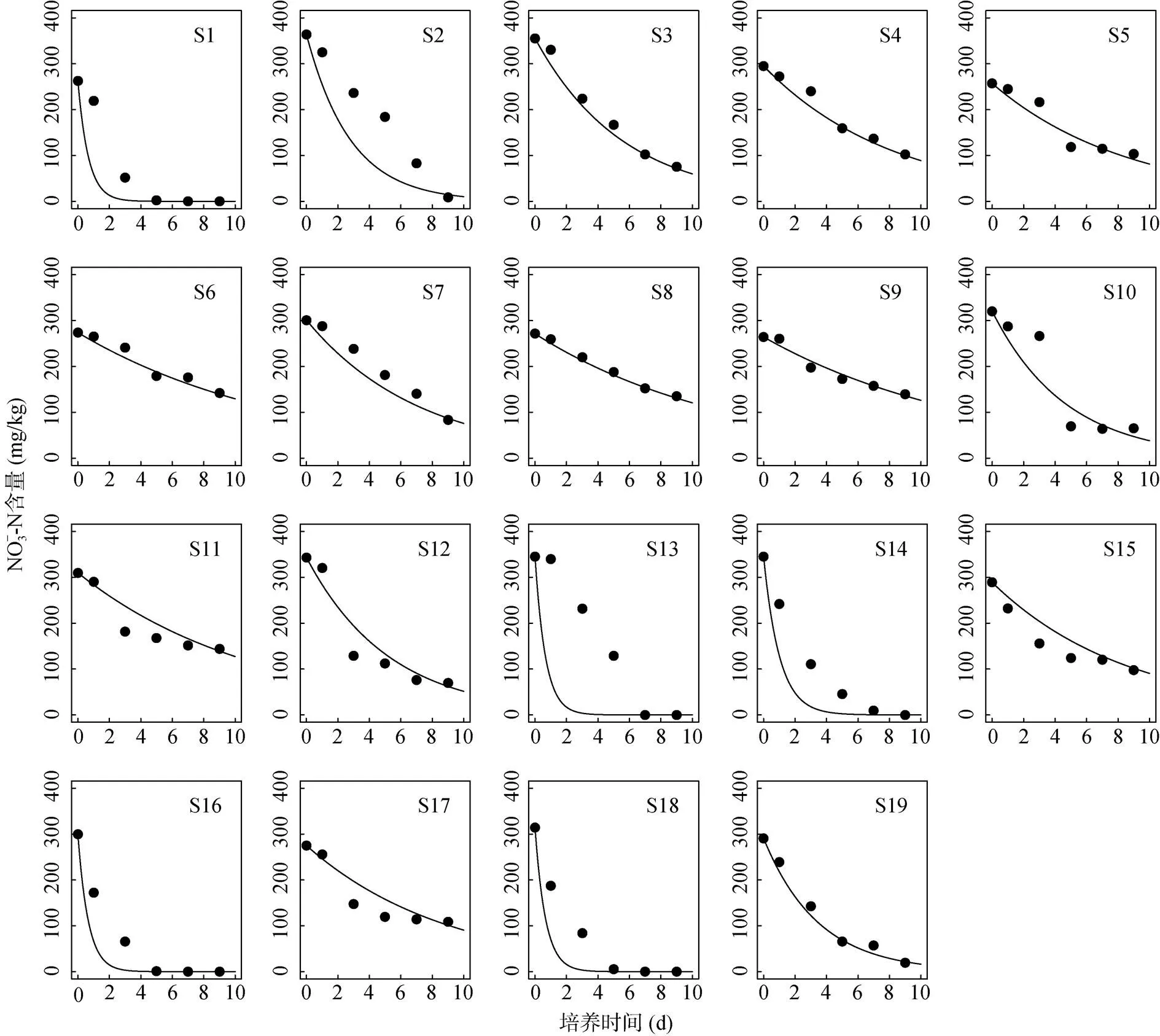
图1 一级动力学方程曲线拟合稻田土壤反硝化作用

图2 米氏方程拟合稻田土壤反硝化作用

图3 米氏方程最大速率常数(vmax)与一级动力学方程速率常数(K)曲线拟合

通过上述相关性分析，发现土壤总氮、容重以及质地中的砂粒和粉粒对最大速率常数max影响较大。然而，影响因素之间也存在显著的相关性，如总氮和容重(= –0.97，<0.01)，砂粒和粉粒(= –0.95，<0.01)，粉粒和容重(= –0.47，<0.05)。为避免模型中存在共线性，模型的输入参数之间不得有显著相关性。通过多元逐步回归方法分析，认为利用土壤总氮(TN)和粉粒含量(silt)就能获得可靠的模型拟合度，模型精度2达到0.66，相关估算方程见公式4，该模型对预测土壤反硝化动力学具有一定的参考价值。

ln(max)=5.98+0.89×ln(TN)+0.0017×silt(R=0.66，<0.001)(4)

式中：max为米氏方程中最大速率常数(mg/(kg·d))；TN为土壤总氮含量(g/kg)；silt为土壤粉粒含量(g/kg)。

(TN和SOC分别为总氮和有机碳(g/kg)；sand、silt和clay为土壤砂粒、粉粒和黏粒含量(g/kg)；BD为容重(g/cm3)；pH为土壤pH；vmax为米氏方程速率参数(mg/(kg·d))；K为一级动力学方程常数参数(d-1)；*表示相关性达到P<0.05显著水平，**表示相关性达到P<0.01显著水平)

3 讨论

厌氧条件下，微生物通过反硝化作用将土壤中的NO– 3-N还原成气态氮，从而造成了土壤氮素的损失。水稻种植期间，淹水创造了厌氧条件，土壤反硝化作用强烈。本研究通过室内淹水形成厌氧环境，添加足量外源氮保证底物充足来探讨稻田土壤的反硝化作用，设置温度为常温。研究发现，各土样呈现不同的反硝化能力，采集的19个土样中有5个样品NO– 3-N分解速率很快，几乎在5 d内就能全部降解。对于所有样品，一周之内，土样NO– 3-N平均能降解70%。指数方程(一级动力学)能很好地拟合大部分稻田土样的反硝化作用，最高的拟合度可以达到99%(如样品S3和S8)。刘培斌和郭亚洁[12]研究上海青浦稻田土壤时也认为，土壤NO– 3-N含量与培养时间基本符合一级动力学反应方程。然而本研究发现对有些反硝化作用强烈的土样，一级动力学拟合较差，如样品S13和S14，2分别为0.80和0.77，这表明一级动力学方程对稻田土壤反硝化动力学拟合还存在一定缺陷。再利用米氏方程对所有土样的反硝化动力学进行拟合，发现拟合能力有所提升，尤其是对反硝化速率较快的土样，如上述S13和S14的拟合精度分别提高到了0.92和0.97，同时也发现，对有些土样，米氏方程拟合精度也有所下降，如S12、S15和S17，精确度相比一级动力学拟合分别下降了7%、5% 和4%。综上分析表明，一级动力学方程和米氏方程各有所长，然而总体上米氏方程拟合更好。进一步分析两方程中的参数(速率常数和最大速率常数max)发现，两者存在显著相关性(= 0.98)，可以互换求解。

影响土壤反硝化作用的因素通常包括底物浓度(即NO– 3-N含量)、氧气含量、温度以及碳源等。本研究指定了培养温度和淹水厌氧条件，并且保证了充足的氮源，重点探讨土壤基本理化性质(如土壤有机碳、全氮、机械组成、容重和pH)对反硝化作用的影响。Ahn和Peralta[13]研究认为土壤性质对反硝化功能很重要。相关分析表明土壤总氮(= 0.68，<0.01)、砂粒(= –0.46，<0.05)、粉粒(= 0.58，<0.01)以及容重(= –0.70，<0.01)对反硝化作用影响显著；而土壤有机碳(= 0.44)、pH(= 0.09)则影响不显著(图4)。娄焕杰等[7]研究认为城市河岸带区农田背景下土壤反硝化速率与土壤有机碳和全氮含量为正相关，而与pH为负相关。反硝化作用需要底物氮，因此土壤全氮越高，底物氮也将越充足，反硝化速率加快；其次，反硝化作用需要能源物质，即有机碳，然而有研究认为有机碳含量增加，也可能会加快土壤氮素的固定[14]，从而减低了反硝化损失速率，Yu等[15]研究亚热带地区土壤反硝化作用时，认为反硝化速率与有机碳无关。土壤质地和容重反映了土壤的孔隙情况，过高的砂粒含量以及容重，不利于微生物代谢和活动，因此将降低反硝化速率。D’Haene等[16]研究比利时农田土壤不同深度反硝化作用及其影响因素时也发现，表层土壤反硝化势与质地有很大关系。土壤pH影响酶活性，随着pH升高至最佳值，土壤酶活性增强，微生物代谢也将增强，然而本研究却发现酸性稻田土pH对反硝化最大速率常数几乎无影响，表明pH不是影响该地区稻田土壤反硝化作用的因素。

明确了反硝化动力学参数的影响因素后，本研究通过多元逐步回归分析，构建了反硝化动力学米氏方程中最大速率常数的预测模型，精度达到66%，所用到的输入项仅为土壤总氮和粉粒含量。McClellan[17]研究森林土壤反硝化作用发现，利用土壤NO– 3-N、总氮和pH能解释反硝化氮损失的61%，这表明利用土壤基本性质可以较好地预测土壤反硝化作用，同时也表明对于不同土地利用方式，土壤反硝化作用估算所选用的土壤性质有所差异，影响因素也不尽相同。

4 结论

该研究分别利用一级动力学方程和米氏方程对室内培养的亚热带典型红壤稻田土反硝化作用进行了拟合，而后用常见易得的土壤理化性质对方程中的参数进行估算。研究发现米氏方程对反硝化动力学拟合效果较好，一级动力学方程中的速率常数()和米氏方程中的最大速率常数(max)具有很强的相关性(= 0.96，<0.01)，且同时本研究得到最佳的反硝化动力学米氏常数(m)值为35 mg/kg的NO– 3-N浓度。土壤总氮，砂粒和粉粒以及土壤容重对max影响较大，最后仅利用土壤总氮和粉粒含量预测了max，得到一个较为可靠的预测模型，估算精度为66%。构建的反硝化动力学参数方程具有一定的实用性，通过利用土壤基本理化性质估算反硝化动力学参数，从而避免了获取土壤反硝化作用的繁琐培养测定，不过模型的精度还有限，表明还受其他更为复杂的因素影响，这值得进一步探讨。

[1] Zhu Z L, Chen D L. Nitrogen fertilizer use in China-contributions to food production, impacts on the environment and best management strategies[J]. Nutrient Cycling in Agroecosystems, 2002, 63(2): 117–127

[2] Kahrl F, Li Y, Su Y, et al. Greenhouse gas emissions from nitrogen fertilizer use in China[J]. Environmental Science & Policy, 2010, 13(8): 688–694

[3] Schroder J L, Zhang H, Girma K, et al. Soil acidification from long-term use of nitrogen fertilizers on winter wheat[J]. Soil Science Society of America Journal, 2011, 75(3): 957–964

[4] 曹彦圣, 付子轼, 孙会峰, 等. 施氮水平对水稻氮肥利用率和径流负荷的影响[J]. 土壤, 2016, 48(5): 868–872

[5] 熊舞, 夏永秋, 周伟, 等. 菜地氮肥用量与N2O排放的关系及硝化抑制剂效果[J]. 土壤学报, 2013, 50(4): 743– 751

[6] 王海涛, 郑天凌, 杨小茹. 土壤反硝化的分子生态学研究进展及其影响因素[J]. 农业环境科学学报, 2013, 32(10): 1915–1924

[7] 娄焕杰, 邓焕广, 王东启, 等. 上海城市河岸带土壤反硝化作用研究[J]. 环境科学学报, 2013, 33(4): 1118–1126

[8] 孙志高, 刘景双, 于君宝. 三江平原典型草甸小叶章湿地土壤的反硝化作用[J]. 农业系统科学与综合研究, 2010, 26(1): 117–122

[9] Minasny B, Hartemink A E. Predicting soil properties in the tropics[J]. Earth-Science Reviews, 2011, 106(1): 52-62

[10] Pachepsky Y A, Rawls W J, Lin H S. Hydropedology and pedotransfer functions[J]. Geoderma, 2006, 131(3): 308–316

[11] 刘光崧. 土壤理化分析与剖面描述[M]. 北京: 中国标准出版社, 1996

[12] 刘培斌, 郭亚洁. 土壤中氮素反硝化作用及其动力学规律的实验研究[J]. 华北水利水电学院学报(自然科学版), 1994, (4): 15–19

[13] Ahn C, Peralta R M. Soil properties are useful to examine denitrification function development in created mitigation wetlands[J]. Ecological Engineering, 2012, 49: 130–136

[14] 艾娜, 周建斌, 杨学云, 等. 长期施肥及撂荒土壤对不同外源氮素固持及转化的影响[J]. 中国农业科学, 2008, 41(12): 4109–4118

[15] Yu Y, Zhang J, Chen W, et al. Effect of land use on the denitrification, abundance of denitrifiers, and total nitrogen gas production in the subtropical region of China[J]. Biology and Fertility of Soils, 2014, 50(1): 105–113

[16] D’haene K, Moreels E, De Neve S, et al. Soil properties influencing the denitrification potential of Flemish agricul­tural soils[J]. Biology and Fertility of Soils, 2003, 38(6): 358–366

[17] McClellan M H. Denitrification potential in forest riparian soils of the western Oregon Cascades: Spatial and temporal variation[D]. Oregon State: Oregon State University, 1987

Estimation of Denitrification Kinetic Parameters of Paddy Soils in Subtropical China

ZOU Ganghua1, ZHAO Fengliang1, SHAN Ying1, LI Yong2*

(1 Environment and Plant Protection Institute, Chinese Academy of Tropical Agricultural Sciences, Haikou 571101, China; 2 Institute of Subtropical Agriculture, Chinese Academy of Sciences, Changsha 410125, China)

Denitrification is an important way of soil nitrogen loss, and accurate estimation of denitrification potential is the inevitable requirement of precision agricultural fertilization. The study selected subtropical paddy soils as the object. Soil samples were anaerobically incubated indoors with exogenous sufficient nitrogen (nitrate nitrogen) addition to obtain the denitrification dynamics, which were then fitted by Michaelis-Menten equation and one-order dynamic equation, respectively. Finally, basic physicochemical properties were used to estimate denitrification kinetic parameters. The results showed that Michaelis-Menten equation was more suitable for fitting the kinetics of denitrification in paddy fields. The best fitted Michaelis constant (m) was 35 mg/kg; Michaelis maximum rate constant (max) in Michaelis-Menten equation and the kinetic rate constant () in one-order dynamic equation had a significant correlation (= 0.96,<0.05). Total soil nitrogen, sand and silt content, and soil bulk density had the greatest impact onmax. Total nitrogen and silt contents were used as the inputs to estimatemax, with an accuracy of 66%. The developed function not only fully excavates the potential of soil basic data, but also can efficiently and quickly gain soil denitrification kinetic curve.

Denitrification; Enzyme kinetics; Red soil; Parametric estimation; Pedotransfer function

公益性行业(农业)科研专项(201503106)、中国热带农业科学院基本科研业务费专项资金(1630042017004)和海南省重大科技计划项目(ZDKJ2017002)资助。

(yli@isa.ac.cn)

邹刚华(1985—)，男，江西南昌人，助理研究员，主要研究方向为农业面源污染及土壤改良。E-mail：zou_ghua@163.com

S153.4

A

10.13758/j.cnki.tr.2019.03.014