基于排队论的银行服务系统优化研究

金科学 赵文静 孙洪磊

摘要：银行存在排队问题，为解决这一问题，通过实地观测，获取某支行顾客排队数据。银行的服务过程视为随机系统，建立了基于排队论M/M/c/∞/∞/FCFS的银行服务系统模型，进而求解。通过对银行服务系统排队模型的实证研究，为银行合理优化服务系统提供决策参考。

Abstract： There is a queuing problem in the bank. In order to solve this problem， the customer queuing data of a sub-branch are obtained through field observation.  The bank's service process is regarded as a stochastic system， and a model of bank service system based on queuing theory M/M/C/∞/∞/FCFS is established and then solved. Through the empirical study on the queuing model of the banking service system， it provides a reference for banks to optimize the service system reasonably.

關键词：排队论;极大似然估计;泊松分布

Key words： queuing theory;maximum likelihood estimation;Poisson distribution

中图分类号：O226;F832.3                             文献标识码：A                                  文章编号：1006-4311（2019）18-0071-04

0  引言

在社会经济高速发展的情况下，在资源有限的情况下出现了大量的排队现象，银行排队现象尤其严重。随着生活质量的提高，银行的业务范围也随之更加广泛，如信用卡贷款、网上银行开通、金融理财等各种业务。我国五大银行也做出相应的声明，即用户通过手机银行进行的个人业务不再收取费用，这无疑方便了人民的生活，缩短了银行排队时间，提高了效率。尽管如此，银行排队问题依然显著存在。目前，银行存在排队问题，增加设备投入和柜台可以降低顾客的等待成本，减少顾客的损失，但同时会增加银行经营成本，在缓解顾客排队问题的同时又产生了新问题。因此如何提高银行的效率和顾客满意度，缩短银行顾客排队的时间，降低银行运营成本是一个很重要的问题。

本文选取的银行临近学校及住宅，学校的学生经济来源一般是父母转账来实现的，学校的很多业务与银行往来，如学费代扣、奖学金助学金的发放、科研项目相关费用、教职工工资、学生生源地贷款等等。因此该银行是周围学校和居民使用需求非常高的一个场所，其个人业务窗口顾客排队情况严重。

本文结构如下：第一部分介绍了银行服务现状及选取试点银行的依据;第二部分对该银行网点的顾客进行了满意度调查，发现顾客对银行排队时间和银行服务窗口数量设置少的满意度较低;第三部分建立银行排队模型，包括相关指标的获取、模型的优化对比、服务窗口数量的确定;第四部分针对以上问题提出了具体的解决措施;第五部分，全文总结。

1  银行网点顾客满意度现状调查及分析

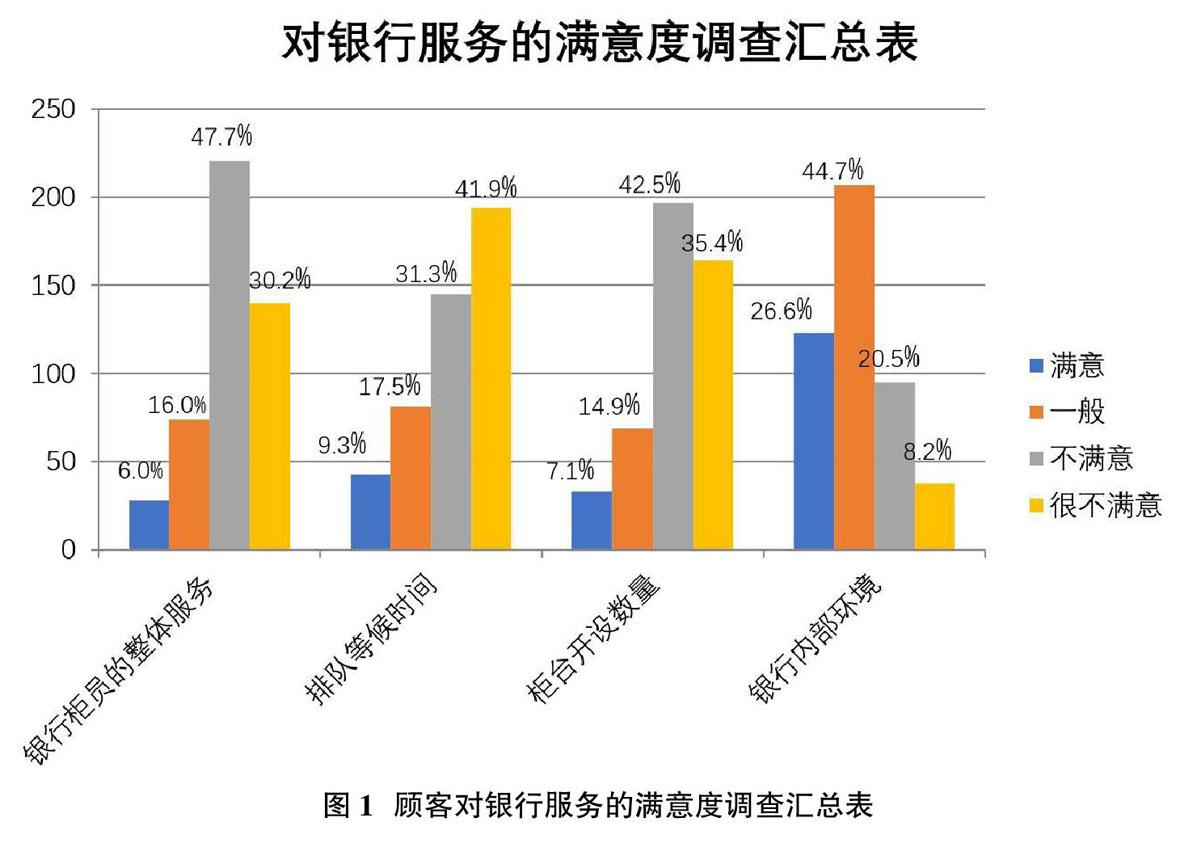
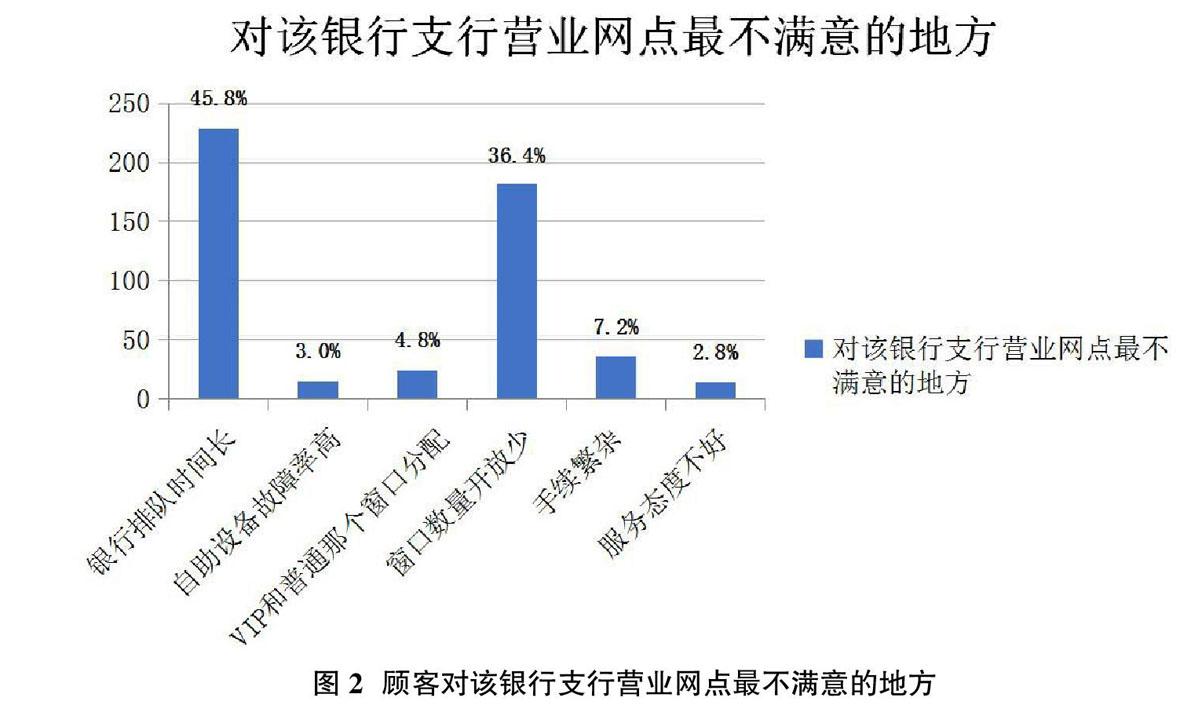
随着生活节奏的加快，居民的时间观念也越来越被重视，其去银行办理业务，怎样缩短排队时间是其最关心的问题。顾客在银行排队时间长，会使其耐心下降，对银行的体验感越来越差，抱怨增多。通过自身多次去银行办理业务的体验以及采访周围人对银行排队的感受，制作了一个问卷，调查对象是去银行办理业务的用户、周围学校学生、居民等;调查方式为线上线下相结合的方式;本次问卷调查实发数量为500份，收回问卷482份，有效问卷为463份。通过对问卷结果的分析，可以发现该银行网点存在的问题。经过对463份有效问卷进行整理，汇总如图1所示;开放性问题汇总如图2所示。

由图1、图2可得，有超过47.7%的对银行柜员的整体服务不满意，超过73.2%的顾客对银行排队时间不满意，超过77.7%的顾客对银行开设的柜台数量不满意，大部分人对银行环境表示认可。通过开放性问题的调查，顾客对银行网点最不满意的地方排名前两位为银行排队时间长和窗口开放数量少，这两个比例之和竟高达82.2%。对这两个问题的反馈远远超过了其它问题，因此怎样合理设置窗口数量，缩短排队时间，提高银行效率是一个亟待解决的问题。

2  该银行网点排队模型的优化

2.1 银行排队模型的分析及假设

顾客取号分为个人业务和VIP业务。目前该支行采用单队列多服务台，叫号机叫号的方式，严格执行了“先到先服务”的原则，且该支行内部有3个柜台。本研究将研究对象锁定为顾客到达时间间隔、服务时间、排队等待时间下的窗口开放数的研究。

本文所要研究的是单队列多服务台排队系统。当顾客到达时，若没有服务台空闲，则进入队列;当有一个服务台空闲时，排在队列中的一个顾客即进入此服务台接受服务，服务结束后离开系统。

为了简化该服务系统模型，首先对该系统进行合理的假设：①顾客进入系统后接受服务的顺序是公平的，即先到者优先接收服务。②各服务台业务员的业务速度是一致的。这是一种理想的，简化的情况。

2.2 相关参数的获取

2.2.1 顾客平均到达率的确定

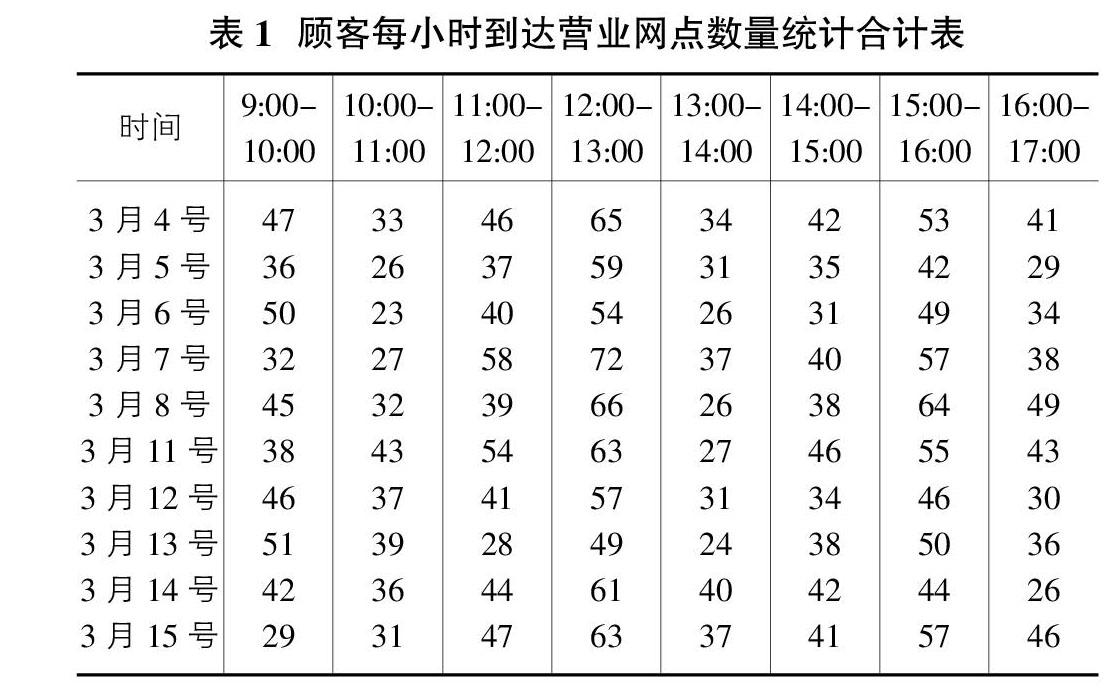
对于顾客平均到达率的确定，本文采用实地调查法确定，通过在银行网点进行两个周的实地调研，调研日期区分工作日和非工作日，本文为了更加真实的记录数据，选择了工作日进行调研，记录每个工作日内在每个时间段的人流量，进而计算出顾客平均到达率？姿，统计数据如表1所示。

假设顾客平均达到率入服从泊松分布，根据极大似然估计法，可以利用表中数据，求得泊松分布的参数λ，即旅客的平均到达率为：

2.2.2 银行服务系统平均服务率μ的确定

本文采用实地观测法确定银行服务系统平均服务率μ。随机调查了去该银行网点办理银行业务的26位顾客，由于一个顾客可能办理多个业务，故统计按照业务量和耗时进行。整理如表2。

由表2可得，平均服务速率最短的为1.6分钟，最长的为15分钟，大部分在2-6分钟内完成。假设银行服务系统平均服务率服从负指数分布，通过对表2中的数据进行数理统计分析，运用运筹学相关知识对银行柜台服务人员的平均服务率进行估算。

银行服务系统的平均服务时间=

银行服务系统的平均服务率μ=0.223人/min。

2.3 银行排队系统模型的建立及特征指标

在银行排队系统中，顾客来源是无限的，这是一个无限源系统。银行采用排队随机系统，进入系統的顾客拿号排队，依次接受服务，一般情况下银行大厅较等待的顾客来说空间比较充裕，不需要限定系统的最大客户数，即系统能够容纳的顾客人数是无限的。银行服务窗口之间是相互独立的，且其概率服从参数为的负指数分布。在该M/M/c系统中，顾客的到达时间间隔服从参数为λ的泊松分布，则两次到达之间的时间间隔为1/λ;每个旅客的服务时间是相互独立且服从参数为μ的负指数分布，则平均服务时间为1/μ。即该服务系统是一个输入为泊松分布、服务为负指数分布、c个开放的售票窗口，顾客源为无限、系统容量不受限制的等待制排队模型。

本文主要研究的是排队中的稳定性能指标，当系统经过长时间的运行之后，系统各项性能指标不再变化，处于稳定状态。当银行排队系统中的平均到达率λ和平均服务率μ到达稳定时，系统的服务强度ρ=λ/cμ，当得到系统中顾客到达的数据和接受服务的数据之后，得到系统的特征指标如下：

在进行求解时，除了计算c=3时的解，还要计算c=4，c=5，c=6时模型解，进行对比，以此进行优化，从而找出该支行排队问题的解决策略。优化本文的模型时，主要考虑两个方面：Lq对服务窗口的灵敏度和服务窗口的服务强度。

①Lq对服务窗口的灵敏度σ。它主要反映服务窗口对队长的敏感程度，当服务窗口发生变化时，灵敏度也会变化，此时选择灵敏度最大的窗口。在计算优化时，当有两个及以上窗口的最大灵敏度相近时，应该选择两个窗口间灵敏度变化幅度最大的那个窗口数。

②服务窗口的服务程度。本文系统的排队强度应为ρ=λ/cμ。当ρ>1时，单位时间内进入系统的顾客数大于单位时间内系统服务窗口所能接受的顾客数，服务窗口前的排队人数会越来越长，系统将不稳定，这是极不合理的。在ρ=1时，单位时间按内进入系统的顾客正好能够在这段时间内全部接受服务，此时所有的服务窗口全部处于忙碌状态，没有休息时间，这也是不合理的。因此，当ρ<1时，服务强度是最合理的。

2.5 银行排队服务系统模型的优化对比

分别计算c=3，4，5，6时各项性能指标的变化，从而计算？滋和？滓，然后进行对比。计算结果如表3和表4。

由表3可知，表中所有服务窗口数的服务强度均满足要求，此时需对σ进行对比。由表4得知，在未计算出c=3的敏感度时，c=4时的敏感度最大，对敏感度小的窗口不考虑。在三个窗口和四个窗口的ρ和σ都符合要求下，我们从以下几个方面考虑：

①ρ之前已经分析过ρ>1和ρ=1时不合理的，而ρ<1符合要求。此时认为，ρ的值越小，服务窗口越空闲，服务人员会有充足的时间来进行一定量的休息。c=3时，ρ=0.9347，比较接近于所有的服务窗口全部处于忙碌状态的情况。而c=4时，ρ=0.7007，此时相对于c=3的情况，ρ的值距离1较远，此时，服务人员会有一定量的休息时间，符合现实情况。

②Lq，Ls，Wq，Ws。现实中，为了解决银行排队现象，银行希望在一定的时间段内排队的顾客数和系统中的平均顾客数相对少一点，这样有利于银行内的人流及时疏散。而顾客则希望自己的等待时间和逗留时间短一些，这样也会减少顾客的不满情绪。对比c=3和c=4两种情况，发现c=4时符合实际情况。

3  银行排队服务系统的解决方案

本文通过建立银行排队服务系统，分析了ρ与1的关系，σ的大小，以及Lq，Ls，Wq，Ws的实际情况的对比，得出以下结论：在该银行支行营业网点，4个窗口的情况会更加符合实际，并且会减少顾客的排队时间，提高顾客的满意度，同时提高银行间的竞争力，为现代银行的经营管理提供决策参考。

除了设置更为合理的窗口数量，从服务效率角度来看，可以通过以下几个方面提高服务效率：①提高银行系统人员的服务效率。②优化银行业务流程。③采用顾客分流的渠道措施。④改变顾客排队方式。从银行窗口设置和现场改善的角度考虑，可以通过以下几方面来提高银行的服务质量：①服务窗口数量和服务时间设置为弹性的。在高峰时间段的日期，增加窗口数量和服务人员，服务人员采用倒班。②改善现场环境。在等待的时间里，通过现场宣讲的有关金融知识的视频或者有关活动来降低顾客的不满情绪。③加强排队秩序和现场营业大厅管理。

4  结语

在生活节奏越来越快的现代社会，怎么节省时间尤为重要，银行又是与人们生活息息相关的场所，银行排队等待问题的缓解成为了大家关注的焦点。本文通过对银行网点进行的满意度调查及分析，发现顾客对银行排队问题和服务窗口数量设置不合适的满意度非常低，进而建立了银行排队系统的模型，并进行了优化对比分析，最后得出该银行网点设置4个服务窗口数量最为合适，并从其他角度提出了银行服务效率的措施，以期对银行服务效率有所改善。

参考文献：

[1]《运筹学》教材编写组编.运筹学[M].三版.北京：清华大学出版社，2005，6：324-325.

[2]李海琳.运用排队论模型测量医院门诊流程效率[J].中国管理信息化，2015（6）：97.

[3]杨米沙.银行排队系统数据分析及窗口设置优化研究[J].武汉理工大学学报，2008，08.

[4]范文宇，苑辉.基于排队论的银行客户服务系统问题研究[J].价值工程，2005（12）.

[5]陆建.最小二乘法及其应用[J].中西部科技，2007（12）.

[6]徐力，宁洪.迭代法求解非线性方程组（蔟）应用优化[J].电脑信息与技术，2000（1）.

[7]高珊，崔艳.基于不耐烦顾客和可变服务率的可修M/M/1/N-G排队系统[J].黑龙江大学自然科学学报，2015，12：743-752.

[8]张晓磊，马从安，申晨.基于排队论的车站售票系统优化与改善[J].工业工程与管理.

[9]李娜，贾博，江志斌，等.考虑顾客体验的排队系统研究[J].工业工程与管理，2012，17（3）：36-40，46.

[10]石芳玉.基于排队论的银行网点顾客排队优化管理研究——以A银行CDUT支行为例[D].成都理工大学，2016.

[11]宋卫斌，苏秦.虚拟客户服务系统排队模型[J].管理科学学报，2001，4（3）：52-57.