由同心圆到等时圈——山地城市教育设施动态模拟评价探索

吴朝宇，周翔

（重庆市规划信息服务中心，重庆 400020）

吴朝宇，周翔.由同心圆到等时圈——山地城市教育设施动态模拟评价探索[J].重庆建筑，2019（7）：5-9.

0 引言

重庆是典型的山地城市，由于山地特殊的地形、地貌条件决定了其在空间上的隔绝性、生态环境上的多样性以及可建设用地的相对稀缺性。因此，为探索实现山地城市公共服务设施的最优化配置，需要结合山地地形实际特点和空间的可达性，在传统的同心圆模型均衡配置的基础上进一步优化，建立能够体现山地特征和需求差异的公共设施服务能力模型。

本文在重庆市规划和自然资源局已有的空间大数据平台支撑下，结合传统的中小学布点规划编制存在的不足，通过大数据分析模型的建立，以人的可达性为研究方向，分析评价教育设施的供给与需求，并提出建设时序建议。为教育设施在规划布局和建设时序上面临的实际问题提供决策依据，也对提高政府投放城市公共产品的精准性、公共服务的高效性进行研究。

1 教育设施布点规划的不足及思考

一般情况下教育设施布点规划编制通常以国家居住区或者中小学建筑设计规范，或本市颁布的地方标准为依据。规划标准按照中小学、幼儿园等教育设施阶段规定的服务半径及千人指标，以中小学规划布点为中心，划定其服务周边居住用地的同心圆来测算中小学能否实现半径覆盖[1]（图1）。在规划实施阶段，根据教育主管部门反馈意见，按同心圆模式进行布点存在三个方面的问题。首先，因用地紧张等限制性条件，以服务半径划分服务区造成了服务区重叠或无法全覆盖，从而造成空间分布的失衡；其次，布点规划为规划期内用地与相关设施统筹布局的最终状态型规划，而在年度具体实施中，结合用地态势，对规划设施的建设时序的动态引导方面就显得较为薄弱；三是同心圆布局模式采用空间直线距离来度量，而重庆作为山地城市，受地形高差影响，空间直线距离不等同于实际入学步行时间，使规划预期与实际情况出现一定的差异性。

近年来，国内很多城市运用GIS地理信息系统对公共服务设施空间服务能力的探索日益普遍，其主要方式是采用改进泰森多边形（Thiessen Polygons）进行计算，按照生源至小学空间距离最短原则划定服务边界并建立缓冲区模型[2]（图2），这种方式相比同心圆方式单纯依靠服务半径具有很大的改进，但计算结果依然反映的是空间上的直线距离。

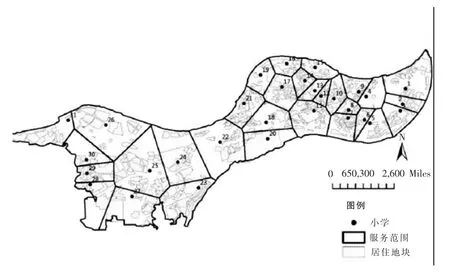
图2 泰森多边形模拟教育设施服务半径示例

综上所述，同心圆模式按照相关规范要求划定公共服务设施服务半径的方式，能够实现在区域层面对公共服务设施覆盖能力进行整体性评估，但无法对半径重叠和覆盖不足进行更深入的分析；改进泰森多边形优化了同心圆，形成边界不相重叠的服务范围，能够更为精确地模拟教育设施服务半径，但基于空间直线距离建立的缓冲区模型无法准确量化反映因地形高差变化对实际可达时间的影响[3]。因此，本次研究拟在改进泰森多边形基础上，建立以人的步行时间为量度来评价公共服务设施服务半径的等时圈模型，从而更加精确地评估和量化山地城市公共服务设施实际服务能力和空间匹配度。

2 研究内容与技术方法

2.1 研究对象及主要内容

重庆市采取的为多中心组团式结构布局，主城区共划分为21个城市组团，一个组团内形成完整的产业、居住及相关公共配套服务，并承担具体的城市功能。本次研究选取重庆市南岸区茶园组团，茶园组团位于主城东南部，因南山和长江的天然分隔，其组团功能相对独立，能够减少因跨组团入学产生的数据干扰情况。组团现状常住人口共32万人，学生约1.4万人，现状已建成小学共10所；规划城市建设用地约65平方公里，规划规划人口共约70万人，学生约3.5万人，规划小学共38所，小学容量4.7万人（图3）。

图3 重庆江南新城区位及土地利用规划图

本次研究基于区域现状和法定控规及专项规划，在小学布局和服务能力既定的情况下，以各学校的等时圈为基础，建立需求-供给-供需匹配三个层次的数据关系模型，通过模型来模拟评估现状及规划中小学服务能力。同时，在评估结果的基础上，依托规划信息化平台，将准现状（动态规划许可）纳入评估模型系统，更进一步计算因准现状至现状建成而即将产生的新增入学需求，以及在此需求下为中小学最优化选址建设实施提供建议。

2.2 研究方法及技术路线

研究使用地理信息系统软件Arcgis进行模拟计算，基础数据结合重庆市规划和自然资源局信息中心建立的城乡规划综合数据平台，并结合高德地图POI网络数据进行。在对搜集的各项数据进行整理后，建立数学模型。

2.2.1 运用的模型技术

本次研究主要利用三种数学模型来进行计算：（1）指数平滑法1，主要是用于推导居住用地规划许可选址阶段到建成所需要的平均建设时间。指数平滑法是基于时间序列推导人口及建设发展情况常用模型，在跟踪及预测五年之内的变化趋势较为与实际情况拟合。（2）层次分析法2，主要用于对居住用地建成后周边各项配套设施成熟度的研究，从而判定地块实际入住人口和入学需求。层次分析法作为经典的决策分析方法，利用较少的定量信息使决策的思维过程数学化，从而为多目标、多准则或无结构性的复杂决策问题提供简便的决策方法。通过层次分析法结合GIS来分析公共设施的选址或布局是当前较为可行的实现方法[5]。（3）模拟退火算法3，本次核心模型，即通过设定目标条件，计算机通过循环计算寻找最优化结果的计算方法，用于人口增加后判定最优化学校建设时序的建议（图4）。模拟退火方法源于固体退火原理的迭代计算，首先程序开始于一个很高的温度，此时好的、坏的解都可能被接受；当温度不断降低后，坏的解被接受的概率越来越小，最终只有好的解才被接受。模拟退火算法并不能保证找到最优解，其计算结构只是近似最优的。然而在实际中，这样的近似解已经足够了，因为计算结果不可能考虑得面面俱到，而只是提供一种参考方案，并让决策者能够较为清晰直观地进行决策。

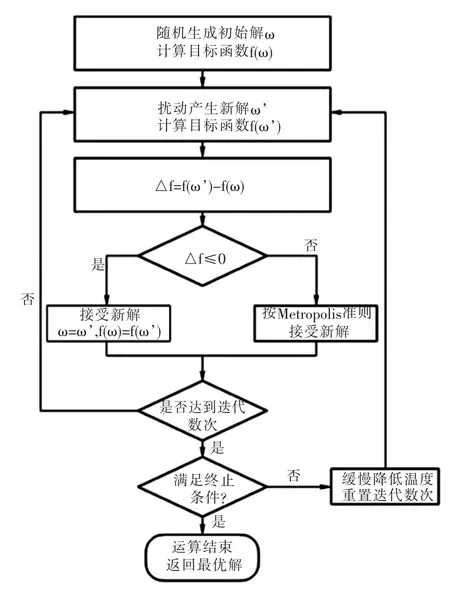
图4 模拟退火算法求解模型

2.2.2 工作技术路线

在技术路线上建立现状、规划期末、规划实施过程动态演进的用地实施时间轴，即模拟评估现状供需、区域规划供需总量、动态评估规划实施供需三个方面开展。具体工作流程为：（1）现状人口数据空间离散，确定现状需求及空间分布；（2）现状小学空间匹配，以实际出行时间建立小学等时圈；（3）规划数据匹配，计算规划用地人口及中小学需求；（4）数据关联计算及图表分析，进行现状评估及规划评估；（5）动态许可数据载入，实时计算近期供需情况及最优化小学建设时序。

3 基于现状及控规的小学配套能力评估

3.1 现状服务能力评价

3.1.1 人口统计数据的空间离散

户政管理部门的常住人口统计数据精确到街道和社区层面，而规划建设部门能够较为精确地掌握现状建成信息。为实现常住人口与城市现状建成情况结合，需要把常住人口数据与地块建成情况进行匹配，实现人口数据的空间矢量化，并作为计算居住用地入学需求量的基础。在空间矢量化过程中，通过手机信令数据对人口的空间分布进一步进行了校正和核对，使人口统计数据较为准确地离散至控规地块。

3.1.2 典型学校“等时圈”模型的搭建

利用高德地图提供的WebAPI，将学校和居住用地的空间数据导入高德地图开放接口，模拟步行经过的通道和距离，计算学校规划点到各个居住地块步行距离和时间，然后将数据矢量化。之后，利用GIS的3D分析模块，将目标点图层转化为Tin类型，将栅格转为矢量图层和中小学等时圈的面图层，最后在ArcMap中，采用分级颜色图对结果进行渲染，得到该学校的等时圈图（图5）。

从等时圈图可以看出，1000m范围主要位于20～25min等时圈范围，超过规范中1000m所对应的15min入学距离较多。可见，以等时圈评估学校服务范围，较规范中的1000m同心圆更为精确，对重庆市地形高差更大的区域，其对比结果将更加明显。

3.1.3 对现状教育服务能力的整体评价

对每个现状学校和用地划定等时圈后，运用“模拟退火”的算法，确定学校与居住用地的匹配关系，并如实反应历史因素造成的远距离入学。通过对计算成果进行渲染和可视化展示，可以计算出江南新城现状总小学生人数1.38万人，10所小学总容量1.35万人，基本上满足适龄儿童均入学要求，但位于中心区的四所优质学校均为大班额的超饱和状态；在学校与居住地块空间匹配关系上，上学时间超过15min的居住地块数量达到300余个，涉及学生人数0.82万人，平均上学时间为19min（图6）。

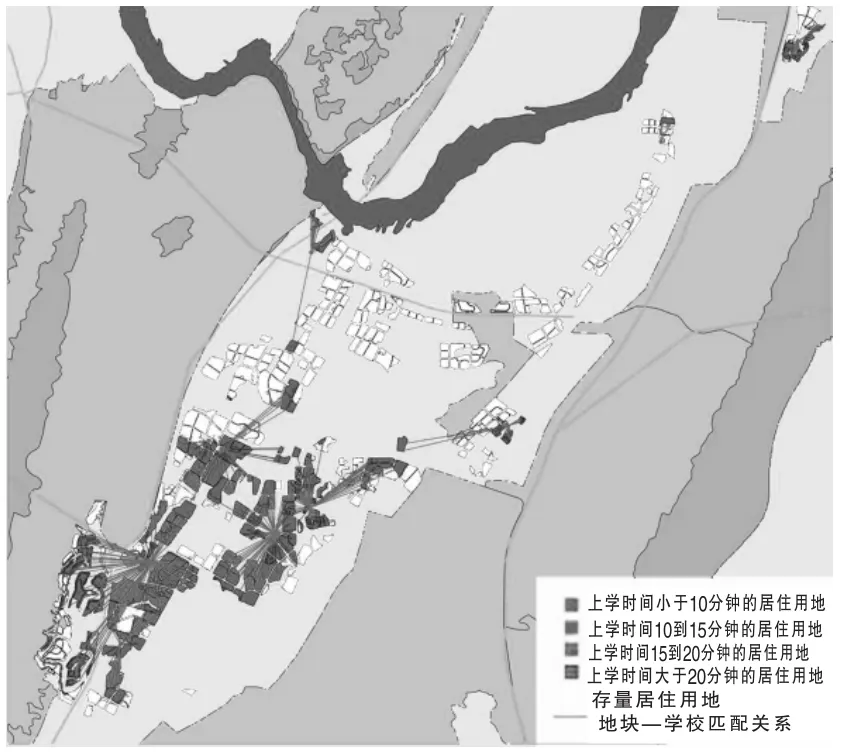
图6 现状教育设施服务能力评价图

由此可见，通过大数据结合的等时圈模式来评价教育设施服务能力比传统的同心圆模式能够更加精准地体现教育设施配套能力，以人为本地反映“上学难”存在的实际问题。

3.2 规划服务能力评价

在现状评估的基础上，对未实施的居住和中小学用地，载入区域内控制性详细规划的居住用地和学校的控制指标。其中，对于未建设的存量居住用地结合重庆市人均居住面积、地块容积率和居住品质计算规划人口；规划学校按照专项规划确定的学位数计算。

按照教育资源的逐步实现均衡化要求，规划学校的增加会逐步消减现状存在的不平衡状态，因此，必须采用“模拟退火”的算法，重新确定学校与居住用地的匹配关系。按照规划情况计算服务能力，计算并表达规划期末的各规划学校的服务饱和度情况，以及各居住用地的入学难度（图7）。

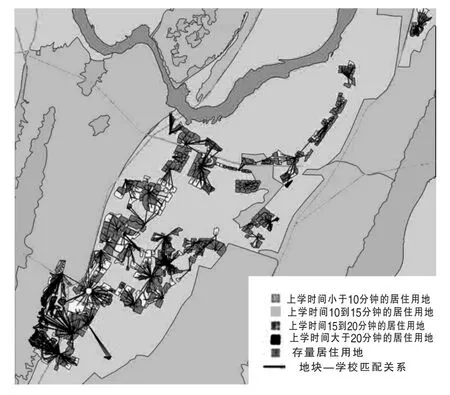
图7 规划教育设施服务能力评价图

按照规划总量计算，区域内学生人数3.5万人，小学容量4.6万人，其总量规模完全能够满足区域人口入学需求。上学不便的人数为0.4万人，大大低于现状分析情况，其地块分布主要集中在西南角的高端居住区域。在学校饱和度方面，38所学校中有8所学校仍然存在超饱和状态，但相对于现状情况已大有缓和，说明布点规划较好地满足了区域教育设施整体性配套的要求。通过规划模型系统的建立，可以对教育设施布点规划编制提供客观的评价和校核工具，提高布点规划编制的科学合理性。

4 基于建设动态的小学配套能力评估

通过以上数据模型的搭建，能够实现在特定时间点对小学的现状及规划情况进行系统化的评估。但城市是不断发展的，为使评估系统能够动态跟踪城市建设行为和人口增长情况，使其保持持久的生命力和即时的决策支持能力，就有必要将与中小学有关的建设实施情况动态纳入系统，由计算机智能计算来实现提前预警式评估和最优化小学建设选址分析。

4.1 规划用地实施的动态引入

依托重庆市城乡规划综合数据库十余年的建设，从2005年起在重庆主城区实现了规划许可在线办理和实时动态入库功能。因此，本次研究将教育设施配套能力评估与规划用地实施进行动态挂接，在建设用地发放用地条件函至竣工验收的规划许可周期（特别是居住用地）来计算建成及入住的时间周期（表1），用以计算未来即将新增的学位需求和需同步新增小学建设的临界值，从而实现人口的实际增长和公共服务设施的同步配套建设双同步。

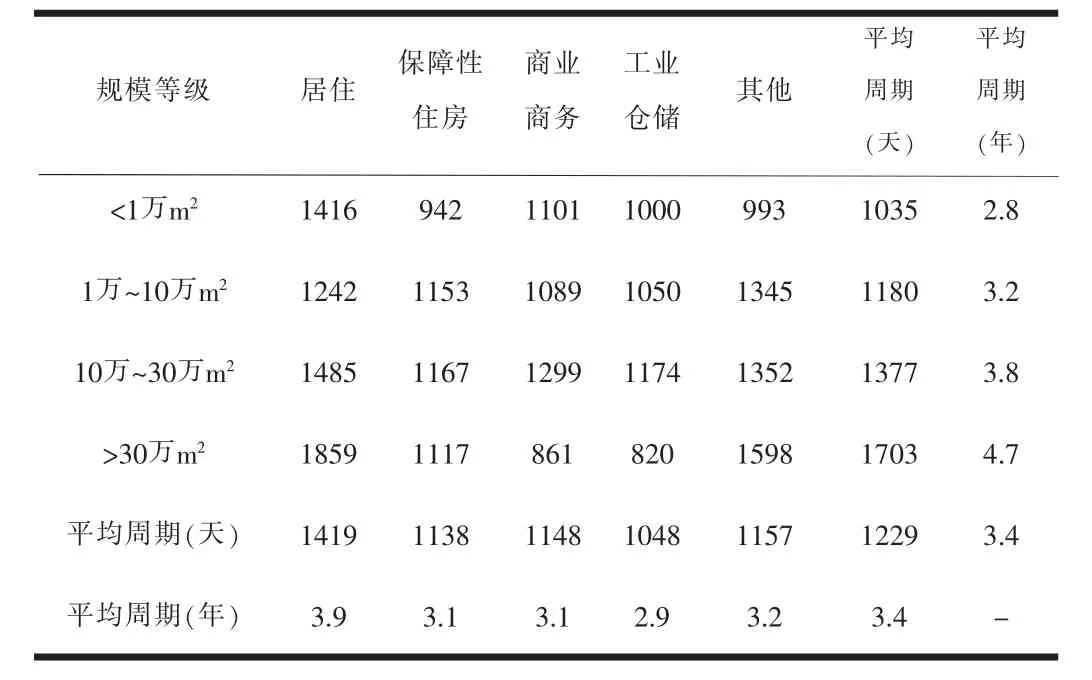
表1 主城区建设项目实施周期分析

研究对主城区近10年来各类型项目平均实施周期进行统计，计算出江南新城在2018年前进入规划审批的居住用地，将在2020年前完成项目竣工规划核实，这部分“已批、在建建筑”将在2020年成为“现状建筑”（图8）。

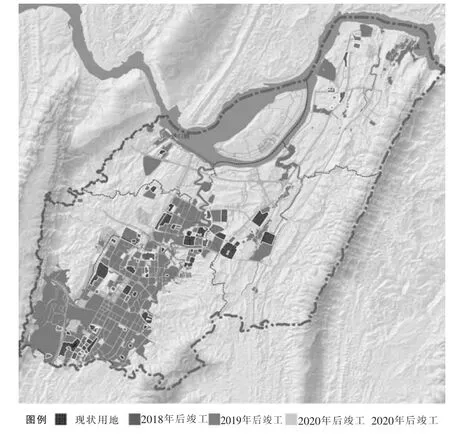
图8 江南新城在建项目态势图

4.2 用地实施后的入学需求预测

实际入学需求需要在实际人口入住后才能产生，因此，对居住地块入住率的预测为后续的重点。而实际入住人口主要受用地的住宅类型和居住地块周边成熟度两个因素影响。其中，住宅类型决定入住率基数，本次研究在近十年同类型的入住率统计基础上，采用一次指数平滑法，推算得出2020年相同类型用地的入住率基数。另一方面，地块成熟度决定入住率系数，本次研究选取“公交、轨道、公园绿地、POI、路网”5个因子，用层次分析法由专家按照重庆实际情况，对各因子进行两两比对评价，得出评价矩阵，带入计算得出各因子相对权重（图9）。对各个居住地块的不同情况按照权重打分，计算入住率系数。通过这种方式，建立：入住率-人口数-学位需求数，从而建立入学学位需求预测模型，其模型公式为：p=S/rx{f+[(l-f)x∑wixSi]/100}x0.048。

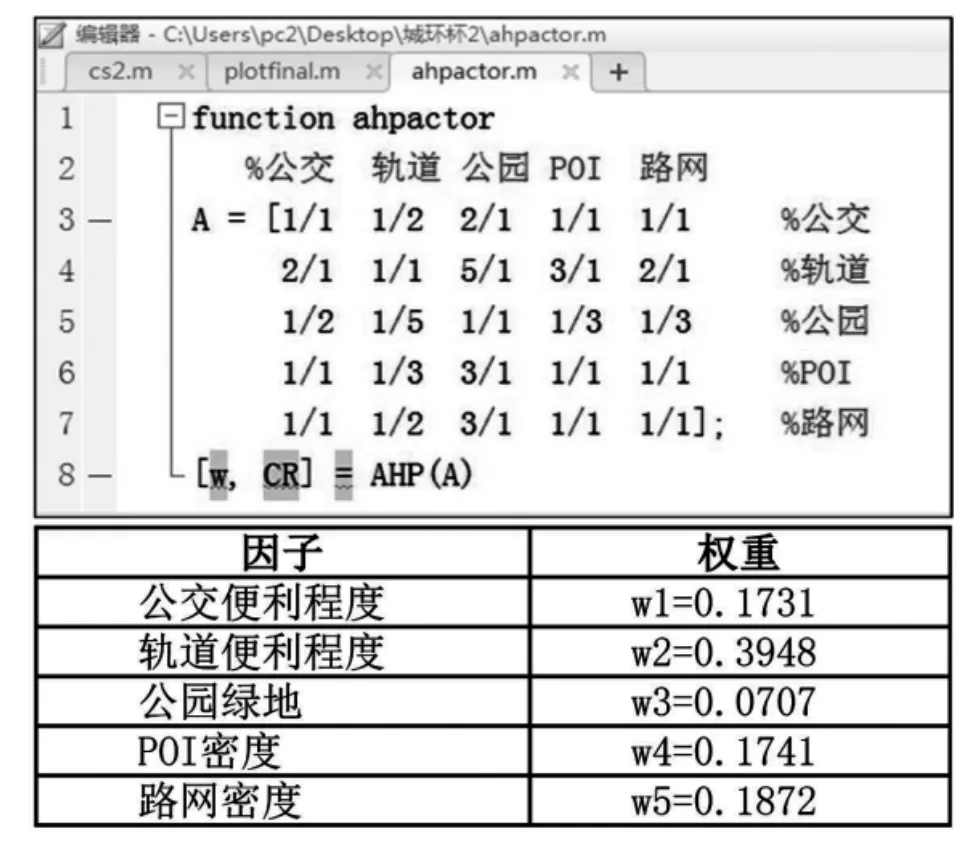
图9 利用层次分析法计算入住率系数

4.3 新增需求的小学用地分配及选址判定

通过用地实施后入学需求预测，在2020年区域实际居住人口将从当前的32万人增加至45万人，学生数量从约1.4万人增加至约1.65万人，需新增两所小学解决现状缺口及满足近期新增实际居住人口入学需求。

在以人口为中心计算中小学需求后，以控规中布局的中小学为对象，计算中小学能够提供的实际供给能力。分配模型以所有学生的平均上学时间、上学不便的学生数量、入学不便的地块数量作为评价标准，来实现区域内所有学生上学总时间最少，超员接受学生的学校数量最少，各学校利用效率最大化的目标。求解方式运用MATLAB软件，采用“模拟退火”的算法，分配合理的“居住地块-学校”匹配关系，求解出新建学校的最佳位置。

通过计算机模拟计算，在图10中新建点1、点2两所规划小学，能够最大化满足中心区域多数地块上学需求，平均上学时间缩减至13 min左右。同时，现状超饱和状态的点3、点4两所小学的饱和度也得到了极大的改善。同时，在江南新城西南角区域出现学校学位总量满足要求的情况下依然有上学距离超出规范的情况，经分析该区域为高档别墅区，城市快速路的阻隔导致步行交通不便。因此，本次规划研究的结论中建议在该区域新增步行通道解决入学距离问题（图10）。

图10 在建居住项目新增学位需求分配图

5 结语

本次以小学为例，在区域现状和规划情况确定的情景下研究公共服务设施服务半径、服务能力和空间匹配度。针对传统的按照设计规范的“同心圆”方式划分服务半径的局限性，以GIS网络分析为基础，基于人口空间分布和山地地形的出行特征，确定各学校步行可达的“等时圈”，通过等时圈的建立，评估分析公共服务设施选址布局存在的问题及改进方向。研究进一步依托实施管理动态数据的载入，将评估系统由静态评估向一定程度上的动态学习和智能预警方向创新拓展。

经验证，模型较为真实地模拟了小学供需的空间关系和生源的出行方式。但由于人口数据采取的人工空间离散，生源和学校之间采取的唯一性匹配方式等因素，使模拟的结果与实际运行情况无法达到完全的一致性。在这方面，技术上不存在障碍，随着数据信息的进一步积累和集成，可以逐步完善和调整模型相关参数来优化匹配。

将研究的结论与所涉及的区政府和教育主管部门进行了交流，可知其准确地反映了江南新城教育设施未来发展需求，提出的教育设施和交通改善建议被纳入当年城市提升行动计划实施项目。希望该评价方式的建立能够对大数据时代更为精细地编制公共服务设施类规划提供拓展思路。

注：

1指数平滑法：是一种特殊的加权移动平均法。即由过往数据推算未来数据的一种加权算法。算法认为时间序列的态势具有相对稳定性，所以时间序列可被合理地向未来推演；并且，对过往的统计数据赋予不同权重，较近期数据的权数大于远期数据。一次指数平滑预测公式：yt+1’=ayt+(1-a)yt’。

2层次分析法：（Analytic Hierarchy Process），一种层次权重决策分析方法。对一些较为复杂、模糊的问题，特别是难于完全定量分析的问题，提出的一种简洁而实用的建模方法。

3模拟退火算法 （Simulate Anneal，SA），一种通用概率演算法，用于在较大范围内找寻命题的最优解。