离心泵H-Q出厂性能曲线拟合与校正

成庆林，马妍欣，杨金威，冯 云，甘亦凡，黄作男

（东北石油大学提高油气采收率教育部重点实验室，黑龙江大庆163318）

在工程建设中，为确定离心泵的开泵方案，一般需要知道离心泵的特性曲线方程。离心泵的特性曲线或有关设计材料都是以参数或图形的形式给出的，并没有明确的表达式，难以得到具体的泵性能参数。如何选择合适的数学拟合模型，数学拟合模型参数的确定及将离心泵的性能曲线转换为计算机语言下的图形是拟合的关键问题[1]。为此，对离心泵的H-Q曲线进行幂函数、多项式以及指数拟合，并对其进行误差分析，选出最优拟合方程[2]。

由于设备厂家提供的泵性能曲线H-Q与实际运行存在一定偏差，造成模拟计算结果与实际不符，影响运行方案的制定，因此要对拟合后的离心泵H-Q性能曲线进行校正。

1 曲线拟合基本原理——最小二乘法

在实际工程中，大部分通过人为观测的数据都有误差，此时若要求一条曲线经过所有已知点是不合理的。因此为解决离心泵性能曲线拟合问题，尽可能全面地反映实际数据的变化规律，必然要求每个离散点上的计算值与实际值的绝对值之差尽可能小，通常要求误差平方和最小即可。拟合过程中采集的实际数据越多，则拟合效果越好，函数曲线越精确[3]。

若假设变量为X1,X2,…,Xn,y1,y2,…,yt(t≥n)，通过下面的算式计算得到：

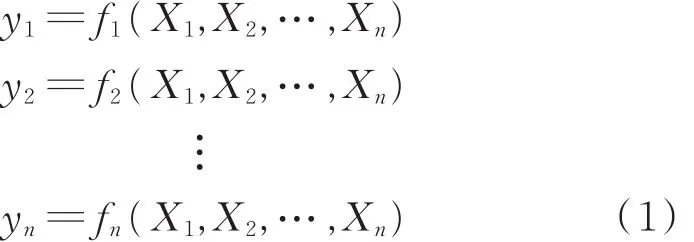
假如Xa为真实值，利用上述公式可求出真实的ya，假如测量值为y*a，则计算的误差为：

则最小二乘法可表示为：

若进行测量的精度不等，则应在上述的计算基础上加上各个测量值的权重因子Pa，则式（3）改写为：

研究的最小二乘法是建立在随机误差呈现正态分布时，利用最大似然理论所推导出的结果。

2 离心泵H-Q曲线幂函数拟合

采用VB语言对H-Q曲线进行幂函数形式的拟合。

（1）拟合方程式建立

对于固定转速下的离心泵，可通过实测不少于5组的H-Q数据来对其性能曲线进行最小二乘法拟合，得到如下的函数表达式：

式中，Q为离心泵流量，m3/h；H为离心泵扬程，m;a、b为待定系数，由实测或泵特性曲线上得到的n组（Q，H）数据根据最小二乘法回归得到；m为流态指数，层流m=1，水力光滑区m=0.250，混合摩擦区m=0.123，粗糙区 m=0。

（2）待定系数确定

根据最小二乘法定义，最小二乘法如式（6）所示：

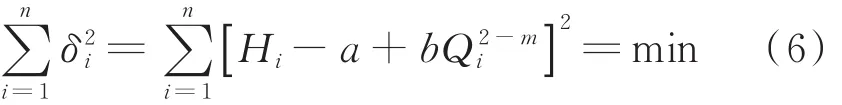
假如式（2）成立，则式（7）成立：

求解式（3）得：

式中，n为泵样本所测试的Q、H数据组数。

（3）编程

①打开VB6.0，创建一个标准工程文件[4]。按设计要求对新建的工程文件进行可视化设计（见图1），主要满足7个功能：查看数据、曲线拟合公式、拟合图像、清除、误差分析、保存以及帮助。窗口设计3个Text文本框和一个PictureBox。3个文本框分别用来表示输出拟合点数据、输出拟合公式、输出误差值。

②在设计完窗口后，需要根据事先选定好的数学模型进行编程求解。代码应尽量不繁琐，简单易懂。尽量少地调用程序块，以增加程序的运行速度。编程思路如下：

A.在VB6.0的代码窗口中对所需要使用的各个变量进行定义。

B.将数据进行筛选，利用最小二乘法写出对应方程组。

C.对方程组进行求解并将其结果输出到窗口中。

③编程结束后，应对工程进行不断调试，若发现问题应及时调整，直到符合要求。

（4）求解并检验拟合误差

为了计算拟合误差，采用如下方程式计算误差。

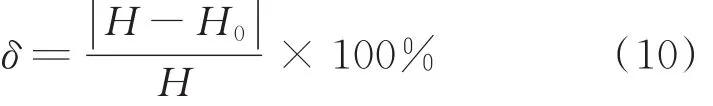
式中，H为样本值或实测值，m；H0为拟合方程的计算值，m。

为了验证幂函数拟合的H-Q性能曲线方程的可行性，若拟合后精确度大于等于95%，则认为拟合效果良好。

3 离心泵H-Q曲线多项式拟合

用VB语言编程对其实现多项式拟合[5-7]。

（1）拟合方程式建立

设拟合多项式的次数为m,则需拟合的方程形式可表示为：

式中，Xj为待定系数，j=0,1,⋅⋅⋅，m。

将方程改写为：

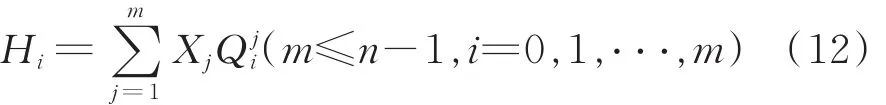
（2）待定系数确定

将式（12）改写成如下矩阵形式[8⁃10]：

根据最小二乘法定义对式（13）进行求解，则式（13）应满足如下关系式：

解方程求得X=(A'A)-1(A'B)。

由Runge现象可知，多项式拟合次数越高，拟合精度未必越高。为了同时满足精度和运算速度的要求，本次离心泵的H-Q曲线采用2次多项式拟合[11]。

（3）编程

编程过程同幂函数拟合。

（4）求解并检验拟合误差

4 离心泵H-Q曲线指数函数拟合

用LOGEST函数来实现H-Q指数函数拟合[12⁃14]。

（1）拟合方程式建立

式中，b、m为待定系数。

（2）待定系数确定

在回归分析中，LOGEST函数可以计算出最符合数据的指数回归的拟合曲线。LOGEST函数语法形式为：

式中，数组known_y’s是扬程H的集合；数组known_x’s是数组流量Q的集合；const为一逻辑值，

TRUE表示指数模型中没有常数量,FALSE表示指数模型中有常数量；stats也为一逻辑值，指定时刻返回附加回归统计值，本文中将其设置为FALSE。

（3）求解并检验拟合误差

5 拟合案例分析

下面为3组出厂性能曲线H-Q数据，数据是从文献[15]的出厂性能曲线图中进行取点并加以整理形成表1。

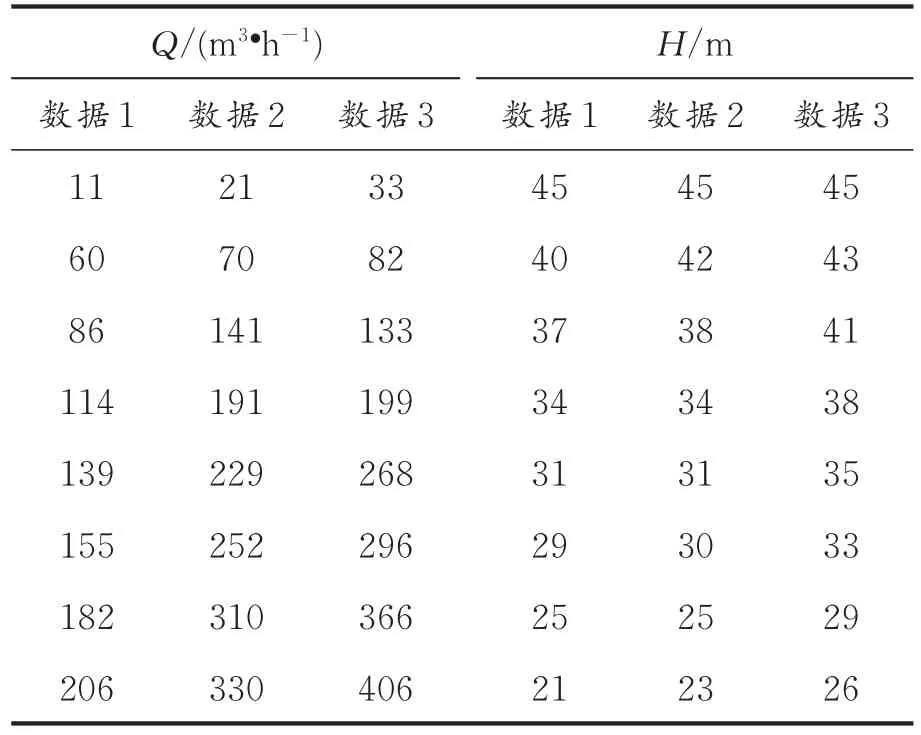
表1 出厂性能曲线数据Table 1 Factory performance curve data

根据实测数据及VB编程语言编制VB程序，以数据1的幂函数回归为例，VB程序界面操作界面（见图1）以及编写程序代码如下所示。

图1 数据1幂函数拟合VB界面图Fig.1 Power function fitting VB diagram of data 1

所编写的程序代码：

Private Sub Command5_Click()

Randomize

Dim x(100000)

Dim y(100000)

Dim M(100)

Dim n,j As Integer

n=InputBox('请输入坐标个数：')

For j=1 To n

x(j)=InputBox('请输入第'&j&'个点的横坐标')

sumx1=sumx1+x(j)^2

sumx2=sumx2+x(j)^4

y(j)=InputBox('请输入第'&j&'个点的纵坐标')

sumy=Val(sumy+y(j))

sumxy=sumxy+x(j)^2*y(j)

Text1.Text=(Text1.Text+(x(j)&','&y(j)))&vbCrLf

Next j

Picture1.Scale(-10,52)-(300,-5)

Picture1.DrawWidth=3

Picture1.Line(0,0)-(5200,0),vbBlack

Picture1.Line(0,520)-(0,0),vbBlack

Picture1.Circle(0,0),0,vbRed

For i=0 To 500 Step 50

Picture1.Line(i,0.3)-(i,0)

Picture1.Print i

Next i

For j=1 To n

Picture1.PSet(x(j),y(j)),vbBlack

Next j

For i=0 To 500 Step 50

Picture1.Line(0,i)-(0.3,i)

Picture1.Print i

Next i

Picture1.Scale(-10,52)-(300,-5)

a=(sumx2*sumy-sumxy*sumx1)/((n*sumx2)-((sumx1)^2))

B=(sumx1*sumy-n*sumxy)/(n*sumx2-((sumx1)^2))

For Q=0 To 250

H=a-B*Q^2

Picture1.PSet(Q,H),RGB(255,0,0)

Next Q

Text4.Text=Format(a,'0.0000')

Text5.Text=Format(B,'0.0000')

Text2.Text=CStr(Text4.Text)&'-'&CStr(Text5.Text)+'*Q^2'

For j=1 To n

M(j)=Text4.Text-(Text5.Text*(x(j)^2))

Wucha=Wucha+(Abs(M(j)-y(j)))/y(j)

Text3.Text=Wucha/n

Text3.Text=Format(Text3.Text,'0.00000')

Next j

End Sub

Private Sub Command6_Click()

Picture1.Cls

End Sub

根据最小二乘法原理结合VB编程语言，得出幂函数及多项式拟合，运用LOGEST函数对泵的H-Q性能曲线进行指数形式拟合，结果如表2和图2所示。

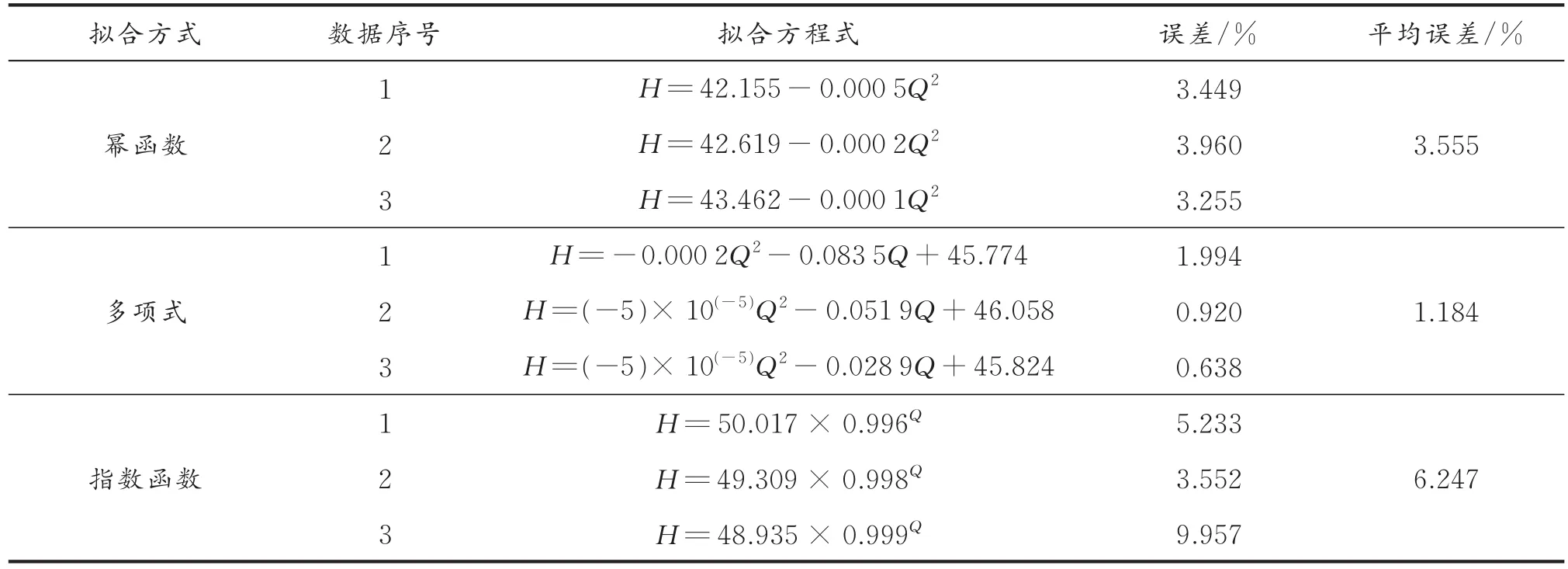
表2 拟合方程计算结果Table 2 Calculation results of fitting equation

根据表2拟合结果，多项式的拟合结果更精确，误差更小。因此用多项式的数学模型更能准确地表示离心泵H—Q性能曲线，为下一步出厂性能曲线校正提供基础。

6 H-Q性能曲线校正

在进行泵的出厂性能曲线拟合之后，由于离心泵在实际运行中会出现与设备厂家提供的性能曲线有一定偏差的现象，又因为泵的运行数据可能非常少且较密集，因此我们可以对出厂性能曲线进行上下左右移动来进行出厂性能曲线的校正。校正的方法也是最小二乘法。以多项式形式的出厂数据1得出的方程为例进行说明。

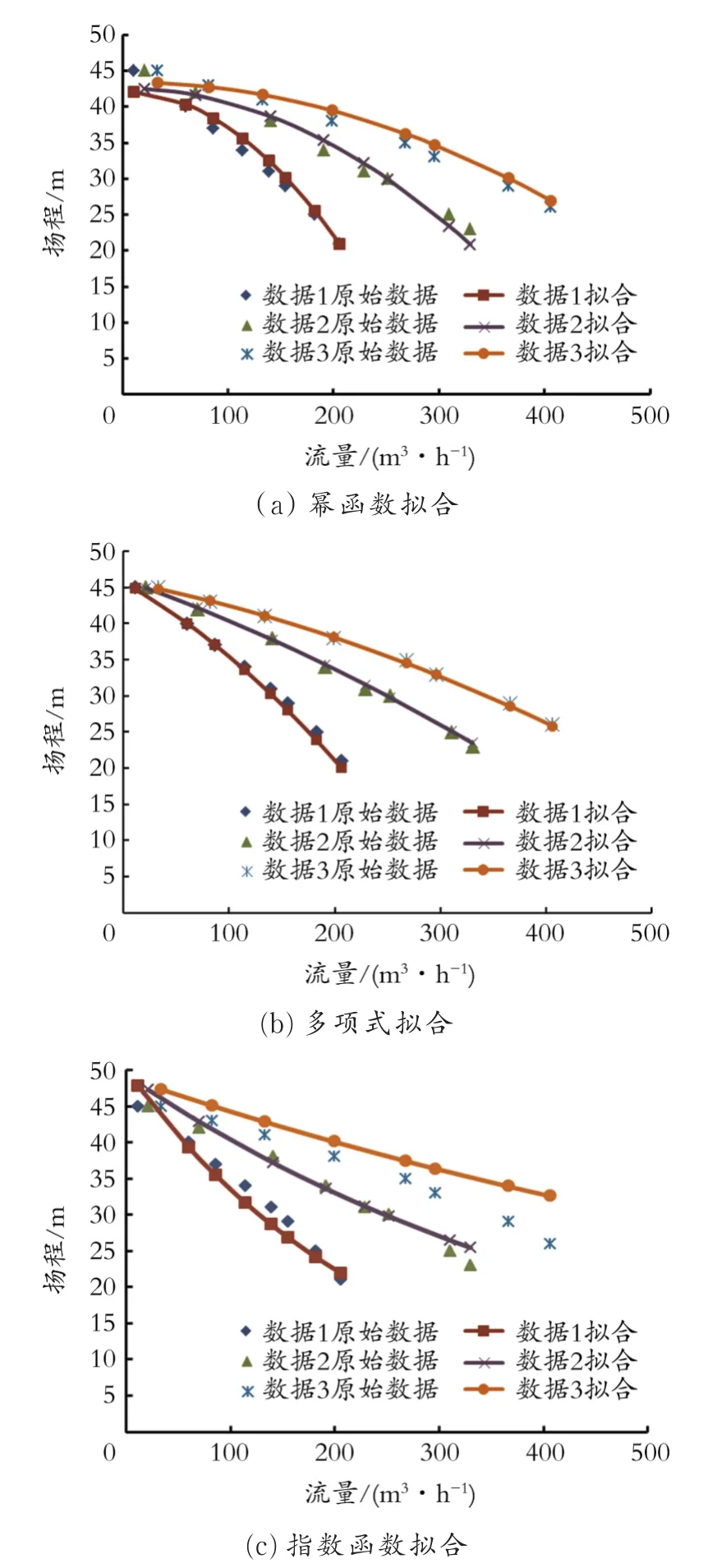
图2 各种函数拟合结果Fig.2 Different function fitting result

通过计算，得到泵的H-Q的出厂性能曲线为：

通过对(17)沿两个坐标轴正方向分别移动x与y单位，使扬程曲线尽量吻合实际运行数据所体现出的扬程特性。移动后的扬程曲线为：

通过最小二乘法计算，求出移动量x和y，使式（19）成立。

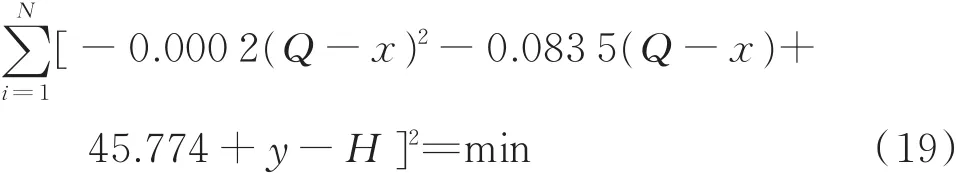
根据表1的工程实测数据，泵流量分别为12、60、86 m3/h，对应扬程分别为65、59、86 m。

通过运用VB对最小二乘法进行编程求解，如图3所示。

图3 校正拟合结果Fig.3 Correction fit result graph

由图3可得，校正后曲线方程为：

分析可得，校正后的曲线较之前向右平移了38.25个单位，向上平移了16.43个单位。校正之后的曲线方程与工程实测数据误差为2.2%。校正后曲线更加准确地拟合工程实际泵的性能，为后续开泵方案提供参考。

7 能耗分析

（1）能耗计算[16⁃17]

泵机组能耗分析指的是泵机组提供的扬程所消耗的电量。主要是为了补充管输原油流动过程的摩阻损失，泵机组t h的耗电量计算公式如下：

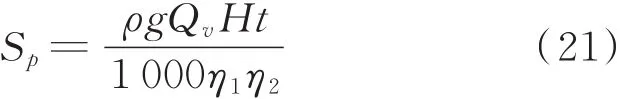
式中，Sp为耗电量，kW ⋅h；ρ为原油密度，kg/m3；Qv为管道的体积流量，m3/s；H为泵站总扬程，m；η1为电动机效率；η2为泵效率。

泵所需提供扬程为：

式中，H1为管道所需扬程，m；H为泵所需提供扬程，m。

加热炉能耗分析是指加热原油所损耗的油量，热力能耗主要是为了补充油品与环境大气所进行的散热。加热炉工作t h所消耗的油量计算公式如下：

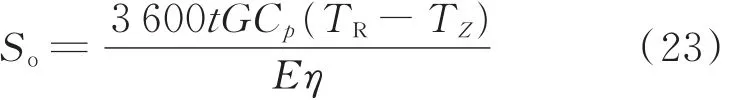
式中，So为耗油量，kg；G为原油质量流量，kg/s；Cp为原油比热容，kJ/(kg ⋅°C)；TR为热油出加热炉的温度，℃；Tz为热油进加热炉的温度，℃；E为燃料油低位发热值，kJ/kg；η为加热炉系统效率。

（2）能耗影响因素[13⁃14]

结合上述耗电量和耗油量的公式进行分析，能耗的影响因素为油品基本物性、管道运行工况以及泵或者加热炉的设备参数。

①油品基本物性。输送油品的密度、比热等参数均属于其基本物性参数，由于输送过程中油温对能耗影响相对较小，可取三分之一起点温度加上三分之二终点温度作为计算温度来计算能耗。

②管道运行参数。管道运行参数包括原油流量、进出站压力等参数。通过式（21）和式（23）可看出，流量越大，耗电量和耗油量越大。此外油品输量的变化也会对进出站油温有影响，主要是因为温度对油品黏度有较大影响，而黏度会对管道摩阻造成影响，因而造成耗电量和耗油量的不同。

③离心泵、加热炉参数。离心泵以及加热炉的参数对能耗有着直接的影响，比如泵效率、加热效率、泵扬程等参数，且泵效率或者加热效率越高，其能耗越低。离心泵中主要的参数就是离心泵的性能曲线，因此离心泵的性能曲线一定要准确，才能准确计算出后期能耗或者对未来能耗进行预测。

（3）实例分析

某工程由于沿线地温较高，油品温度均高于凝点，因此输送过程中无需开加热炉。通过上述分析可以看出，泵扬程、泵效率以及电动机的效率直接影响耗电量，且泵效率和电动机效率越大，耗电量越小。因此通过正确的拟合公式进行出厂特性曲线拟合并通过工程实际数据进行校正可以得出较为准确的耗电量，否则可能会多开泵，从而造成能源的浪费。

以上述数据1为例说明泵出厂特性曲线拟合公式校正对于能耗的影响。流量为82 m3/h，原油密度为845 kg/m3。

选用多项式函数进行泵出厂曲线拟合：当Q=82 m3/h时，根据上文的多项式拟合公式。H1=37 m，η1=72.8%，η2=85%。

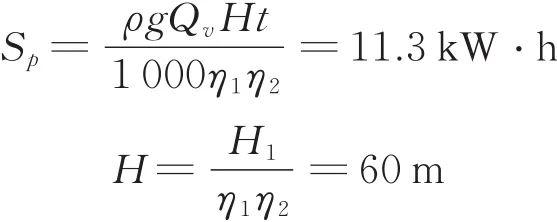
当Q=82 m3/h时，根据校正后的多项式拟合公式。H1=58.2 m，η1=73%，η2=85%。

假设一台泵能提供60 m的扬程，通过对校正前后所需扬程进行计算，没有校正时计算扬程为60 m，校正后为94 m。若采用没有校正时开泵方案设计，很有可能只开一台泵即可，但实际上一台泵远远达不到要求。由此可以看出，对泵进行出厂性能曲线校核是十分重要的。

8 结 论

（1）对离心泵进行测试的结果表明，在摩擦区时，H-Q曲线的幂函数拟合，多项式拟合差均在5%以内，但多项式的拟合误差更小，结果与曲线数据更接近。

（2）多项式拟合的方法可以推广到离心泵的流量-效率、流量-功率等曲线的拟合，经过反复试验，其拟合误差均较小。

（3）虽然只进行离心泵的数学模型拟合，但本方法同样适用于容积泵的特性曲线拟合，经过多次测试，拟合误差均较小。

（4）由于离心泵在实际运行中会与设备厂家提供的性能曲线有一定偏差，又因为泵的运行数据可能非常少且较密集，因此我们可以对出厂性能曲线上下左右移动来进行出厂性能曲线的校正。通过实例可以看出，对泵进行出厂性能曲线校核是十分必要的。