基于离散元的岩石单轴压缩实验模拟及断裂特性分析

李 玮，孟凡海，凌 鑫，李思琪，陈子贺

（东北石油大学石油工程学院，黑龙江大庆163318）

单轴抗压强度作为岩石的抗压强度的重要物理学指标，是研究岩石力学性质的基础。在岩石力学及相关的学科中被广泛应用。单轴压缩变形破坏是一个复杂的过程，得到诸多研究者的重视。岩石单轴压缩的应力应变过程一般分为4个阶段,即岩体内部裂隙压密、弹性形变、塑性形变以及破坏[1]。应力应变曲线与裂纹数应变曲线表明,岩石在压缩过程中应力与裂纹增长具有一定的对应关系，即在应力峰值的30%~80%时，裂纹稳定增长；当应力达到峰值的70%~80%以后，裂纹开始加速增长[2]。在岩石的破坏形式方面，拉张破坏为主的观点得到了广泛的认同[3⁃6]。离散元应用于岩石力学可将岩石颗粒间的连接看作是靠力链连接而成，在受力的状态下力链因断裂而发生弯曲，方向由柱状逐渐变成环状[7]。胡光辉等[8]考虑岩石的时效变形损伤过程，引入岩石细观单元时效损伤的应力腐蚀模型，建立了基于离散元方法的岩石时效变形损伤破裂模型，并通过单轴压缩及单轴蠕变的室内实验和数值模拟对比验证了所建立的时效变形损伤破裂模型的合理性。

随着计算机的快速发展，应用数值模拟对岩石的力学实验进行仿真模拟变得越来越普遍，离散元软件的发展使通过离散元方法模拟岩石的力学实验变得越来越简便。离散单元法能够从宏微观层面上对数值模拟结果进行分析，因此，该方法在岩石的数值模拟中也得到迅速的推广和应用[9]。本文借助离散元软件，采用Hertz⁃Mindlin黏结接触模型模拟大庆三肇地区深层岩石在受到单轴压力的作用下的断裂特性，分析其受力性质，并结合离散元理论分析基于力链的颗粒体系接触应力。与单轴压缩室内真实实验对比，通过离散元数值模拟的优势在于可以在微观的角度观察到岩石的破坏特性。

1 室内单轴实验

1.1 岩石试样制备及实验设备

本文采用20 t级单轴实验机进行单轴压缩实验，如图1所示。实验所用的岩样均取自大庆三肇地区深层岩石，并制备成直径20 mm、高度40 mm的圆柱形试件，加工好的岩心试件如图2所示。

图1 单轴压缩实验机Fig.1 Uniaxial compression testing machine

1.2 实验结果分析

实验前将岩石两端面涂抹适量的黄油。选取加载速度为0.2 mm/s。选取平均100 s的加载时间，进行12次实验，为获取单轴抗压强度与岩石基本参数，选取实验结果较合理的3、8、10、12的4组试样进行研究，结果如图3所示。

由图3可以看出，在达到压缩力峰值前表现为弹性压缩,在峰值附近有小部分的回弹现象，样品应力在峰值后迅速下降，塑形变形不明显，表明该泥质砂岩脆性较强。当试件抗压强度达到极限以后，轴向力⁃轴向变形曲线有一小段的下降紧接着出现一个峰值。这种现象一般是因为发生弱剪切面破坏，在接近试件上端面位置发生轻微破碎，并且直接造成试样整体破坏，所以紧接着上压板接触到残余的试样，从而再次出现一个峰值。

图2 实验用岩心试样Fig.2 Core sample for experiment

图3 压缩力-轴向变形曲线Fig.3 Compression force axial deformation curve

2 离散元的基本原理与力学模型建立

2.1 离散元法基本原理

离散元法的基本原理是：将研究对象划分为相互独立的一个个单元，根据单元之间的相互作用以及牛顿运动定律，采用静态松弛法或动态松弛法等迭代方法进行循环迭代计算，确定在每一个时间步长所有单元的受力及位移，并更新所有单元的位置[10]。通过对每个单元的微观运动对离散单元进行跟踪计算，从而得到整个研究对象在宏观方面的运动规律。根据离散元基本原理的定义，单元间相互作用的规律通常被当作是瞬态平衡的问题，定义只要对象内部在多种作用力的条件下达到平衡状态，就认为其处于平衡状态。离散元法的离散单元从几何形状上可分为颗粒元和块体元两大类。块体元中以四面体元、六面体元为主要的离散单元，对于二维的离散元单体问题可以是任意多边形元，但应用的范围比较单一，而且每个离散单元的单体都具有一个基本的节点(通常取形心点)。在模拟过程中，主要采用球体元作为离散单元，对于二维问题的离散元问题一般采用圆盘形单元作为离散单元。

岩石作为非均质物质，在受力过程中具有复杂的变化，有限元通过画网格的方式模拟岩石，在模拟岩石的受力破坏过程，不能准确反映岩石的性质。通过离散元的方法，将岩石离散成一个个颗粒，利用有限尺度的黏合剂黏结起来，这种黏结与实际岩石结构相似，通过黏结阻止颗粒的切向和法向相对运动，当达到最大法向和切向应力时，这种黏结就会发生破坏，在破坏后颗粒作为刚性球体彼此相互作用，这种黏结模型与混凝土及岩石的结构相似，特别适合模拟岩石结构。

2.2 接触模型建立

为了准确反映岩石的性质，应用Hertz⁃Mindlin黏结接触模型对岩石试样进行单轴压缩实验与模拟仿真，通过与真实实验对比，对参数进行校核。接触模型的黏结约束产生的合力在两球形相交界面的中心（见图4），在特定的时刻颗粒被黏结起来，在此之前颗粒通过默认的Hertz⁃Mindlin接触模型产生相互作用[11]。

图4 岩石颗粒接触模型Fig.4 Contact model of rock particles

进行单轴压缩室内实验材料物性参数见表1。根据模拟要求对材料间的接触参数进行设置，材料之间的静摩擦因数0.25，滚动摩擦因数0.80，恢复系数0.05；材料与钢板之间静摩擦因数0.50，滚动摩擦因数0.50，恢复系数0.02。

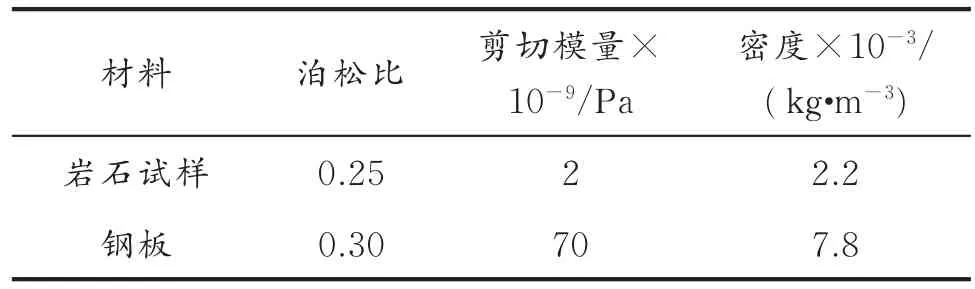
表1 材料物性参数Table 1 Material parameters

2.3 单轴压缩实验模型建立

模拟岩样如图5所示，其中上下平板为钢制材质，上侧钢板以特定的速度进行匀速运动模拟加压板对模拟岩石样本进行压缩，用以模拟单轴压缩实验的压力，其中下侧模拟钢板为固定状态，用来保证模拟岩石在受到模拟压力的作用下，下端被固定且无相对运动。

图5 模拟岩样示意Fig.5 Schematic diagram of simulated rock sample

选取4组较理想的实验结果取平均值，进行虚拟实验标定。在EDEM软件中,随机岩石颗粒半径由R0与倍率Cf相乘获得，随机岩石颗粒接触半径由R0'与倍率Cf相乘获得。岩石颗粒黏结参数如表2所示。颗粒开始进行黏结的时间为0.12 s。仿真时，固定时间步设置为1×10-6，初始仿真总时间为0.40 s，可根据具体时间实时进行调整。EDEM的颗粒工厂可以根据用户需要进行定义，将编译的dll文件导入颗粒工厂中。生成的岩石单轴压缩仿真模型（黏结键分布）如图6所示，生成的颗粒数为4 880，颗粒黏结键数为16 000，平均每个颗粒与周围3.4个颗粒生成黏结键，该模型黏结充分。

2.4 模拟实验结果

模拟实验结果如图7-10所示。

表2 岩石颗粒黏结参数Table 2 Cohesive parameters of rock particles

图6 黏结键分布Fig.6 Distribution of bond bond

图7 模型受力破坏示意Fig.7 Schematic diagram of stress failure of model

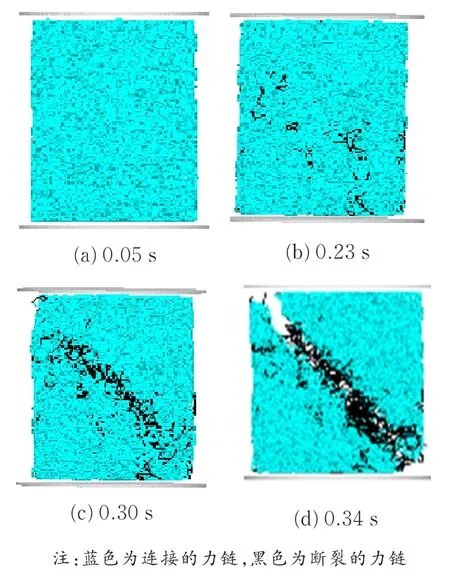
图8 模型受力力链断裂示意Fig.8 Schematic diagram of stress chain fracture of model

通过颗粒流中的球状模型，借助离散元软件可以很好地模拟出岩石在单轴压力作用下断裂的过程，通过离散元软件的后处理功能给不同速度的离散元颗粒按照速度属性的不同进行分类着色（见图7、8），模拟单轴压缩实验的模拟总时间为0.40 s，根据模拟结果绘制应力时间曲线（见图9），可以看出不同的变形特性下颗粒的受力具体值及在受到单轴压力的作用下力的变化趋势。

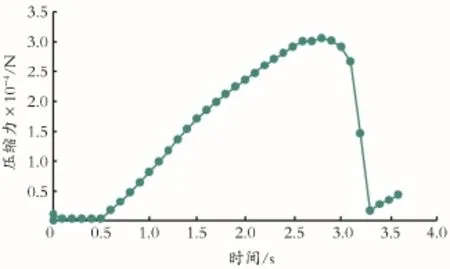
图9 压缩力与时间关系Fig.9 Compression force time diagram

图10 黏结力链数目与时间关系Fig.10 Time graph of the number of cohesive force chains

岩石在承受单轴压力过程中的第一个阶段为岩石的裂缝压密阶段，真实单轴压缩实验时仅通过实验结果曲线不能揭示真实的岩石颗粒压密的变化情况，通过离散元软件可以看出在0.05 s有少数几个颗粒具有较大速度，即岩石有被破坏的趋势。通过图8（a）可以看出，此时仅有极少数力链有断裂的现象而且力链的方向与轴向载荷的方向相同。第二阶段为力链断裂键的增长阶段，从图8(b)可以看出，此时较多颗粒有较大的速度，较多力链发生断裂，此时模拟岩石试样即将发生断裂，但未达到岩石屈服极限，因此应力继续增大。此时的应力达到峰值的81%左右，在此阶段断裂力链的数目增长较快，但增长速度比较平稳，应力时间曲线斜率近似为固定值，说明模拟岩石试样脆性较高。第三阶段为岩石试样完全开裂阶段，从图8（c）可以看出，此时岩石将要断裂，在断裂位置有较多的颗粒具有较大的速度，断裂位置的力链多数发生断裂，应力达到极限，应力时间曲线斜率近似为直线，岩石试样完全被破坏。第四阶段为到达峰值后应力急速下降过程，从图8（d）可以看出，此时模拟岩石试样完全断裂，两部分断裂位置具有相对速度，断裂力链数目不再增加（见图10），宏观上能直接观察到试样的破坏状态。可以与单轴压缩室内实验对比，结果如图11所示。

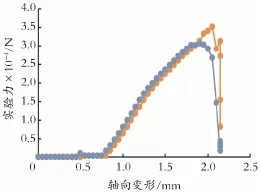
图11 真实实验与模拟实验对比Fig.11 Comparison curves between real and simulated experiments

由图11可以看出，首先在缩容段，室内实验曲线与模拟曲线完全重合，此时主要是将岩石微小的裂缝被压实的过程，因此，按照本文方法建立实验模型在较小的颗粒状态下可以较准确模拟出岩石空隙情况，在弹性形变过程中，两个曲线并没有完全重合，但是两种曲线近似平行，与岩石的力学性能符合，对比塑性变形过程可以看出两条曲线具有微小的差异，但是差异在可接受的范围，在最后的扩容阶段，室内实验具有一个峰值，在模拟结果中未有此种现象发生，这是由于室内实验最初在上端面发生破碎，当最上面发生破碎时试样压缩力迅速下降，而在模拟过程中岩石在试样中间发生断裂，且压缩力的变化过程较慢。

3 结 论

以颗粒离散元法为理论基础，采用Hertz⁃Mindlin黏结接触模型作为被压缩材料，通过对仿真物理模型的影响因素的分析，并与室内实验的结果进行对比，证明了模拟结果的可靠性。

（1）通过单轴压缩室内实验得到岩石材料参数、接触参数，通过虚拟参数标定模拟出具有和大庆三肇地区深层岩石相似力学性质的岩石。

（2）通过与单轴压缩真实压缩实验的对比，即与真实单轴压缩实验应力应变的曲线进行拟合，在完全破坏前也具有回弹现象发生，模拟实验与真实实验的拟合度较高，可以通过EDEM模拟单轴压缩真实实验。

（3）通过模拟典型岩石脆性破坏过程，得力链在受力破裂之前没有较大的变形过程，破坏形式为直接断裂，也就是说这些岩石在荷载作用下没有显著觉察地变形就突然破坏，产生这种破坏的原因可能是岩石中裂隙的发生和发展的结果。