自升式风电安装船在不同土质插桩深度研究

包彩虹，王俊杰

（中交三航（上海）新能源工程有限公司，上海 200137）

0 引言

近年来，海上风能作为一种新的可再生能源，受到了大多数国家的青睐。《风电发展“十三五”规划》中明确指出：到2020年底，风电累计并网装机容量确保达到2.1亿kW以上，其中海上风电并网装机容量达到500万kW以上。因此，海上风电场的建设成为国家能源结构转型过程中必不或缺的一部分。而自升式风电安装船作为海上风电施工的专用船舶，也越来越多受到人们的关注。

自升式风电安装船主要通过将桩腿插入海底持力层，顶升船体出水形成一个在海平面以上的稳固安装平台来进行作业。与石油钻井平台不同，风电安装船具有“快插、快拔”的特性，而桩靴基础在不同土质中的承载能力也具有很大差异。因此，对不同性质的海底土承载力的计算以及平台基础入泥深度的预测是保障海上风电安全施工的重要前提，对风电安装船“站得住、拔的出”具有重要的指导意义。

自升式风电安装船插桩深度预测的关键在于地基土极限承载力的计算，一般把自升式风电安装船桩腿的最大预压载荷等于或小于地基极限承载力时所达到的入泥深度定义为插桩深度[1]，通过选取几个土层层位（文中所选层位为3～4层，根据土质特征进行判断选取），计算每个土层底面的地基承载力，找到桩腿最大预压载荷等于地基承载力时所在的土层深度来获得。文中主要采用《SNAME》[2]和《海洋井场调查规范》修正公式[1]对地基土极限承载力进行计算。

1 《海洋井场调查规范》修正公式

目前国内对于自升式船插桩深度的计算主要参考了SY/T 6707—2016《海洋井场调查规范》[3]的计算方法，通过假设插桩时桩靴基础上部土地完全回填（砂土）或完全不回填（黏性土）来计算该土层的地基极限承载力[1]。

1）对于不排水条件的黏性土，内摩擦角φ=0°，桩靴极限承载力公式为：

式中：qu为地基极限荷载；cu为土体强度指标；Nc为承载能力系数；γ1为桩靴基线以上土的有效重度；D为桩靴顶面没有覆土回填时取海底泥面到桩靴基线的距离，桩靴顶面被覆土回填时取桩靴平均厚度h。

2）对于砂质土，由于极限垂向承载力大[4]，因此考虑桩靴顶面被完全覆土回填，主要计算公式见为：

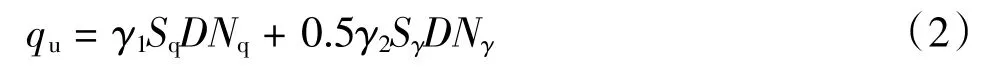
式中：qu为地基极限荷载；Nq，Nγ为承载能力系数，根据土体内摩擦角按太沙基极限承载力系数表确定；γ1为桩靴基线以上土的有效重度；γ2为桩靴基线以下深度B内土的有效重度；B为桩靴宽度；Sq，Sγ为桩靴底面形状系数，对于长方形桩靴Sq取1，Sγ取0.8。

3）对于粉土，考虑砂土和黏粒土的成分占比，一般通过土工试验进行确定，表现为排水性时，按砂土承载力公式进行计算，表现为不排水性时，按黏土承载力公式进行计算。

2 《SNAME》修正公式

《SNAME》相关规范通过将传统桩靴基础等效成圆盘模型[2]，并进一步考虑桩靴基础的上覆土层压力，从而计算基础在不排水黏性土和排水性砂质土中的垂向承载力。等效模型见图1。

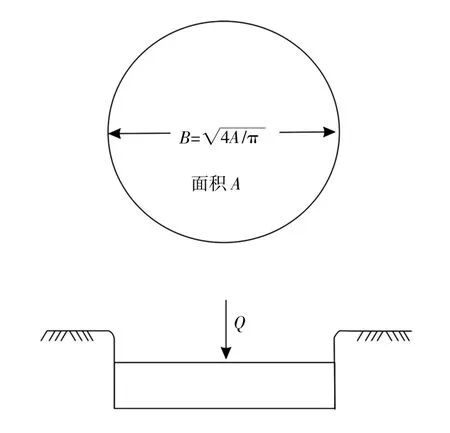
图1 等效模型Fig.1 The equivalent model

另外，本规范还对影响桩靴基础承载能力因素进行了分析，主要包括极限桩坑深度和深度系数，《SNAME》中采用稳定系数法来评估桩靴基础在黏性土中插桩的临界桩坑深度，但由于没有考虑土体回流效应，因此文中采用Hossain提出的极限桩坑深度计算方法[5]，其计算公式见式（3），深度系数计算方法则在后面不同土质中分别讨论。

式中：H为极限桩坑深度；B为桩靴等效横截面直径；Su为土体不排水抗剪强度；γ′为土体的有效容重。

1）对于不排水条件的黏性土，其垂向地基极限承载力为：式中：Fv为桩靴基础垂向地基极限承载力；cu为泥面D+B/4深度内土体不排水抗剪强度；Nc为承载能力系数，取5.14；Sc为桩靴形状系数；dc为垂向承载力深度系数；p0′为有效上覆压力；A为有效横截面面积。

在不排水条件的黏性土中，《SNAME》规范通过结合Meyerhof[6]和Brinch Hansen[7]的研究成果，以D/B=1为分界点计算垂向承载力深度系数，但戴兵等人通过相关实验发现现有的深度系数低估了桩靴基础的垂向承载力[8]，因此文中采用Gourvenec提出的深度系数计算方法[9]，其公式为：

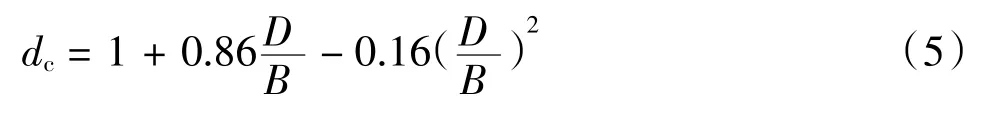
式中：D为桩靴基础入泥深度；B为桩靴等效横截面直径。

2）对于排水条件的砂土，其垂向地基极限承载力为：

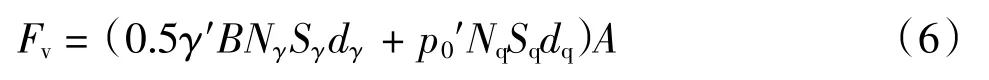
式中：Fv为桩靴基础垂向地基极限承载力；γ′为土体的有效容重；B为桩靴等效横截面直径；Nγ，Nq为承载能力系数；Sγ，Sq为桩靴底面形状系数；dγ，dq为垂向承载力深度系数；p0′为有效上覆压力；A为有效横截面面积。

其中垂向承载力深度系数dγ取值1，dq计算公式为：

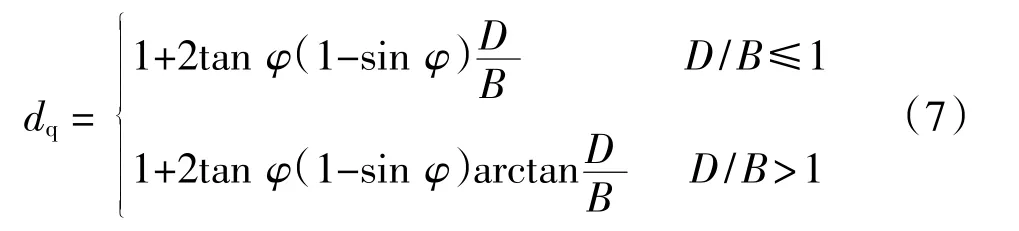
式中：φ为土体内摩擦角。

由于《SNAME》规范只考虑了带桩靴基础的垂直极限承载力，而忽略了桩靴上部土体回填和桩靴基础排开土的有效重力，因此文中在进行不同土质地基极限承载力计算时还需考虑这两部分的受力情况，从而得到自升式风电安装船在各个土层的插桩深度，其计算公式为：

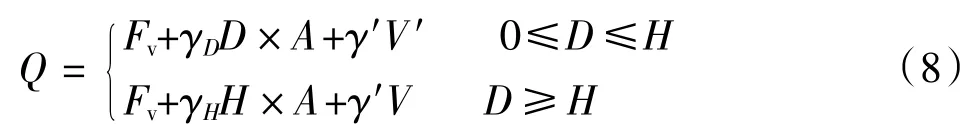
式中：Q为桩靴基础总的极限承载力；γD为从泥面到插桩深度的土体平均有效容重；γH为从泥面到极限桩坑深度的土体平均有效容重；γ′为土体的有效容重；V′为桩靴下部排开土的体积；V为桩靴基础体积。

3 实例分析

通过选取华能如东300 MW海上风电场和江苏响水200 MW海上风电场项目，分别利用文中所介绍的两种公式对这两个风场区域内相关机位进行自升式风电安装船插桩深度的计算，与实际插深进行比对，从而分析这两种公式在不同土质中的适用性。

自升式风电船—“三航风华”号主要参数见表1，桩靴基础见图2。

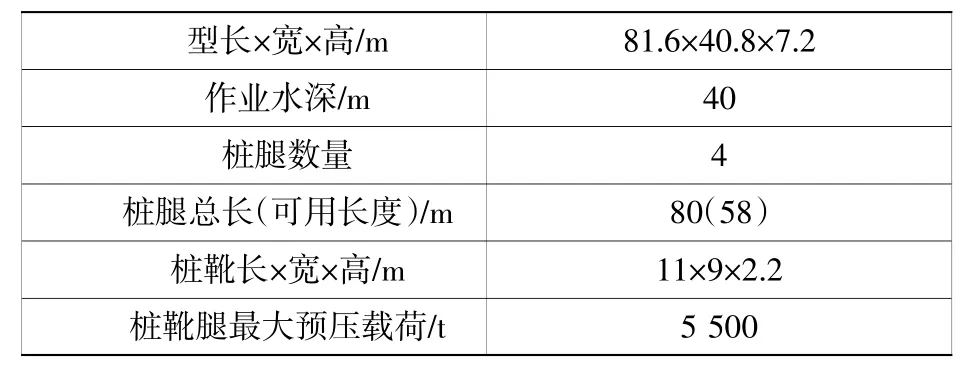
表1 “三航风华”号主要船型参数Table1 Main parametersof"San Hang Feng Hua"ship

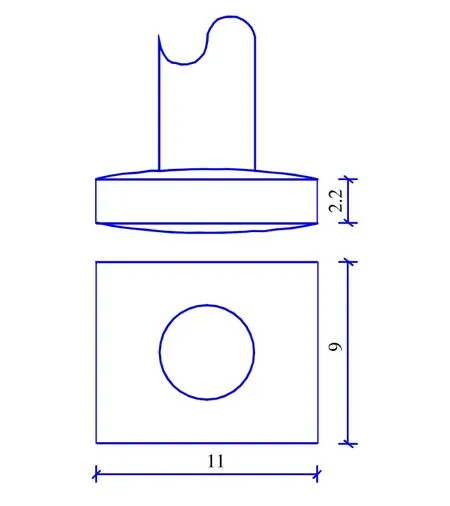
图2 桩靴基础图Fig.2 The drawing of pile-shoe foundation

3.1 华能如东300 MW海上风电场项目

海上风电场项目位于江苏省如东县的烂沙海域，海底地形变化较大，风电场形状呈不规则四边形，风场中心离岸约23 km。风电场拟安装38台上海电气4.0 MW、12台远景能源4.2 MW以及20台重庆海装5.0 MW风电机组。其中37～50号风机采用“三航风华”号进行安装。

现选取48号机位作为典型机位，48号机位土层相关参数见表2。分别采用《海洋井场调查规范》和《SNAME》修正公式，计算“三航风华”号插桩深度，具体数据见图3。

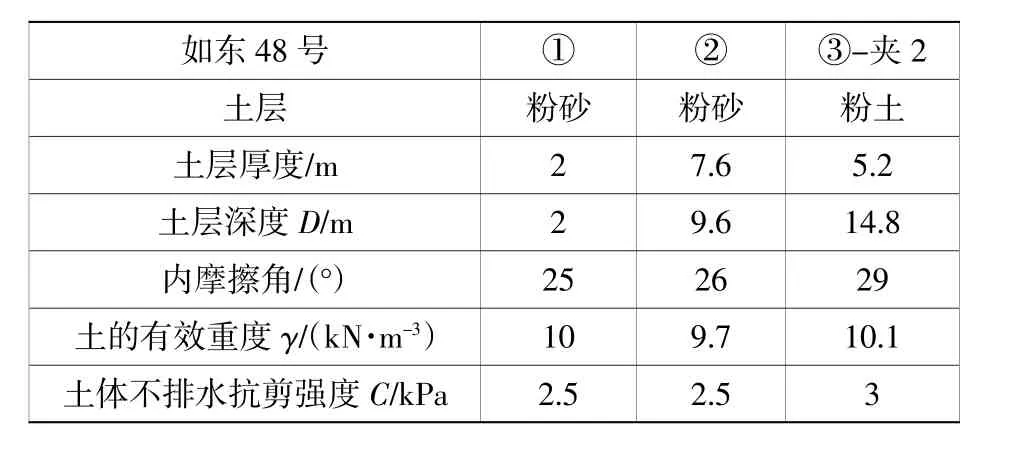
表2 48号机位土层参数Table2 The soil parametersof No.48 wind turbine position

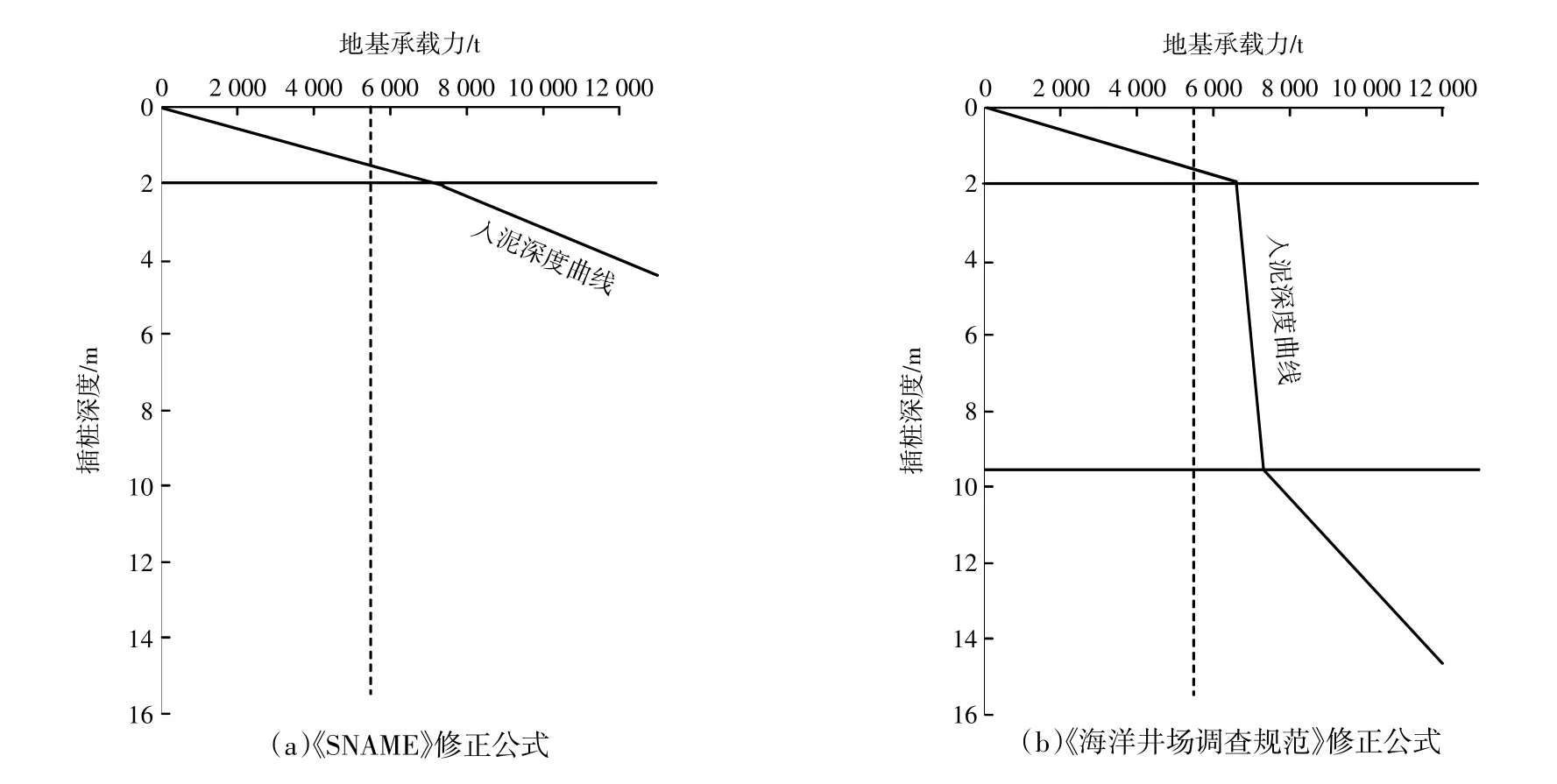
图3 48号机位插桩深度对比Fig.3 Comparison of the plug-in depth of pile in No.48 wind turbine position

由图3可知，采用《SNAME》修正公式计算出的地基承载力为5 500 t时，桩靴入泥深度为1.52 m；《海洋井场调查规范》修正公式计算出的地基承载力为5 500 t时，插桩深度为1.7 m，“三航风华”号实际插深为1.5 m。对比图3（a）、（b）可知，从第二层土层（2 m后）开始，入泥深度曲线发生明显差异，经分析发现《海洋井场调查规范》在砂质土的计算中，考虑砂质土垂向承载力极大，桩靴顶面被完全覆土回填，公式中D取值为桩靴平均厚度，但本次计算了3个砂性土层的地基承载力，而自升式平台桩腿的最大预压载荷为5 500 t，因此运用《海洋井场调查规范》所计算出的第②-③层的入泥深度曲线不具备实际应用价值。为进一步研究，本文又选取了4个机位分别对4个桩腿的插桩深度进行计算，其插桩深度计算结果见表3。

考虑到自升式风电安装船4个支腿预压载荷各不相同，且所处地质环境也可能存在明显差异，因此根据“同一机位，随着预压载的减小，其插桩深度也愈小”的原理，对存在明显误差的数据进行剔除，进而对计算结果进行相关性分析，相关性计算公式为（9）-（10），所得计算结果见图4。

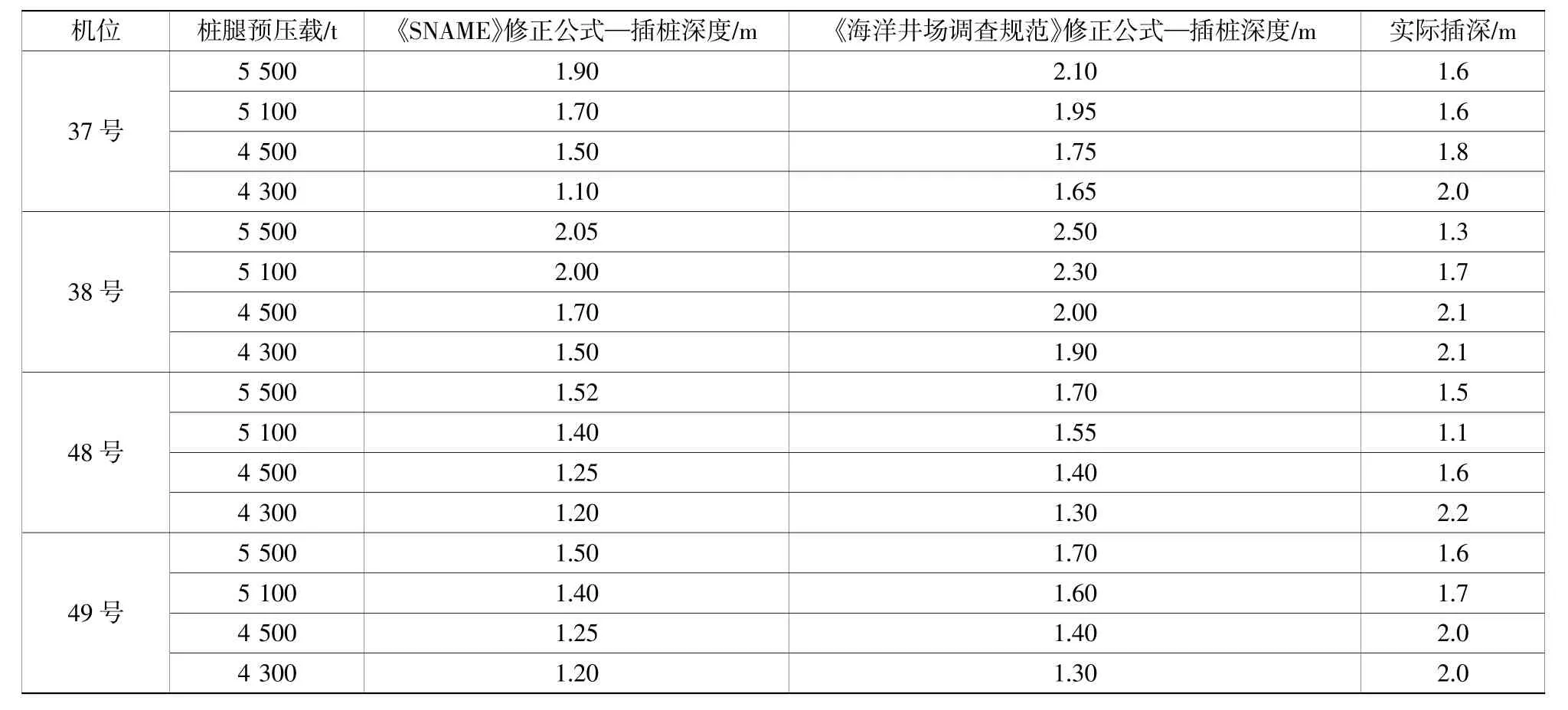
表3 两种公式插桩深度计算Table 3 Calculation of the plug-in depth of pile about two formulas

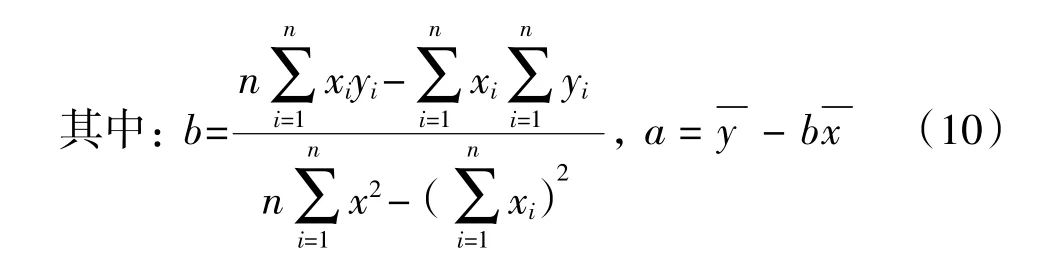
式中：x为理论插桩深度；y为实际插桩深度；a为修正系数；b为表相关性系数；当b越接近1且a越接近0时，x对y相关性越好，即理论插桩深度越接近实际插深。

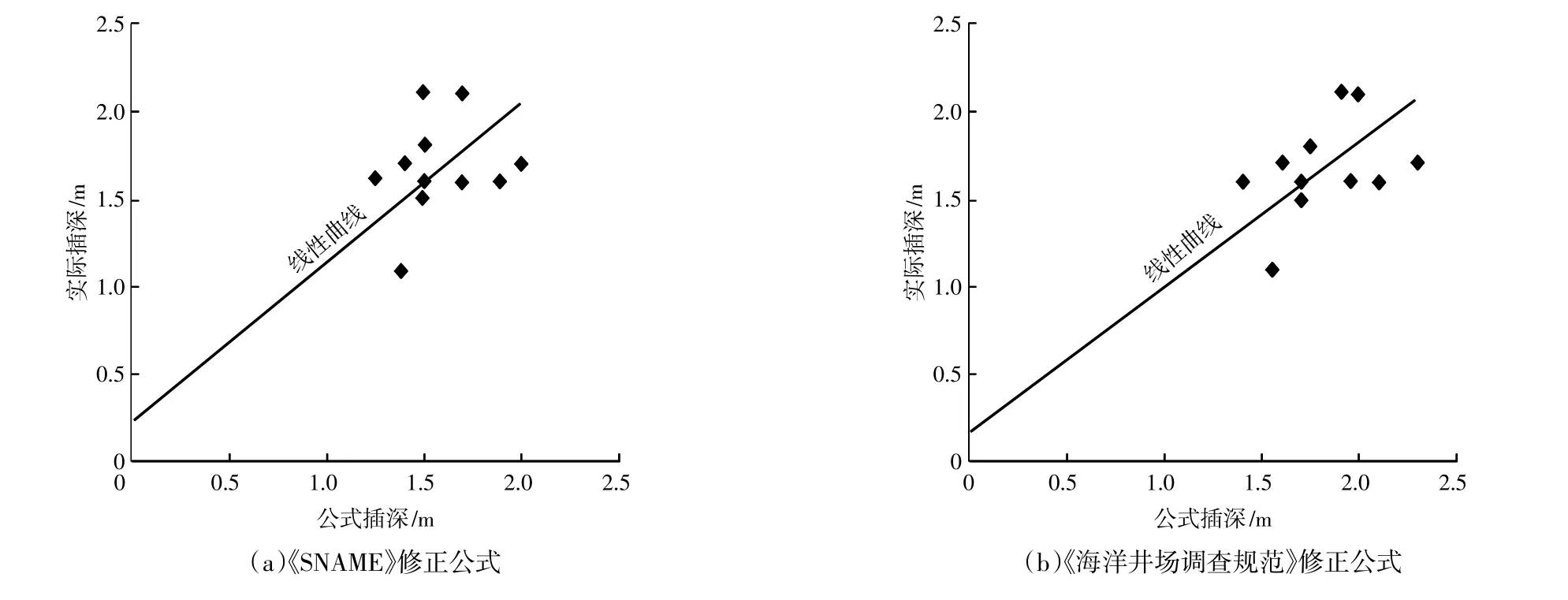
图4 如东风场两种公式计算值与实际插深相关性对比Fig.4 Thecorrelation contrast of calculated valuesand actual plug-in depth of pilewith two formulasin RUDONGwind farm

由计算结果可知：《SNAME》修正公式a值等于0.21，b值等于0.92，而《海洋井场调查规范》修正公式中a值为0.16，b值为0.83，则认为在排水条件的砂质土中，《SNAME》修正公式和《海洋井场调查规范》修正公式均可适用。

3.2 江苏响水200 MW海上风电场项目

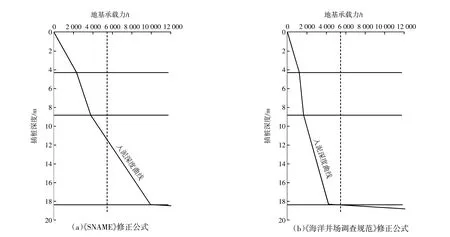
图5 18号机位插桩深度对比Fig.5 Comparison of the plug-in depth of pile in No.18 wind turbine position

江苏响水风电场项目位于响水县灌东盐场，三圩盐场外侧海域，风电场离岸距离10 km，沿海岸线方向长13.4 km，垂直于海岸线方向宽2.6 km，场区面积34.7 m2，水深8～12 m。本项工程总装机容量200 MW，采用西门子4 MW和金风3 MW风电机组进行安装。

现选择18号机位作为典型机位，分别采用《海洋井场调查规范》和《SNAME》修正公式进行计算，计算“三航风华”号插桩深度见图5。18号机位土层相关参数见表4。

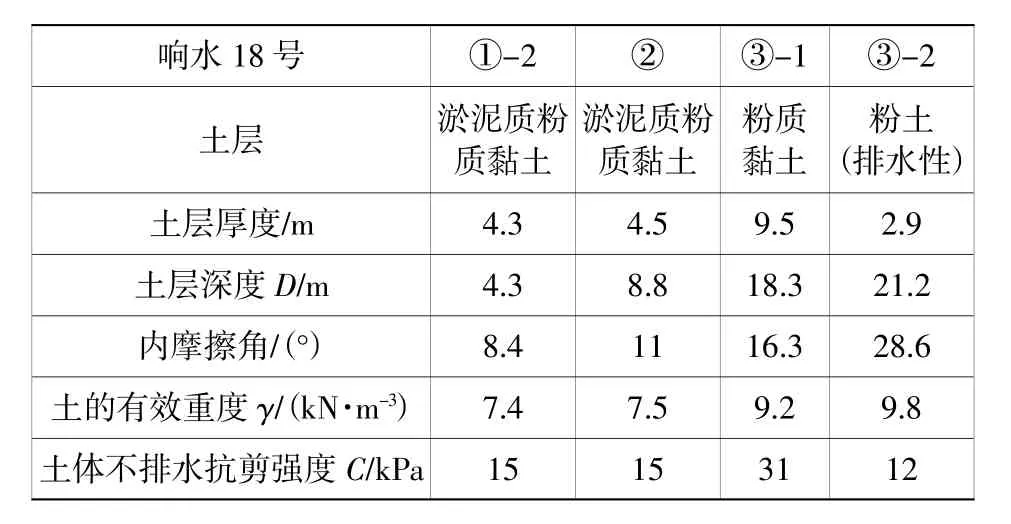
表4 18号机位土层参数Table4 Thesoil parametersof No.18wind turbineposition

由图5可知，使用《SNAME》修正公式计算出的地基承载力为5 500 t时，桩腿插入泥土深度为11.6 m，《海洋井场调查规范》修正公式在地基承载力为5 500 t时，桩腿入泥深度为18.4 m，“三航风华”号实际插深为12 m。为进一步研究公式的普遍性，本文又在响水风电场选取了4个机位，并分别对4个桩腿的插桩深度进行计算，其插桩深度计算结果见表5，通过选取表5中所计算出的两组数据，进行理论插深与实际插深的相关性分分析，得到相关性曲线见图6。

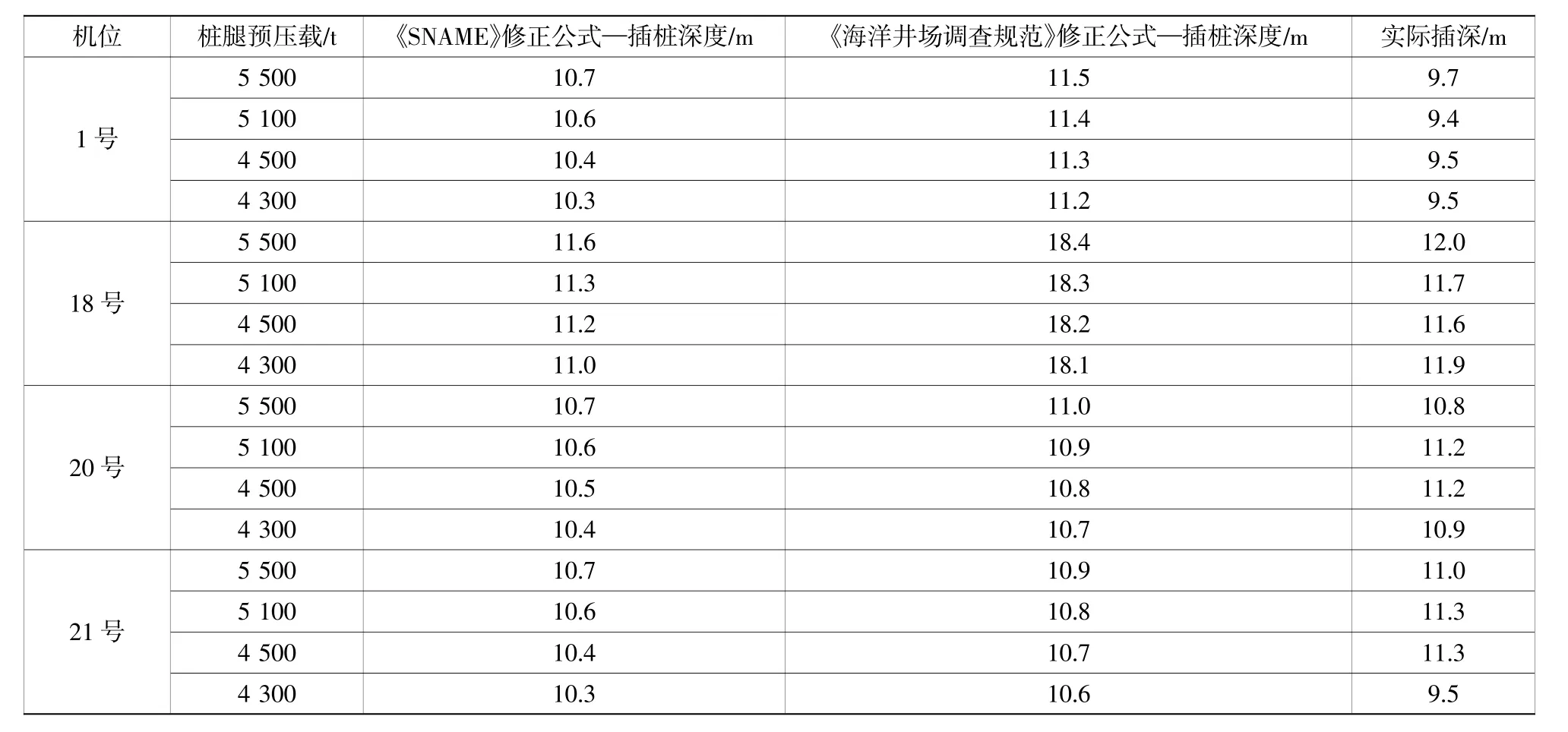
表5 两种公式插桩深度计算Table5 Calculation of theplug-in depth of pile about two formulas

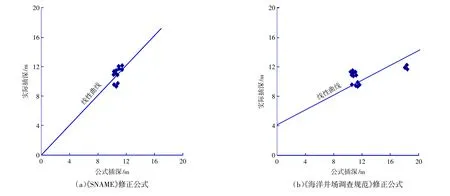
图6 响水风场两种公式计算值与实际插深相关性对比Fig.6 The correlation contrast of calculated values and the actual plug-in depth of pilewith two formulasin XIANGSHUI wind farm

由计算结果可知：《SNAME》修正公式a值等于-0.13，b值等于1.02，而《海洋井场调查规范》修正公式中a值为4.09，b值为0.5，因此认为在不排水条件的黏性土层中，《SNAME》修正公式所计算出的插桩深度更具有适用性。

4 基于MATLAB建立的插桩深度软件

为了更为方便、有效地进行插桩深度的计算，本研究利用Matlab的图形用户界面（GUI）功能，编译了一款程序软件。基于该软件进行插桩深度计算，具有速度快、可靠性高等优点，很大的缩减了工作量。另外针对不同船桩腿参数以及土壤地质情况，该软件可做出相应的调整，具有普适性，进一步方便了插桩深度的研究。

5 结语

文章通过选取两种不同规范的插桩深度修正公式，分别应用于“三航风华”号在华能如东和江苏响水风电场施工作业，计算结果表明，在砂性土中，由于地基土承载力较大，砂质层基本为桩靴所在持力层，因此两种公式得到的插桩深度没有显著差异，而在黏性土层中，由于持力层需要到达较深的砂土层，土体回流影响较大，相关系数的选取也具有很大差异，通过与实际插深进行相关性分析，《SNAME》修正公式在该性质的土层更为适用。

此外，基于MATLAB建立了插桩深度计算软件，可适用于不同的风电安装船及工况，对于以后插桩深度的研究提供了方便。