多元认知培养灵活思维能力——《运用乘法运算定律解决问题》教学与思考

普布占堆 陈小霞

【教学内容】

人教版四年级下册第29页例8（1）。

【教学过程】

一、回顾已学的运算定律

师：（课前板书：运算定律）近段时间我们都在学习运算定律，谁能说一说我们学习了哪些运算定律？

生：我们学习了加法交换律、加法结合律、乘法交换律、乘法结合律、乘法分配律。

（根据学生问答板书）

师：这些运算定律的字母表示是怎样的？

生：加法交换律 a＋b＝b＋a；加法结合律（a＋b）＋c＝a＋（b＋c）；乘法交换律 a×b＝b×a；乘法结合律（a×b）×c＝a×（b×c）；乘法分配律 a×（b＋c）＝a×b＋a×c。

师：看来大家对前面有关运算定律的知识掌握得不错，这节课我们将进一步聚焦乘法运算定律，运用乘法运算定律来解决一些生活中的问题。

（板书完善课题：运用乘法运算定律解决问题）

【设计意图：运算定律是本节课学习的直接基础，课始安排复习环节，目的是唤醒所有学生的已有经验。由于这属于识记性的问题，绝大部分学生能正确回答，因此，在教学时建议将回答的机会留给学困生。如果有学生对运算定律的字母表示有困难，可以通过举具体例子的方法引导学生再次经历字母表示数的过程。】

二、解决羽毛球个数的问题

1.阅读与理解。

课件出示教材呈现的问题情境，如图1。

图1

师：观察这幅图，你能从中发现哪些数学信息和问题？

生：我发现了两条数学信息，分别是“5副羽毛球拍，花了330元；25筒羽毛球，每筒32元”。要我们解决的问题是“王老师一共买了多少个羽毛球？”。

生：还有一条信息“‘一打’是12个”。

（板书信息和问题）

师：要解决这个问题，应选择哪几条信息？

生：选择“25筒羽毛球、‘一打’是12个”这两条信息。

师：同意吗？能从众多信息中选择对解决问题有效的信息是解决问题的第一步。

【设计意图：“解决问题”教学强调让学生经历问题解决的全过程，即阅读与理解、分析与解答、回顾与反思。学生能否正确理解题意，找到解决问题所需要的相关信息，并找到它们之间的关系，是问题能否顺利解决的基础与关键。教学时让学生经历从情境中获取数学信息、从众多信息中选择对解决问题有效的信息的过程，目的是进一步培养学生阅读与理解的能力。】

2.分析与解答。

（1）独立思考，尝试解决问题。

师：怎么解决这个问题呢？请在草稿本上列出算式，并用喜欢的方法算一算。

（教师巡视，搜集典型的方法板书在黑板上）

方法1：

方法2：

选择2017年10月至2018年6月在南京医科大学附属无锡第二医院眼科检查确诊的NAION患者18例（18眼）作为NAION组。其中男8例，女10例。年龄38～78（60.5±10.6）岁，病程3.5～8.0（4.8±1.8）个月。

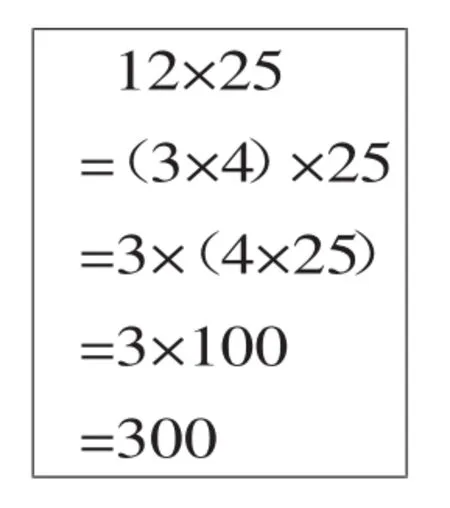
方法3：

（2）读懂过程，感悟不同方法。

师：黑板上的三种方法都能看懂吗？说一说，他们分别是怎么想的？

生：方法1是三年级时学的竖式计算；方法2把12拆成了3×4，后续的计算运用了乘法结合律；方法3把12拆成了10+2，后续的计算运用了乘法分配律。

师：解释得很正确，那除了这三种方法，你们还有别的方法吗？

生 1：12×（30－5）。

生 2：12×5×5。

生 3：12×（20＋5）。

生 4：（20－8）×25。

师：如果让你将这五位同学的方法写到板书的相应位置上，你会分别写在哪里？

生：12×（30－5）、12×（20＋5）、（20-8）×25 写在方法3的边上，因为它们都运用了乘法分配律，其他两种写在方法2的边上，都运用了乘法结合律。

生：其实竖式计算也运用了乘法分配律，竖式计算的过程和12×（20+5）的思路是一样的。

师：谁来边连线边说一说，竖式计算的过程和12×（20+5）的思路一样在哪里？

生：竖式的第一步是 12×5，第二步是 12×20，实际上就是把25拆成了20+5。

（3）分类比较，沟通不同方法。

师：那也就是说，刚才同学们提出的这么多种方法，实际上可以分成两类。（教师在板书中的两类方法之间划一条竖线）比较这两类方法，有什么相同点和不同点？

生：相同点是都对其中一个数据进行了拆分，不同点是一类是拆分成两个数相乘，运用乘法结合律解决，另一类是拆分成两个数相加，运用乘法分配律解决。

师：所有的方法都是对一个数进行拆分，你喜欢哪几种拆法？为什么？

生：我比较喜欢拆分后运用运算定律进行计算时能凑出整十、整百数的方法，这样能使计算变得更加简便。

【设计意图：分析与解答是解决问题的关键环节，本环节的设计力求利用教学的开放性培养学生思维的灵活性。让学生用喜欢的方法独立计算12×25，不同层次的学生会采用不同类型的方法。多种方法的交流，让学生在解读方法中经历了群体方法多样化和个体方法优化的过程，突破了个体学生的思维定势。比较沟通则让学生形成了寻求合理简洁的方法解决问题的意识。整个环节充分发挥了教师在教学中的主导作用与学生的主体作用。】

3.回顾与反思。

师：回顾一下，我们是怎么解决“王老师一共买了多少个羽毛球？”这个问题的？

生：我们先根据问题选择了需要的信息，对问题进行分析解答后发现，解决一个问题可以有多种方法，要根据数据特征找寻合理简捷的方法。

【设计意图：学生在解决问题的过程中，能否获得解决问题的一般方法与策略，能否连点成线形成知识结构，是学生解决问题能力维度中的重要指标。为了达成这一能力，本环节让学生回顾了解决问题的全过程，在回顾中强化方法、养成习惯。】

三、巩固练习

1.选择图1中的信息解决问题“王老师买羽毛球一共花了多少钱？”。

师：解决这个问题需要选择哪几条信息？

生1：选择“5副羽毛球拍，花了330元。买了25筒羽毛球，每筒32元。”

生2：选择“25筒羽毛球，每筒32元。”

师：有不同意见，你们同意谁的？

生：同意第二位同学的，因为问题问的是买羽毛球一共花了多少钱，只要选择与羽毛球相关的信息就可以了。

师：你是怎么解决的？

生1：

生2：

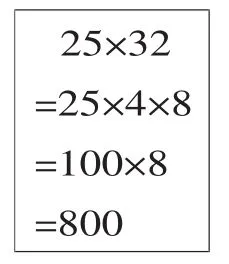
师：两种方法，你喜欢哪一种？为什么？

生：喜欢第二种，第二种简便。

师：看来大家已经能根据数据的特点，寻求合理简捷的运算途径解决问题了，为你们的进步点赞！

2.李大爷家有一块菜地，如图2。这块菜地的面积有多少平方米？

师：这个问题怎么解决？

生1：可以把这块菜地分割成两个长方形，21×9+19×9=360m2。

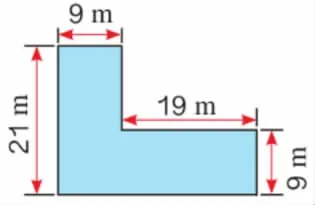
图2

生2：可以把分成的两个长方形拼成一个大长方形（如图 3），（21+19）×9=360m2。

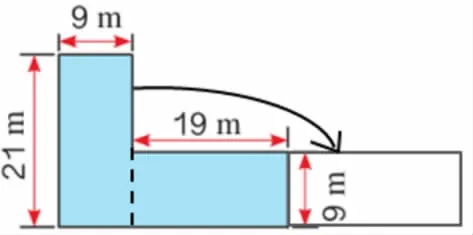
图3

师：观察这两种方法，你有什么发现？

生：21×9+19×9=（21+19）×9，实际上是运用了乘法分配律。

生：第二种方法计算比较简便。

【设计意图：本环节安排了两道练习，练习1与例题的情境相同，问题不同，让学生再次完整经历了解决问题的全过程。练习2是一个实际问题的解决，同时也是乘法分配律的典型几何模型，安排此题有两个目的，一是借助几何模型深化对乘法分配律的理解，二是在交流的过程中进一步培养学生思维的灵活性。】

四、谈收获，说疑问

师：通过本节课的学习，大家对运算定律有什么不一样的理解？

生：根据数据特点对数据进行拆分，运用运算定律进行计算，可以使计算变得简便。

师：那大家还有什么疑问吗？

生：在除法中有简便运算吗？

师：好问题，课后自己先研究，我们下一节课来交流。

【设计意图：谈收获是再一次对整节课进行回顾和提炼，以达成对方法和技能的进一步强化。提问题是培养学生的问题意识，通过提问激发学生进一步探究的欲望。】