凸显本质提升素养——兼评两节《倍的认识》教学设计

周卫东（特级教师）

章建跃博士指出：数学根本上是教概念的，数学教师是玩概念的。数学概念是数学知识的“细胞”，是进行逻辑思维的第一要素。一切数学规则的研究、表达与应用都离不开数学概念。数学概念是构成数学“四基”“四能”教学的重要内容，又是数学学习的核心所在。概念课是小学数学教学中的一种主要课型，数学概念教学是课堂教学最重要的环节之一。

无疑，“倍”是一个重要的数学概念。虽没能看到两则设计的“现场版”，但从字里行间的反复玩味中，可以感受到：殷芊老师的《关注本质 夯实概念》（后简称设计一）与姚晶晶老师的《促进学习真正发生》（后简称设计二）两则教学设计，在凸显概念本质、经历学习过程及提升数学素养等方面均有着许多值得广大同行学习与借鉴的地方。

一、追根溯源，厘清本质

美国著名的数学教育家赫斯认为：“数学教学的问题并不在于寻找最好的教学方式，而在于明白数学是什么，如果不正视数学的本质问题，便永远解决不了教学上的争议。”一般认为，数学知识的本质，既表现为隐藏在客观事物背后的数学知识、数学规律，又表现为隐藏在数学知识背后的本质属性。数学教学教什么？毋庸置疑，摆在第一位的肯定是教教学内容的本质。

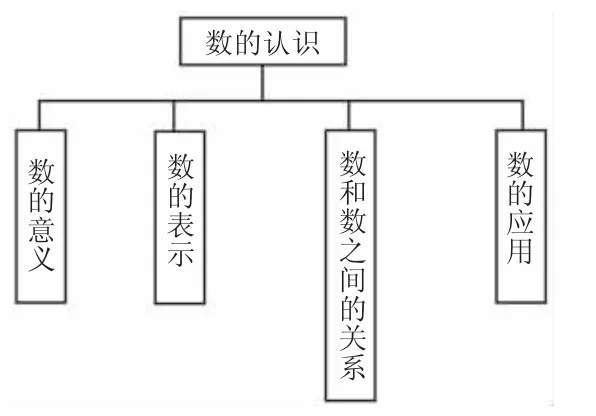
“倍”的知识在小学数学内容中有着十分重要的位置。荷兰著名数学家弗赖登塔尔指出：“数的概念的形成可以粗略地分成以下几种：计数的数、数量的数、度量的数和计算的数……，其中所谓‘度量的数’，就好比用勺子一次次舀空装满水的容器那样，用一个单位去量那个量。”这里，量得的结果就得到一个“倍”数。换一个角度来看，在小学数学教学内容中，“数的认识”包括数的意义、数的表示、数与数之间的关系和数的应用，而“数与数之间的关系”既包括数与数之间的相差关系，也包括数与数之间的倍数关系。“数与数之间的倍数关系”贯穿于小学学习的全过程，具体体现在“份”“除法”“分数”“比”“百分数”等知识中。可见，对知识结构而言，“倍”具有“种子”的作用，其本质是否清晰、是否牢固将直接影响到其他相关概念及概念体系的建构。

二、选准基点，引出概念

“盲人摸象”的故事告诉我们，尽管盲人们有各种准确的信息，却不能正确地认识大象。因而如果我们要教学生认识大象，一定是把他带到大象实体或者是大象的图片（影像）前，让他们有完整的认知。数学教学也应该这样：给学生一个现象，让他们接受完整而鲜活的数学信息。他们通过自己的信息采集和加工，从而形成的数学知识就是实在的也是容易牢固记忆的。

概念的引入有两种方式，即概念的形成和概念的同化。显然，“倍”知识的教学属于概念形成的教学。两则教学设计在准确厘清概念的本质特征后，都能朝向概念的“全貌”，围绕“两个量的比较”展开，很好地引导学生经历概念的形成过程。设计一围绕“蓝花有2朵，红花有6朵”，在学生提出“求和”“求差”两类数学问题之后，引出新的问题“除了比较多少，还有一种比较方法，今天我们就来学习这种特别的比较方法”，把2朵蓝花和6朵红花排成两行后，“像这样把2朵蓝花圈起来看作1份（边说边圈），那红花有这样的几份呢？”“蓝花有2朵，红花有3个2朵，我们就说红花的朵数是蓝花的3倍”，通过这样的方式，直奔中心、简洁明快地引出了“倍”的概念。而设计二则有着鲜明的儿童立场，把教学“安放”在学生经验的土壤之中。“之前，你们听过或者在哪儿见过‘倍’吗？它是用来表示什么的呢？”继而，出示三幅图，让学生辨析：“哪一幅图可以表示红花的朵数是蓝花的3倍？”此时，学生会充分调动自己的经验储备，试图对“3倍”进行辨析与解释，进而明晰：每幅图中都有“3”，只有第二幅表示的是3倍的关系，另外两幅图都是相差3个；“3倍”的意义和图3中每份“3个”的区别。

三、多元表征，促进理解

多元智能理论创始人加德纳认为：任何一个重要的、复杂的概念都可以运用多种方式来理解和表达。郑毓信教授则提出：应当帮助学生建立概念的多元表征，并根据需要与情境在表征的不同成分之间做出灵活的转换，使学生对数学概念有一个更深刻、更全面地认识与理解，培养学生思维的灵活性。

表征有不同的方式，可以是具体形象的，也可以是语词的或要领的。两则设计都能创造机会，较好地发挥表征在概念理解中的作用。设计一中，在学生理解了“倍”的基本含义之后，创设了“请你摆一摆，要求摆出的红花的朵数是蓝花的2倍”“如果是摆小棒呢？怎样摆才能使得第二行小棒根数是第一行的2倍？”的教学情境，让学生自由创编，进而明白：不管是红花、蓝花，还是小棒等不同的材料，也不管是两者数量如何变化，只要把其中一种当作1份，另一种有两个这样的1份，那么，另一种的数量就是前一种数量的2倍。设计二中也有类似的教学环节：“你能画出一个和图3不一样的‘2倍’吗？”相较于设计一，由于少了材料的限制，则显得更加开放与灵动。

诚如波利亚所指出的那样：数学有两个侧面，一方面它是欧几里得式的严谨科学，从这方面看，数学像是一门系统的演绎科学；但另一方面，创造过程中的数学，看起来像是一门实验性的归纳科学。可见，如上教学环节的设计，学生对动手实践活动兴趣更浓，参与热情更高，体会更深刻，学习效果更突出。也充分表明，数学不仅是严谨的演绎，更是创造中的归纳。

四、贴进学生，提升素养

“教学追求被吸引”。好的教学应该具有“战略”性的价值，也就是说，不仅仅要让学生运用已学知识解决一些典型的问题，而且还要力求找寻知识的“附加值”，寻找知识的隐性教学功能，带领学生体会那种登高远眺、“一览众山小”的快感。

促理解进阶。儿童学习概念的初始阶段，或因固有经验中迷思概念的影响，或因概念非本质属性的干扰，常常会出现“依葫芦画瓢”的现象，所以适当的、有意义的训练显得非常重要。两则设计深谙此道。设计一安排了“画一画、比一比”“猜水果”“装球游戏”三道练习；设计二则安排“基础练习”“提高练习”和“挑战练习”三道练习。这些练习有效地体现了基础性、精准性、深刻性与愉悦性等特点。第一是基础性，两则设计的第一题都是基础性练习，帮助学生进一步加深对“倍”的含义的理解。第二是精准性，设计一的第二题“猜水果”让学生围绕两条线索猜“哪一箱是苹果，哪一箱是梨子”，与设计二的第二题中“红气球的个数比黄气球多2个”有异曲同工之妙，都是把两个量之间可能有的“相差关系”和“倍数关系”再次“见面”并加以剖析，使新知的本质特征进一步凸显。第三是深刻性。设计一和设计二的第三题，均糅杂了多个知识点，有着较大的思维空间，激活了学生的思维，使其对“倍”的理解达到再进一个“阶”的水平。

使思想孕育。每个数学知识都兼有事实性、概念性、方法性、价值性四个侧面。知识的事实性指人们在日常生活中对此的感悟和总结；没有概念去概括，客观的事实或现象只能是经验；没有方法去运用，概念或原理只能是词语符号；没有价值取向的揭示，方法只能是机械的步骤，而这种价值取向，更多地聚焦于揭示数学知识背后的灵魂——数学思想。难能可贵，两则教学设计均在事实性、概念性和方法性等方面做足文章的同时，在数学思想的渗透方面也做了一定的尝试。比如，通过多次变化比较双方数值的大小得出倍数，引导学生多次对比，从而明白倍数的含义，有机渗透了抽象的基本思想；围绕大问题，让学生进行自由表征，在多幅作品的对比中，使学生明晰，所谓倍数，就是一个数量包含了几个另一个数量，在“变与不变”的体验中，有机渗透了建模的基本思想；结合观察、表征、填空等环节，在两种数量对比过程中，要求有序摆放，体会上下对齐的优势，有机渗透了“一一对应”的思想等。

当然，课堂教学的追求是无止境的，应该永远是一个“朝向”的姿态。两则教学设计均突出了用“几倍数”去比“一倍数”得出倍数的过程，而“倍”作为一种“度量的数”，似乎还可以反向强化，通过有效地设计，突出“用勺子一次次舀空装满水的容器那样舀”的味道，从不同的侧面强化“倍”的本质，若如此，可能会更有深度和意蕴了。