基于模糊PID的整平机姿态控制算法设计与实现

(江苏师范大学 电气工程及自动化学院，江苏 徐州 221116)

0 引言

整平机是一种通过车辆前端的平地铲水平移动以使地面平整的工程车辆[1]。

目前国内的整平机控制器依赖进口，而我国自主生产的建筑业整平机的整平精度不高[2]，其控制算法一般采用传统的PID。这种控制算法由于控制参数固定不变，在具有高阶非线性特点的整平机姿态控制系统中很难满足控制精度高、响应时间快、抗干扰能力强的要求。

模糊PID控制结合了PID控制鲁棒性强和模糊控制灵活性强的优点，用模糊推理对PID控制参数进行自整定，是一种不依赖模型、稳态精度高、动态性能好的自适应控制算法。本文以整平机平地铲的俯仰姿态控制系统为控制对象，设计了基于模糊PID算法的控制器，通过仿真和实验，验证了其有效性。

1 整平机姿态控制系统和模糊PID原理介绍

1.1 整平机姿态控制系统

整平机姿态控制系统分为俯仰姿态系统和横滚姿态系统，分别调节的是前后水平俯仰角和左右水平横滚角。整平机侧视图如图1所示。

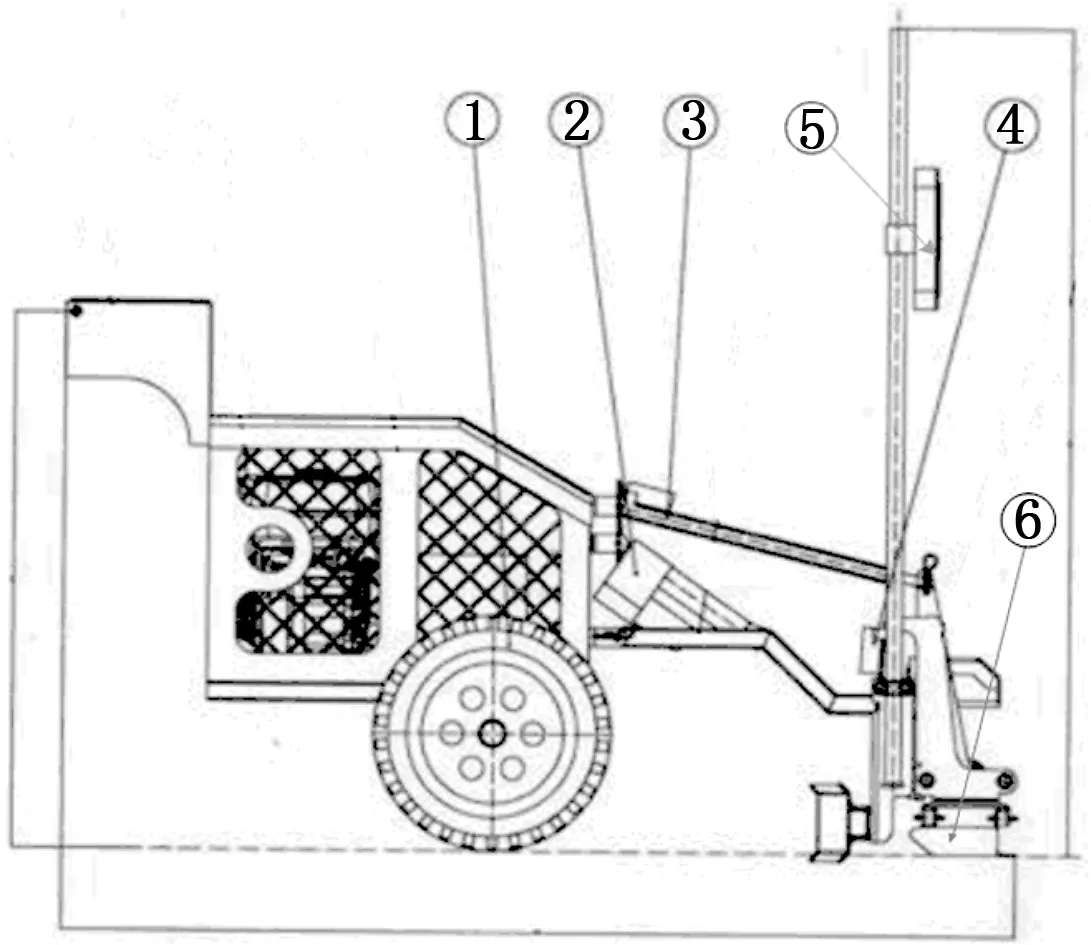
图1 整平机侧视图

图中①为车轮，②为高程调节推杆，③为俯仰角调节推杆，④为横滚角调节推杆(共2个)，⑤为激光接收器，⑥为平地铲。

作业时，通过调节高程推杆，使整平机上的激光接收器接收到由激光发射器发射的激光平面，以达到标高的要求[3]。由于未整平的路面凹凸不平，整平机会带动平地铲发生倾斜，此时控制器会分析平地铲上的传感器采集的数据，经过计算发出合适的控制信号，调整施加在电推杆上的电压，以实现对整平机的姿态控制[4]。随着整平机的行进，时刻保持水平状态的平地铲可完成对路面的整平。

1.2 整平机姿态控制系统实验平台

本文中，整平机姿态控制系统实验平台的传感器采用北微AH300惯性传感器。此传感器选用了高可靠性的加速度计、陀螺仪和磁力计，并使用最优算法确保了所测数据的精确性。它具备数字接口，便于用户集成到系统中，同时其优秀的制造工艺确保了传感器在各种整平环境下都能正常运行。

系统的处理器采用STM32F407。它是基于ARM®的CortexTM-M4为内核的STM32F4系列高性能微处理器。拥有集成度高、数据传送速度快、外设扩展性强、接口支持多样性强等特点，满足了整平机姿态控制系统对处理器的要求。

系统的执行元件为额定电压24 V的电推杆，其中包括了横滚角调节电推杆、俯仰角调节电推杆和模拟路况电推杆[5]。整平机实验平台整体图如图2所示。

图2 整平机实验平台

惯性传感器将实时采集的角度信号通过RS232传输给处理器STM32F407。控制器分析处理角度值，根据设定的控制算法，发送控制信号对各电推杆的PWM驱动电路进行控制，进而实现对平地铲的水平姿态控制。

1.3 模糊PID原理

常规位置式PID算法表示为：

(1)

式中，u为系统输入量；KP为比例系数，KI为积分系数，KD为微分系数；e为期望值与测量值的误差；ec为误差变化，即：

ec(k)=e(k)-e(k-1)

(2)

模糊控制是一种经验规则控制策略，由语言变量和模糊集合组成。模糊控制器包含四部分：模糊化、模糊规则库、模糊推理和解模糊[6]。

模糊PID是一种用模糊推理的方法分别对PID控制参数进行在线自整定的自适应控制算法。其结构如图3所示，通过计算当前系统误差e和误差变化ec，利用模糊规则进行模糊推理，对PID的比例、积分、微分3个控制参数进行在线整定，以满足不同的e和ec对控制参数的不同要求。模糊PID的运用使控制器既具有模糊控制适应性、灵活性强的优点，又具有PID控制容错性、鲁棒性强的优点，使被控对象拥有良好的动态、稳态性能。

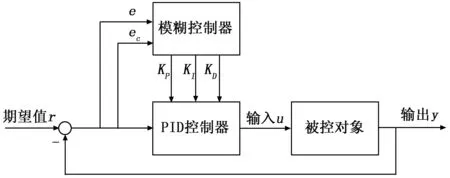
图3 模糊PID结构

2 控制器参数设计和算法仿真

2.1 输入输出变量的模糊化及隶属度函数

模糊控制器的输入为惯性传感器所测的俯仰角与期望值(一般为0°)的误差e及误差变化ec，输出为比例系数KP、积分系数KI和微分系数KD。

设定以上5个变量对应的模糊语言变量的模糊论域均为 {NB，NM，NS，ZO，PS，PM，PB}，分别代表负大、负中、负小、零、正小、正中、正大[7]。

整平机姿态控制系统中俯仰角变化的最大幅度约为±9°，期望角度值为0°，所以在模糊PID控制算法中，e的取值范围为 [-9，9]。以e的模糊化为例，[-9，-6]属于NB，[-9，-3]属于NM，[-6，0]属于NS，[-3，3]属于ZO，[0，6]属于PS，[3，9]属于PM，[6，9]属于PB。本系统中，系统采样间隔为50 ms，在一个采样间隔中误差变化ec的取值范围为[-0.18，0.18]。

由现场经验可以得出，KP、KI、KD的取值范围分别为[0，6000]、[0，120]、[0，6]，由于KP、KI、KD的取值不为负，模糊论域的名称仅供划分区间使用，不代表各参数本身的正负值。以KP的模糊化为例，[0,1000]属于NB，[0，2000]属于NM，[1000，3000]属于NS，[2000，4000]属于ZO，[3000，5000]属于PS，[4000，6000]属于PM，[5000，6000]属于PB。

隶属度函数一般分为三角形、梯形、高斯形等。为了计算简便，本文采用三角形隶属度函数。设e、ec的隶属度变化范围为[-3，3]，KP、KI、KD的隶属度变化范围为[0，6]，则量化因子Ke=3/9=1/3，Kec=3/0.18=50/3，KKP=6000/6=1000，KKI=120/6=20，KKD=6/6=1。

2.2 模糊规则和模糊推理设计

设置模糊规则是实现模糊PID控制的关键，需要大量的先验理论和工程经验。如果没有完整深入地了解系统的运行规律，建立的模糊规则表将无法使控制效果达到最优，甚至比常规PID控制还要差，无法满足系统性能需求。

对于整平机姿态控制系统，e和ec变化时，相对应最优的KP、KI、KD应当按照如下规律去整定：

(1)当|e|很大时，为了加快响应速度，无论ec大小如何，都应取较大的KP以迅速减小误差。为了防止积分饱和导致严重超调，误差较大时不使用积分控制，KI取0。同时为了避免KD削弱响应速度，KD此时也取0。

(2)当|e|中等大小时，为了保证响应速度并避免超调过大，应适当减小KP，适当增大Ki和Kd。其中，当ec和e的符号相同时，角度值正远离期望值，此时取较大的KP；当ec与e的符号相反时，角度值正靠近期望值，此时取较小的KP。

(3)当|e|很小时，为了防止振荡、超调，继续减小KP、增大KD。为了保持积分项消除稳态误差的作用，KI也要增大。为了使角度值稳定在期望值附近，当|ec|较大时，KD取较小值，当|ec|较小时，KD取较大值。此时可保证系统拥有较好的稳态特性[8]。

模糊推理需要查询模糊规则表，根据输入量的隶属度计算求出每个输出量对应的隶属度。

根据合成运算法则的不同，模糊推理方法包括Mamdani取小推理法、Larsen乘积推理法、Zadeh运算法和布尔运算法等。

Mamdani取小推理法是最简单的模糊推理法，使用也最为广泛。可通过取模糊集合输入量A、B中较小的隶属度作为输出量C的隶属度。Larsen乘积推理法和Mamdani取小推理法唯一区别是在合成输出量隶属度时，前者使用了乘积而非取小运算。Larsen乘积推理法计算简单，并且不同于Mamdani取小推理法丢失了一个隶属度的信息，所以本系统的模糊推理采用Larsen乘积推理法。

Larsen乘积推理法公式如下：

(3)

式中，μa(ui)和μb(vi)分别为输入量A集合中ui以及B集合中vi的隶属度，μc(zi)为输出量C集合中zi的隶属度。

任意一组e和ec都有2个不小于零的隶属度，通过查询模糊规则表，可得到表格中对应的4组输出模糊量，运用Larsen乘积推理法即可分别求出每个输出模糊量对应的隶属度，其中对应同一个模糊量的隶属度采用相加合成。

2.3 解模糊

模糊推理所得出的KP、KI、KD的输出量为模糊量，无法作为实际控制量。此时需要运用特殊方法分析输出模糊量及其隶属度，并计算出精确的输出值，此过程即为解模糊。

解模糊法包括最大隶属度法、重心法、加权平均法等。为了获得更准确的控制量，充分利用已有信息，本文采用重心法进行解模糊。重心法的一般表达式为：

(4)

式中，z0为模糊量解模糊之后的精确值；zi为论域内的模糊值；μc(zi)为zi的隶属度。

2.4 Matlab/Simulink仿真

本文的仿真模型采用混凝土激光整平机俯仰角控制机构模型[9]，该模型利用刚体转动和平动原理进行机理建模。

结合控制参数整定规律，并经过多次实验反复优化，可得到模糊规则表，如表1所示。

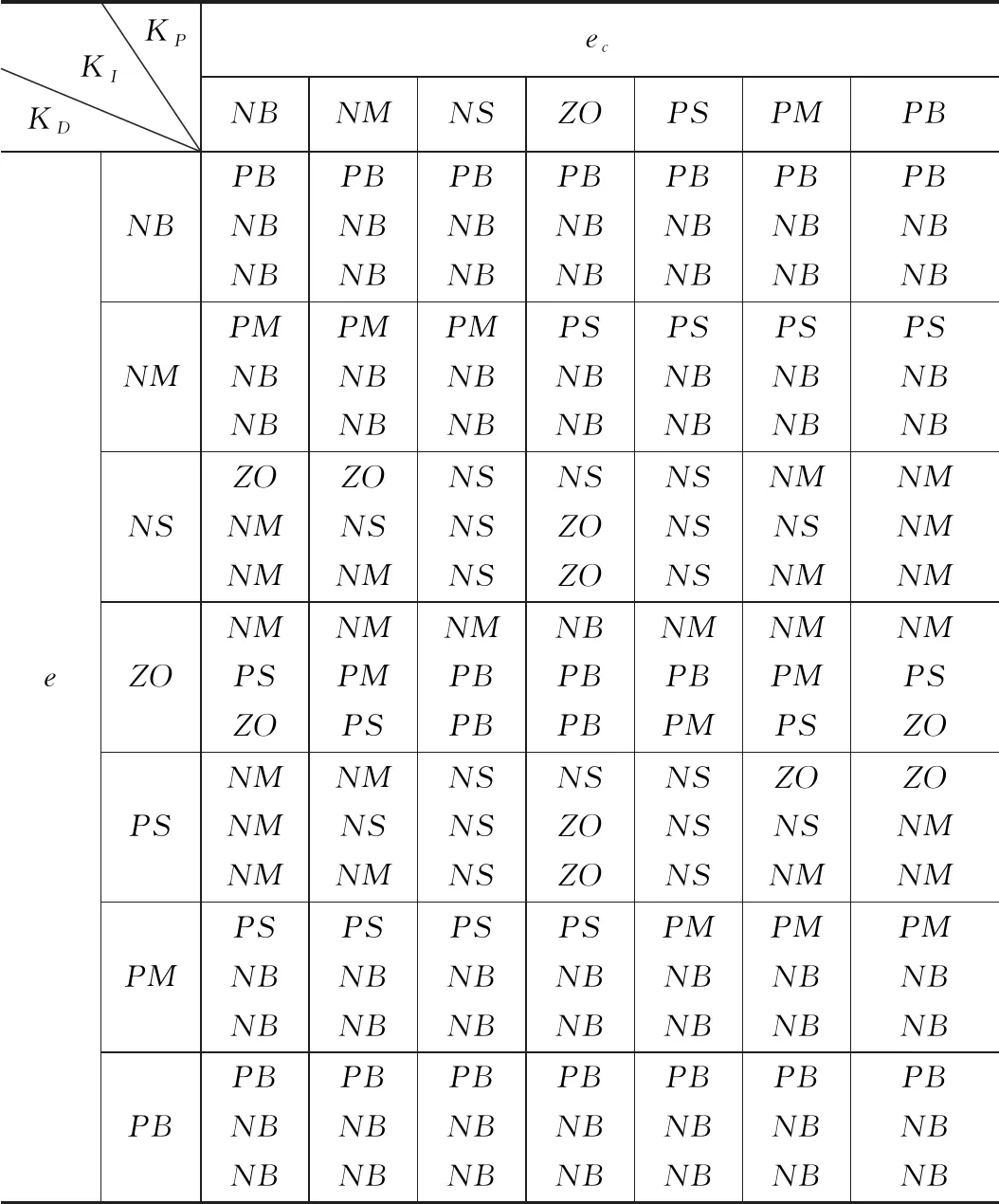
表1 模糊规则表

整平机俯仰姿态控制仿真的初始俯仰角设置为8°。分别记录常规PID和模糊PID控制下俯仰角调整到期望值0°的过程，绘制的仿真结果如图4所示。

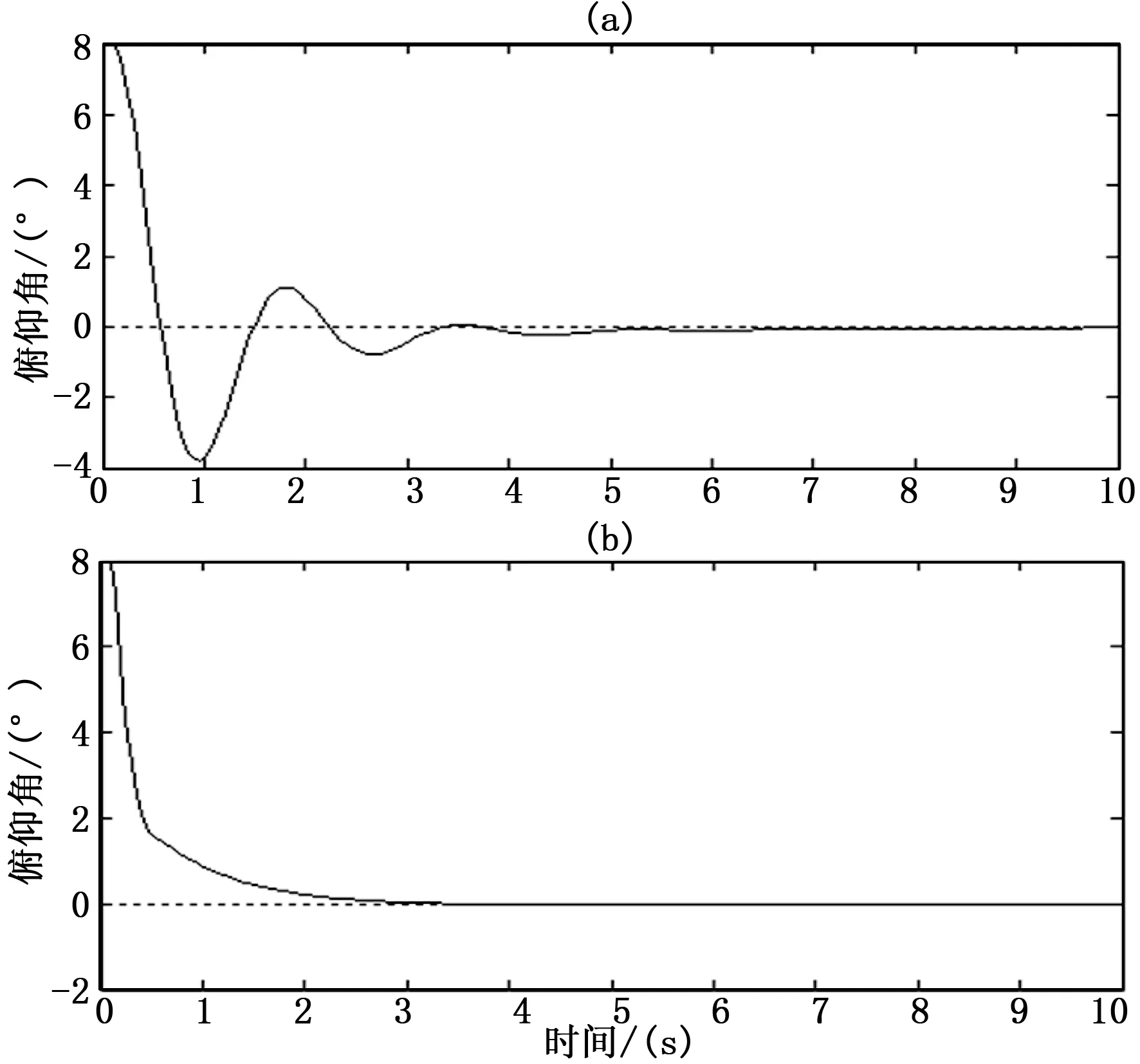
图4 PID与模糊PID控制效果仿真对比图

图中：(a)为施加常规PID控制时的俯仰角变化，(b)为施加模糊PID控制时的俯仰角变化。

2.5 仿真结果分析

分析图(a)可知，常规PID易产生超调和震荡，且俯仰角从8°调整到0°并稳定需要7 s的响应时间。

分析图(b)可知，模糊PID除了保留常规PID无静差特性之外，有着更快的响应速度，俯仰角从8°调整到0°并稳定只需要4 s，且没有超调和震荡。

综上，模糊PID由于其控制参数自整定的特性，与控制参数固定的常规PID相比，保持了高控制精度，并有着更快的响应速度。

3 算法软件设计

软件设计思路和编程方法：

基于模糊PID的整平机姿态控制系统采用处理器STM32F407进行通信和运算，软件开发环境为MDK5,编程语言为C语言。

软件程序由主程序、角度采集及解算子程序、模糊PID控制算法子程序、PWM波输出子程序、显示子程序组成[10]。软件流程图如图5所示。

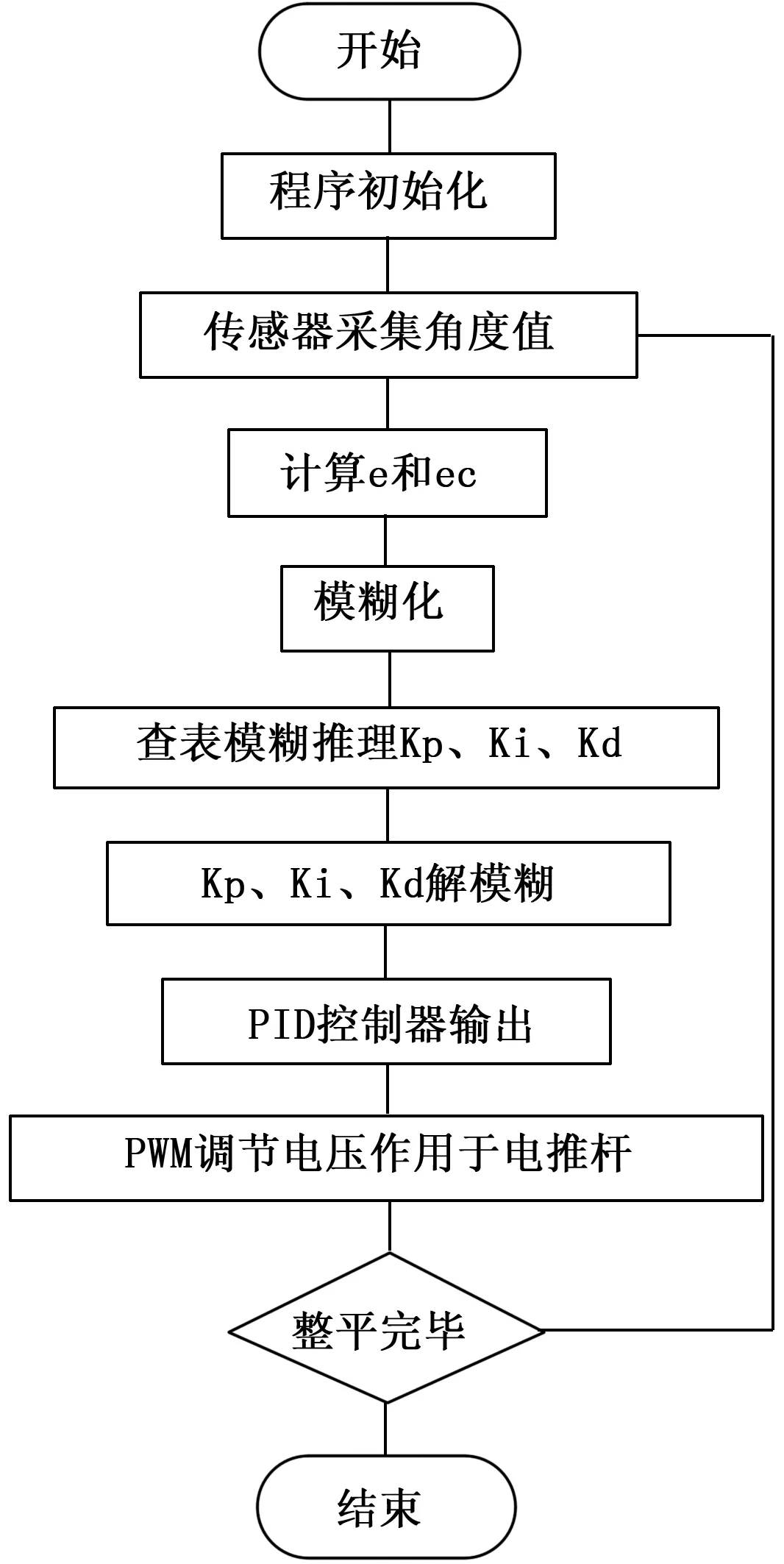
图5 整平机姿态控制软件算法流程图

4 实验结果与分析

4.1 实验步骤和方法

本次实验对象为整平机实验平台的俯仰控制系统。为了模拟整平机作业时路面的复杂情况以验证模糊PID控制抗扰动的能力，实验中对影响俯仰角的模拟路况电推杆额外增加了9 V的周期方波电压作为干扰。

在模拟路况的电压干扰下，分别对比了常规PID和模糊PID对整平机实验平台的俯仰姿态系统的控制效果。

4.2 实验结果图

本次实验采样间隔为50 ms，采样时间为25 s。采集数据后绘制的控制效果对比图如图6所示。

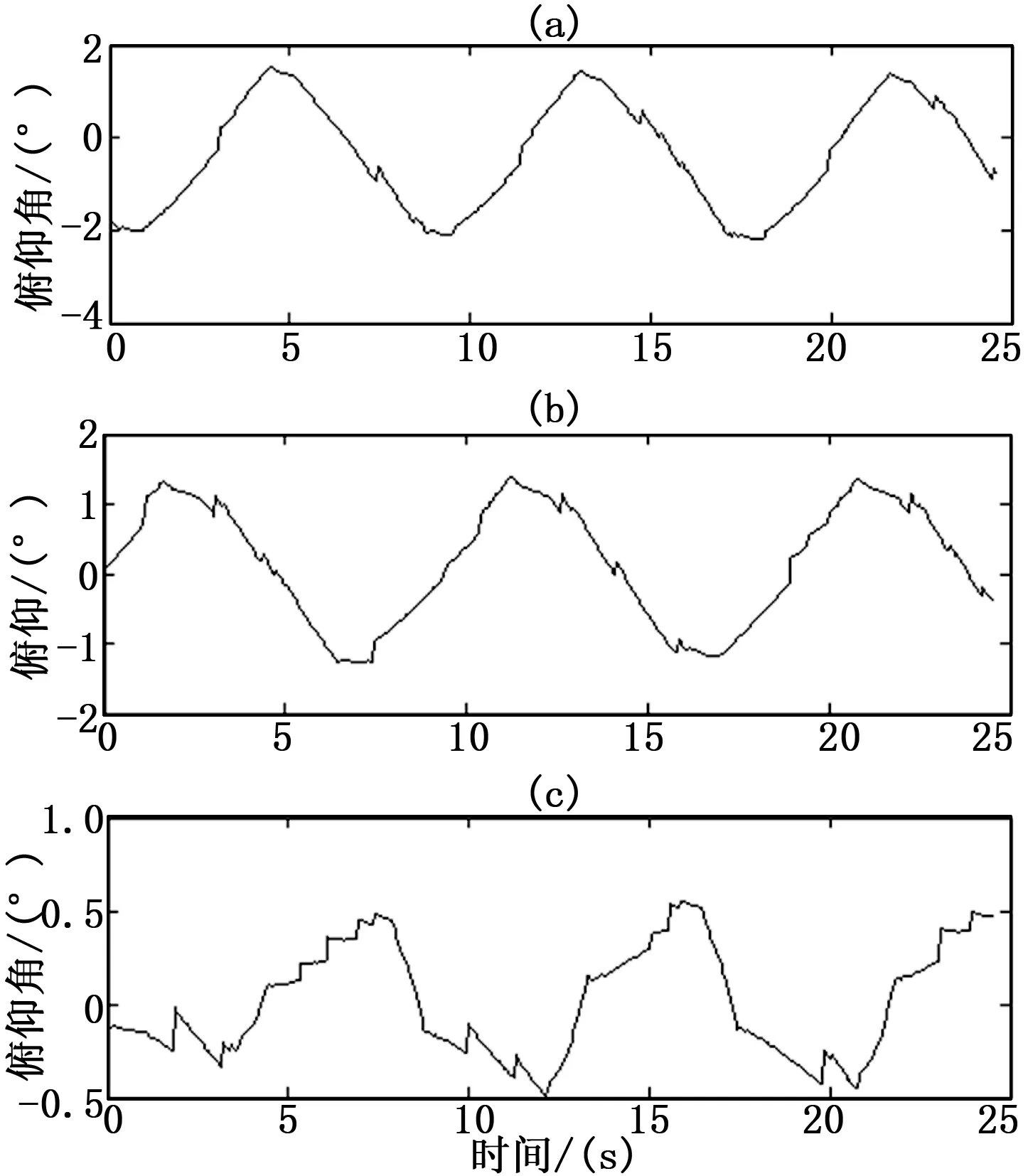
图6 模拟路况扰动下PID和模糊PID控制效果对比图

图中：(a)为模拟路况干扰下，不施加控制时的俯仰角变化，(b)为模拟路况干扰下，施加常规PID控制时俯仰角变化，(c)为模拟路况干扰下，施加模糊PID控制时俯仰角变化。

4.3 实验结果分析

分析图(a)可知，控制器不作用时，模拟路况的干扰使整平机俯仰角产生了±2°的波动。

分析图(b)可知，系统增加了常规PID控制后，通过整定3个控制参数，俯仰角的变化范围最多缩小至±1.3°，常规PID虽然有一定的抵抗扰动的功能，但俯仰角变化范围依然达到了2.6°。

分析图(c)可知，将控制算法换成模糊PID后，在模拟路况的扰动下，系统虽然受扰动的影响，但俯仰角的变化范围可控制在±0.5°之内。通过模糊PID控制，系统的抗干扰能力显著增加了，整平精度较常规PID控制有了大幅提升。

5 结束语

本文设计并实现了基于模糊PID的整平机姿态控制算法，仿真和实验结果表明，模糊PID控制算法可以将整平机姿态角回归水平的时间缩短在4 s内；同时可以在路况扰动剧烈的情况下，使姿态角稳定在±0.5°之内。该算法提升了整平机姿态控制系统的整平精度、响应速度及抗干扰能力，为理论研究和工程应用提供了重要价值。