转移概率部分未知时滞跳变系统有限时间H∞控制
2019-07-25
(江南大学 轻工过程先进控制教育部重点实验室, 江苏 无锡 214122)
0 引言
由于环境的突变,子系统间跳变等随机突变因素的影响,传统切换系统很难描述上述随机跳变模型,为了减弱上述随机突变对系统的影响,可以用马尔科夫跳变系统模型来精确表示此类存在突变的数学模型。马尔科夫跳变系统具有广泛的应用背景,该系统有两部分构成, 一部分是用离散时间或连续时间动力学模型来描述的子系统, 另一部分是马尔科夫链, 子系统的状态轨迹沿着此链在各个时间区间内进行随机的跳变。在电力系统、通讯系统、制造业系统等[1]方面马尔科夫跳变系统彰显了强大的建模能力。近年来,马尔科夫跳变系统已成为控制理论界热门的研究方向之一,主要包括稳定性与控制器设计[2-5],系统故障检测与容错控制[3,6],滤波及状态估计[3,7,8]。
跳跃过程中转移概率很大程度上决定了系统的性能, 但是获取精确的转移概率是非常困难的,在考虑转移概率部分未知的条件下,已有大量文献对其进行了研究[9-12]。文献[10]针对转移概率部分未知的马尔科夫跳变系统鲁棒控制问题[10]进行了研究。文献[11]研究了马尔科夫跳变系统的稳定性。文献[12]在转移概率部分未知,执行器和传感器同时故障的条件下,通过对系统故障同时估计方法,设计了系统观测器和控制器。在很多实际工业系统中,由于信号在传输过程中存在时延和测量不灵敏等因素,时滞对于系统来说是不可避免存在的,也是导致控制系统不稳定的因素之一。因此对于具有时滞,状态转移不确定的跳变系统的稳定性分析具有重要意义并且也取得了很多成果[13-18]。
近几年来,有限时间控制在工程实践中的应用越来越广泛,而现有文献主要研究无限时域内的李雅普诺夫渐进稳定性问题,对于许多工业应用系统,诸如飞行器的姿态控制、化学反应的温度控制、导弹跟踪控制而言,我们更加关注的是动力系统在固定有限时间间隔上的行为即某段时间系统的特性,例如,当系统的控制回路存在饱和元件或者控制飞行器在一个特定时间区域内从一个点转移到另一个点的轨迹问题时,都会遇到系统的有限时间稳定问题。而有限时间稳定性则可以很好的对此进行衡量。近几年对于有限时间稳定性控制问题引起了广泛关注[19-25]。
受以上分析启发,本文讨论了在转移概率部分未知情况下的时滞马尔可夫跳变系统基于观测器的有限时间控制问题。主要目的是设计一种状态观测器和状态反馈控制器,保证闭环系统随机有限时间的稳定性。主要分为以下三个部分来说明:1) 对于时滞马尔科夫跳变系统进行有限时间稳定性分析,考虑状态转移概率矩阵部分未知情况, 相较于基于精确状态转移概率矩阵的文献更具实用性; 2)在进行系统控制器和观测器设计时,由于分析过程中所得的线性矩阵不等式具有非线性项,使用解耦技术来解决,得到一组可以求解的线性矩阵不等式;3)通过求解得到的观测器增益和控制器增益矩阵,进行SIMULINK仿真,验证所提方法的有效性。
1 系统描述及准备工作
考虑如下的时滞时序马尔科夫跳变系统:
(1)
其中:x(t)∈Rn、u(t)∈Rm、y(t)∈Rρ、z(t)∈Rρ分别是系统的状态向量,控制输入,测量输出和被控输出,τ是系统的时滞常数,f(t)∈Rt系统时变不确定的有界未知输入信号,包括扰动、噪声等,不失一般性。{rt,t≥0}是在有限集合R={1,2,...,N}中随时间t取值一个马尔科夫随机过程,rt表示系统跳变模态,转移概率矩阵定义为Γ={πij},i,j∈R,由t时刻的模态i转移到t+Δt时刻的模态转移概率为:
(2)

假设外部扰动满足:
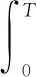
(3)
本文考虑转移概率部分未知情况,如某个含4个子系统的马尔科夫跳变系统可能具有如下转移概率:
(4)

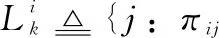

(5)
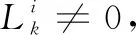
(6)
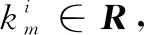
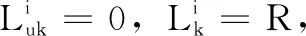
对于系统(1)选取如下的时滞状态观测器和反馈控制器:
(7)
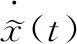
(8)
其中:
本文的任务主要是在保证闭环系统在有限时间稳定的情况下,设计系统(8)的H∞控制器和观测器,使得系统满足一定的性能指标要求。同时,以LMI的形式给出H∞控制率的存在条件以及观测器和控制器增益的求解方法。
在分析前给出以下定义和引理:
定义1 (有限时间稳定性) 对于时滞跳变系统(1),给定三个正常数σ,ε,T满足0<σ<ε,,和一组正定矩阵R(rt),若对于∀t1∈[-τ,0]和∀t2∈[0,T].如下式子成立:
xT(t1)R(rt)x(t1)≤c1⟹xT(t2)R(rt)x(t2)≤c2
(9)
则系统(1)是关于σ,ε,T,R(rt),d有限时间镇定的。
定义2 (有限时间H∞稳定性) 对于闭环系统(8),给定三个正常数σ,ε,T满足0<σ<ε,T>0和一组正定矩阵R(rt),对于∀t∈[0,T],若存在一个正常数γ>0,若增广系统满足如下要求:
(1)当外部扰动满足(3)时,增广跳变系统(8)有限时间镇定。
(2)在零初始状态下,跳变系统(8)控制输出z(t)满足:
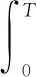
(10)
则闭环系统(8)是关于σ,ε,T,R(rt),d,H∞有限时间有界的。
(1)A<0,D-CA-1B<0;
(2)D<0,A-BD-1C<0.
2 有限时间稳定性分析
在这一小节中主要对系统进行有限时间稳定性分析,给出了闭环系统(8)有限时间稳定的充分条件,并进行证明。

(11)
(12)
(13)
(14)
其中:
证明 构造如下的李雅普洛夫函数:
(15)
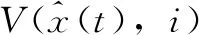
(16)
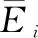
(17)

(18)
对于∀t∈[0T],对上式(18)从0到T进行积分,可以得到如下不等式成立:
(19)
从式子(19),可以看出:
(20)

从而:
(21)


(22)
证明 在零初始条件下,对于增广系统(8),选取李雅普诺夫函数:
根据Schur定理,式子(22)可以等价于:
(23)
由于:
(24)
可以看出:
(25)
系统(8)是有限时间镇定的。此外对于系统(8),根据不等式(12) (13) (22)可以得到:
(26)
上式两边同时乘以e-αT,可以得到:
(27)
在零初始条件下,对上式积分可得:
(28)
由上式可得:
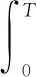
(29)
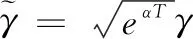
从定理1可知,对于上文选取的合适的李亚普洛夫函数,不等式(11)(12)(13)(14)保证了闭环系统(8)有限时间稳定性。若在不考虑干扰的情况下,不等式(22)就退化成不等式(11),进一步说明,满足定理2的控制器和观测器不仅满足一定的H∞性能指标,也能保证系统有限时间的稳定性。
由于定理2存在非线性乘积耦合项,这就需要在前文假设的条件下,在进行观测器和控制器设计时,应用引理,得到消去非线性项的线性矩阵不等式。
3 系统控制器和观测器设计
上一小节给出了系统有限时间稳定的充分条件,但所提出的线性矩阵不等式存在非线性项,这一小节中对于耦合项进行处理,进行系统控制器和观测器设计,得到一组可以求解控制器增益和观测器增益的线性矩阵不等式。

(30)
(31)
(32)
(33)
(34)
0 (35) (36) 其中: W1i=-diag{Xk1i…Xkr-1i,Xkr + 1i…Xkmi} 系统的状态反馈控制器增益为Ki=YiXi-1。 (37) 其中: θ11=AiTPi+PiAi+KiTBiTPi+PiBiKi+ θ12=-PiBiKi,θ13=PiAdi+PiBiKdi,θ14=-PiBiKdi, θ22=AiTPi+PiAi-CyiTHiTPi-PiHiCyi (38) 注意到,θ22和θ24是非线性的,存在乘积耦合项Pi和Hi都是需要待求的矩阵,这里定义系统观测器增益矩阵Hi=Pi-1CyiT,则θ22和θ24等价于: θ24=PiAdi-CyiTCydi XiXj-1Xi-Li< 0j∈Luki,j≠i,(40) (41) 上式(40)(41)分别等价于(32)(33)。 另一方面,定义: (42) 从条件(34)和(35),可以得到: 将上面条件带入式子(42),则可得不等式(36),证毕。 对于四模态的时滞马尔科夫跳变系统(1),其系统参数为: 模型1: Cd1=[-0.1 0.1],D1=[0.5],Cyd1=[0.1 -0.2]. 模型2: Cd2=[0.3 0.2],D2=[0.2],Cy2=[0.2 -1],. 模型3: Cd3=[0.3 0.5],D3=[0.3],Cy3=[0.2 -2],. 模型4: Cd4=[1 2],D4=[0.4],Cy4=[0.2 -1],. 针对上述系统进行有限时间稳定性分析,控制器和观测器设计。 选取系统参数c1=0.25;α=1.0;d=1;T=2;Ri=I;τ=0.5。 假设系统的转移概率矩阵为: 其中: ?为系统转移概率未知部分,运用Matlab的LIM工具箱,求解线性矩阵不等式,可以得到系统状态控制器增益和状态观测器增益如下: K1=[-3.1629 -5.5160],K2=[-3.0890 -5.6813] K3=[-1.1179 -2.7311],K4=[-3.3143 -4.0815] Kd1=[-0.1133 0.1301],Kd2=[0.0108 -0.312] Kd3=[-0.1167 0.1491],Kd4=[0.0491 -0.3328] H1=[1.0551 1.0065]T,H2=[2.9854 -3.4310]T, H3=[1.9238 1.4342]T,H4=[5.0045 -5.7889]T. 对于上述算出的控制器增益和观测器增益,使用SIMULINK仿真,选取系统噪声为方差0.01的白噪声,仿真时间为2秒,延时为0.5秒,系统初始状态值为[2 -9]T,则可以得到系统的模态转化图,和状态响应仿真图。 图1 仿真图 从仿真图形中可以看出,对于具有转移概率部分未知的时滞跳变系统,所设计的控制器和观测器仍然可以保证系统(1)有限时间H∞稳定,证明了所设计的状态反馈控制器和观测器是有效的。 本文研究了在一定性能指标约束条件下,转移概率部分未知时滞马尔科夫跳变系统有限时间H∞控制问题,通过扩展跳变系统状态,将系统转换为具有跳变参数的广义描述系统,针对此系统进行控制器设计,保证系统有限时间稳定性。采用自由加权矩阵法, 处理转移概率部分未知情况,保证所得线性矩阵不等式条件具有更小的保守性。最后,通过SIMULINK仿真验证了所提算法的有效性。值得注意的是,本文中考虑的是确定时滞对系统的影响,针对于时变时滞情况,这是后续需要研究的内容。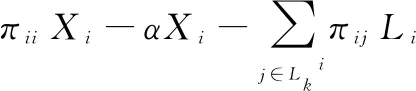
4 实验结果与分析
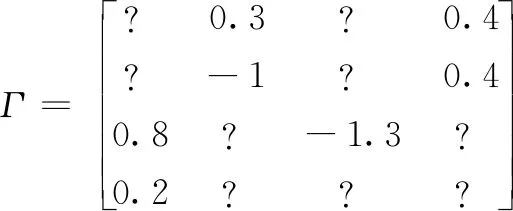
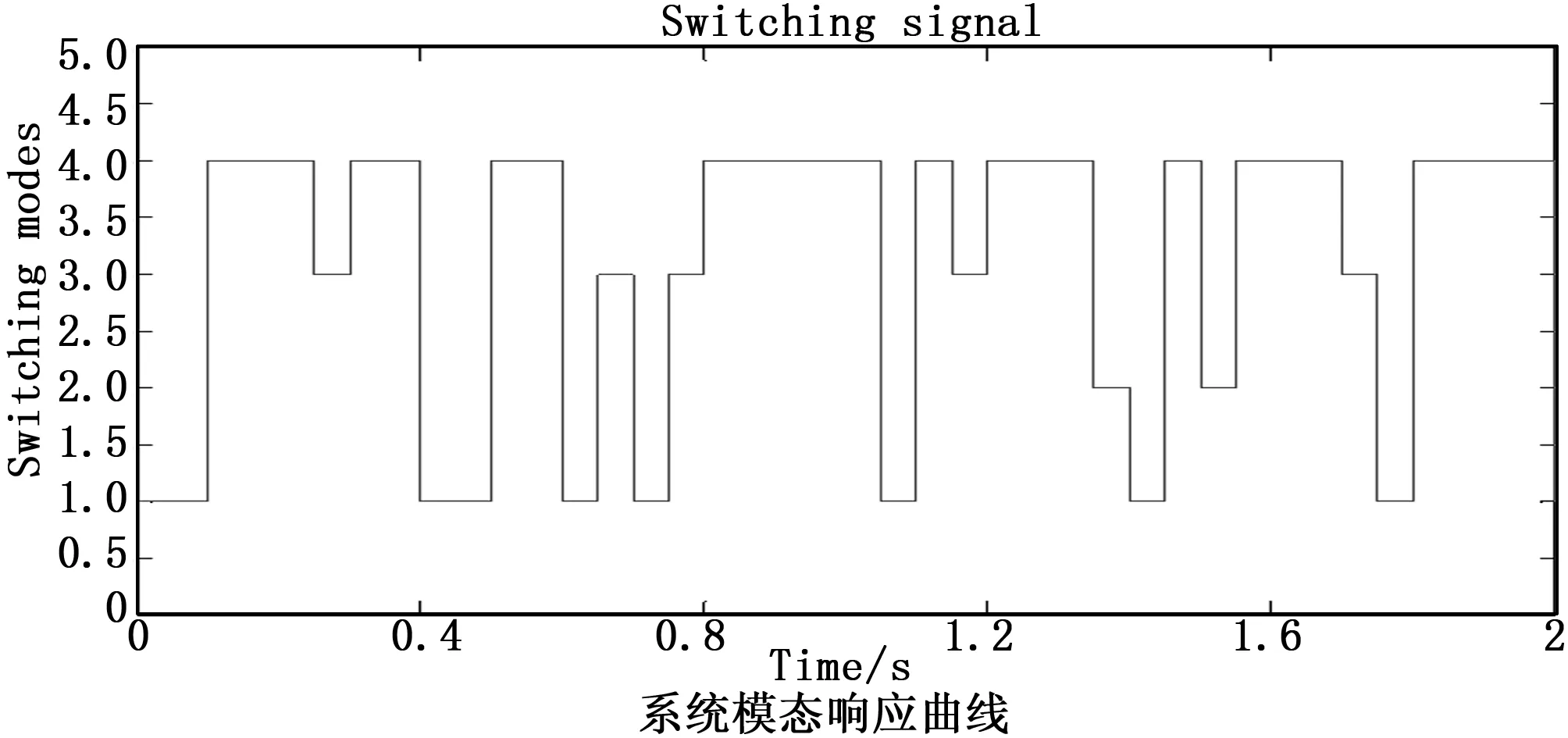
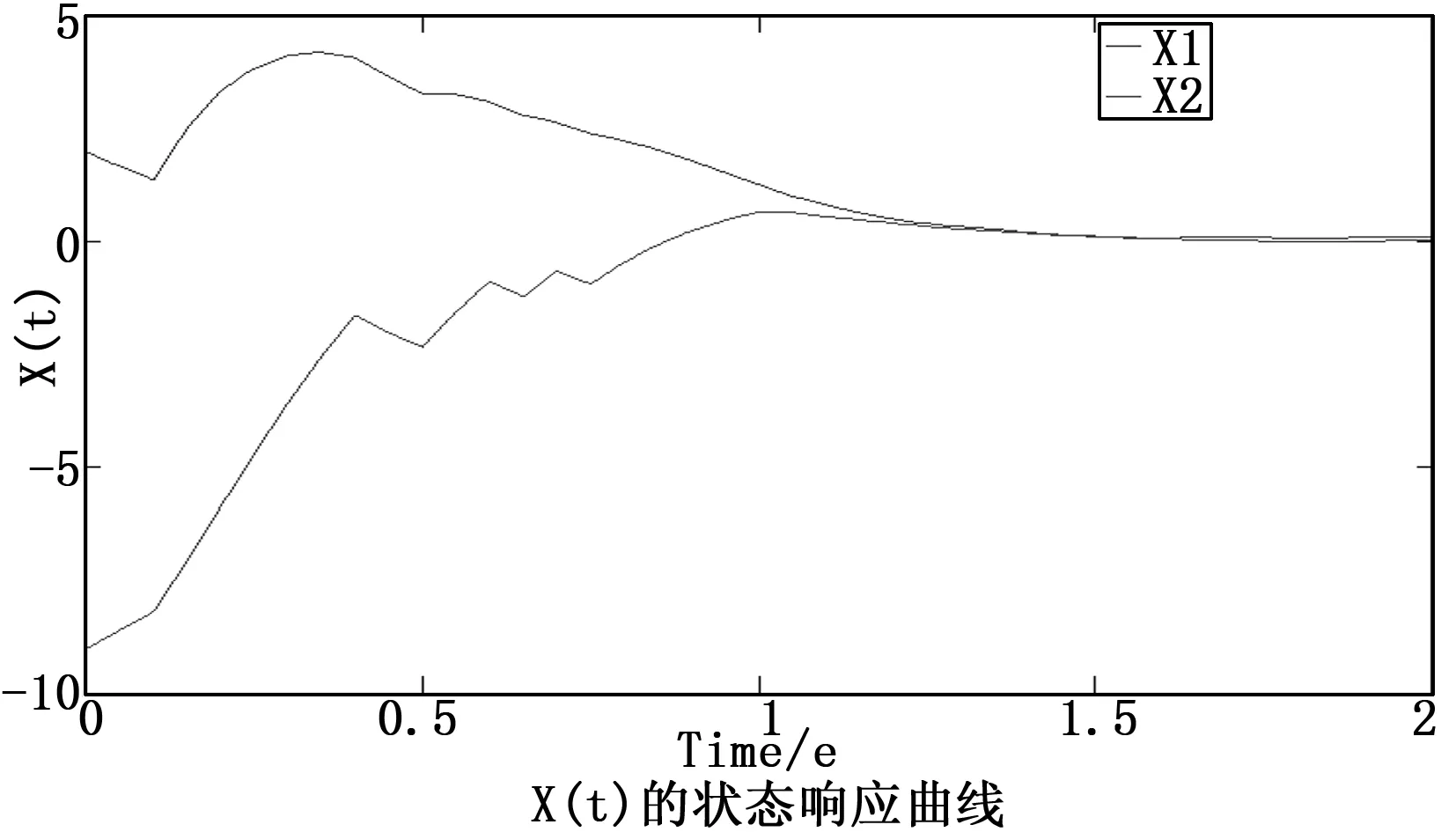
5 结束语
