水文序列相依变异识别的RIC定阶准则——以自回归模型为例

李雅晴，谢 平，2，桑燕芳，陈 杰，赵羽西，吴林倩

（1. 武汉大学水资源与水电工程科学国家重点实验室，湖北武汉 430072；2. 国家领土主权与海洋权益协同创新中心，湖北武汉 430072；3. 中国科学院地理科学与资源研究所陆地水循环与地表过程重点实验室，北京 100101；4. 国家电网公司西南分部，四川成都 610000）

1 研究背景

水文时间序列分析是揭示和认识水文过程变化特性的有效手段和重要途径［1］。随着全球气候变化和人类活动影响的加剧，流域下垫面条件和水文过程的时空分配均受到显著影响，用于水文分析计算的水文序列不再满足一致性条件［2-4］。水文学上将这种水文序列的统计规律（包括分布形式和分布参数）在整个研究时间范围内发生显著变化的现象称作水文变异［5］，其包括跳跃、趋势、周期和相依等多种变异形式［6］。

国内外大量观测资料分析计算显示，许多河流的年径流序列存在相依性［7-8］，即发生了相依变异，表现为序列后一数据与紧邻的前一（几）数据具有成因、数值等方面的继承性。水文过程的相依性会影响一系列水文分析计算工作。实际中，研究径流序列相依性有助于分析流域植被覆盖［9］、特殊生态环境［10］的影响；计算水库多年调节库容时需考虑年径流的相依性以避免计算结果偏小［11］；水文过程预测也需要考虑序列的相依性以保证预测结果的合理性［12-13］。利用随机水文学的方法对跳跃、趋势和周期等确定性成分进行识别和分离后，若剩余序列不包含相依变异成分（即只含纯随机成分），因而满足一致性计算条件，可使用统计水文方法进行研究，例如水文频率计算；若剩余序列含有相依变异成分，需利用回归滑动模型进行研究［14］。

AR模型（即自回归模型）是描述时间序列相依性的数学模型。自Maass［15］以及Yevjevich［16］将AR模型用于河流流量预报后，被广泛用于水文水资源时间序列分析中。建立AR模型的过程包括确定模型阶数、估计参数以及模型检验等。通常在掌握大量观测数据并进行预处理后，需从样本数据中估计模型参数，主要方法有矩估计（Yule-Walker方程）、最大似然估计和最小二乘估计等。关于模型定阶的方法主要分为两种途径：（1）利用时间序列的自相关性，依据自相关系数和偏相关系数的拖尾或截尾初步确定其阶数，或采用奇异值分解（SVD）法、LD递推法、Gram-Schmidt正交法等方法，但这些方法在计算时间和精度上难以两全［17］；（2）用模型拟合残差或预测误差作为定阶依据，主要有F-检验、FPE（Final Prediction Error）准则、AIC准则（Akaike Information Criterion）、BIC准则（Bayesian Infor⁃mation Criterion）等。其中，F-检验因存在人为选择置信度，具有一定的主观性；FPE 准则仅适用于AR 模型定阶［18］；AIC 准则对于小样本问题往往会选择较为复杂的模型，并且惩罚度较低［19］；BIC 准则在小样本定阶时准确率往往会受到影响［20］。此外，上述准则只具备定阶功能，关于模型检验通常还需采用综合自相关系数检验法或自相关分析法对拟合残差εt进行独立性检验，若εt是独立的，则模型满足要求。

由于水文序列的相关系数可以表示序列的相依变异程度［21］，而相关系数的均方误σr可用于表示样本相关系数的可靠性［22］，以及原始序列与相依变异成分的拟合误差。此外，信息熵是研究水文水资源科学领域不确定性的有效工具，以信息熵理论为基础可分析降雨-径流关系［23］，揭示降水时空分布特征［24］，估计线性模型参数［25］等。其中，徐南荣等［26］提出基于信息熵的相关熵概念作为度量随机变量与序列整体相关关系的指标，用于自回归滑动平均模型（ARMA）的参数估计；曾金芳等［27］依据信息熵提出了一种曲线拟合辨识方法并验证了其适应性。

本文依据相关系数可以度量相依成分的变异程度以及信息熵理论对序列不确定性的度量，提出一种水文序列相依变异的RIC定阶准则（R表示相关系数，IC表示Information Criterion）。该准则的优点是在定阶的同时可进行相依程度分级与独立性检验。通过公式推导说明该准则的理论依据，以一至四阶自回归模型为例，通过统计试验以验证RIC准则的可行性，并与AIC、BIC准则的定阶准确率进行比较，最后利用实测序列进行分析验证，说明RIC准则的适应性与定阶结果的合理性。

2 常用定阶准则

2.1 AIC 准则AIC 准则也称为最小信息准则，由日本统计学家Akaike 于1973 年提出，是用于AR模型的定阶理论［28］。随后推广到判断ARMA模型的阶数，并引申到时间序列混合回归模型。AIC准则是极大似然法和信息理论的结合，其中信息理论表现在Kullback-Leibler 相对熵的运用，以对数似然比表示。当模型用p个独立参数来拟合数据时，其一般形式为：

对于AR模型，在最小二乘法估计误差的情况下，AIC准则的函数式可以写为［29］：

由式（2）可见，AIC准则函数由两项构成，第一项为拟合误差量，体现模型拟合的好坏，它随着阶数的增大而减小；第二项标志了参数数目，因为参数过多意味着模型不确定性增加，因此视为惩罚项，随着阶数的增大而增大。这两项的综合使用使得AIC准则函数值达到最小时的p值即为模型的理想阶数。AIC准则虽然为时序模型定阶带来了许多方便，但已有理论证明AIC准则不能给出相容估计，并且一般所得模型阶数总高于真值［30-31］。

2.2 BIC准则当样本序列长度n →∞时，采用AIC准则确定的模型阶数估计值并不能依概率收敛到真实值上，为了得到相容估计，Akaike［32］和Schwarz［33］等在AIC准则的基础上根据贝叶斯原理提出了BIC准则。BIC准则函数的定义如下所示：

与AIC准则相比，式（3）右边的第二项lnn 代替了式（2）中对应的系数2，仍由两部分构成。一般情况下lnn ＞＞2，因此对于同一序列进行拟合时，AIC准则达到极小值时所对应的阶数往往比BIC准则所定的阶数要高。

3 RIC准则原理

研究水文序列的相依变异特性时，需要首先判断并去除水文序列中的确定性成分，然后通过序列独立性检验判断剩余成分中是否含有相依成分，对含有相依成分的序列除了建立合适的拟合模型外，还需要对相依程度进行判断。AIC准则与BIC准则虽然均能确定模型的阶数用以建模，但不能判断模拟序列相依变异的程度，也不能检验（残差）序列的独立性。为克服这些准则存在的局限性，本文提出针对水文相依变异识别更为完善的RIC准则。

采用适当方法去除跳跃、趋势和周期等确定性成分后，若剩余序列xt中含有相依成分，可以采用自回归模型AR（p）模型进行描述：

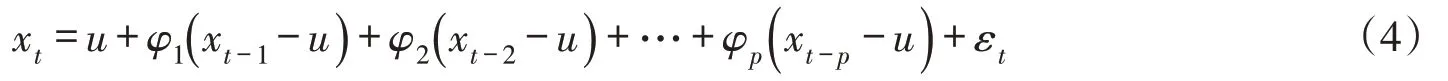
式中：u为xt的均值；φ1，φ2，…，φp为自回归系数；p为自回归阶数；εt为均值0、方差的独立纯随机变量，且与xt-1，xt-2，…，xt-p相互独立。

记相依成分φ1(xt-1-u )+φ2(xt-2-u )+…+φp(xt-p-u )为ηt，随机成分u+εt为ut，可将xt表示为相依成分与随机成分之和：

其中，ηt与ut相互独立，E( xt)=u，E( ut)=u，E(ηt)=0。

水文序列xt与其所包含的相依成分ηt的相关程度可由相关系数r来描述：

根据文献［21］所建立的相关系数与自回归模型参数之间的关系，有：

式中，ρi(i=1，2，…，p )为序列的自相关系数，由于自回归系数φi(i=1，2，…，p )可采用Yule-Walker方程估计，故式（7）可写为：

鉴于自相关系数ρi(i=1，2，…，p )是描述水文时间序列自身内部线性相依程度的指标，可判断序列是否独立。而式（8）说明水文序列与其相依成分之间的相关系数可以综合考虑1阶到p阶自相关系数的影响，因此相关系数也可用于水文序列独立性检验以及表征其相依变异程度。

进一步分析AIC和BIC准则的表达形式，式（2）和式（3）均由两个部分组成。前一项为拟合残差方差量，反映了模型的拟合误差，后一项为包含序列长度与模型阶数的惩罚项，反映了模型不确定性的大小。显然，实际运用中需要模型拟合的精度越高越好，但是过高的精度意味着参数的增加，使得模型复杂化、不确定性增加，反而又影响模型的精度［34］。因此，AIC、BIC准则是通过拟合误差项与不确定性惩罚项两项相互平衡，在准则最小值点处取得模型的理想阶数和对应参数。

根据有限的实测资料（样本）计算出来的相关系数必定存在抽样误差，为了判断样本相关系数的可靠性，通常按照统计学原理计算相关系数的均方误差［35］。由于相关系数r可以表示序列的相依变异程度，其均方误差σr则可视为表征水文相依变异序列的拟合误差的统计量，计算公式为：

式中n为样本序列长度。

当模型阶数增大时，均方误差随着相关系数的增大而减少，这意味着原始序列与相依变异成分的拟合程度增加，不确定性减少。信息熵指标主要用于描述和度量数据的无序性和信息量，其与变量的不确定性成正相关关系［36］。研究水文过程的不确定性时，时间序列的信息熵越大，表明其不确定性也越大。信息熵定义为：

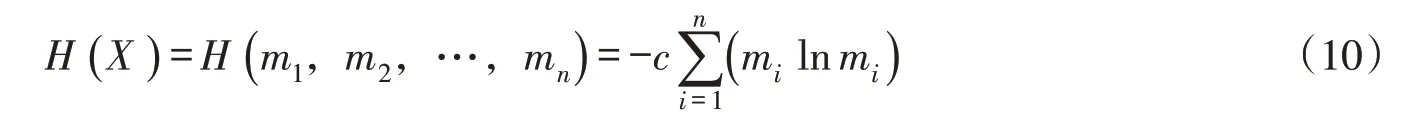
式中：X为任意一个随机变量；mi为第i个信息状态出现的概率；H(m1，m2，…，mn)为熵函数；c为常数（一般取为1），对于等概率信息系统有为自然对数。

针对AR（1）和AR（2）模型，借用信息熵的形式，构造与模型阶数相关可反映模型不确定性的函数式如下：

H（2）中包含H（1）中的信息量，当序列长度n ≫p时，表示AR（p）模型不确定性的函数式可写为：

对于式（12）而言，其函数值随着阶数增大而增加，意味着模型参数增加将导致模型不确定性增加。

结合式（9）与式（12），这两个成分正好与AIC 准则和BIC 准则中的前后两项所表示的意义相同。因此，可得到用相关系数的均方误差表示模型拟合误差、借用信息熵形式的函数式作为惩罚项的定阶准则，简称RIC准则，其表达式为：

式中：p为模型阶数；n为序列长度；σr为相关系数的均方误差。

为与AIC、BIC准则具有统一格式，将上式进一步写为：

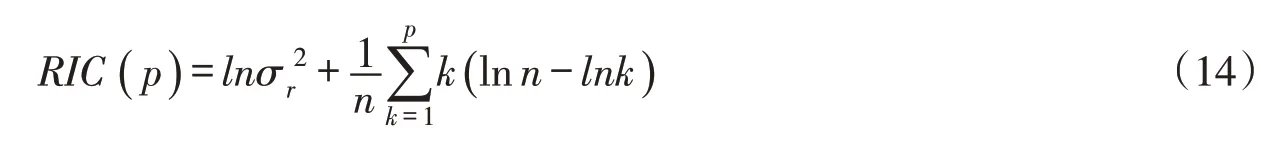
与AIC、BIC准则类似，当RIC准则函数值最小时所对应的阶数即为模型的理想阶数。

由于RIC 准则是基于水文序列与其相依成分之间的相关系数所构建，而相关系数的大小可以表征序列的相依变异程度。根据统计学原理和相关系数检验取值范围，当序列长度、模型阶数已知时，可计算在显著性水平α 、 β(α ＞β )下的相依变异程度对应的分级阈值rα、rβ，并进一步将相依变异程度划分为5个等级［37］，见表1。同时，可利用相依变异程度分级结果进行水文序列的独立性检验，即当序列无变异时则说明序列是独立的，有其他不同程度的相依变异时则还含有相依成分。

表1 相依变异程度分级与水文序列独立性检验

综上，以自回归模型为例利用RIC准则确定序列相依变异成分阶数的具体步骤为：（1）去除原始序列包括跳跃、趋势和周期在内的确定性成分，得到剩余序列成分；（2）绘制剩余序列的自相关系数图、偏相关系数图。若自相关系数图拖尾，偏相关系数图截尾，则认为剩余序列存在AR（p）相依成分；（3）设定模型阶数上限值，从1阶递增阶数，利用最小二乘法（或递推算法）估计模型参数，计算估计的相依成分与剩余序列的相关系数；（4）选择RIC准则函数取得最小值时的阶数为模拟模型暂定的阶数p，并判断剩余序列的相依变异程度；（5）序列独立性检验与最终阶数确定，若相依变异程度分级结果为无变异则序列独立，确定模型阶数为零阶，否则模型的理想阶数为p 阶；（6）模型检验，利用RIC 准则对残差序列再次定阶后，依据相依性分级结果进行独立性检验，若残差序列独立则模型符合“相依有变异而残差无变异的最小阶数”的检验标准，否则模型阶数p=p+1，重复本步骤直至残差序列独立为止（由于统计方法有抽样误差，因此任何一种定阶准则均有失误的可能）。

4 RIC准则验证

4.1 统计试验验证依据式（14），水文序列相依成分定阶的RIC准则中的前一项均方误差体现了1～p阶自相关系数对水文序列相依性的影响，后一项体现了模型阶数对序列随机性的影响，因此RIC 准则可以确定序列的阶数。现分别以1阶、2阶、3阶和4阶自回归模型为例，模拟生成含有相依变异成分的序列，并利用统计试验将RIC准则定阶的准确率与AIC准则、BIC准则进行比较，以说明RIC准则定阶的有效性。

4.1.1 AR（1）模型 1 阶自回归模型AR（1）模型的表达式为xt=φ1()xt-1-u +ut。根据Yule-Walker 方程可得ρ1=φ1，带入式（8）得：

根据基于相关系数的水文相依性变异分级方法，上式可以作为检验序列是否存在相依变异的依据，令α=0.05，β=0.01，试验中要求序列为中及以上程度的变异；同时，AR（1）模型平稳的条件为|φ1|＜1。现设计统计试验模拟生成相依序列，其中假设纯随机序列ut的均值u=100、变差系数Cv=0.2，偏态系数CS=0.4，并假设其服从P-Ⅲ型分布。具体步骤如下：

（1）在基于相关系数的水文相依性变异分级方法检验序列存在变异，且满足平稳性的条件下，随机生成自回归系数φ1，设序列长度分别为n=50，75，100，150和200；（2）当n=50时，先生成符合假设条件的随机序列ut，并设初始值x1=100，再生成1 阶自回归序列xt；（3）假定模型阶数可取之间的所有整数［38］，在阶数选定条件下计算模拟序列与原始序列的残差方差σε2，由AIC、BIC 准则确定模型阶数，并计算原序列与模拟相依部分的相关系数，再由RIC 准则确定模型阶数；（4）在条件范围内随机生成1000组φ1值，按步骤（2）与（3）统计由准则确定模型阶数为1阶的组数，除以1000 即可分别求得3 个准则在序列长度为50 时的定阶准确率；（5）重复上述步骤，改变序列长度n，计算不同序列长度下的准则定阶准确率，取其平均值作为1阶自回归模型在不同准则下的平均定阶准确率。

表2为AR（1）模型在序列长度不同时的定阶准确率。结果显示，对于AR（1）模型而言，RIC准则的平均定阶准确率高于BIC准则，且远高于AIC准则。不论序列长度如何，RIC准则的定阶准确率均在90%以上，说明该准则对于AR（1）模型的阶数确定具有很高的准确性。

4.1.2 AR（2）模型 2 阶自回归模型AR（2）的表达为根据Yule-Walker方程可得将其带入式（8）得：

上式可以作为检验序列是否存在相依变异的依据。同时，为满足平稳性条件，φ1、φ2需满足如下关系式：

按照上述AR（1）模型试验思路，纯随机序列ut的统计参数不变，试验步骤一致，得到AR（2）模型的定阶准确率。表3 结果显示， RIC 准则的准确率在所有准则中最高，平均定阶准确率为80.06%，并且随着序列长度增加而提高，说明了RIC 定阶准则对于AR（2）模型的阶数确定具有较高的准确性。

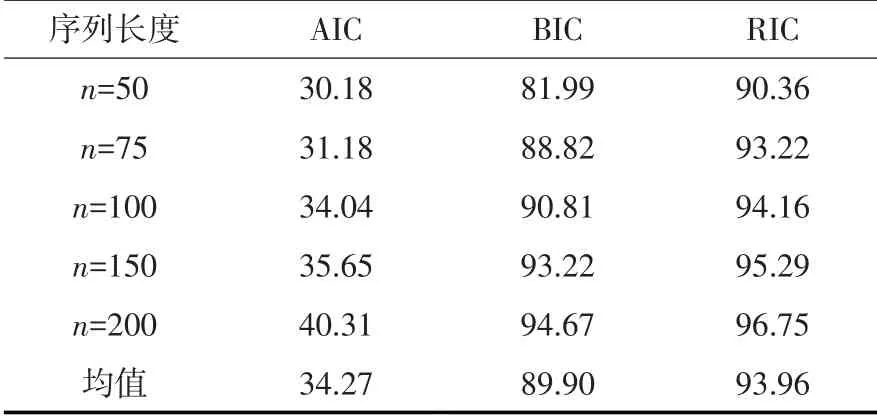
表2 AR（1）不同序列长度和准则下的定阶准确率（单位：%）

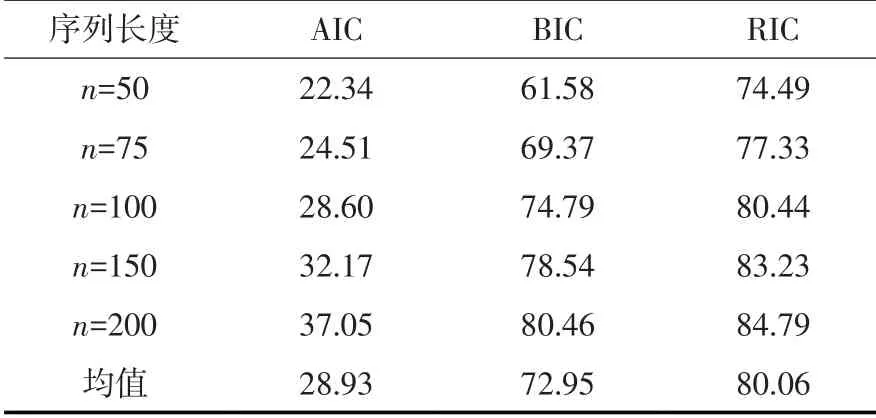
表3 AR（2）不同序列长度和准则下的定阶准确率（单位：%）

4.1.3 AR（3）模型 3阶自回归模型AR（3）的表达式为由于此时通过相关系数检验模拟序列相依变异与否对后续试验结果影响很小，所以只考虑在平稳条件下生成相应的φ1、φ2和φ3。而超过3阶的AR模型的自回归系数的判别条件越来越复杂，这里采用特征根法进行判断［39］。

按照相同的试验思路可以得到AR（3）模型的定阶准确率，如表4所示。当RIC准则运用于AR（3）模型时，其定阶准确率在不同序列长度时均高于其他准则，且随着序列长度增加而提高；其中在序列长度为200时，RIC准则的准确率为71.67%，平均定阶准确率为63.56%，说明RIC准则对于AR（3）模型的阶数确定具有一定的准确性。

4.1.4 AR（4）模型 4 阶自回归模型AR（4）的表达φ4(xt-4-u )+ut，在平稳约束条件下生成φ1、φ2、φ3和φ4，与AR（3）模型同理可以得到AR（4）模型的定阶准确率。根据表5结果显示，对于AR（4）模型，3个准则的定阶准确率均不算高，其中RIC准则的定阶准确率有时会略低于BIC 准则，但明显高于AIC 准则，其平均定阶准确率为53.52%，说明RIC准则对于AR（4）模型也具有一定的适应性，但因为阶数增大致使计算中不确定性增多，其准确率比1至3阶时有所降低。

表4 AR（3）不同序列长度和准则下的定阶准确率（单位：%）

表5 AR（4）不同序列长度和准则下的定阶准确率（单位：%）

4.2 实例分析验证为进一步说明RIC 定阶准则的有效性和实用性，选取实测水文序列进行验证，包括澜沧江允景洪站的年径流序列（1957—2014年）、长江螺山站的月径流序列（1953—2016年）、长江宜昌站的月径流序列（1946—2016年）以及西江梧州站的年径流序列（1900—2000年）。按照RIC准则定阶的步骤，首先去除序列的确定性成分。应用Pettitt 法、Brown-Forsythe 法和滑动T检验法等识别序列的跳跃成分［40］；应用Spearman秩次相关检验法、Kendall秩次相关检验法和线性趋势相关系数检验法等检测其趋势成分［41-42］；应用功率谱分析法、谐波分析法和最大熵谱分析法等识别其周期成分［43］。然后绘制剩余序列的自相关系数图和偏相关系数图，结果见图1，其中虚线为显著性水平等于0.05时的容许上、下限。若自相关系数处于上、下容许限之间，认为序列独立随机；反之则序列存在相依变异。模型阶数可由偏相关系数图的截尾性初步判断。

图1 实测水文序列自相关及偏相关系数

图1结果显示，除允景洪站外其余序列均存在相依变异，螺山站、宜昌站和梧州站序列分别为1、2、3阶偏相关系数截尾、自相关系数拖尾，因此以上序列均可采用AR（p）模型建模。在利用RIC准则定阶过程中，设定模型阶数上限为计算模型为不同阶数时的模型参数估计值、序列与其相依成分的相关系数以及RIC准则的函数值。取RIC函数最小值对应的阶数为模型阶数，判断序列相依变异程度并用分级方法进行残差独立性检验。表6显示了不同准则下序列阶数的确定情况以及RIC定阶准则下的序列相依变异程度的判定与残差独立性检验结果。

表6 实测水文序列阶数确定及相依变异程度分级结果

由RIC准则判定的允景洪站年径流序列为1阶，但其相依变异程度为无变异，因此最终确定为0阶，这与其自相关系数图情况吻合。说明RIC 准则在定阶过程中可进行序列独立性检验且具有较好的效果，而其他准则无法满足此需求。依据不同准则的判定结果，总体上RIC准则与BIC准则确定的阶数在多数情况下是一致的。由RIC 准则与BIC 准则确定的螺山站、宜昌站和梧州站序列分别为1、2、3阶，这与三站偏相关系数图显示的截尾阶数一致，说明RIC准则对于AR（1）、AR（2）、AR（3）模型都具有一定的适应性。但AIC准则显示阶数存在偏高的情况，例如螺山站为3阶，梧州站为17阶。

为确定序列最合理的阶数，提出“相依有变异而残差无变异的最小阶数”的检验标准，即选取使得序列存在相依变异且残差不存在变异的最小阶数为最终阶数。绘制各站径流序列与其相依部分的相关系数r随阶数的变化图，如图2所示，上下两条虚线分别表示显著性水平为0.01和0.05时的相关系数临界值。若相关系数位于虚线以上，则表示此阶数的模拟序列存在相依变异，反之无变异。

图2 相关系数随阶数变化

图2（a）中允景洪站年径流序列各阶数的模拟序列均不存在相依变异；图2（b）中螺山站月径流模拟序列为1阶时，模拟序列存在相依变异，而由表6可知，此阶数时残差序列独立，故满足“相依有变异而残差无变异的最小阶数”的检验标准；同理，在图2（c）（d）中，宜昌站月径流模拟序列与梧州站年径流模拟序列分别为2阶和3阶时，取得满足检验标准的最小阶数。由此说明RIC准则与BIC准则定阶结果合理，而AIC 准则定阶结果偏高。为直观显示这4个序列分别为0、1、2、3阶时的相依变异情况，将其绘制成图（见图3），其中实线为其拟合的相依成分。根据图示，由相依部分代表的模拟序列与原序列的变化情况较为一致，进一步说明RIC准则定阶的合理性。

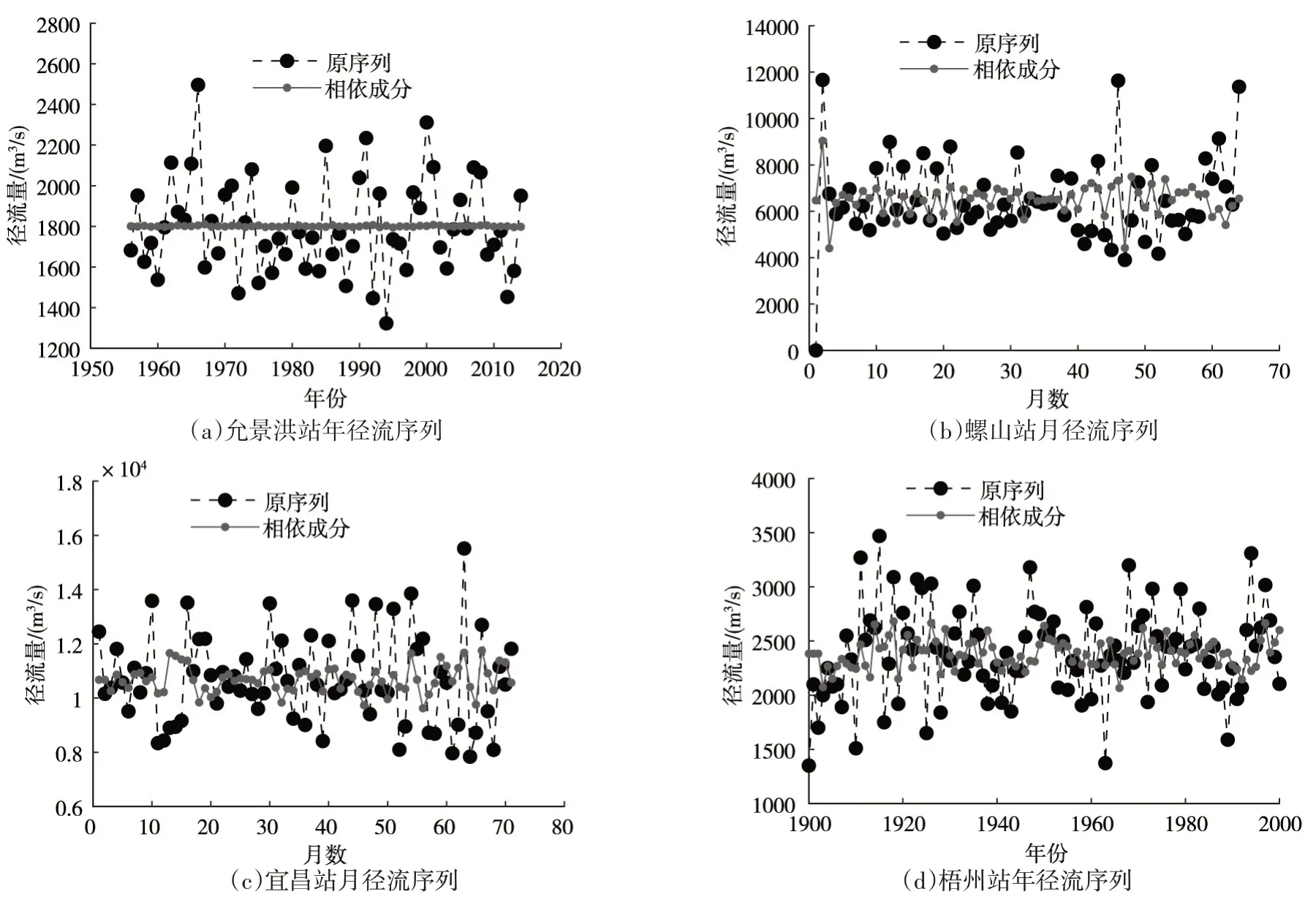
图3 实测径流序列相依成分示意

进一步分析表6中实测序列的残差独立性检验结果，在由RIC准则确定阶数的条件下，模型的残差项均为独立序列，表明由RIC 准则所确定的模型满足使用条件且具备一定的准确性。综上，在统计试验和实测验证中，RIC准则定阶结果的准确性均优于AIC准则，接近或优于BIC准则，且满足检验要求，并且RIC准则在定阶过程中可进行序列的独立性检验。

5 结语

水文过程常常存在一定的相依性，这使得含有相依成分的时间序列无法满足水文计算中一致性的假设，因而造成了研究中的诸多困难。针对非一致性水文序列所表现的相依性特点，本文以自回归模型为例，提出了一种基于相关系数的RIC 定阶准则以建立适当的模型描述相依变异成分。主要结论如下：（1）RIC准则由表示相依拟合程度的相关系数的均方误，以及表示序列不确定性的惩罚项构成。对于AR（1）、AR（2）、AR（3）和AR（4）模型，统计试验表明序列长度越大，RIC准则定阶的准确率越高，且其准确率接近或高于BIC准则，远高于AIC准则，说明了RIC准则在水文相依变异序列阶数识别中的有效性；（2）将RIC准则用于允景洪站、螺山站、宜昌站和梧州站的实测水文序列进行验证，实例分析表明，定阶结果与自相关系数图、偏相关系数图表现的情况一致，且满足“相依有变异而残差无变异的最小阶数”的检验标准，说明了此方法的合理性；（3）RIC准则定阶过程中可以基于相关系数进行序列独立性检验，以及定阶完成后可进行模型检验，克服了其他准则定阶过程中的局限性；（4）RIC准则可以作为其他定阶准则评价的标准，RIC准则与BIC准则在统计试验的准确率以及实测序列的定阶结果上较为一致，均优于AIC准则，因此RIC准则较AIC准则对于相依变异成分的阶数识别更具有适应性，建议实际定阶中主要参考RIC准则与BIC准则定阶结果。

此外，由于实际中基于AR模型的水文序列预测与延展工作通常以低阶为主，对于高阶模型的阶数确定的方法与准确性仍然是难点问题，本文只完成了4阶以内的自回归模型的统计试验与部分含有低阶数相依变异成分的实例分析，所以至于RIC 准则对于更高阶数的自回归模型以及其它相依模型的适应性尚需进一步研究。