基于数值模拟方法再生混凝土梁弯曲延性分析*

姚大立， 杨卫闯， 魏 华， 余 芳

(沈阳工业大学 建筑与土木工程学院， 沈阳 110870)

随着建筑领域的飞速发展，建筑垃圾逐年增加，再生混凝土的研究逐渐进入学者们的视野.所谓再生混凝土是指废弃混凝土经过人工破碎、清洗和分级按照一定比例部分或全部代替天然粗骨料的新型混凝土[1]，其不仅具有节能、环保的优点，而且符合我国可持续发展的方针.

钢筋混凝土梁作为受弯构件是土木工程中数量最多、使用最广的一类构件，是建筑结构中的重要组成部分[2].随着计算机技术和有限元理论分析的不断发展，有限元分析软件对建筑结构和实际工程的应用越来越普遍[3]，本文在已有研究成果[4]的前提下，利用ABAQUS有限元分析软件对完全再生混凝土梁进行数值模拟，验证模型的正确性，分析再生混凝土少筋梁、适筋梁和超筋梁的界限配筋率以及再生混凝土梁的弯曲延性.

1 试验设计

为验证再生混凝土本构关系和模型建立的正确性，采用文献[4]中部分试验数据进行对照，再生混凝土梁的截面尺寸为120 mm×120 mm，长度为1.5 m，跨度为1.2 m，试件采用3等分点加载，试验参数采用文献[4]中实测值，配筋形式与文献[4]保持一致，试验参数如表1所示.

2 有限元模拟分析

2.1 材料本构关系

再生混凝土受压本构模型采用文献[5]研究成果，具体计算公式为

表1 梁试验参数Tab.1 Experimental parameters for beams

(1)

式中：x=ε/εc；y=σ/σc；σ为混凝土压应变为ε时的混凝土压应力；εc为混凝土峰值压应变，εc=σc/Ec；Ec为混凝土弹性模量；σc为混凝土峰值压应力，即轴心抗压强度实测值fc.

再生混凝土受拉本构模型采用文献[6]研究成果，具体计算公式为

(2)

钢筋的本构模型采用双直线模型[7]，具体计算公式为

(3)

式中：σs、ε分别为钢筋的应力和应变；fyt为钢筋的屈服应力；Es为钢筋的弹性模量.

2.2 单元选取及模型建立

模型的建立共分为5个部件，即混凝土、垫块、箍筋、受压钢筋以及受拉钢筋.混凝土和垫块单元采用C3D8R，箍筋、受拉钢筋以及受压钢筋采用T3D2.考虑到模型的收敛性，并未设置钢筋与混凝土之间的粘结滑移，采用混凝土损伤塑性模型来定义混凝土的塑性特性[8].混凝土与垫块的网格划分尺寸为40 mm，钢筋的网格划分尺寸为25 mm，收敛结果良好.有限元分析模型如图1所示.

图1 有限元分析模型Fig.1 Finite element analysis model

2.3 边界条件及加载方式

边界的设置与实际试验的约束完全一致，在垫块底部中线位置设置约束，左侧支座对三个自由度进行约束，右侧支座对两个自由度进行约束.加载制度与试验保持一致，采用单调位移加载的加载方式.

3 模拟结果分析

图2 荷载挠度曲线Fig.2 Loading-deflection curves

表2 极限弯矩试验值和模拟值Tab.2 Experimental and simulated values of ultimate bending moment

4 弯曲延性分析

延性是指构件在达到极限承载力后，抵抗其变形的能力.为降低构件在外力作用下的脆性破坏，应考虑混凝土的延性设计，这对结构安全有重要意义，在抗震设防地区更加重要.

本文为精确分析再生混凝土少筋梁、适筋梁和超筋梁的界限配筋率以及不同配筋率、混凝土强度和混凝土种类的延性发展规律，对10根不同配筋率和3种混凝土强度及混凝土种类共13根梁进行数值模拟(钢筋采用HRB335)，具体参数设计和模拟结果如表3所示.

4.1 荷载挠度曲线

表3 模型梁参数及模拟结果Tab.3 Parameters and simulated results of model beams

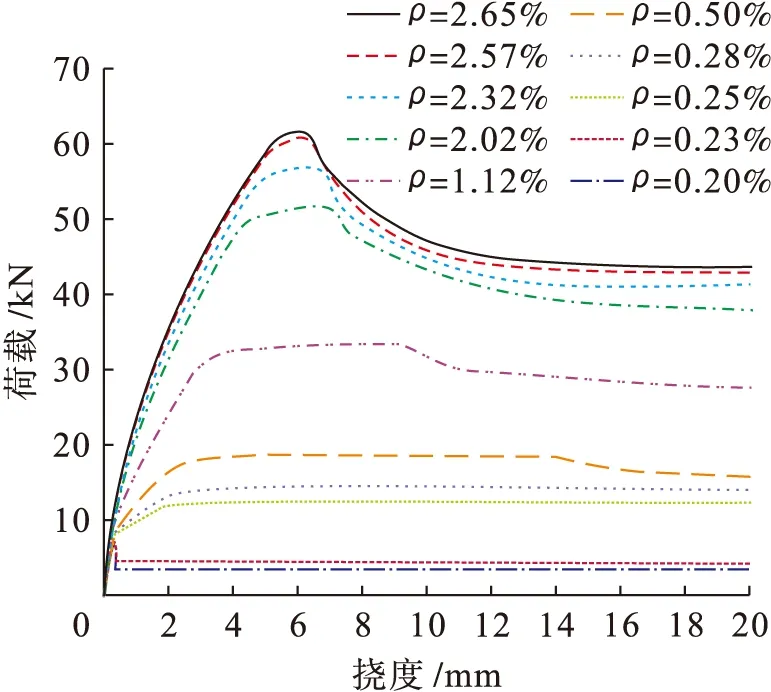
图3 不同配筋率下荷载挠度曲线Fig.3 Loading-deflection curves under different reinforcement ratios

图4 混凝土强度对荷载挠度曲线的影响Fig.4 Effect of concrete strength on loading-deflection curves

图5 混凝土种类对荷载挠度曲线的影响Fig.5 Effect of concrete type on loading-deflection curves

4.2 延性系数评定指标

为了便于评定再生混凝土梁的弯曲延性指标，本文引入延性系数，即

μ=Δu/Δy

(4)

4.3 配筋率对弯曲延性的影响

根据表3中的数据绘制出延性系数随配筋率的变化曲线，如图6所示.再生混凝土的少筋梁和超筋梁对应的延性系数均较小，其值均在1～2之间，延性明显不足，表现出明显的脆性破坏特征.在适筋梁范围内，梁的弯曲延性系数随着配筋率的减小而增大，这说明在适筋梁范围内，最小配筋率具有最好的变形能力，这一特征与普通混凝土梁相似.

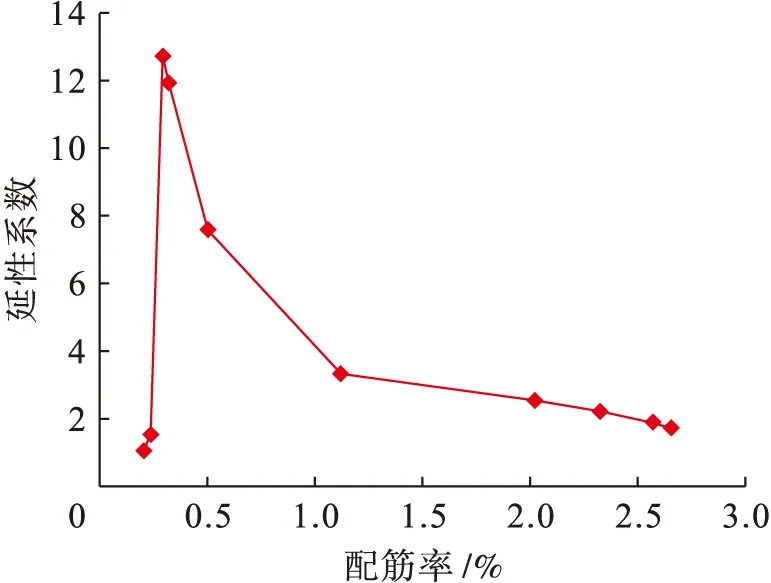
图6 配筋率延性系数曲线Fig.6 Reinforcement ratio-ductility coefficient curve

4.4 混凝土强度对弯曲延性的影响

根据表3的数据绘制出混凝土强度对延性系数的变化曲线，如图7所示.当混凝土强度从C30分别增大到C40和C50时，延性系数分别增加25.2%和14.98%，由此可见，随着再生混凝土强度的提高，延性也随之增大.

图7 混凝土强度对延性系数的影响Fig.7 Effect of concrete strength on ductility coefficient

4.5 混凝土种类对弯曲延性的影响

由表3可知，普通混凝土梁的延性系数为2.846，再生混凝土梁的延性系数为3.35，再生混凝土梁比普通混凝土梁的延性系数提高了17.7%，再生混凝土梁的延性与普通混凝土梁相比较好.这主要是因为再生混凝土梁在峰值荷载过后，其刚度退化速率较慢导致的.

5 结 论

本文通过分析得出以下结论：

1) 基于试验数据，利用ABAQUS有限元分析软件验证了再生混凝土梁模型的正确性.

2) 再生混凝土梁的弯曲延性较普通混凝土梁好，在适筋梁范围内，最小配筋率对应梁的弯曲延性最大，变形性能最好.

3) 再生混凝土梁的最小配筋率与普通混凝土梁基本相同，最大配筋率较普通混凝土梁降低约17.2%.本文建议再生混凝土梁的最小配筋率为0.25%，最大配筋率为2.32%.