基于一致性算法的智能电网储能单元分布式调度策略*

胡诗尧， 安佳坤， 韩璟琳， 孙鹏飞， 刘雪飞

(国网河北省电力有限公司 经济技术研究院， 石家庄 050000)

随着全球能源危机日益严重及社会对环境保护需求的增长，人们迫切需要更高效、更环保、更经济的电力供应[1]，因此，提出了智能电网的概念，通过智能化管理电力的生产、运输和零售过程来保证电力系统安全、可靠、经济的运行[2].

目前，智能电网通过大力发展可再生资源发电来减少对火力发电的依赖[3]，但可再生资源发电具有随机、波动和间歇性强的缺点，将其并入电网将会对电网产生冲击并影响电力系统的调峰能力[4].随着电池储能和超级电容储能等新型储能技术的快速发展和产业化[5-6]，结合可再生资源发电功率的预测技术与海量储能单元功率双向流动的特性来平抑大规模可再生资源发电并网所产生的功率波动，已逐渐成为研究及应用的热点[7-8].

由于太阳能和风能等可再生能源具有不确定性，故需要实时调整智能电网储能系统的输出功率来补偿实际功率与计划功率间的偏差[9].然而，海量储能单元存在地理位置分散难以获取同步和全局信息的问题，传统的集中式调度方法灵活性低，无法满足智能电网对储能单元“即插即用”的需求[9].而分布式调度方法仅需局部信息的交互即可实现储能单元的实时功率分配，具有更好的灵活性和鲁棒性[10].分布式调度策略通过应用一致性算法来实现储能单元的实时功率分配，如文献[11]通过仿真分析揭示了不平衡量的反馈系数、通信拓扑结构和网络规模对分布式调度算法收敛速度的影响；文献[12]利用矩阵论和图论分析了通信时延与一致性算法收敛速度间的关系.

本文基于一致性算法[13]实现储能单元的调度，从而抑制可再生能源发电所引起的功率波动，该调度考虑储能单元的内阻对充放电效率的影响，通过引入一致性算法实现充放电效率的最大化.

1 储能单元分布式调度模型

假设有n个储能单元分散配置在配电网中，构成一个分布式储能网络，每个储能单元均有一个计划输出功率，该功率由调度策略决定.当可再生能源的输出功率发生波动时，需要根据一定的原则调整储能单元的实时功率.为了实现抑制可再生资源发电功率波动的效果，本文使用一致性算法实现功率在储能单元中的公平分配，即在保证储能单元充放电状态不变的同时，确保每个储能单元的输出值与计划输出功率成比例.

智能电网的有功平衡式可表示为

(1)

式中：PB，i为储能单元的充放电功率；PG，k、PD，j分别为发电机与负荷的需求功率；SG、SD、SB分别为智能电网中的发电机、负荷和储能单元.电网中储能单元需要提供的总有功功率为

(2)

当PL>0时，表示储能单元充电；当PL<0时，表示储能单元放电.为了保证智能电网功率的平衡，本文使用调度策略来控制储能单元的充放电功率PB，i(i∈SB)来调整PL，即

(3)

由于储能单元也存在一定的内阻，故在充放电时会存在功率损耗，即

(4)

(5)

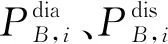
由于放电状态可以由充电状态表示出来，本文为了简化分析，仅考虑储能单元运行在充电状态时的情况.储能单元的实际充电功率为

(6)

为了使智能电网更经济运行，需要最小化网络损失，即通过调整储能单元的充电参数最大化式(6).本文通过协调控制目标函数来保证智能电网在快速变化时仍可进行快速、稳定地调控，即

(7)

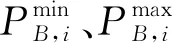
由文献[13]可知，储能单元的充电速率αi与充电功率PB，i线性表达式为

αi=ai-biPB，i

(8)

式中，ai、bi为常系数.

将式(8)代入式(7)可得目标函数为

(9)

文中定义储能单元的边际成本(λi)为式(9)相对于充电功率PB，i的偏导，即

λi=ai-2biPB，i

(10)

2 分布式调度策略

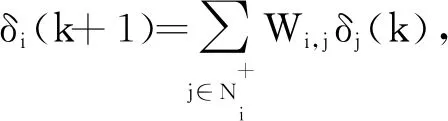
(11)

式中：Pi(0)为储能单元i的初始功率，本文实验设置为40 kW；ΔPi(0)为需要调整的功率偏差值.

实时功率分配策略为

(12)

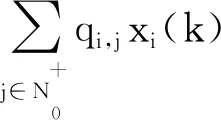
将式(12)转化为矩阵的形式来分析分布式调度策略的性质和收敛性，即

(13)

式中：λ、ΔP、x、C、Q分别为λi、ΔPi、xi、Ci、q的向量形式；ΔP(k+1)-ΔP(k)为控制所有储能单元达到最优值的反馈机制.由式(13)则有

x(k+1)=Qx(k)-(ΔP(k+1)-ΔP(k))

=x(k)-(ΔP(k+1)-ΔP(k))

⟹x(k+1)+ΔP(k+1)

=x(k)+ΔP(k)

(14)

式中，x(k)+ΔP(k)取任意的k均为一常数.由初始值xi(0)和ΔPi(0)可得到∑xi(0)+ΔPi(0)=ΔPΣ，因此，x(k)=ΔPΣ-ΔP(k)为需要调节的功率偏差量，其值可由储能单元系统的分布式调度获得.

将式(13)代入式(14)则有

x(k+1)=(Q-εC)x(k)+C(I-P)λ(k)

(15)

将式(14)和式(15)矩阵化则有

(16)

定义

(17)

则式(17)所示的系统矩阵可以看做被εΔ扰动的下三角M矩阵，构造向量为

(18)

(19)

式中，VT、φ满足VTφ=I.

当扰动ε>0时，随着ε的增大，矩阵M的特征值k2逐渐减小.假设ε≤ξ1，则|k2|<1.因为M的特征值与ε有关，故存在上界ξ2，使得当ε≤ξ2时，|kj|<1，j=3，4，…，N.综上所述，当ε≤min(ξ1，ξ2)时，M具有特征值k1=1，且其他特征值位于单位圆上.此时，特征向量为[1，0]T，当k→∞时，[λ(k)，x(k)]T收敛到[1，0]T，所以当ε足够小时，系统能稳定运行且所有储能单元能收敛到最优特征值λ*.

3 仿真与案例分析

图1 IEEE27节点系统拓扑图Fig.1 Topological diagram of IEEE27 node system

27节点仿真结果如图2所示，图2a、b、c展示了储能单元1、13和27的λ、PB和ΔPB的变化情况，图2d为27条母线总PL变化情况.根据图2可知，27个储能单元能收敛到相同值且总储能功率为2 000 kW.

表1 储能单元常系数Tab.1 Constant coefficients of energy storage units

图2 分配策略有效性仿真结果Fig.2 Simulation results for effectiveness of distributed strategy

本文在图1系统保证总储能值不变的情况下接入第28个储能单元，接入后的系统拓扑图如图3所示，第28个储能单元的ai为0.874，bi为0.008 5.仿真实验结果如图4所示，图4a、b、c展示了储能单元1、13、27和28的λ、PB和ΔPB的变化情况，由图4a、b、c可以看出，在接入节点28后，三项指标值虽然有一定的变化，但最终均收敛于一致；图4d为28条母线总PL变化情况，从图4d中可以看出，在接入新的储能单元后，系统边界成本先出现短暂波动，然后收敛并趋于一致，且未引起PL较大变化，表明系统能满足对储能单元即插即用特性的需求，可以针对太阳能和风能的不确定接入作出良好的反应，更适合用于实际工况.

图3 IEEE28节点系统拓扑图Fig.3 Topological diagram of IEEE28 node system

4 结 论

为了实时调整智能电网储能系统的输出功率，以补偿实际功率与计划功率间的偏差，本文建立了储能单元分布式调度模型，并提出了一种基于一致性算法的智能电网储能单元分布式调度策略.该调度考虑了储能单元内阻对充放电效率的影响，通过引入一致性算法实现充放电效率的最大化.IEEE27节点系统和即插即用特性仿真结果表明，所提出的分布式调度策略能保证所有储能单元可以收敛到同一个最优值，克服了可再生资源发电具有随机、波动和间歇性强的缺点，满足太阳能及风能等不确定工况需要.

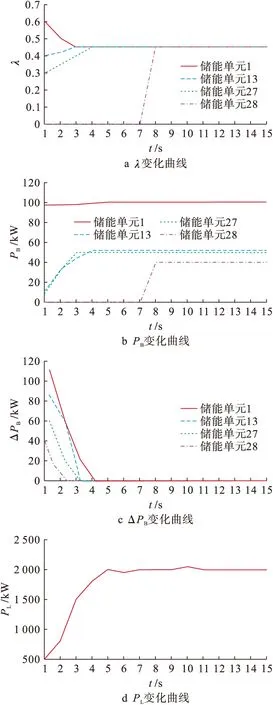
图4 即插即用特性仿真结果Fig.4 Simulation results of plug and play characteristics