基于MATLAB的四杆并联机械臂工作空间仿真与分析

黄俊华 田壮

摘 要：目前在许多食品、机械加工等行业的自动化生产线上普遍存在抓取和分拣等大量的重复性工作，为了降低劳动成本，提高生产效率，实现高效益，提高生产的安全可靠性，推动并联机械手的发展非常有必要。本文介绍了一种与Delta机器人结构相似的四杆并联机器人，利用了蒙特卡洛法，通过MATLAB编程求解得到了一种四杆并联机械臂工作空间的仿真结果，对仿真结果的分析为以后四杆并联机械臂的结构优化和设计奠定了基础。

关键词：并联机械臂;工作空间;MATLAB

DOI：10.16640/j.cnki.37-1222/t.2019.20.108

0 引言

Delta型机器人有着闭环并联的拓扑结构，承载能力强、结构强度大、运动精度高，近年来国内外许多学者对Delta型的机械结构进行了研究，在其运动学正解、运动学反解、工作空间和运动轨迹规划等方面取得了许多成果。本文研究了一种四杆并联机械臂，其结构特点与Delta并联机器人相似，四杆并联机械臂为冗余机构，稳定性得到了提高，适用于大负载、较复杂的工作环境，并联机械臂的诸多优点为其在工业自动化上的应用提供了广阔的发展前景，对四杆并联机械臂的工作空间仿真及分析对其未来的实际应用具有重要意义。

1 四杆并联机械臂的结构模型

Delta并联机器人具有三个自由度，其基座平台和运动平台都呈等边三角形，有三个平行四边形机构。本文研究的四杆并联机械臂与Delta并联机器人有相似之处，即都具有平行四边形机构，且执行机构都具有三个自由度，但四杆并联机械臂的基座平台（即静平台）和运动平台都呈正方形，有四个平行四边形机构，这是它们之间的不同点。本文设计的四杆并联机械臂等效简化结构模型如图1所示。

2 四杆并联机械臂运动学分析

对四杆并联机械臂的运动学分析是求解其工作空间的基础，包括运动学反解分析和运动学正解分析。简单来说，运动学反解分析就是已知末端执行器的空间位置，求解并联机械臂各驱动电机所需的运动转角;运动学正解分析就是已知并联机械臂各驱动电机的转角，求解末端执行器所在的空间位置。

3 四杆并联机械臂工作空间仿真

（1）工作空间求解方法。目前常用的求解机械臂工作空间的方法主要分为三类：几何法、解析法和数值法。其中，几何法多用于平面机器人的工作空间求解，直观性较强，但求解多自由度机械臂的工作空间时精度较差。解析法则是基于雅克比矩阵来求解串联或并联机械臂工作空间的方法，求解过程较复杂，所以一般只用在关节数少于3个的机械臂，应用范围较窄。数值法是基于正向运动学求解工作空间的方法，根据杆件空间关系列向量方程组，适用于多种形式的机械臂结构，目前在这三种方法中应用最多。（2）蒙特卡洛法。本文研究通过数值法求解四杆并联机械臂的工作空间。蒙特卡洛法是一种常用的求解机械臂工作空间的数值方法，是基于随机抽样来解决数学问题的一种方法。在求解机械臂工作空间时，首先通过蒙特卡洛法随机抽取大量不同的机械臂驱动电机转角变量组合，再将这些变量组合代入机械臂的正向运动学方程中，计算出机械臂末端执行器在空间坐标系的坐标值，将坐标值在空间坐标系中画出来，它们围成的空间就可以近似代表机械臂末端执行器在空间中可运动的范围。随机抽取的电机转角变量组合越多，仿真模拟所得的机械臂工作空间越接近其实际的工作空间。

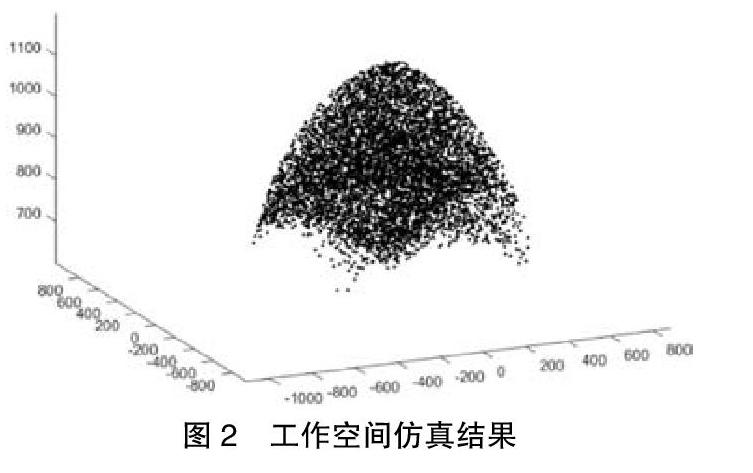
利用蒙特卡洛法求解四杆并联机械臂的工作空间可以分成三步：首先，利用MATLAB中的随机函数rand（）产生四杆并联机械臂各驱动电机转角变量的随机值;其次，将电机转角变量随机值带入四杆并联机械臂的正向运动学方程中，得到四杆并联机械臂末端执行器参考点在静坐标系中的空间位置坐标;最后，利用MATLAB将每个计算得到的末端执行器参考点的位置坐标描绘标注在静坐标系中，得到四杆并联机械臂的仿真工作空间。通过MATLAB仿真求解得到的四杆并联机械臂的工作空间如图2所示。

4 仿真结果分析

由2所示的四杆并联机械臂工作空间仿真结果可以发现：四杆并联机械臂的工作空间的顶部是一个纺锥形，其最顶点代表了该机械臂在竖直方向上运动的“上极限”位置，底部中间是一个“峰”形的突起，“峰”顶代表了该机械臂在竖直方向上运动的“下极限”位置，而且底部四周也有四个小的“峰”形突起，这四个小“峰”对应着四杆并联机械臂在水平方向的极限位置。

5 结论

对一种四杆并联机械臂基于MATLAB的工作空間仿真与分析为其工作空间的优化和结构设计提供了基础与依据。通过对其仿真工作空间的分析，可以得到四杆并联机械臂的工作范围，即机械臂末端执行机构在竖直方向、水平方向的最大距离，在设计以后设计四杆并联机械臂的结构时，可根据工作空间需求来设计，这对提高设计效率、节约成本等都有重要意义。

参考文献：

[1]王娜，王冬青，赵智勇.三自由度Delta并联机械手运动学分析及轨迹规划[J].青岛大学学报（工程技术版），2017，32（01）：63-68.

[2]常军，南文虎，李玉明.基于蒙特卡洛法的DELTA机器人工作空间分析[J].机械工程师，2012（09）：14-15.